Distributed Matching Theory-Based Task Re-Allocating for Heterogeneous Multi-UAV Edge Computing

Yangang Wang ,Xianglin Wei ,Hai Wang ,Yongyang Hu ,Kuang Zhao ,Jianhua Fan

1 College of Communications Engineering,Army Engineering University of PLA,Nanjing 210007,China

2 The Sixty-Third Research Institute,National University of Defense Technology,Nanjing 210007,China

Abstract: Many efforts have been devoted to efficient task scheduling in Multi-Unmanned Aerial Vehicle (UAV) edge computing.However,the heterogeneity of UAV computation resource,and the task re-allocating between UAVs have not been fully considered yet.Moreover,most existing works neglect the fact that a task can only be executed on the UAV equipped with its desired service function(SF).In this backdrop,this paper formulates the task scheduling problem as a multi-objective task scheduling problem,which aims at maximizing the task execution success ratio while minimizing the average weighted sum of all tasks’ completion time and energy consumption.Optimizing three coupled goals in a realtime manner with the dynamic arrival of tasks hinders us from adopting existing methods,like machine learning-based solutions that require a long training time and tremendous pre-knowledge about the task arrival process,or heuristic-based ones that usually incur a long decision-making time.To tackle this problem in a distributed manner,we establish a matching theory framework,in which three conflicting goals are treated as the preferences of tasks,SFs and UAVs.Then,a Distributed Matching Theory-based Re-allocating(DiMaToRe) algorithm is put forward.We formally proved that a stable matching can be achieved by our proposal.Extensive simulation results show that DiMaToRe algorithm outperforms benchmark algorithms under diverse parameter settings and has good robustness.

Keywords: edge computing;heterogeneity;matching theory;service function;unmanned aerial vehicle

I.INTRODUCTION

Unmanned Aerial Vehicle (UAV)-empowered computing is a promising computation paradigm to serve mobile devices (MDs) in infrastructure-less areas,such as a disaster emergency response[1–6].An MD can offload computation-intensive or time-sensitive tasks to the UAV,which will execute the received tasks on their desired service functions (SFs) utilizing virtualization technique [7–9] (SF matchingfor short in the following analysis).Typically,multiple UAVs compose a UAV swarm to process the offloaded tasks from a large number of MDs since one single UAV only has limited resources,energy supply and coverage range.In order to efficiently utilize the limited UAV computation resources,some task scheduling methods have been proposed,mainly including heuristic-based [10–20] and machine learning-based methods [21–28].Heuristic-based methods typically treat the task scheduling problem as a bin-packing problem,and derive a solution using an iteration process.This process usually incurs a long decisionmaking time.In contrast,machine learning-based methods can greatly shorten the decision-making time in dynamic scenario with the cost of a long training time and high computation complexity.Most of them are developed under the condition that the positions of MDs and the attributes of tasks are known in advance.However,in the emergency response scenario [3,4]considered in our paper,the UAV swarm knows nothing about MDs and tasks before their deployment.Under this circumstance,an even UAV deployment has the best potential to ensure a large coverage area for accepting the offloaded tasks [29].To promote the service performance with an even UAV deployment,this paper focus on how to conduct the re-allocation of the tasks in a real-time distributed manner among the heterogeneous UAVs without prior knowledge about MDs.In the heterogeneous scenario,different UAVs have different computation and peripheral resources,and host different SF instances.From the perspective of the UAV swarm,it wants to maximize task execution success ratio while minimizing the energy consumption;in contrast,the MDs want to minimize the completion time of the offloaded tasks.The coupled goals pose a great challenge in achieving their best tradeoff through efficient resource scheduling of the UAV swarm.This could easily fail existing task scheduling algorithms developed in homogeneous settings[10–28].In this backdrop,this paper formulates the task scheduling problem as a multi-objective task scheduling problem.The formulated problem aims at maximizing the task execution success ratio while minimizing the average weighted sum of all tasks’completion time and energy consumption.Due to the lack of a central entity in a self-organized UAV swarm,it is impractical to solve this problem in a centralized way utilizing the traditional multi-objective optimization algorithms [30][31].Moreover,collecting the global resource provision and request information and making scheduling decision will incur an intolerable delay for a resource-limited UAV.Thus,a lowcomplex distributed solution is preferred.

To tackle this problem,we establish a matching theory framework,in which three coupled goals are treated as the preferences of tasks,SFs and UAVs.Then,a Distributed Matching Theory-based Re-allocating(DiMaToRe)algorithm is put forward to coordinate the three-sided matching process between tasks,SFs and UAVs.The contributions in this paper are shown as follows:

1.A multi-objective optimization problem is built for the task scheduling problem to jointly optimize three coupled objectives,including the task execution success ratio,the task completion time,and the UAV energy consumption.To solve this problem,a distributed three-sided matching framework is established,in which three coupled goals are treated as the preferences of tasks,SFs and UAVs;

2.A Distributed Matching Theory-based Reallocating (DiMaToRe) algorithm is put forward under the three-sided matching framework.DiMaToRe algorithm is formally proved to converge to a stable matching that can simultaneously optimize three coupled goals after a finite number of iterations.

3.To address the challenges brought by the dynamic arrival tasks with unpredictable resource requirements,a time slot partitioning protocol is designed.The service period is divided into successive time slots with equal length.A mini-slot is reserved for the UAVs to share their computation resources status.In each time slot,the tasks arrived in the previous time slot can be re-allocated between UAVs through DiMaToRe algorithm;

4.To cope with the challenge brought by unstable aerial links,the link stability detection mechanism is designed and embedded in DiMaToRe.It ensures that each UAV only re-allocates tasks to those neighbors with stable aerial links,which promotes the robustness of our proposal when facing aerial link failures.

5.A series of simulations are conducted to evaluate the proposal.The task execution success ratio of DiMaToRe algorithm is roughly 10%higher than benchmark algorithms.On the other hand,the average weighted sum of the task completion time and energy consumption of DiMaToRe algorithm is roughly 50% lower than of the benchmark algorithms before the UAV swarm enters the saturation state.Lastly,although unstable aerial links may slightly reduce the average execution success ratio of tasks,DiMaToRe can still work stably without remarkable performance degradation,showing good robustness.

The remaining of this paper is organized as follows.Section II summarizes related work.The model and problem formulation of the proposed system are introduced in Section III.Section IV describes the details of our proposed DiMaToRe algorithm.The experiments and analysis of the results are presented in Section V.Finally,Section VI concludes this paper.

II.RELATED WORK

In a multi-UAV edge computing system,multiple types of variables (e.g.,task offloading decisions,computing resource allocation,UAVs trajectories,power allocation)need to be jointly optimized for the desired optimization objective.Existing efforts can be roughly divided into two categories: heuristic-based methods and machine learning-based ones.

2.1 Heuristic-Based Methods

Xiao et al.[10]focused on the scenario in which multiple heterogeneous UAVs process missions cooperatively,and presented an efficient routing and task allocation algorithm based on ant colony system for minimizing energy consumption.Wang et al.[11] designed a dynamic pricing scheme under complete and incomplete information,then optimized the energy allocation.Cheng et al.[12] formulated an energy consumption and task execution delay minimization as a multi-objective optimization problem,and solved it based on the task assignment,Differential Evolution (DE)-aided and non-dominated sort steps.Considering the priority constraints among sensors,Sun et al.[13]proposed a learning-based cooperative particle swarm optimization algorithm to minimize the maximum response time of forest fire monitoring.Due to the complexity of the multi-UAV edge computing system,most optimization problems need to be solved via jointly optimizing user association,power control,computing power allocation,location planning,task scheduling,etc.Most optimization models are nonconvex.The alternating iteration method is one of the most popular approaches for solving non-convex optimization problems.References [14–18] divided the original complex problem into several simplified subproblems,which were solved through typical convex optimization or heuristic algorithms.A final solution to the original problem was obtained through iterating the sub-problems.Methods based on game theory were also adopted for solving optimization problems.[19,20]considered UAVs as individual players with private interests,then optimized their energy consumption and task processing delay.The optimization problem was finally formulated as an offloading game with at least one Nash equilibrium.

2.2 Machine Learning-Based Methods

Machine learning techniques had been widely adopted for task scheduling and resource allocating due to their unique capability.Chang et al.[21]jointly optimized the quality of service and path planning through reinforcement learning methods based on the terminal users’ demand,risk and geometric distance.Seid et al.[22]designed a deep deterministic policy gradientbased collaborative tasks offloading and resource allocation framework for minimizing task execution energy consumption and delay.Liu et al.[23]proposed a two-phase Deep Reinforcement Learning (DRL)-based task offloading algorithm.Ren et al.[24] proposed a real-time scheduling approach for large-scale UAV-assisted mobile edge computing based on a deep reinforcement learning.[25,26]separately solved the response time minimization and the task load fairness problem through the multi-agent reinforcement learning algorithm.Yang et al.[27] proposed a loadbalance-oriented UAV deployment scheme and a task scheduling algorithm based on the DRL.Yang et al.[28] proposed a hierarchical machine learning tasks distribution framework for the Deep Learning (DL)-based visual target tracking system to minimize the weighted-sum cost with the inference error rate constraint.

Table 1 provides a comprehensive comparison between our work and existing efforts from different perspectives.To our best knowledge,this is the first paper that study the problem of SF matching and the task re-allocating in heterogeneous UAVs without prior knowledge of MDs.

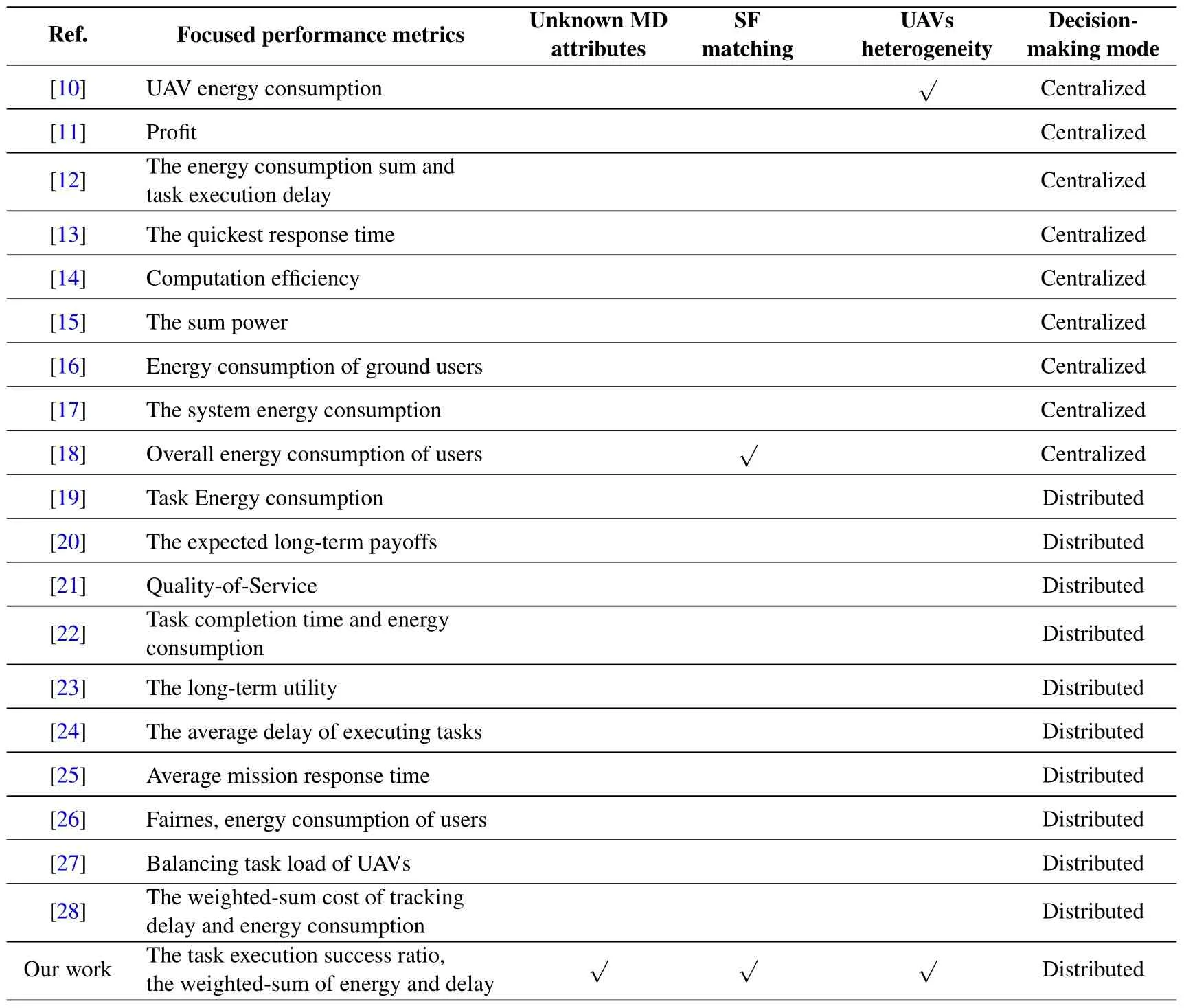
Table 1. Comparison between this work and related ones.“√” indicates the corresponding problem is considered,“×”indicates the corresponding problem is neglected.

III.SYSTEM MODEL AND PROBLEM FORMULATION

3.1 Distributed Cooperative Architecture

As shown in Figure 1,multiple rotary-wing UAVs with heterogeneous computation resources compose an edge computing network,which evenly hover overthe mission area and operate in a distributed manner.For the simplicity of description,the “heterogeneous Multi-UAV edge computing network” and“rotary-wing UAV” will be referred to as “UAV swarm” and “UAV” for short in the rest of this paper,respectively.Denote the set of UAVs as U={u1,u2,...,un,...,uN}.These UAVs are flying at a constant altitude H,and the location of uncan be represented by (xn,yn,H).As shown in Figure 2,the computing resource of each UAV includes CPU cores,peripherals and internal buses.Each peripheral has several ports,each of which can connect to a CPU core and provide auxiliary functions for it.The connection and release between the CPU cores and the peripheral ports can be made by configuring the internal bus[32].Moreover,each UAV deploys several SFs according to its own computation resources.SFs provide the computing service for a requesting task by creating a service instance.A task can only be executed by a service instance of its matching SF.

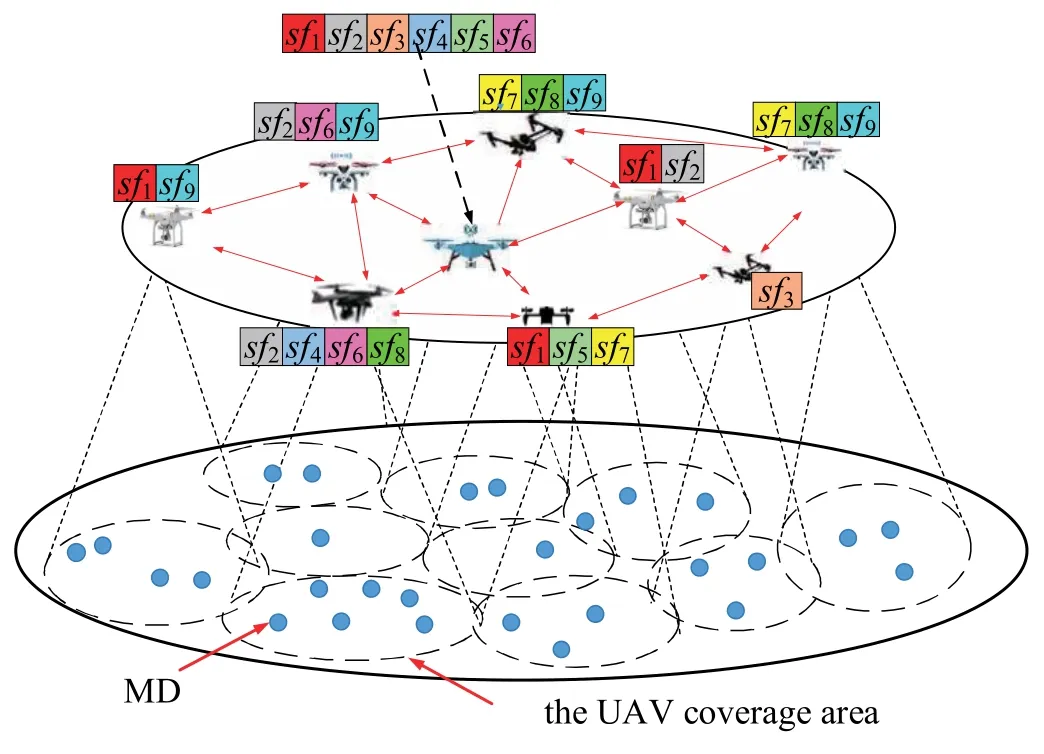
Figure 1. A heterogeneous Multi-UAV edge computing scenario.Each MD on the ground can offload tasks to its nearest UAV that hosts SFs.Tasks can be re-allocated among UAVs for optimal task execution.

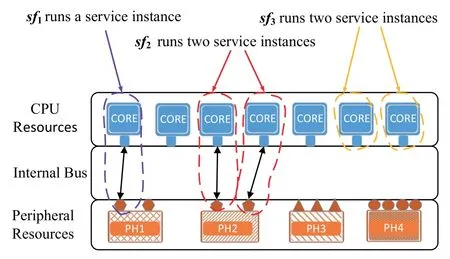
Figure 2. An illustration of the resources and SFs hosted by a UAV.Three SFs,i.e.,sf1,sf2,and sf3 are deployed on the UAV.sf2 starts two service instances,and each of them occupies one CPU core and a port from PH2(a peripheral on the UAV).In contrast,a service instance of sf3 only consumes one CPU core.

SFs consume computation resources when creating instances.Generally,the computation resources consumed by different SFs are different [33,34].The SFs considered in this paper are divided into two categories: one is that its service instances only occupy CPU cores;the other is that its service instances not only occupy CPU cores but also peripheral ports.From the perspective of information security,this paper stipulates that each SF instance independently occupies a single CPU core or a single peripheral port during its operation.As shown in Figure 2,sf2starts two service instances,and each service instance occupies one CPU core and one port of peripheral PH2;sf3starts two service instances,and each service instance occupies one CPU core.Moreover,due to the heterogeneity of UAVs,the set of SFs deployed on each UAV may be different;and the performance of the same SF deployed on different UAVs is also differ-ent.When a UAV receives a task from an MD,it may not be the best alternative to execute this task.To efficiently utilize the computation resources,when UAVs receive tasks from MDs,they should collaborate with each other to re-allocate those tasks to the best matching UAVs for execution.For the ease of description,the main notations used in this paper are listed in Table 2.

Table 2. Notations.

3.2 Communications Model

Orthogonal frequency division multiplexing (OFDM)is adopted as the transmission technique between UAVs.Assume that there are enough number of subchannels in the OFDM system.The bandwidth of each sub-channel is B0,and each sub-channel can transmit data without conflict.Furthermore,a sub-channel is chosen as the control channel for coordination between UAVs;all other sub-channels are chosen as the data channel for transmitting tasks between UAVs.In the control channel,as shown in Figure 3,a time slot partition protocol is designed here to regulate the interaction between UAVs.The serving period is divided into successive time slots with equal length.Each time slot is a basic unit for task scheduling.At the beginning of each time slot,a mini-slot is reserved for all UAVs to synchronize their current available SFs.The available SF refers to the one that can continue to create service instances for tasks.The SF becomes unavailable when it can not create service instances due to insufficient computing resources.For tasks offloaded to UAVs in the (n −1)-th time slot,UAVs must complete their re-allocating decisions in the n-th time slot.An example of interaction between UAVs is shown in Figure 3.In time slot#0,some MDs offload a different number of tasks to u1,u2and u3,respectively.At the beginning of time slot#1,the available SF sets deployed on u1,u2,and u3are{sf6,sf4,sf7},{sf8,sf3,sf1} and {sf8,sf7,sf4},respectively.In the mini-slot of time slot#1,each UAV broadcasts its available SF set information to its neighbors.After the mini-slot,each UAV can obtain the available SFs set deployed on itself and its surrounding.Then,each UAV selects a preferred SF for each of its tasks by interacting with other UAVs.Finally,these tasks will be transmitted to their preferred SFs through data channels.Similarly,in time slot #2,each UAV selects a preferred SF from the available SFs set deployed on itself and its surrounding for each task offloaded in time slot#1.

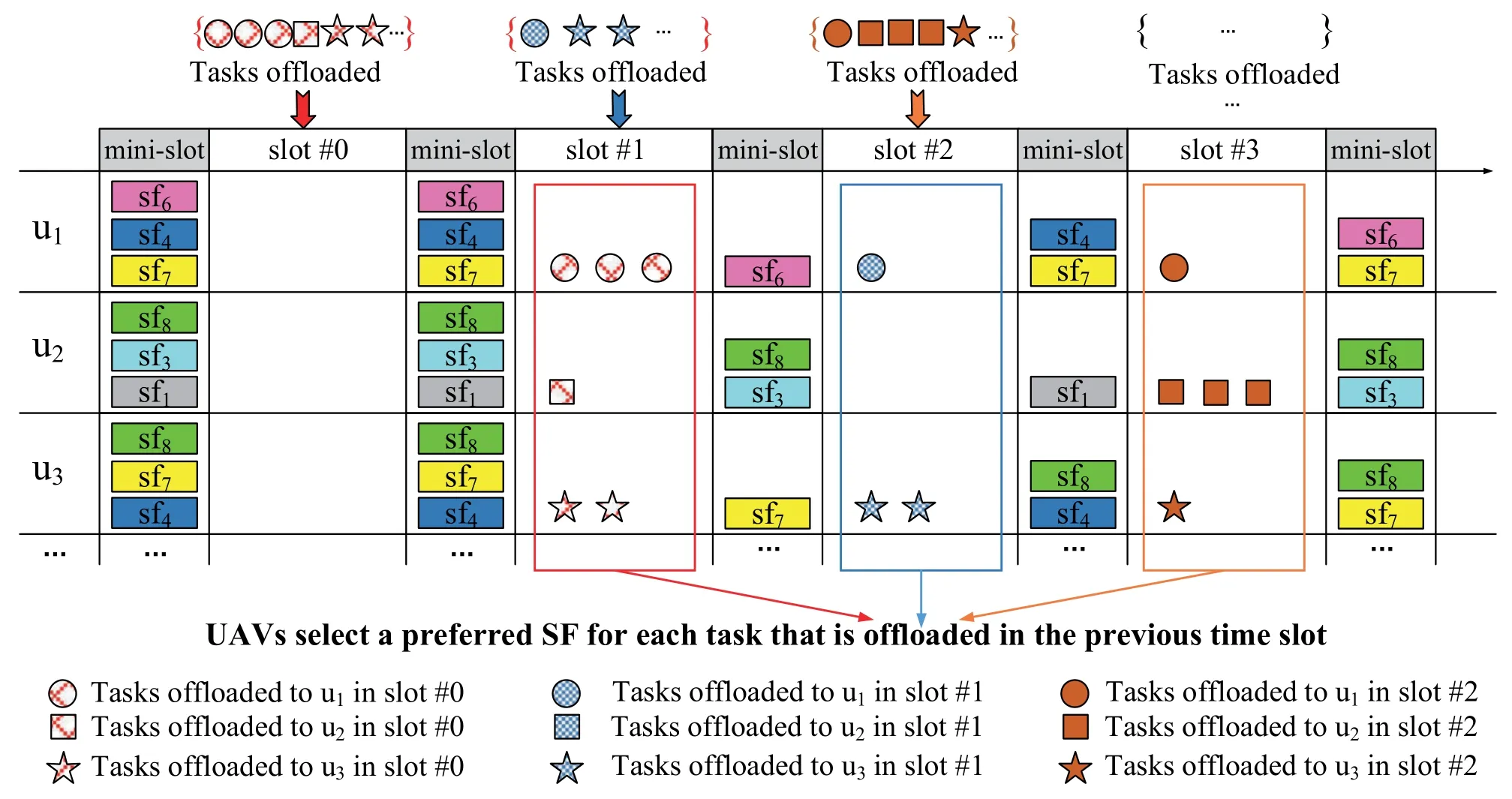
Figure 3. The time slot partitioning protocol.

Assume that the channel is a free space attenuation model[35].Then,the data transmission rate rn,mfrom unto umbased on a sub-channel can be expressed as:

where β0is the transmit power gain at a reference distance of 1 meter.ρ2is the noise power.Pnis the transmission power of un.dn,mis the distance between unand um.

3.3 Service Model

where pm,qrepresents the function type of sfm,q.fm,qrepresents the performance of sfm,qand is equivalent to the frequency of CPU core occupied by its service instance[24].is the maximum number of service instances that can be simultaneously started by sfm,qon um,that is,the maximum number of tasks that sfm,qcan simultaneously execute.As shown in Figure 2,the maximum number of service instances simultaneously started by sf2is 2,which is determined by the number of ports of peripheral PH2;the maximum number of service instances simultaneously started by sf3is 7,which is determined by the number of CPU cores.As can be seen from the above description,any type of service instance occupies one CPU core.Thus,the maximum total number of service instances that can be started simultaneously on each UAV is equal to the number of CPU cores.Defineand nm,qto represent the number of CPU cores on umand the number of tasks currently being executed on sfm,q,respectively.Then,the following constraints should be satisfied.

Eq.(3)shows that the number of tasks currently being executed on sfm,qdoes not exceed its capacity constraints.Eq.(4) means that the total number of tasks currently being executed on umdoes not exceed the limit of CPU resources.

3.4 Task Model

Assume that unreceives jntasks offloaded from MDs in a time slot,denoted as a set Tn=.Task tn,jis modeled as follows:

3.4.1 Task Completion Time

Task completion time is mainly generated by reallocating and executing tasks.The re-allocating time is the time consumed for transmitting tasks between UAVs.We define the re-allocating time of tn,jto sfm,qas:

where n=m means that tn,jand sfm,qare on the same UAV.

The execution time is the consumed time for executing a task on its desired SF.We define the execution time of tn,jexecuted on sfm,qas.

Therefore,the task completion time of tn,jexecuted on sfm,qcan be expressed as follows:

3.4.2 Energy Consumption

Energy consumption is mainly generated by reallocating and executing tasks.Re-allocating consumption is the consumed energy for transmitting tasks between UAVs.We define the re-allocating consumption of tn,jre-allocated to sfm,qas:

where n=m means that tn,jand sfm,qare on the same UAV.Execution consumption is the consumed energy for executing a task on its desired SF.We define the energy consumption of tn,jexecuted on sfm,qas[24]:

where λmis the effective switching capacitance of um.

Therefore,the task energy consumption of tn,jexecuted on sfm,qcan be expressed as follows:

3.5 Problem Formulation

For a task,there may be multiple UAVs that can satisfy its computing requirement.It wants to be executed on the UAV that can minimizes its completion time.On the other hand,each UAV may receive requests from a number of tasks,and it can not execute all tasks due to resource limitation.The UAV swarm prefers to execute as many tasks as it can with the least energy consumption.Therefore,the task scheduling process is to find the optimal matching between tasks and UAVs(SFs).A binary decision variableis defined to represent the matching results between tasks,UAVs and SFs,as follows:

For UAV swarm,the more tasks that can be successfully executed,the better.Therefore,the optimization goal is to maximize the task execution success ratio,which is defined as:

For a task,the shorter its completion time,the better;for UAV swarm,the less energy it consumes,the better.To compromise the task completion time and energy consumption,another optimization goal in this paper is to minimize the average Weighted sum of Completion time and Energy consumption(WeCE)per task bit,which is formulated as:

According to Eq.(13) and Eq.(14),a multiobjective optimization problem can be formulated as:

Constraint (C1) specifies the valid ranges of the involved variables in Constraint(C2)～Constraint(C6);Constraint (C2) is the binary re-allocating constraint;Constraint(C3)means that each task only is executed on one SF or is not executed;Constraint(C4)ensures that the number of tasks executed on each SF does not exceed its capacity constraints;Constraint(C5)restricts that the total number of tasks executed on each UAV does not exceed its capacity constraints;Constraint(C6)ensures that the task completion time does not exceed its tolerable delay.

IV.DISTRIBUTED MATCHING THEORYBASED TASK RE-ALLOCATING

In P1,minimizing-F1is a 0-1 linear integer programming problem and equivalent to maximizing F1,and minimizing F2is a 0-1 nonlinear integer programming problem.At the same time,there is a close coupled relationship between F1and F2.Therefore,P1is a nonconvex nonlinear optimization problem,which can not be efficiently solved in large-scale scenarios.To solve P1,we treat it as a three-sided matching problem between tasks,SFs,and UAVs.

4.1 Three-Sided Matching Framework

The Student-Project Allocation(SPA)[36]is the classical three-sided matching framework.The SPA problem involves a set of students,projects,and lecturers.Each project is offered by a specific lecturer,and both lecturers and projects have capacity constraints (i.e.,a maximum number of students that each project and each lecturer can accept,respectively).Typically,a lecturer can provide a series of projects,and a student also have multiple optional projects.Furthermore,each student has preferences over the projects that are acceptable,while each lecturer has preferences over the acceptable students.Based on the preferences of students and lecturers,the goal is to find a stable matching that pairs students to projects offered by each lecturer,while satisfying the capacity constraints and taking into account the interests both students and teachers.In an analogous manner,our goal is to reallocate tasks (students) to acceptable SFs (projects)deployed on UAVs(lecturers),while satisfying the capacity constraints of SFs and UAVs.Inspired by the SPA framework,we can model P1as a three-sided matching problem between tasks,SFs and UAVs.In order to obtain an approximate optimal solution of P1,the preferences defined for the three sides are the key,which must be able to balance the interests of tasks and UAVs.To that end,a few definitions proposed in this paper must first be given.

Definition 1.(Acceptability)sfm,qis acceptable for tn,jwhen 1)the value of pm,qis equal to the value ofand 2) the task completion time of tn,jexecuted on sfm,qis not bigger than the tolerable delay dn,j.Define the set of acceptable SFs for task tn,jas An,j.

Definition 2.(Task preference and Task preference list)When the WeCE of tn,jexecuted on one acceptable sfm,qis less than that of tn,jexecuted on the other acceptable,tn,jprefers sfm,qto.tn,jhas a preference list,which ranks An,jin a descending order from the most preferred to the least preferred.Letdenote the preference list of tn,j,whererefers to the most(least)preferred SF.

Definition 3.(UAV preference and UAV preference list)A UAV first provides computation service for its most preferred task when simultaneously facing the requests from multiple tasks.Let={t(1),t(2),...,t(x)} denote the preference list of um,where t(1)(t(x)) is its most (least) preferred task.A preference order is designed for umas follows:

1.The most preferred task by umis the task that has only one acceptable SF,which is beneficial to maximizing F1.When facing multiple tasks only one acceptable SF,umprefers the task with the smaller WeCE executed on it,which is beneficial to minimizing F2.

2.The secondary preferred task by umis the task that has more than one acceptable SFs.When facing multiple secondary preferred tasks,umprefers the task with the larger difference of WeCE separately executed on its most preferred SF and on its secondary preferred SF.This can effectively reduces the sum of all tasks’ WeCE (the proof is presented in Appendix A),thus favoring the minimization of F2.When facing multiple tasks with the same WeCE differences,umprefers the task with the smaller WeCE executed on it.

Definition 4.(SF preference and SF preference list)Denoteas the preference list of sfm,q,and stipulate that sfm,qand umhave the same preference order.Then,can be obtained fromby deleting those tasks that consider sfm,qto be unacceptable.In this way,the ranking ofis inherited from.

Definition 5.(Capacity constraint)As mentioned above,um∈U has a capacity constraint,which is the maximum number of tasks that can be executed on umsimultaneously.Furthermore,each sfm,q∈SFmhas a capacity constraint,which is the maximum number of tasks that can be executed on sfm,qsimultaneously.umis said to be under-subscribed,full,or over-subscribed if the number of tasks that it has accepted is less than,equal to,or greater than.A sfm,qis said to be under-subscribed,full,or over-subscribed if the number of tasks that it has accepted is less than,equal to,or greater than.

Definition 6.(Matching)A matching M is defined as a subset of T × SF,T=,SF=SFm.For any task tn,j,if a pair(tn,j,sfm,q)∈M,we say that tn,jis assigned to sfm,q.A matching M is a set of feasible pairs between tasks and SFs,which satisfies the following conditions[36]:

1.(tn,j,sfm,q)∈M implies that sfm,q∈An,j(i.e.,sfm,qmust be acceptable for tn,j);

2.tn,jis assigned to at most one SF (i.e.,,in other words,tn,jcan only be executed on one SF;

3.For each sfm,q∈SF,its capacity constraint must be satisfied,;

4.For each um∈U,its capacity constraint must be satisfied,.

For the convenience of description,M(tn,j)=sfm,qindicates that tn,jis assigned to sfm,qin M,whereas M(sfm,q)is the set of tasks that are assigned to sfm,qand M(um) is the set of tasks that are assigned to um.

Definition 7.(Blocking)A blocking pair(tn,j,sfm,q)∈(T×SF)M can block a matching M to be stable,which satisfies the following conditions[36]:

1.sfm,q∈An,j(i.e.,tn,jfinds that sfm,qis acceptable);

2.Either tn,jis unassigned in M (i.e.M(tn,j)=NULL),or tn,jprefers sfm,qto M(tn,j);

3.Either

a) sfm,qis under-subscribed and umis undersubscribed,or

b) sfm,qis under-subscribed,umis full,and umprefers tn,jto the least-perferred task in M(um),or

c) sfm,qis full and prefers tn,jto the leastperferred task in M(sfm,q).

Definition 8.(Stable matching)A matching M is considered stable if M has no blocking pairs[36].In a stable matching M,all tasks will simultaneously obtain best-possible SFs.

4.2 Algorithm Design

Although David et al.[36] proposed an optimal algorithm for the SPA problem,it is difficult to solve P1 by directly utilizing it.This is because that it not only needs to run on a central node,but also requires the complete set of participants (i.e.,tasks,SFs,and UAVs) and their preference lists as its input parameters.In the distributed scenario considered in this paper,the distribution and task attributes of MDs are unknown in advance,so that the required complete preference lists are difficult to be built.Therefore,a distributed DiMaToRe algorithm is put forward under the above three-sided matching framework,as shown in Figure 4,which includes four modules: 1) available SFs notification module,2) re-allocating request module,3)SFs response module,and 4)task transmitting module.The DiMaToRe algorithm is deployed on each UAV,and is repeatedly executed in each time slot to solve the newly formed P1.

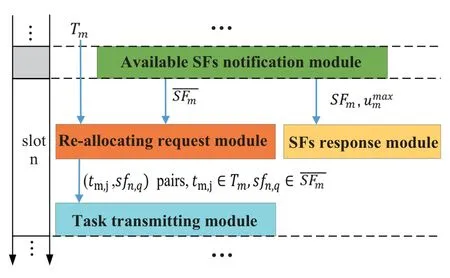
Figure 4. Work flow chart of modules in DiMaToRe algorithm.

A workflow of DiMaToRe on UAV umis shown as Figure 4,which makes decisions for tasks,denoted as the set Tm,that arrive in the previous time slot.In the mini-slot,umcan get its available SFs on itself and its surrounding,denoted as,through available SFs notification module.Then,re-allocating request module requests the preferred SF for each task according to the set.At the same time,SFs response module replies to the request to SFmfrom other UAVs.At the end of the time slot,task transmitting module transmits tasks to their preferred SFs according to the matching pairs output by re-allocating request module.

4.2.1 Available SFs Notification Module

Alg.1 illustrates the working process of the available SFs notification module deployed on um.In each mini-slot,available SFs notification module refreshes the values ofaccording to its idle computation resources (in Step#1).Then,this module broadcasts the available SFs in SFmto its neighbor UAVs.At the same time,umalso receives the broadcast messages from its neighbor UAVs.The instability of the aerial link between UAVs is unavoidable.In order to ensure the robustness of Di-MaToRe algorithm,when the UAV conducts task reallocation,its neighbor UAVs that have unstable links with it can not be included.If the link between a UAV and its neighbor is considered to be stable,this neighbor is classified as its candidate UAVs that can provide available computation resources for task re-allocating.For this reason,a link detection mechanism is added to the available SFs notification module for selecting candidate UAVs,as shown Alg.2.If a UAV can continuously receive Nlthe notification messages from a neighbor UAV,this neighbor UAV is regarded as its candidate UAV (in Step #3～#13 of Alg.2).At the end of the mini-slot,umobtains the set,which includes the available SFs deployed on itself and its candidate neighbor UAVs(in Step#2～#9 of Alg.1).

4.2.2 Re-Allocating Request Module

Alg.3 illustrates the working process of the reallocating request module on um.Re-allocating request module firstly builds a task preference list for tm,j∈Tmbased on,Def.1 and Def.2.Then,it constructs a provisional feasible pair (tm,j,sfn,q) for each tm,j∈Tm,and sends a request message to sfn,q(in Step #3～#15).If sfn,qis deployed on um(i.e.,n=m),the request message is directly sent to the its SFs response module;otherwise,the request message is sent out through the control channel.When re-allocating request module receives a response message indicating that the request of tm,jis rejected,it will refresh the preference list of tm,j,re-construct a provisional feasible pair for this task,and re-send the request message (in Step #17～#21).At the end of the time slot,all provisional feasible pairs become the final pairings between tasks and SFs (in Step #23～#29),which are the solution of problem P1.

The number of tasks arriving at umis|Tm|in each time slot,and the maximum length of each task’s preference list is |U|.Therefore,re-allocating request module on umsends at most |Tm|.|U| request messages to other UAVs,which has the polynomial-time complexity of O(|Tm|.|U|).

4.2.3 SFs Response Module

Alg.4 illustrates the working process of the SFs response module on um.In the distributed manner,UAVs can not obtain its preference list in advance,and can only dynamically improve its preference list as the requests of tasks arrive.At the end of the mini-slot,SFs response module separately builds empty preference lists for umand the available SFs in SFm.Then,it waits for the request messages arriving and dynamically improves these preference lists.When a request message arrives,SFs response module evaluates the preference to the requesting task based on the preference order in Def.3.Next,the requesting task is separately inserted into the preference list of umand the requested SF (in Step #3～#5).Lastly,this module checks whether there is any constraint violation in the preference lists,i.e.whether the number of tasks exceeds the capacity constraint.If so,the least preferred task will be removed from the list;otherwise,no action is needed(in Step#6～#13).

4.2.4 Task Transmitting Module

At the end of a time slot,(tm,j,sfn,q) final pairs are output by the re-allocating request module.The task tm,jwith nm and its sfn,qNull will be transmitted to sfn,qthrough the data channel.

4.3 Algorithm Convergence Analysis

Lemma 1.DiMaToRe algorithm converges to a stable matching solution by a finite number of iterations.

Proof.According to Def.6,a matching M can be constructed after conducting DiMaToRe algorithm.Moreover,according to Def.8,a matching M is stable if M has no blocking pairs.Next,we prove that the derived matching M by DiMaToRe has no blocking pairs.

According to Condition 1 in Def.7,if M has a blocking pair(tm,j,sfn,q),sfn,qmust be acceptable for tm,j.Therefore,blocking pairs of M can only appear in the deleted provisional feasible pairs(in Step#18 of Alg.3)or the un-assigned pairs.A task’s un-assigned pairs can be obtained at the end of scheduling time slot(i.e.after Step#22 in Alg.3),which are denoted as the pairs (tm,j,sf),sf ∈sfn,q.Suppose the pair(tm,j,)is a deleted provisional feasible pair and the pair(tm,j,)is an un-assigned pair.Next,we respectively prove that the above two kinds of pairs do not belong to the blocking pair of M.

1.In the Step #17 and #18 in Alg.3,if the provisional feasible pair (tm,j,) is deleted,that is,task tm,jis rejected by.The reason includes: (i)is full and prefers the leastperferred task into task tm,j;(ii) oris under-subscribed,is full and prefers the least-perferred task into tm,j.Then,the provisional deleted pair(tm,j,)fails a),b)and c)of Condition 3 in Def.7,so that it is not blocking pair of M;

2.After Step#22 in Alg.3,if task tm,jis finally accepted by sfn,q(i.e.,M(tm,j)=sfn,q),tm,jmust prefer sfn,qto.Then,the un-assigned pair(tm,j,)fails Condition 2 in Def.7.If task tm,jis not accepted by any SF(i.e.,M(tm,j)=NULL),the preference listmust be empty and has no the remaining preferred SF.Then,unassigned pair(tm,j,)will not exist.Therefore,un-assigned pair (tm,j,) is not a blocking pair.

Since the maximum length of the task preference list is |U|,which is the total number of UAVs.The number of tasks arriving at umfrom the MDs is|Tm|in each time slot.Therefore,both |U| and |Tm| are limited,then DiMaToRe algorithm can converge to a stable matching solution in a limited number of iterations.

V.SIMULATION AND RESULTS ANALYSIS

5.1 Experimental Settings

N UAVs evenly spread in a 10km×10km area.The number of CPU cores and SFs depolyed on each UAV is randomly set in a certain range.Each UAV randomly receives the tasks offloaded from MDs.The total number of tasks offloaded to the UAV swarm ranges from 600 to 2000,which investigates the system performance from light to heavy load.To show the impact of WeCE’s magnitude difference on F2,α is chosen from {0.01,0.1,1}.For each scenario,the simulation is repeated 100 times,and the final simulation results are their average.The main parameter settings are included in Table 3.

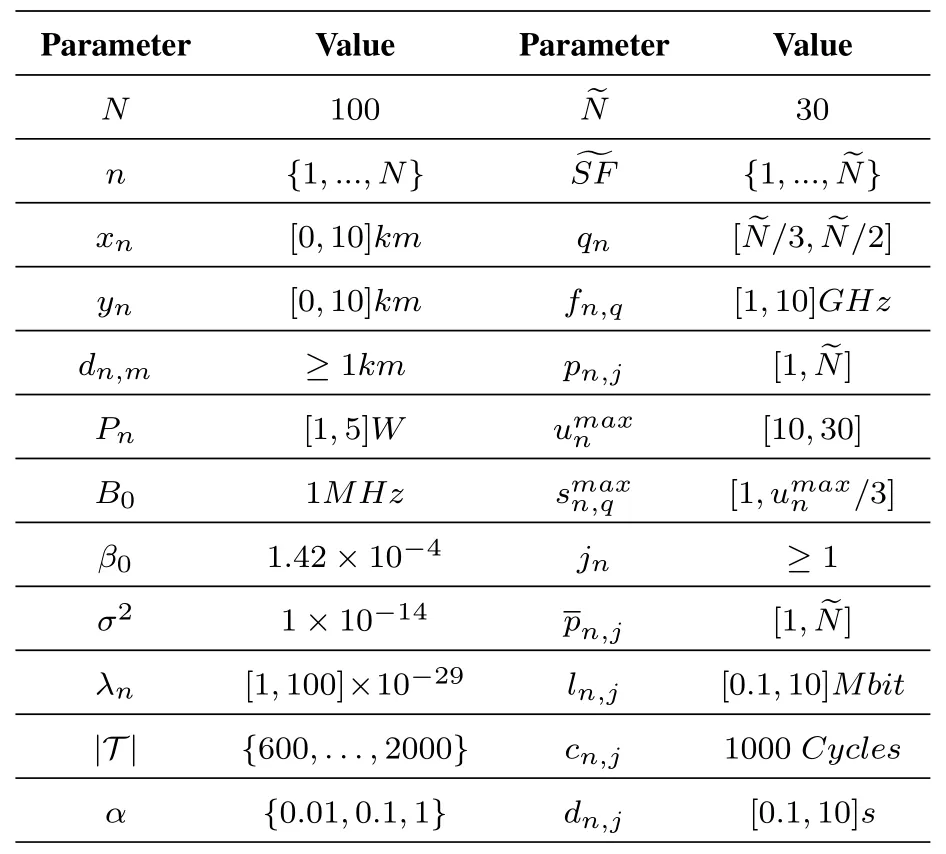
Table 3. Parameter settings.

Comparison Benchmarks.Four algorithms are chosen as comparison benchmarks: No Reallocating (NoRe),Random Re-allocating (RanRe),Nearest-distance Greedy Re-allocating (NeGRe),and Minimum Weighted-sum Greedy Re-allocating(MiWeGRe).In NoRe algorithm,when a UAV receives tasks from the ground,it directly executes tasks locally without re-allocating.In RanRe algorithm,a UAV randomly selects an SF for each task from its preference list.If the request is rejected,the UAV will continue this random selection process from the remaining SFs until the request is accepted or no SF is available.The latter two algorithms,i.e.,NeGRe and MiWeGRe,are developed based on greedy algorithms inspired by references[17]and[37].In NeGRe algorithm,the UAV always select the nearest SF in the task preference list.In MiWeGRe algorithm,the UAV always selects the SF with the minimum WeCE in the task preference list.

Comparison Metrics.The following performance metrics are adopted:

1.Average task execution success ratio: it is the value of function F1,and is adopted to reflect the feasibility of algorithms;

2.Average WeCE ratio: an algorithm’s average WeCE ratio is defined as the ratio of its F2value and MiWeGRe algorithm’s F2value.Therefore,MiWeGRe algorithm’s average WeCE ratio is always 1.The lower an algorithm’s average WeCE ratio,the better its performance.

3.Average satisfaction degree ratio: it is used to reflect whether a task is more likely to be matched with its high-preferred SF among multiple choices.The satisfaction degree of task tn,jis defined as:

where hm,qrepresents the position order of sfm,qin the initial preference list.If sfm,qis the most (least) preferred SF of tn,j,hm,qis 1.In order to reflect the performance of different algorithms in terms of task satisfaction degree,this paper selects MiWeGRe algorithm as a comparison benchmark.Given the satisfaction degreeof task tn,jin MiWeGRe algorithm,the average satisfaction degree ratio of the evaluated algorithm is defined as:

In this way,the larger the number of tasks with a higher satisfaction degree,the higher this algorithm’s satisfaction degree ratio.Note that MiWe-GRe algorithm’s average satisfaction degree ratio is always 1.

4.Average requesting times:it is the average number of requests initiated by a task before it finally obtains an acceptable SF or fails.

5.2 Experimental Results and Analysis

We firstly generate a simulation environment based on the parameters in Table 3.The weighting coefficient α in the problem P1can obviously affect the value of WeCE,which can change the ranking order in the preference list of tasks,UAVs and SFs,and ultimately affect the re-allocating decision and optimization result.Therefore,We make simulation experiments based on three different α values.

5.2.1 Analysis of the Average Task Execution Success Ratio

Figure 5 shows the average task execution success ratio of algorithms under different α.The result shows that DiMaToRe algorithm has the highest success ratio,especially with the gradual increase of tasks,it can still maintain a high success ratio.This is mainly because that the task with only one acceptable SF is the most preferred by UAVs and can obtain priority services in DiMaToRe algorithm.In addition,we can see that the average task execution success ratio of NoRe algorithm is the lowest and is unbearable,which fully reflects the necessity of re-allocating.Finally,we can also see that different weighting coefficients have little effect on the average task execution success ratio.This is mainly because that the weighting coefficients can only affect the WeCE value,which has no obvious correlation with the task execution success ratio in all algorithms.

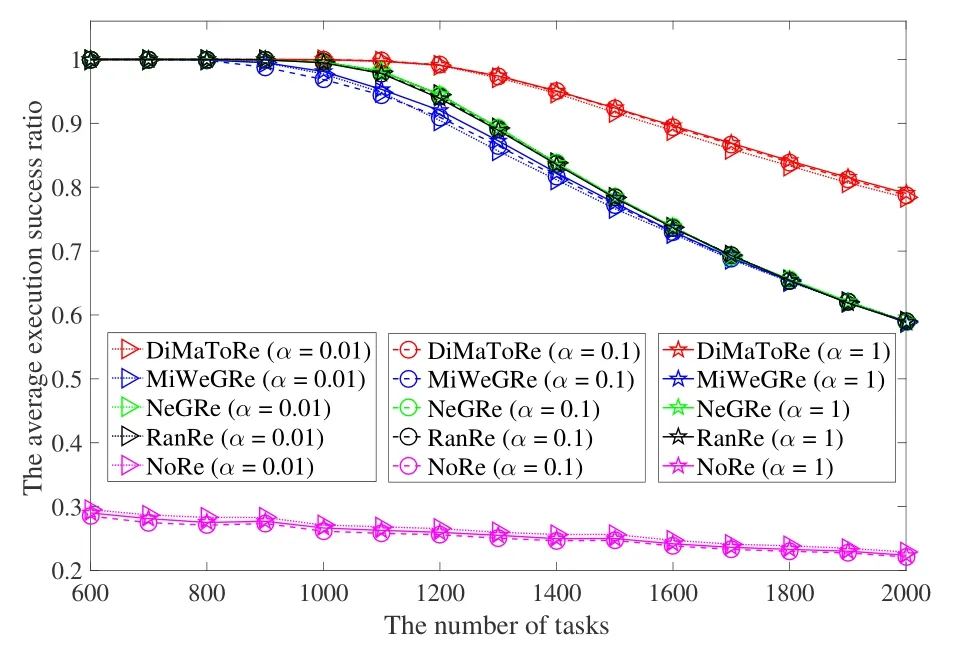
Figure 5. The average task execution success ratio under different α.

5.2.2 Analysis of the Average WeCE Ratio

Figure 6 shows the average WeCE ratio of algorithms under different α.Before the UAV swarm enters into the saturation status(the saturation status refers to the moment when the task execution success ratio in most algorithms is less than 100%in Figure 5),we can see that the average WeCE ratio in DiMaToRe and MiWe-GRe is obviously lower than other algorithms,which is mainly because these two algorithms will try their best to request the most preferred SF for each task,and other algorithms have random properties when selecting the requested SFs for tasks.After the UAV swarm enters into the saturation status,as the number of tasks increases,the advantages of DiMaToRe and MiWeGRe fade away.This is mainly because the computation resources on UAVs are limited,it becomes very difficult for each task to get its most preferred SF,even a least preferred one,with the increase of the tasks.In addition,we can also see that the average WeCE ratio in DiMaToRe is smaller than that in MiWeGRe,which becomes more obvious as the number of tasks increases until the network is saturated.This is mainly because tasks with a larger average WeCE standard deviation are given priority to service in DiMaToRe algorithm.Furthermore,we calculate the average WeCE standard deviation of tasks under different α,which are 85.01,9.22 and 1.64 corresponding to α=1,α=0.1,α=0.001,respectively.We can find that the average WeCE standard deviation will decrease rapidly as α decreases.As shown in Figure 6,the advantages of DiMaToRe are also rapidly diminishing as α decreases.For example,when α is equal to 0.01,the average WeCE ratio in between DiMaToRe and MiWeGRe is approximate.Therefore,DiMaToRe proposed in this paper is very suitable for scenarios where the heterogeneity of computing resources is large.

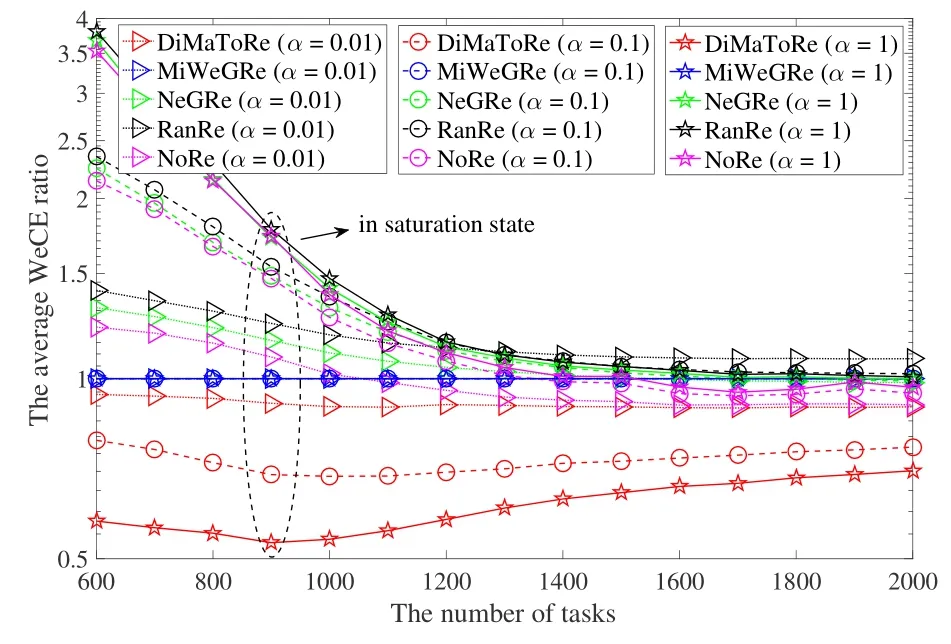
Figure 6. The average WeCE ratio under different α.

5.2.3 Analysis of the Average Satisfaction Degree Ratio

Figure 7 shows the average satisfaction degree ratio of algorithms under different α.The results show that the average satisfaction degree of tasks in DiMaToRe has been improved by 20%compared with MiWeGRe.This is mainly because DiMaToRe adopts a matching game framework and can achieve a stable matching,so that all tasks will simultaneously obtain best-possible SFs.We can see that the average satisfaction of tasks in NoRe,RanRe and NeGRe has always been lower than that in MiWeGRe.This is mainly because the SF requested by each task in these algorithms is not its most preferred SF.On the contrary,MiWeGRe tries its best to request the most preferred SF for each task.

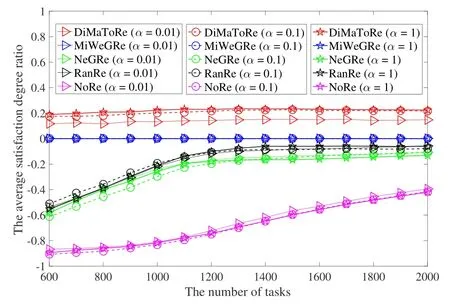
Figure 7. The average satisfaction ratio degree under different α.

5.2.4 Analysis of the Average Requesting Times

Figure 8 shows that the average requesting times of algorithms under different α.The results show that the average requesting times in DiMaToRe and Mi-WeGRe is more.This is because each task in Di-MaToRe and MiWeGRe firstly requests service from UAVs with high processing performance and low energy consumption,which will increase the probability of requesting failures and result in the increase of requesting times.Due to the limited computation resources of UAVs,as the number of tasks increases,the average requesting times also increase rapidly.In addition,we can see that the average requesting times in DiMaToRe is more than that in MiWeGRe.The reason mainly is: in MiWeGRe,the SF that has accepted a task’s request will reject the subsequent requests;on the contrary,in DiMaToRe,each SF only temporarily accepts a task,and reject it when receiveing a requesting of a more preferred task,so that the rejected task can only continue requesting the service from its next preferred SF.We can also see that the average requesting times in RanRe and NeGRe remains at a very low level before the UAV swarm overloads.This is mainly because the SF requested by each task in RanRe and NeGRe is randomly distributed on all UAVs,then the conflict probability of task requesting will be greatly reduced,so that the average requesting times of tasks is less.However,as the number of tasks increases,computation resources become insufficient,which increases the probability of requesting conflict,thereby resulting in a sharp increase of the average requesting times.

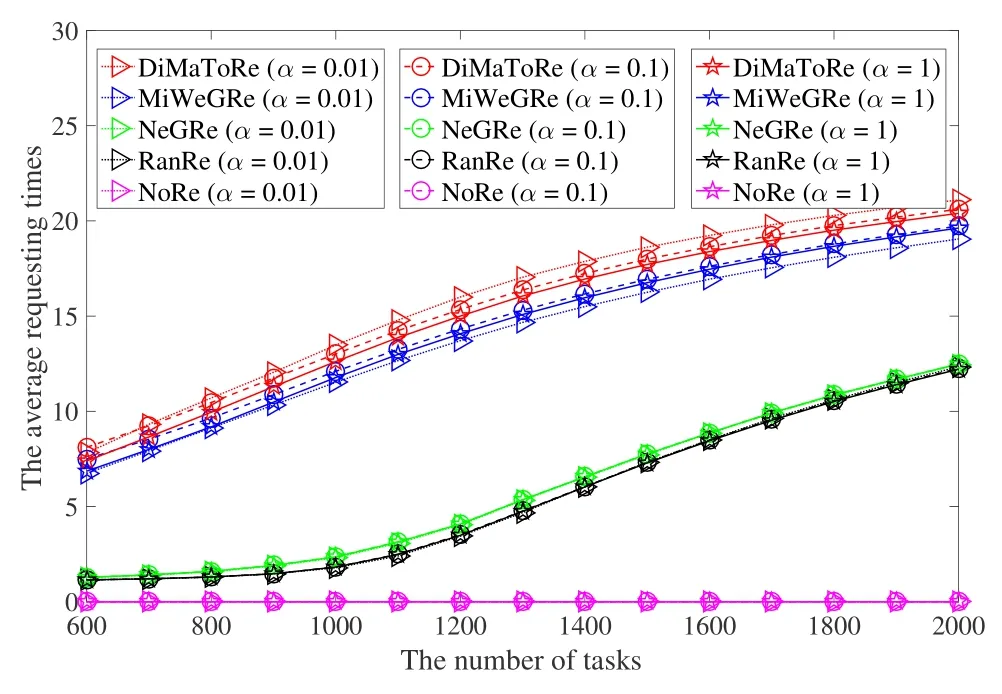
Figure 8. The average requesting times under different α.

5.2.5 Analysis of the Robustness

Different the general MEC,the instability of the wireless links between UAVs has to been considered since it challenges the robustness of our DiMaToRe.A link detection mechanism is designed to cope with it in DiMaToRe.Based on this mechanism,a few more simulations are conducted to evaluate the robustness of DiMaToRe with different aerial link failure ratios(i.e.,5%,10%,and 20%)with different UAV densities.Here,UAV density is measured by the Average Number of the Neighbors of a UAV (ANN),and the Link Failure Ratio (LFR) refers to the ratio of the number of failed aerial links to the total number of aerial links of a UAV.

Figure 9 illustrates the evaluation results.The results show that even if the link failure between UAVs reduces the average execution success ratio of tasks,DiMaToRe can still work stably,showing good robustness.The reasons are mainly twofold: first,the UAVs in DiMaToRe only shares resources with its one-top neighbors,which greatly reduces the impact range of a failed link;second,a link detection mechanism in DiMaToRe enables UAVs to share resources only with neighbors with stable links.In addition,one can see that in a densely deployed UAV swarm,little impact can be observed when the link failure ratio is lower than 10%.For instance,when ANN=30 and LFR=5%,its impact is negligible.This is also reasonable since each UAV has a large number of candidate neighbors and sufficient computing resources are available.When LFR is as large as 20%,it can decrease the average execution success ratio of tasks by about 10% under different parameter settings,and its impact is independent of the density of the UAVs.For example,when ANN=10,even if the value of LFR is equal to 0 and task load is light,the average task execution success ratio is still very low.To sum up,the essence that can affect the average task execution success ratio is the number of candidates neighbors(i.e.,the capacity of available computation resources),rather than the value of a single ANN or LRF.

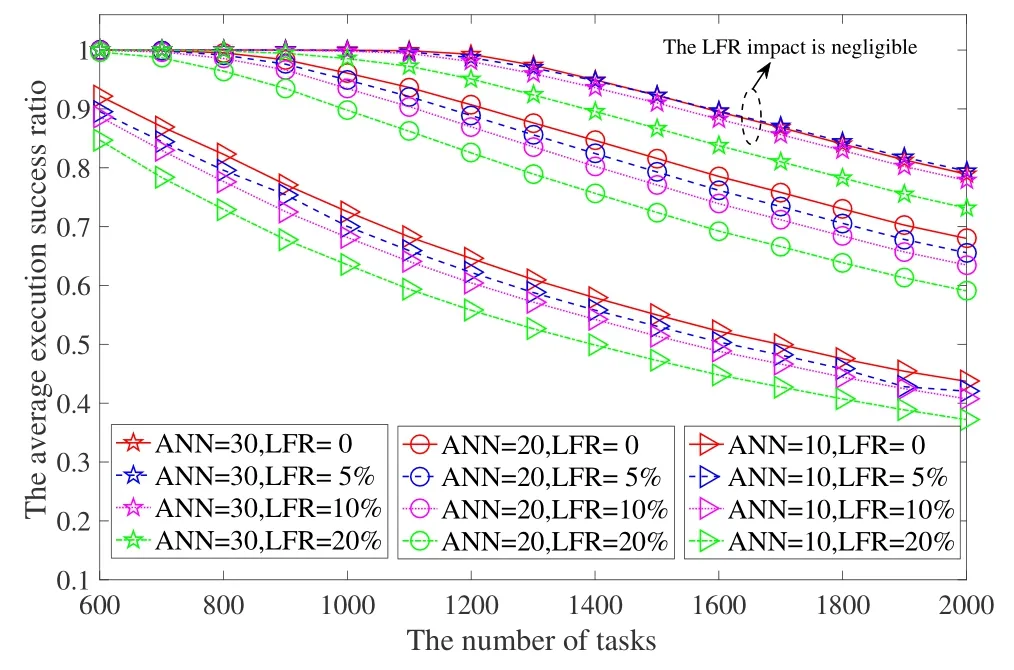
Figure 9. The average task execution success ratio of Di-MaToRe under the different ANNs and ALFRs.

VI.CONCLUSION

In this paper,we study a task scheduling problem based on the distributed,heterogeneous and multi-UAV edge computing for maximizing the task execution success ratio and minimizing the average WeCE per bit task.We design a time slot partitioning protocol,and propose a Distributed Matching Theorybased Re-allocating algorithm running on this protocol,which can obtain a stable matching between tasks,SFs and UAVs within each time slot.To cope with the instability of the wireless link between UAVs,a link detection mechanism is designed to ensure the robustness of our proposed algorithm.Experimental results show that DiMaToRe can effectively improve the task average execution success ratio and the average task satisfaction degree,reduce the average WeCE per task bit compared with the benchmarks,and has good robustness.In the future work,we intend to take the deployment of UAV hover positions into account,further improve the computing service efficiency of multi-UAV edge computing system.

ACKNOWLEDGEMENT

This work was supported by the National Natural Science Foundation of China under Grant 62171465.

APPENDIX

A Validation of the UAV Preference

Here is a proof that the UAV preference designed in this paper can reduce the total sum of all tasks’WeCE.

Eq.(A.4)is subtracted from Eq.(A.3)to obtain the following:

According to the above assumption condition,we can infer that △＜0 holds,which shows that our proposed preference principle can reduce the total sum of all tasks’WeCE.Especially when the WeCE value of tasks executed on different SFs fluctuates more,that is,the greater the SFs heterogeneity,the bigger the value of|△|.