Adaptive Bistable Stochastic Resonance Based Weak Signal Reception in Additive Laplacian Noise

Jin Liu ,Zan Li ,Qiguang Miao ,Li Yang

1 School of Computer Science and Technology,Xidian University,Xi’an 710071,China

2 State Key Laboratory of Integrated Services Networks,Xidian University,Xi’an 710071,China

Abstract: Weak signal reception is a very important and challenging problem for communication systems especially in the presence of non-Gaussian noise,and in which case the performance of optimal linear correlated receiver degrades dramatically.Aiming at this,a novel uncorrelated reception scheme based on adaptive bistable stochastic resonance(ABSR)for a weak signal in additive Laplacian noise is investigated.By analyzing the key issue that the quantitative cooperative resonance matching relationship between the characteristics of the noisy signal and the nonlinear bistable system,an analytical expression of the bistable system parameters is derived.On this basis,by means of bistable system parameters self-adaptive adjustment,the counterintuitive stochastic resonance(SR)phenomenon can be easily generated at which the random noise is changed into a benefit to assist signal transmission.Finally,it is demonstrated that approximately 8dB bit error ratio (BER) performance improvement for the ABSR-based uncorrelated receiver when compared with the traditional uncorrelated receiver at low signal to noise ratio (SNR) conditions varying from-30dB to-5dB.

Keywords: adaptive bistable stochastic resonance;additive Laplacian noise;low signal to noise ratio;uncorrelated reception scheme;weak signal reception

I.INTRODUCTION

This paper is concerned with the reception performance of the weak signal in additive non-Gaussian noise.The so-called“weak signal”means that the signal is small when compared with the additive background noise.The weak signal reception has got a great deal of attention for the low intercept probability and high anti-jamming capability demands of modern communication systems[1–4].Although a Gaussian noise assumption to be usually justified,there are many practical application scenarios in which the background noise is not Gaussian,such as signal processing systems[5–7],cognitive radio systems[8,9],internet of things[10,11],power systems[12]and so on.As is known to all,on one hand,according to the statistical signal processing theory,the reception performance of the linear correlated receiver is optimal under Gaussian white noise and degrades dramatically if the background noise is non-Gaussian.On the other hand,uncorrelated receiver has relatively lower computation complexity when compared with the correlated receiver,which can be considered to apply to signal reception in non-gaussian noise conditions.However,the reception performance of uncorrelated receiver is far from satisfactory in strong non-Gaussian background noise environment as well,as shown in Figure 1[13].

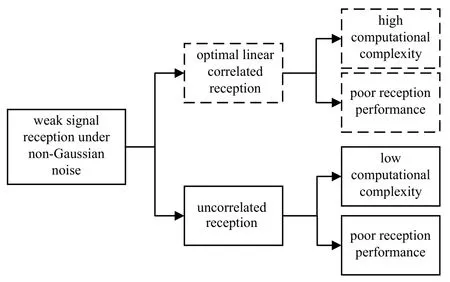
Figure 1.Weak signal reception under non-Gaussian noise.

For noise is commonly perceived as one of the main reasons for reception performance deterioration,and traditional linear signal processing methods are generally implemented by means of noise suppression,whose signal processing performance turned out to be unsatisfactory at low signal-to-noise ratio(SNR)situations [14–16].Aiming at this issue,a novel signal processing method using stochastic resonance (SR)has been proposed.Traditional stochastic resonance(TSR) is given to a phenomenon of noise-assisted weak periodic signal transmission taking place in a nonlinear bistable system,revealing a role change of the noise from a nuisance into a favorable factor[17–22].In view of this,the counterintuitive SR phenomenon attracts considerable attention in different application areas such as biological systems [23–25],optical systems [26,27],quantum physics [28,29],fault diagnosis[30–32],communication systems[33–35]and so on.

With the deepening of research on SR,more attention has been focused on the information-carrying aperiodic signal processing via SR technique,i.e.,aperiodic stochastic resonance (ASR),which is of more practical application value in wireless communications [36–38].ASR system can be carried out by means of adding noise or tuning system parameters.In contrast,system parameter tuned method is more feasible and flexible especially when the background noise is strong enough to exceed the demanded level for the ASR effect [39–42].Even so,the existing researches on parameter tuned ASR method are still mainly confined to additive Gaussian white noise assumption [40–45].Aiming at the application requirements for weak signal reception performance improvement under non-Gaussian noise,it is of great significance to carry out research on ASR mechanism in non-Gaussian noise conditions.In the article,Laplacian noise is selected to model non-Gaussian noise mainly for two reasons.On one hand,both the Laplacian noise and Gaussian white noise can be seen as a special case of Generalized Gaussian noise,and the quantitative research on ASR can be greatly simplified when Laplacian noise is used to model non-Gaussian noise.On the other hand,Laplacian noise itself exists in a wide range of applications such as wireless communication systems[46,47],cognitive radio systems[48],electrode location of the electrocardiogram(ECG) signal processing [49],watermark extraction in discrete cosine transform (DCT) domain [50] and so on,and the research results of this paper can be applied to related fields under Laplacian noise environment.The main contribution and novelty of the paper is to study the quantitative resonance mechanism of ASR system and extend the ASR technique to the application of weak signal reception under Laplacian noise.By drawing on the core idea of transfer learning,the equivalent cooperative resonance effect is analyzed in detail under Gaussian white noise and Laplacian noise.On this basis,the quantitative cooperative resonance matching relationship under Laplacian background noise is induced,then the adaptive bistable stochastic resonance (ABSR) system can be realized by bistable system parameters self-adaptive adjustment,which assure the output signal of ABSR system to be in the resonant state.Further,by introducing the ABSR system as the pre-enhancement processing unit for traditional uncorrelated receiver,a novel uncorrelated reception scheme based on ABSR system is proposed,and the corresponding reception performance is studied through theoretical analysis and numeric simulation,as shown in Figure 2.

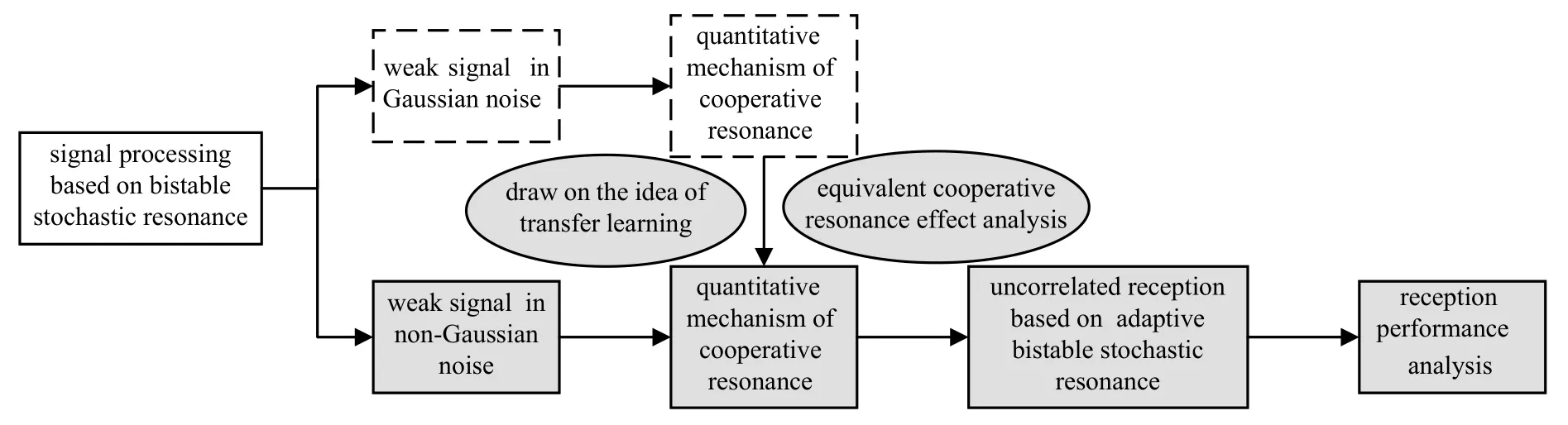
Figure 2. Research ideas and structure of this paper.

The structure of this article is formed as follows.Quantitative cooperative resonance matching relationship under Laplacian background noise is discussed in Section II.Design and performance analysis of the ABSR-based uncorrelated receiver is given in Section III.In Section IV,simulation results are provided,and finally conclusions are made in Section V.

II.QUANTITATIVE COOPERATIVE RESONANCE MATCHING RELATIONSHIP

In this paper,the bistable system with the most obvious nonlinear characteristics is chosen as the SR system,and the classical bistable stochastic resonance(BSR)theoretical research is usually based on additive Gaussian white noise assumption.Therefore,BSR system response to aperiodic binary pulse amplitude modulated(BPAM)signal under a certain level of additive Gaussian white noise is first analyzed in this section.On this basis,by analyzing the equivalent cooperative resonance effect under Gaussian white noise and Laplacian noise,the quantitative cooperative resonance matching relationship under Laplacian background noise is researched thoroughly.

2.1 In-Depth Analysis of Aperiodic Stochastic Resonance(ASR)Principle

To simplify the theoretical analysis of the ASR principle,the input signal of the BSR system is assumed to be aperiodic bipolar BPAM signals s(t) with the following expression.

Here,A is the signal amplitude,and G(t) is a unit gate function of duration T,i.e.,G(t)=1 for t ∈(0,T) and G(t)=0 otherwise.The BPAM symbols Si,i integer,are variables of independent identically distribution,i.e.,P(Si=1)=P(Si=−1)=.

Assume the background noise ξ(t) obeying zero mean σ2=2D variance additive Gaussian white noise distribution,noise intensity D,i.e.,〈ξ(t)ξ(t+τ)〉=σ2δ(τ)=2Dδ(τ),where 〈·〉 and δ(·) separately are the autocorrelation function and dirac function.

The BSR system output signal x(t)obeys Langevin equation with the action of the input BPAM signal s(t)and additive Gaussian white noise ξ(t)[43,44].

The free relaxation of the BSR system,denoted as dx/dt=−dU/dx,depends on the quartic potential U(x)=−ax2/2+bx4/4 −x(s(t)+ξ(t)).Here,a and b are the parameters of the BSR system with positive value(a ＞0,b ＞0).

Langevin equation describes the macroscopic manifestation of brownian motion,in which the bistable system with the quartic potential U(x)can be seen as the motion trail of the brownian particle.By analogy analysis with the principle of the brownian motion,a brief principle of the ASR system can be stated as follows.

(1)Without regard to the interaction of the ordered force s(t)and the stochastic force ξ(t),the stable equilibrium states of the bistable system are separately located at the two minima of the BSR system quartic potential x=,and the height of quartic potential is ΔU=a2/4b,as shown in Figure 3(a).

Figure 3. Quartic potential,a=1,b=1,ξ(t)=0.

(2) With regard to the interaction of the ordered force s(t),an ordered tilt is taken place in the quartic potential of the bistable system U(x).The threshold of the BSR system is ThBSR=,as shown in Figure 3(c),by which the input signals are divided into subthreshold signals when the BPAM amplitude A ＜ThBSRand superthreshold signals otherwise,as shown in Figure 3(b)and Figure 3(d).

1) With superthreshold signals input force (A ＞ThBSR),the energy of the brownian particle(bistable system output signal x(t))can overcome the obstacle of the height of quartic potential ΔU=a2/4b even without the aid of the stochastic force ξ(t),at which the favorable effect of the stochastic force ξ(t)has not embodiment obviously,as shown in Figure 3(d).

2) By contrast,bistable system with subthreshold weak signals input force(A ＜ThBSR)should be paid more attention.In this situation,only if with the aid of the energy of the stochastic force ξ(t),the energy of the brownian particle x(t) can overcome the obstacle of the height of quartic potential ΔU=a2/4b,then the brownian particle x(t) can hop from one potential to the other of the bistable system by the cooperative effect of the ordered force s(t)and the stochastic force ξ(t),at which the favorable effect of the stochastic force ξ(t) has embodiment obviously.Besides,the output signal of the bistable system x(t) is enhanced apparently when compared with the input ordered force s(t),i.e.,noise assist signal transmission,as shown in Figure 3(b).Meanwhile,considering the characteristics of the weak signal itself,BSR system with subthreshold weak signals input is mainly discussed in the article.

(3) Further,with regard to the interaction of both the subthreshold ordered force s(t) and the stochastic force ξ(t),the principle of the ASR system should be made clearer and more detailed in light of the goal of the application domain.Import of the ASR theory in the field of weak signal reception,showing the advantage of using noise to enhance the weak signal,and improving the weak signal reception performance are important tasks.In other words,the higher reception accuracy should be generated by processing the BSR system output signal x(t) when compared with directly processing the received signal r(t)=s(t)+ξ(t).

For the Gaussian white noise processed by BSR system is no longer obeying Gaussian distribution,but obeys Lorentz distribution.Therefore,uncorrelated reception is commonly used to deal with the bistable system output signal x(t)as follows.

where the symbol interval parameter T is often assumed to be known in signal reception.The present transmitted symbols Si=+1 (or Si=−1) can be correctly recovered at the decision time t=ti+T when the BSR system output signal x(t)has been right in the neighborhood of the stable state x=(or x=),i.e.,the present decision result Xito be Xi=+1 (or Xi=−1),with the signal amplitude switching from −A to+A(or+A to −A).It requires that the BSR system response time Tr(time t0to t2),denoting the time taken by the BSR system output signal x(t)to switch from one potential well to the other motivated by r(t)=s(t)+ξ(t),to be shorter than the symbol interval T,i.e.,Tr＜T,as shown in Figure 4(b).

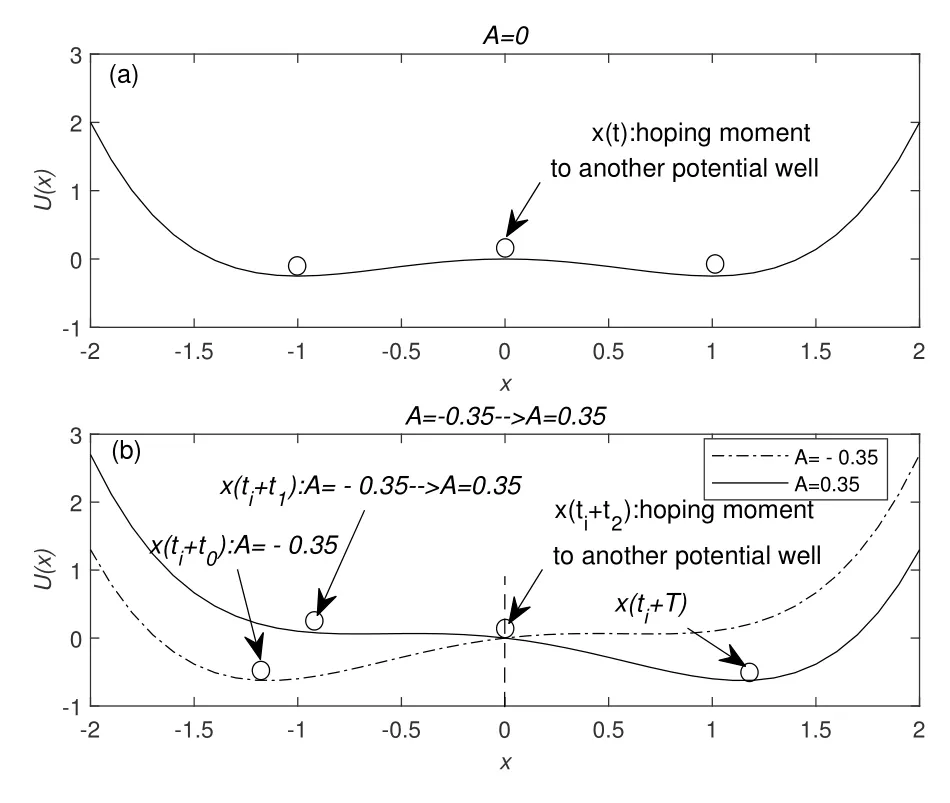
Figure 4. BSR system output state in quartic potential,a=1,b=1.

In classical adiabatic approximation theory (A ≪1,T ≫1,D ≪1),the mean first-passage time Tkis defined as the mean transition time of the output signal x(t) transferring between the BSR system potential wells,which is motivated only by the random noise(A=0),referring to Figure 4(a)[19].

From a comparison of physics significance,the mean first-passage time Tkmotivated by the noise only is obviously longer than the BSR system response time Trwhich is motivated by both the signal and the noise,i.e.,Tk＞Tr.Therefore,the condition for correctly recovering the transmitted symbols can be further expressed as Tk＜T.In a certain level of background noise intensity D,the parameter Tkcan be realized through BSR system parameters a and b adjustment as shown in Eq.(4).The relationship Tk＜T can be seen as the time matching characteristics of the BSR system.

Moreover,it has been testified that the output of BSR system is in the optimal state when the noise intensity D is equivalent to the BSR system potential height ΔU [44].With too small noise,the contribution of noise energy cannot lead to the BSR system output hopping between the two stable equilibrium states of the BSR system.With too much noise,the cooperative resonance effect subsides for part of the noise infeed the noise out.Therefore,the relationship D=ΔU can be seen as the amplitude matching characteristics of the BSR system.

Under adiabatic approximation premise,the ASR phenomenon is assured to occur when the time matching characteristics and amplitude matching characteristics of the BSR system are fulfilled simultaneously.Therefore,the BSR system with parameters a=1,b=1 and input noisy BPAM signal of value T0=100s ＞Tk=12.07s ＞Tr,D0==ΔU=a2/4b=0.25,A0＜ThBSR≈0.38 is called a normalized aperiodic stochastic resonator (NASR)[44].

Here,n(t) is a zero-mean and unit variance Gaussian white noise.

In practical wireless communication systems,the characteristics of the signal and background noise usually not satisfies the adiabatic approximation premise,i.e.,(T ≪1,D ≫1).Therefore,by linear transformation of Eq.(2)with the form τ=at,y=,it is not difficult to get

By means of BSR system parameter self-adaptive adjustment according to the characteristics of the signal and noise as shown in Eq.(7),the ASR phenomenon is ensure to occur in practical wireless communication application scenario.Even so,it is regret to find that the above conclusion to be only applicable in Gaussian white noise assumption.Aiming at this,this paper further extends the ASR theory to the application scenario of weak signal reception under a typical non-Gaussian background noise,namely Laplacian noise.

2.2 Quantitative Cooperative Resonance Matching Relationship Under Laplacian Noise

It is hard to get an analytical solution for Langevin equation which is a nonlinear stochastic differential equation,as shown in Eq.(2).Therefore,four-stage Runge-Kutta iterative method is commonly used for numerical solution of Langevin equation,considering the interpolation of the input noisy signal during the slope calculation.

where sn,ξn,rn,xnseparately are the nth sample value of the input BPAM signal s(t),background noise ξ(t),noisy signal r(t)=s(t)+ξ(t)and BSR system output signal x(t),and h is the numeric calculation step size.Here,k1,k2,k3and k4are four slopes of the single-step iterative calculation.

Considering the situations that the background noise ξ(t) to be Gaussian white noise and Laplacian noise respectively,parameters hGand hLare defined as the numeric calculation step size under Gaussian white noise and Laplacian noise separately.In the background of Gaussian white noise,theoretical derivation and numerical simulation experiment has been demonstrated that the relationship ahG＜0.5 to be the stability condition of the four-stage Runge-Kutta numerical simulation [51].Without loss of generality,the value of numeric calculation step size hGis usually selected to be ahG=0.45,i.e.,hG0=0.45/a0,a0=1 for the NASR model as shown in Eq.(5) and hG=0.45/a for practical wireless communication signal processing with the parameter a to be set as in Eq.(7).

By drawing on the core idea of transfer learning,the equivalent cooperative resonance effect is analyzed under Gaussian white noise and Laplacian noise.

First,assume the background noise ξ(t) obeying Gaussian white noise distribution,whose probability density function(PDF)is denoted as G(x).

where parameters µ and σ separately are the mean value and the standard deviation of the Gaussian white noise.Parameterµalso is the positional parameter of the PDF curve G(x),that is to say,G(x) obeying a normal distribution centered on x=µ.Parameter σ is the scale parameter of the PDF curve G(x),which describes the dispersion of data distribution.The greater the σ,the more dispersed the data distribution,and the smaller the σ,the more concentrated the data distribution.

Similarly,assume the background noise ξ(t)obeying Laplacian noise distribution,whose PDF is denoted as L(x).

where parametersµand λ separately are the positional parameter and scale parameter of the Laplacian distribution PDF curve L(x).

The positional parameter of the G(x)and L(x)are assumed to be µ=0.Based on statistical theory,it is easy to get that the average power of the Gaussian white noise and Laplacian noise are separately to be σ2and 2λ2.The PDF curves of Gaussian white noise and Laplacian noise with the same average power σ2=2λ2=1 are shown in Figure 5.

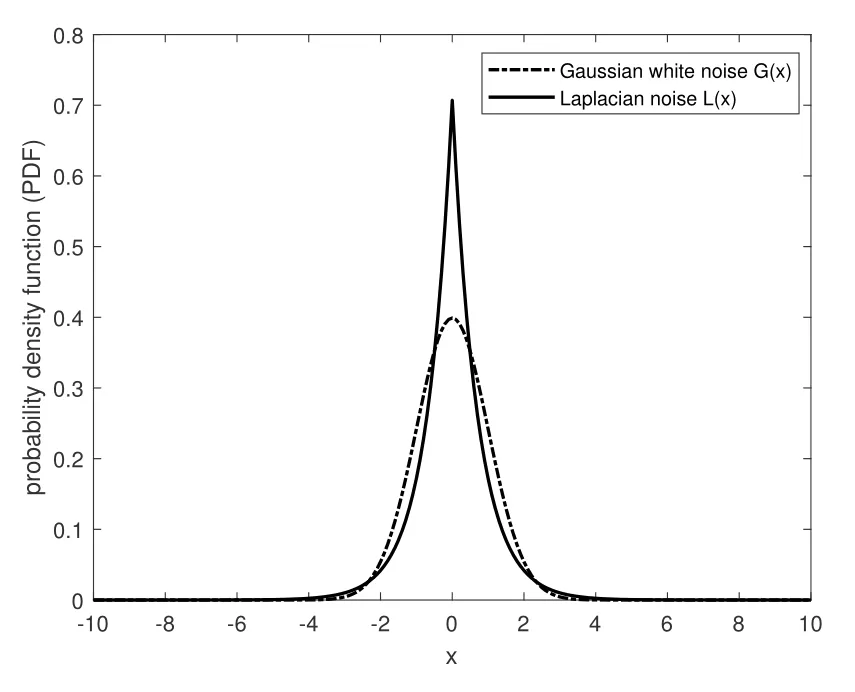
Figure 5. The PDF curves of Gaussian white noise and Laplacian noise.

In the condition that the Gaussian white noise and Laplacian noise with the same average power,i.e.,σ2=2λ2,it can be easily induced that the scale parameter of Gaussian white noise and Laplacian noise satisfying λ=.As the scale parameter describing the dispersion of data distribution,the smaller value of λ means that the more concentrated data distribution of Laplacian noise compared with that of the Gaussian white noise,and the smaller numeric calculation step size should be required for the stability conditions of the four-stage Runge-Kutta numerical simulation method accordingly in Laplacian noise.Therefore,it comes to a conclusion that the numeric calculation step size should satisfying the following relationship to assure the equivalent cooperative resonance effect under Gaussian white noise and Laplacian noise with the same average power.

On this basis,the quantitative cooperative resonance matching relationship under Laplacian background noise is induced,and the NASR model under Laplacian noise is established.

Further,through similarly linear transformation as in Gaussian white noise condition,quantitative cooperative resonance matching relationship under Laplacian background noise is proposed.

In practical wireless communication systems under Laplacian noise,the ASR phenomenon can be ensured to occur through bistable system parameters a and b self-adaptive adjustment according to Eq.(13).

III.IMPLEMENTATION AND PERFORMANCE ANALYSIS OF ADAPTIVE BISTABLE STOCHASTIC RESONANCE (ABSR) BASED UNCORRELATED RECEIVER

Based on analyses of the quantitative cooperative resonance relationship above,the definition of adaptive bistable stochastic resonance(ABSR)is given as: according to the characteristics of signal and noise,the parameters of the bistable system are adjusted adaptively so that the output signal of the bistable system is in the resonance state.More precisely,combined with the main purpose of using the ABSR technique to improve the uncorrelated reception performance of the weak BPAM signal under Laplacian noise in this article,the definition of ABSR can further be given as: according to the characteristics of the BPAM signal(symbol interval T which is assumed to be known at the uncorrelated receiver)and Laplacian noise(average power 2λ2which is estimated by second order fourth moments (M2M4) estimation method given in the following part),the ABSR system can easily be implemented by bistable system parameters a and b self-adaptive adjustment,as shown in Eq.(13),and the realization of the ABSR system assures that the output signal of the ABSR system is in the resonance state at the decision time of the uncorrelated receiver.Further,the framework of ABSR-based uncorrelated receiver is established by introducing the ABSR system as the pre-enhancement signal processing unit for traditional uncorrelated receiver,as shown in Figure 6,which has advantage of improving the BER performance of the traditional uncorrelated receiver at low SNR conditions.

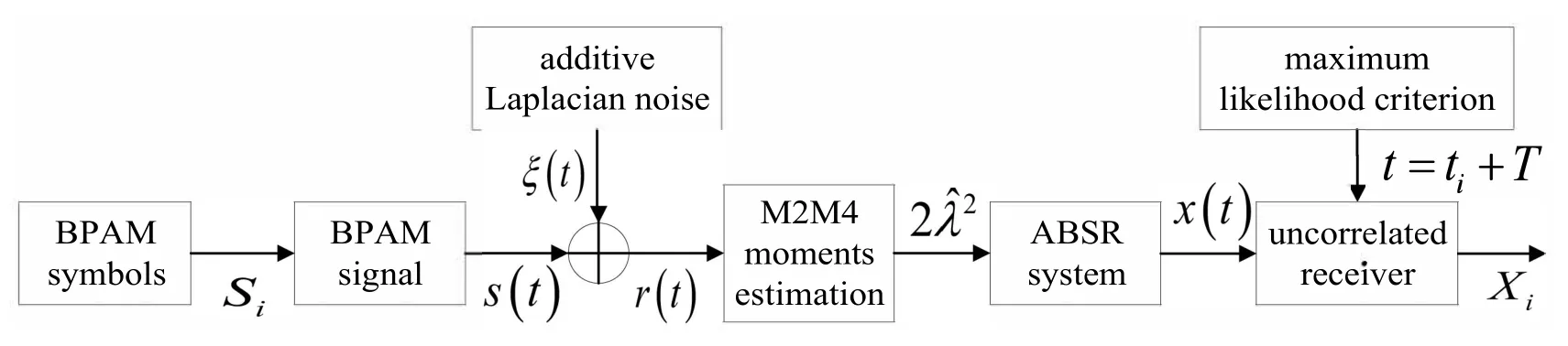
Figure 6. Framework of ABSR-based uncorrelated receiver.

3.1 Implementation of the ABSR-Based Uncorrelated Receiver

Frist,second order fourth moments estimation(M2M4)method is used to blind estimate the average power of Laplacian noise.

where parameters S and N separately are the average power of the BPAM signal and Laplacian noise,and parameters ks=and kξ=separately are the kurtosis coefficient of the sinal and noise,in which snand ξnare the nth sample value of the input BPAM signal s(t) and background noise ξ(t).For BPAM signal and real Laplacian noise,the value of kurtosis coefficients are ks=1 and kξ=6 respectively.

Then from the relationship shown in Eq.(14),the estimated value of the average power of Laplacian noisecan be calculated as follows.

In practice,second order quantities M2and fourth order quantities M4are derived from the time average of the receiving sequences,i.e.,M2≈and M4≈,where r(n) and L are the nth sample value and sampling length of the received noisy signal r(t)=s(t)+ξ(t).

Next,by BSR system parameters a and b selfadaptive adjustment according to Eq.(13),the realization of the adaptive bistable stochastic resonance(ABSR) system is accomplished,which ensures the ASR phenomenon generation at the decision time of the uncorrelated receiver.

Further,the uncorrelated receiver is used to process the ABSR system output x(t) as shown in Eq.(3),at which ABSR system output x(t) is right in the neighborhood of the stable state x=(or x=).It means that the present transmitted BPAM symbols Si=+1 (or Si=−1) can be correctly recovered by the corresponding decision results Xi=+1(or Xi=−1).

3.2 Performance Analysis of the ABSR-Based Uncorrelated Receiver

For the background noise ξ(t) obeying a zero-mean and average power 2λ2Laplacian distribution,then the probability density function(PDF)of the received signal r(t)=s(t)+ξ(t)can be expressed as follows.

The optimal decision threshold of the traditional uncorrelated receiver r0=0 can be easily derived based on maximum-likelihood (ML) criterion,i.e.,p(r0|s(t)=+A)=p(r0|s(t)=−A).Based on the apriori knowledge that BPAM signal obeying identically probability distribution,i.e.,p(s(t)=+A)=p(s(t)=−A)=1/2,the bit error ratio (BER) expression of the traditional uncorrelated receiver,denoted as Pe,can be derived.

The Fokker-Planck(FP)equation for the probability density of the ABSR system output signal p(x,t) is given as follows[41,52].

where Diffcoe−Lis defined as the equivalent diffusion coefficient for Laplacian noise which is similar to the diffusion coefficient D in Gaussian white noise conditions.The mechanism of the ABSR system shown in Eq.(13)assures that the output signal x(t)to be right in the neighborhood of the stable state x(t)=at the decision time t=ti+T.Then the asymptotic steady-state solution of the FP equation is deduced as follows.

where parameters C1and C2are constants determined by the normalization of the probability density=1 and=1 respectively.The quartic potential of ABSR system can be expressed as U1(x)=−ax2/2+bx4/4 −Ax (or U2(x)=−ax2/2+bx4/4+Ax)when the bipolar BPAM signal amplitude to be s(t)=+A(or s(t)=−A).

Similarly,for the symmetry property of the ABSR system quartic potentials U1(x) and U2(x),the optimal decision threshold of the ABSR-based uncorrelated receiver x0=0 can also be derived based on ML criterion i.e.,p(x0|s(t)=+A)=p(x0|s(t)=−A).Then the BER expression of the ABSR-based uncorrelated receiver,denoted as P′e,can be derived as follows.

Here,the value of the ABSR system parameters a and b are configurated according to Eq.(13).For Eq.(20) containing non-integrable terms such as∫exp（x2）dx and∫exp（x4）dx,therefore,it is the simplest form of the BER expression for ABSR-based uncorrelated receiver.

IV.SIMULATION RESULTS

4.1 NASR Model Under Gaussian White Noise

Considering the situation that the subthreshold BPAM signal amplitude to be A0=0.35 ＜ThBSR≈0.38,the symbol interval T0and the Gaussian white noise varianceare set with the value T0=100s,=0.5.For NASR model,bistable system parameters are set with the unit value,i.e.,a0=1,b0=1.The value of numeric calculation step size hG0is selected to be hG0=0.45/a0=0.45,and the number of BPAM symbols is chosen as N=30.

Figure 7 shows the BSR system responding to the BPAM signal in Gaussian white noise under adiabatic approximation premise,in which both the time matching characteristic(Tr＜Tk=12.07s ＜T0=100s)and the amplitude matching characteristic (D0==0.25) that required for cooperative resonance mechanism of the BSR system are satisfied simultaneously,ensuring the ASR phenomenon generation in Figure 7.Figure 7(a)shows the transmitted BPAM signal s(t).Figure 7(b)shows the Gaussian white noise ξ(t).Figure 7(c)shows the received noisy signal r(t)=s(t)+ξ(t).Figure 7(d)shows the output signal x(t) of the NASR model.The simulation result in Figure 7 verifies the correctness of the theoretical analysis of the NASR model (in adiabatic approximation premise) under Gaussian white noise,as shown in Eq.(5).

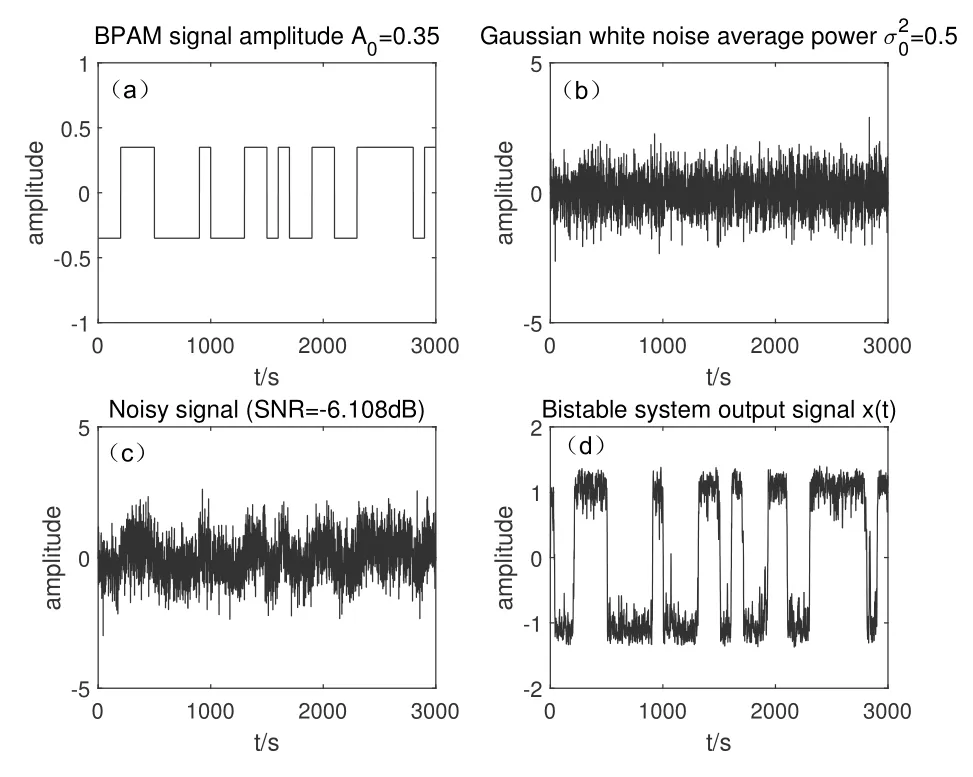
Figure 7. NASR model simulation in Gaussian white noise.

4.2 NASR Model Under Laplacian Noise

Considering the situation that the BPAM signal amplitude to be A0=0.35,the symbol interval T0and the average power of Laplacian noiseare set with the value T0=100s,=0.5.For NASR model,the bistable system parameters are set with the unit value,i.e.,a0=1,b0=1.The value of numeric calculation step size hL0is selected to be hL0=,and the number of BPAM symbols is chosen as N=30.

Figure 8 shows BSR system responding to the BPAM signal in Laplacian noise under adiabatic approximation premise,and the ASR phenomenon can be clearly seen in Figure 8 as well.Figure 8(a)shows the transmitted BPAM signal s(t).Figure 8(b)shows the Laplacian noise ξ(t).Figure 8(c) shows the received noisy signal r(t)=s(t)+ξ(t).Figure 8(d)shows the output signal x(t)of the NASR model.The simulation result in Figure 8 verifies the correctness of the theoretical analysis of the NASR model (in adiabatic approximation premise) under Laplacian noise,as shown in Eq.(12).

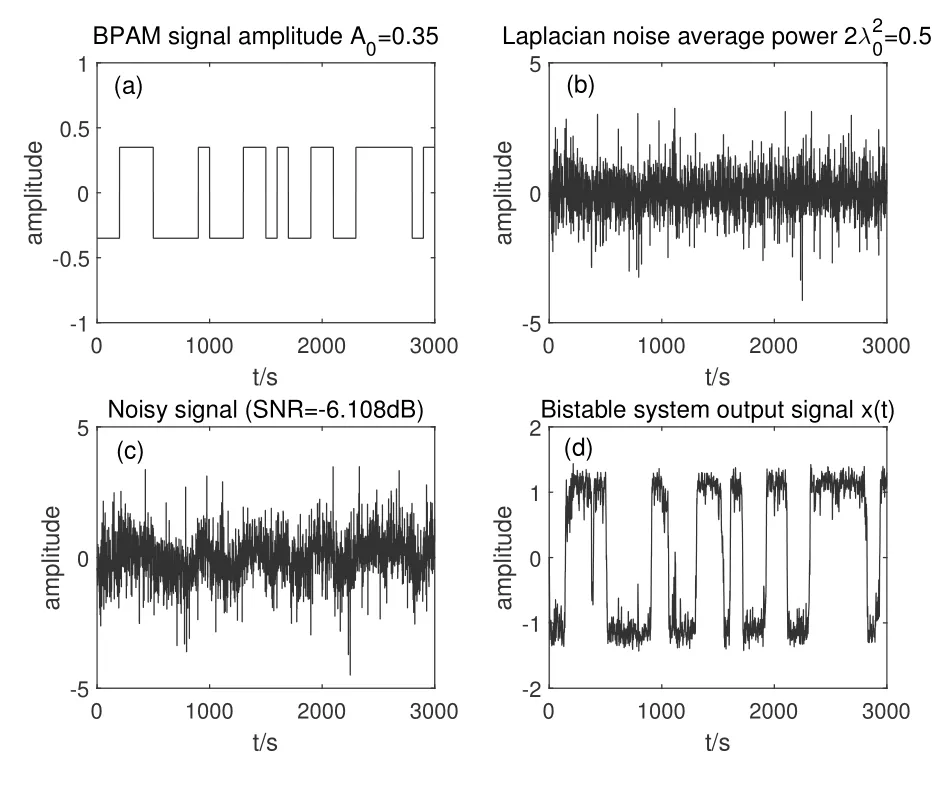
Figure 8. NASR model simulation in Laplacian noise.

By comparing simulation results of Figure 7 and Figure 8,it proves the validity of the quantitative cooperative resonance matching relationship for the NASR model under Laplacian background noise as shown in Eq.(12).

4.3 ABSR-Based Signal Processing Under Gaussian White Noise

Without the limitation of adiabatic approximation condition,it seems reasonable to suppose that the BPAM signal amplitude A,the symbol interval T and the Gaussian white noise variance σ2to be set with the value A=1,T=0.01s,σ2=5,in practical wireless communication situations.For ABSR-based signal processing model,the parameters of the bistable system are set according to Eq.(7),a=10000,b=1011.The value of numeric calculation step size hGis selected to be hG=0.45/a,and the number of BPAM symbols is chosen as N=30.

Figure 9 shows ABSR system responding to the BPAM signal under Gaussian white noise in practical wireless communication scenarios,in which case the characteristics of the BPAM signal and Gaussian white noise are not limited to adiabatic approximation premise.At this point,the ASR phenomenon can be clearly seen in Figure 9.Figure 9(a)shows the transmitted BPAM signal s(t).Figure 9(b)shows the Gaussian white noise ξ(t).Figure 9(c)shows the received noisy signal r(t)=s(t)+ξ(t).Figure 9(d) shows the output signal x(t)of the ABSR system.The simulation result in Figure 9 verifies the correctness of the theoretical analysis of the ABSR-based signal processing(without the limitation of adiabatic approximation condition) under Gaussian white noise,as shown in Eq.(7).

4.4 ABSR-Based Signal Processing Under Laplacian Noise

Considering the practical wireless communication situations that the BPAM signal amplitude to be A=1,the symbol interval T and average power of Laplacian noise 2λ2are set with the value T=0.01s,2λ2=5.For ABSR-based signal processing model,the parameters of the bistable system are set according to Eq.(13),a=10000,b=1011.The value of numeric calculation step size hLis selected to be hL=,and the number of BPAM symbols is chosen as N=30.

Figure 10 shows ABSR system responding to the BPAM signals under Laplacian noise in practical wireless communication scenarios.Figure 10(a)shows the transmitted BPAM signal s(t).Figure 10(b) shows the Laplacian noise ξ(t).Figure 10(c) shows the received noisy signal r(t)=s(t)+ξ(t).Figure 10(d) shows the output signal x(t) of the ABSR system.It is obviously that the ASR phenomenon to be clearly seen in Figure 10,which makes the ABSR-based uncorrelated receiver easier to make the right decision by comparing decision results Xi=sign(x(ti+T))with transmitted BPAM symbols Si,when compared with the traditional uncorrelated receiver to make the decision by comparing decision results Ri=sign(r(ti+T)) with transmitted BPAM symbols Si.The simulation result in Figure 10 verifies the correctness of the theoretical analysis of the ABSR-based signal processing(without the limitation of adiabatic approximation condition)under Laplacian noise,as shown in Eq.(13).

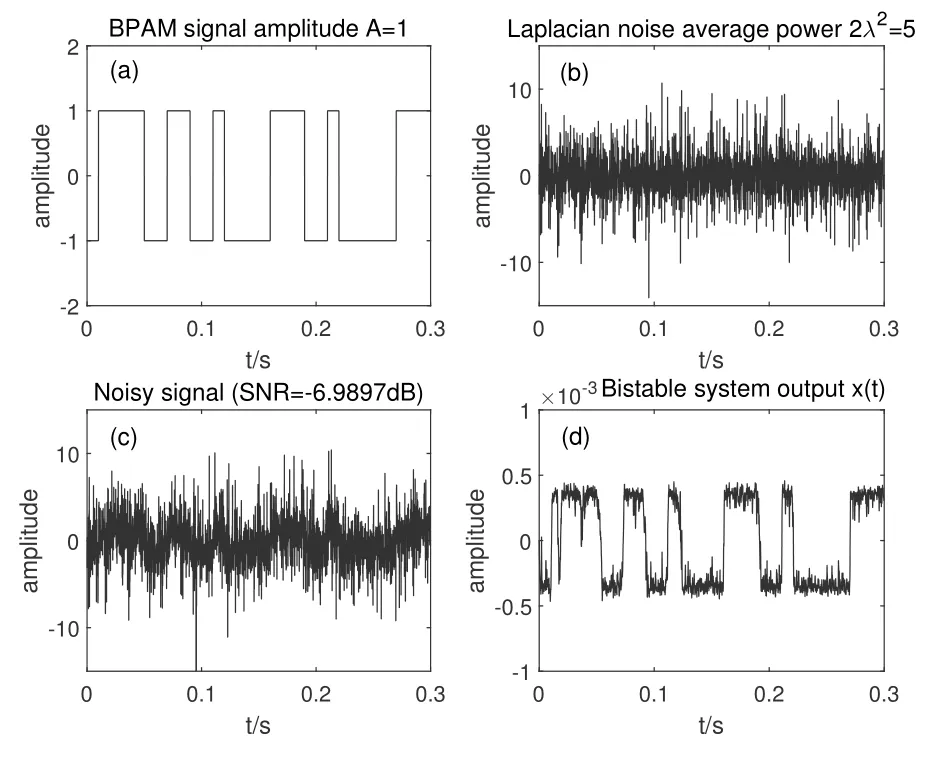
Figure 10. ABSR-based signal processing under Laplacian noise.

From a comparison of the ABSR-based practical wireless communication signal processing simulation results of Figure 9 and Figure 10,it proves the validity of the quantitative cooperative resonance matching relationship under Laplacian background noise as shown in Eq.(13).

4.5 Bit Error Ratio(BER)Performance of the ABSR-Based Uncorrelated Receiver

In this section,the BER performance simulation result is provided averaged over 105sampling points Monte Carlo method to evaluate the reception performance of the ABSR-based uncorrelated receiver.

Figure 11 reveals the low SNR conditions varying from -30dB to -5dB,approximately 8dB BER performance improvement for the ABSR-based uncorrelated receiver when compared with the traditional uncorrelated receiver,in which SNR represents the ratio of BPAM signal power to background Laplacian noise power,i.e.,SNR(dB)=10log10（A2/2λ2）.In essence,through the bistable system parameters self-adaptive adjustment according to the quantitative cooperative resonance matching relationship in different SNR conditions,the reception performance improvement of the ABSR-based uncorrelated receiver benefit greatly from the unique advantage of SR,i.e.,making use of characteristic of the energy transferring from the random noise to useful signal in nonlinear BSR system to achieve the goal of noise-assisted signal transmission.

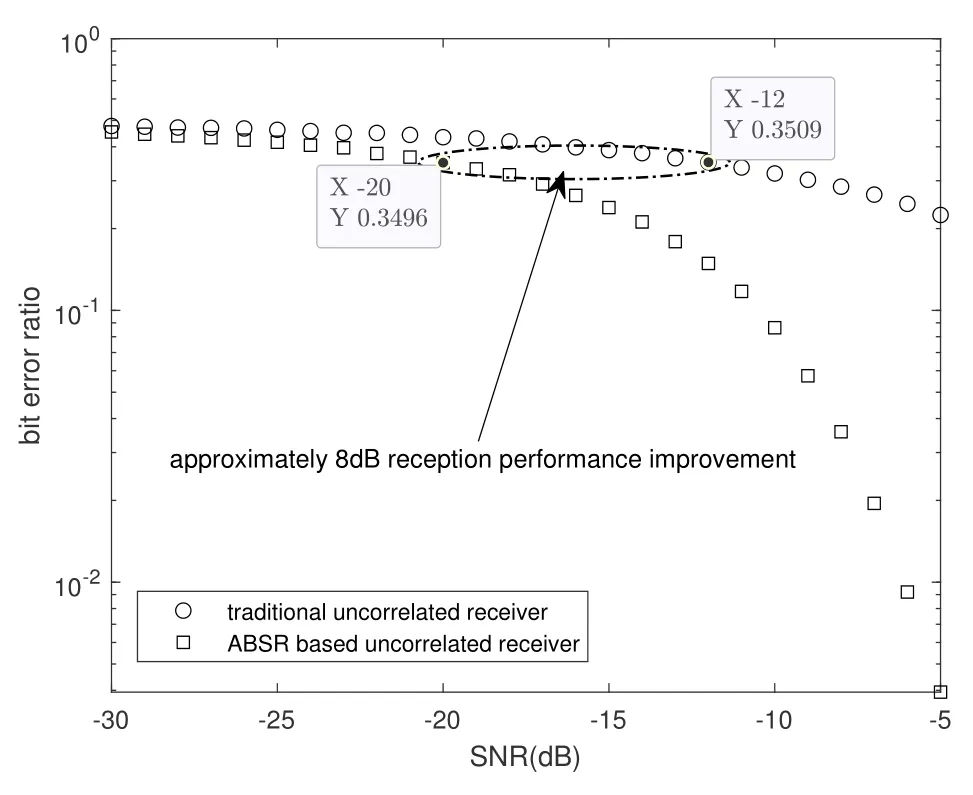
Figure 11. ABSR-based signal processing under Laplacian noise.

V.CONCLUSION

Based on the in-depth analysis of ASR principle under Gaussian white noise,this paper fully draws on the core idea of transfer learning,by analyzing the equivalent cooperative resonance effect under Gaussian white noise and Laplacian noise,the quantitative cooperative resonance matching relationship under Laplacian background noise is studied.On this basis,a novel weak signal reception scheme based on ABSR system is proposed,and the correctness and effectiveness of the proposed scheme is further evaluated by Monte Carlo simulations.Based on the research idea and method in this thesis,further exploration on cooperative resonance mechanism under other types of non-Gaussian noise,such as generalized Gaussian noise or α-stable distributed noise,will be a meaningful work in the future.

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation of China(62001356),in part by the National Natural Science Foundation for Distinguished Young Scholar (61825104),in part by the National Key Research and Development Program of China(2022YFC3301300)and in part by the Innovative Research Groups of the National Natural Science Foundation of China(62121001).