四元数亚正定系统混参分裂迭代方法

张燕婷, 黄敬频

(广西民族大学数学与物理学院, 南宁 530006)

大型结构矩阵方程问题广泛出现在科学与工程领域中,如固体力学、流体力学、最优化问题和鞍点问题都需要对大型线性系统进行求解[1-5]。在一般情况下,方程组的系数矩阵较为庞大,且有稀疏性,因此更适合对其进行迭代求解。多年来,许多学者针对不同结构的复系统进行过深入研究,形成较为丰富的研究成果。Bai等[6]于2003年对复亚正定系统首次提出了Hermitian 和斜Hermitian分裂迭代方法(Hermitian and skew-Hermitian splitting,HSS),该方法将系数矩阵A进行了Hermitian 和反Hermitian分裂(Hermitian and skew-Hermitian,HS),使得迭代具有格式对称、收敛速度快且无条件收敛等特点。此后,一些学者针对HSS迭代方法开展了一系列研究[7-9]。Li等[10]基于HS分裂,提出了非对称Hermitian 和斜Hermitian分裂迭代方法(asymmetric Hermitian and skew-Hermitian splitting,AHSS),并证明了该方法的收敛因子的上界取决于两个参数的选择、Hermitian部分H的谱、以及斜自共轭部分S的奇异值。初鲁等[11]提出了一类广义的非对称Hermitian 和斜Hermitian二步迭代(generalized lopsided Hermitian and skew-Hermitian splitting,GLHSS)迭代方法。文献[12]通过引入新参数并结合迭代松弛技术,提出一类外推的HSS迭代(extrapolation Hermitian and skew-Hermitian splitting,EHSS)。吴思婷等[13]将系数矩阵分解成正定矩阵和反Hermitian矩阵后进行非对称二步迭代,提出了外推的正定和反Hermitian方法(extrapolation positive definite and skew-Hermitian splitting,EPSS)。文献[14]对系数矩阵进行广义HS分裂,并结合外推技术,提出了外推的广义HSS迭代方法(extrapolation of generalized Hermitian and skew-Hermitian splitting,EGHSS)。文献[15]利用松弛迭代加速技巧,提出一种含有3个参数的超松弛迭代方法(successive over relaxation asymmetric Hermitian and skew-Hermitian splitting,SAHSS)。然而,这些成果均是针对复数域上的方程组进行讨论,缺少对大型结构四元数系统的迭代研究。

四元数是一种超复数,目前四元数在彩色图像恢复、量子物理、核滤波、自动控制与工程技术等领域发挥着越来越重要的作用[16]。因此,关于四元数矩阵方程的研究自然成为数值代数的热点课题。但由于四元数乘法的非交换原因,使得关于大型四元数系统的迭代研究尚鲜见报道[17]。鉴于此,针对四元数亚正定结构系统,运用松弛加速技巧,构建出新的混参分裂迭代方法,为解决实际问题提供理论基础。

1 ANPSS迭代构建

大规模线性方程组的求解,常常出现在科学与工程计算领域。在四元数体上考虑如式(1)所示的大型结构系统的迭代求解问题。

AX=B

(1)

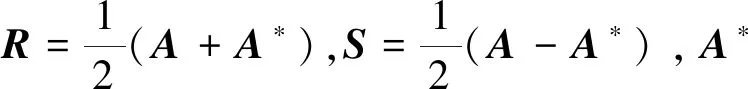
(2)

为提高NPSS迭代中参数选取的灵活性,引进新参数β>0,并构建如式(3)所示的迭代。

(3)

由式(3)中的第1个等式可得

X(k+1/2)=(αP+R)-1(αP-S)X(k)+
(αP+R)-1B

(4)

将式(4)代入式(3)中的第2个等式可得

X(k+1)=M(α,β)X(k)+N(α,β)

(5)

式(5)中:M(α,β)=(βP+S)-1(βP-R)(αP+R)-1(αP-S);N(α,β)=(βP+S)-1[(βP-R)(αP+R)-1+I],其中I为n阶单位矩阵。

于是迭代式(3)与式(5)等价。把式(5)称为非对称新自共轭正定和斜自共轭分裂迭代 (asymmetric new positive definite and skew-self-conjugate splitting,ANPSS),M(α,β)是其迭代矩阵。

2 ANPSS迭代收敛性

主要对ANPSS迭代进行收敛性分析,并给出收敛因子的上界。

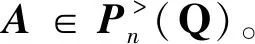
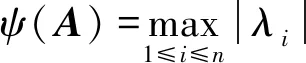
引理1[19]矩阵A∈Qn×n的谱值半径ψ(A)不超过其任意一种相容范数。特别地当A是正规矩阵时有ψ(A)=‖A‖2。

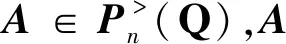
≜δ(α,β)

(6)

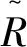
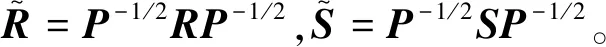
对式(5)中迭代矩阵M(α,β),其相似矩阵为

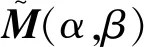
=P-1/2(βP+S)(βP+S)-1(βP-R)(αP+
R)-1(αP-S)(βP+S)-1P1/2

=P-1/2(βP-R)(αP+R)-1(αP-S)(βP+
S)-1P1/2

=(βI-P-1/2RP-1/2)(αI+P-1/2RP-1/2)-1(αI-
P-1/2SP-1/2)(βI+P-1/2SP-1/2)-1

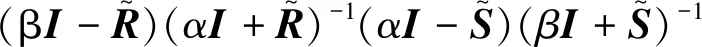
(7)

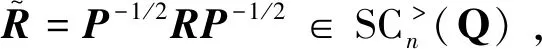
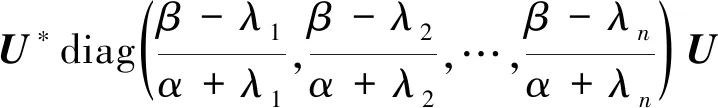
(8)

从而有

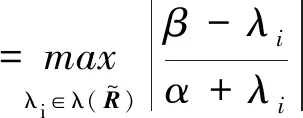
(9)

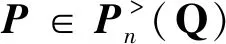
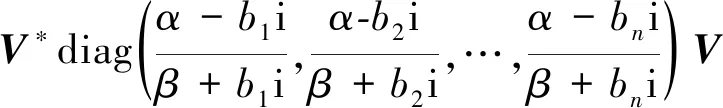
(10)

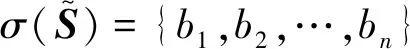
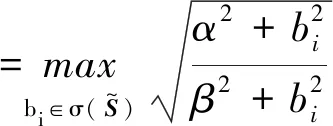
(11)

于是由式(7)、式(9)、式(11)可得

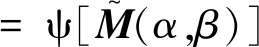
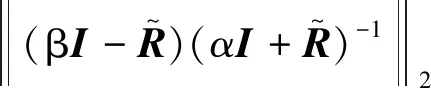
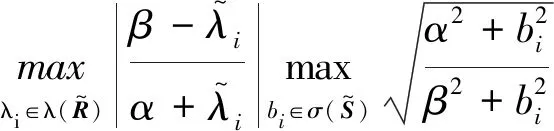
=δ(α,β)

(12)

证毕。

根据定理1中的上界δ(α,β),接下来给出ANPSS迭代的收敛条件。

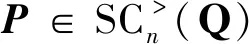
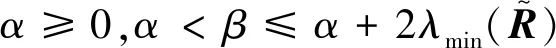
(13)

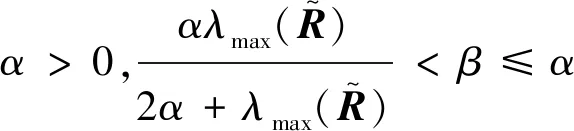
(14)

则ψ[M(α,β)]≤δ(α,β)<1,即ANPSS迭代收敛。

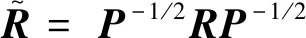
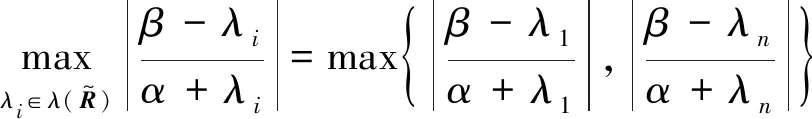
(15)

分两种情况讨论δ(α,β)的值。

(1)若β>α≥0,则由式(15)可知:

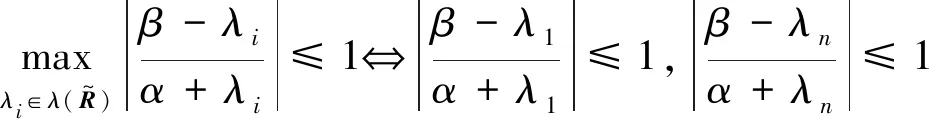
(16)

由式(16)的右边不等式组及β>α得

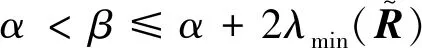
(17)

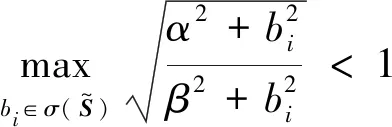
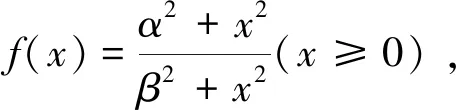
(18)

所以f(x)在[0,+∞)是单调减函数,其最大值为f(0),由此可得

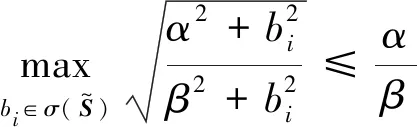
(19)

又根据式(12)可知,

(20)

由式(20)的右侧不等式组及0<β≤α解得

(21)

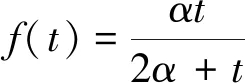
(22)

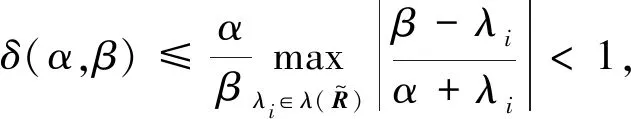
3 广义超松弛迭代

为进一步提高NPSS迭代的效率,运用松弛加速技术,构建一种新的求解四元数亚正定矩阵方程[式(1)]的混参分裂迭代方法。

首先,对式(3)中第一个等式进行变形,可得

RX(k+1/2)=(αP-S)X(k)-αPX(k+1/2)+B

(23)

将式(23)代入式(3)中第2个方程化简整理可得

(βP+S)X(k+1)=(S-αP)X(k)+(α+β)PX(k+1/2)

(24)

其次,通过引入松弛参数ω≥0来改进迭代序列式(24),即

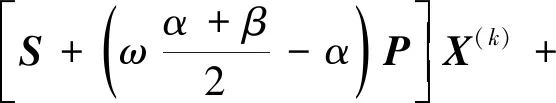
(25)

于是,联立ANPSS迭代式(3)中第1行等式和式(25)可得

(26)

式(26)中:α≥0,β>0,ω≥0为3个给定的参数。

显然,当ω=0时,式(25)即为式(24),迭代式(26)正是ANPSS迭代;当ω=0,α=β时,迭代式(26)退化为NPSS迭代方法[17]。

将式(26)等价地表示为

X(k+1)=M(α,β,ω)X(k)+N(α,β,ω)B,
k=0,1,…

(27)

式(27)中:

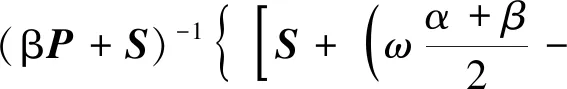
(28)

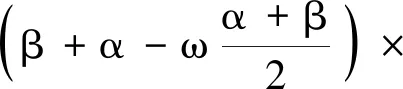
(29)

称迭代式(26)为超松弛非对称新自共轭正定和斜自共轭分裂迭代(successive over relaxation asymmetric new positive definite and skew-self-conjugate splitting,SANPSS),M(α,β,ω)是其迭代矩阵。

引理2ANPSS迭代式(5)的迭代矩阵M(α,β)与SANPSS迭代式(27)的迭代矩阵M(α,β,ω)的关系为

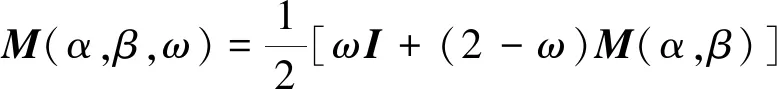
(30)

证明先对M(α,β,ω)变形运算可得

M(α,β,ω)

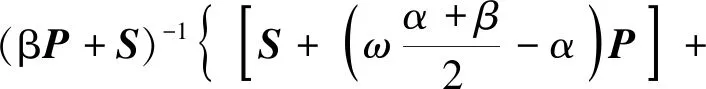
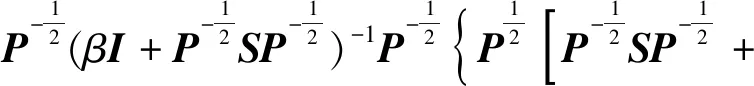
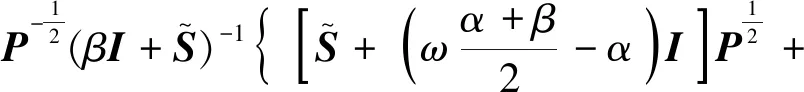
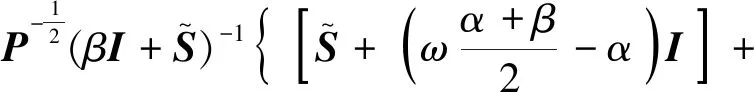
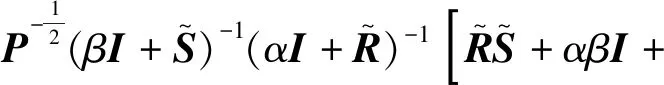
(31)

再对ωI+(2-ω)M(α,β)变形运算可得

ωI+(2-ω)M(α,β)

=ωI+(2-ω)(βP+S)-1(βP-R)(αP+
R)-1(αP-S)

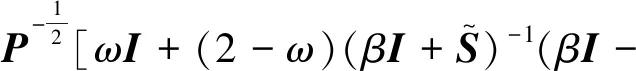
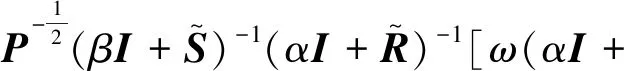
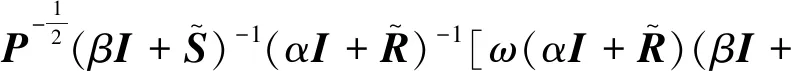
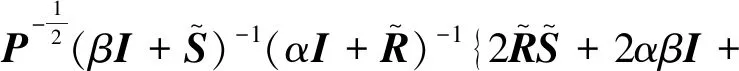
(32)

对比式(31)和式(32)可知,式(30)成立。证毕。

于是,关于SANPSS迭代的收敛性有如下结果。

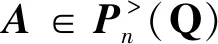
证明根据引理2有

(33)

设迭代矩阵M(α,β)、M(α,β,ω)的任意一个右特征主值分别为γj和μj,则由式(33)有

(34)

当ω≥0时,利用式(34)可得

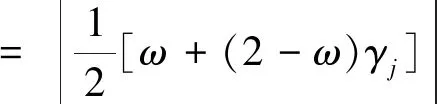
(35)

又根据定理1和式(35)有

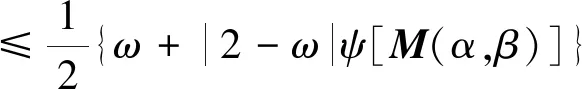
(36)

因此有

(37)

由式(37)可知,要使ψ[M(α,β,ω)]<1,只要不等式[式(38)]成立

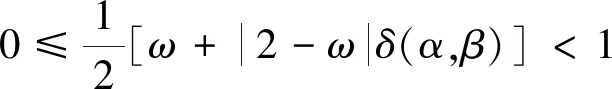
(38)

求解式(38)并结合ω≥0可得

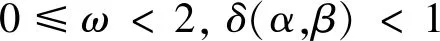
(39)

此时,再根据推论和式(39)可知,当条件①或②成立时,必有ψ[M(α,β,ω)]<1,证毕。

4 算法实现

设四元数矩阵X=X1+X2j∈Qm×n,记

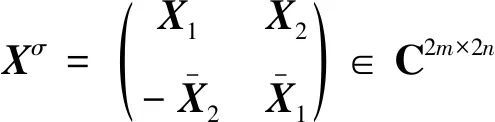
(40)

式(40)中:Xσ为X的复表示矩阵。

利用四元数矩阵的复表示及其运算性质,ANPSS迭代式(5)和SANPSS迭代式(27)均可转化成复数域C上等价的迭代,则有

(Xσ)(k+1)=[M(α,β)]σ(Xσ)(k)+
[N(α,β)]σ

(41)

(Xσ)(k+1)=[M(α,β,ω)]σ(Xσ)(k)+
[N(α,β,ω)]σ

(42)

式中:(·)σ为四元数矩阵(·)的复表示矩阵。

ANPSS迭代(5)和SANPSS迭代(27)分别给出M(α,β)、N(α,β)和M(α,β,ω)、N(α,β,ω)。

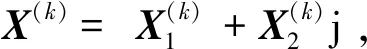
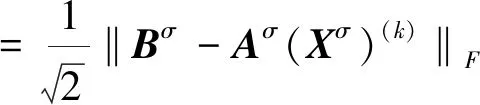
(43)

式(43)中:‖•‖F为F范数。

5 数值示例

对所提方法进行数值实验,并将ANPSS和SANPSS迭代与文献[17]中的NPSS迭代进行比较与分析,以检验所提方法的有效性。

假设迭代步数为IT,运算满足收敛要求所需时间记为CPU(以s为单位),矩阵的阶数为n,并选取初始迭代矩阵为单位矩阵,即X=I。

在数值实验中,所有的迭代实验都在个人计算机上的MATLAB(R2022a)中运行,并且当迭代误差ERR满足ERR<10-8或者迭代次数超过500次时终止。

示例1给定下列n阶矩阵,其中矩阵A是亚正定矩阵,矩阵B是四元数矩阵。

式中:A11=24-25k,A12=-3+12i-4j+6k,A21=-3+4i-14j-6k,A22=24-25k,A(n-1)n=-3+12i-4j+6k,An(n-1)=-3+4i-14j-6k,Ann=24-25k,i、j、k为虚数单位;

用SANPSS迭代求解式(1)。

解 首先求出矩阵A的自共轭分支R,斜自共轭分支S和矩阵B的复分解矩阵,即

R=R1+R2j,S=S1+S2j,B=B1+B2j

(44)

式(44)中:

其次选择自共轭正定矩阵P。

(45)

式(45)中:P12=1+3i+3j+3k,P21=1-3i-3j-3k,P(n-1)n=1+3i+3j+3k,Pn(n-1)=1-3i-3j-3k。

P的复分解矩阵为P=P1+P2j,其中,

分别利用文献[17]中的NPSS迭代方法和迭代格式[式(41)、式(42)]对方程组进行求解。其中,NPSS迭代中选取的α、ω满足文献[17]中的选取条件,ANPSS迭代所选取的α、β满足推论的条件[式(13)],SANPSS迭代中所选取的α、β、ω满足定理2的条件①,则对于不同阶数的矩阵,3种迭代方法的计算结果如表1～表3所示。

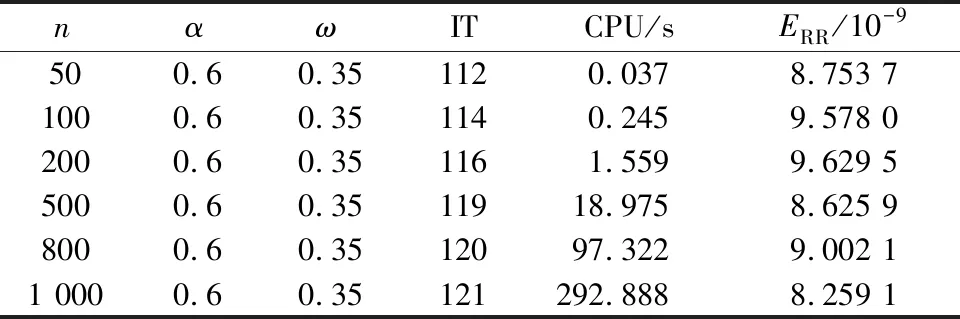
表1 NPSS方法不同阶数的迭代结果(示例1)Table 1 Iterative results of different orders of NPSS method(example 1)

表1、表2、表3分别为示例1中NPSS迭代、ANPSS迭代和SANPSS迭代的收敛次数、收敛时间以及迭代误差。表1和表2的实验结果表明,ANPSS迭代的收敛速度比NPSS迭代的收敛速度快。表2和表3的实验结果表明,当选择合适的参数时,SANPSS迭代比ANPSS迭代有较快的收敛速度,以及较少的迭代次数,即SANPSS迭代起到加速收敛的效果,效果如图1、图2所示。

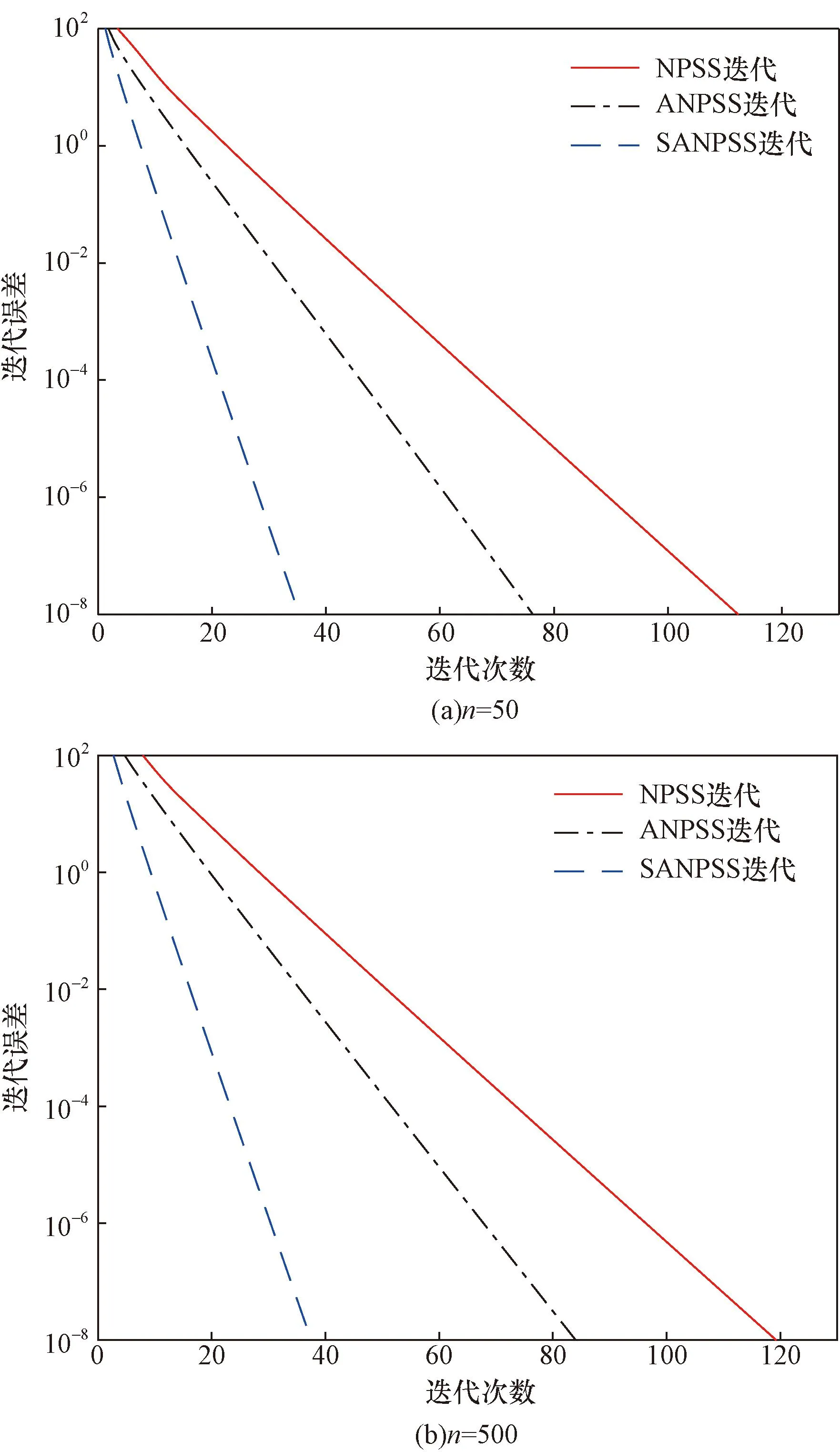
图1 当n=50、500时不同方法的迭代收敛情况(示例1)Fig.1 When n=50, 500 the iterative convergence diagram of different methods(example 1)

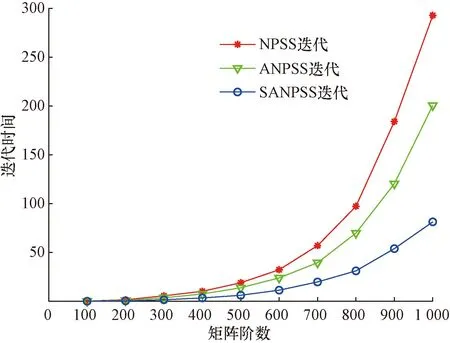
图2 不同矩阵阶数下NPSS、ANPSS、SANPSS方法的迭代时间对比(示例1)Fig.2 Comparison of iteration times of NPSS, ANPSS, and SANPSS methods under different matrix orders(example 1)

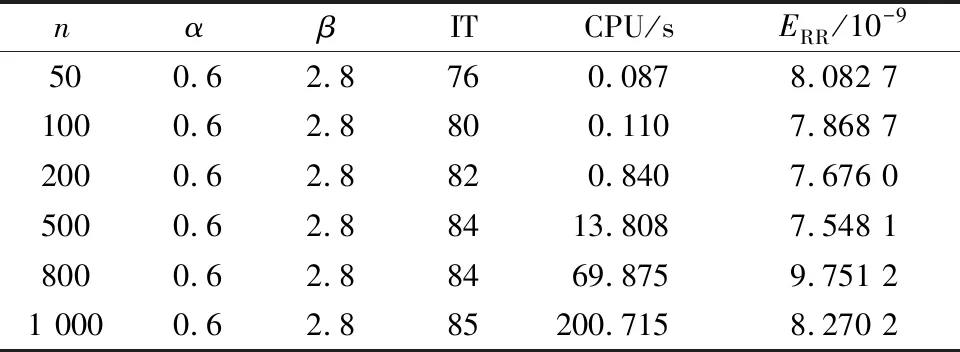
表2 ANPSS方法不同阶数的迭代结果(示例1)Table 2 Iterative results of different orders of ANPSS method(example 1)

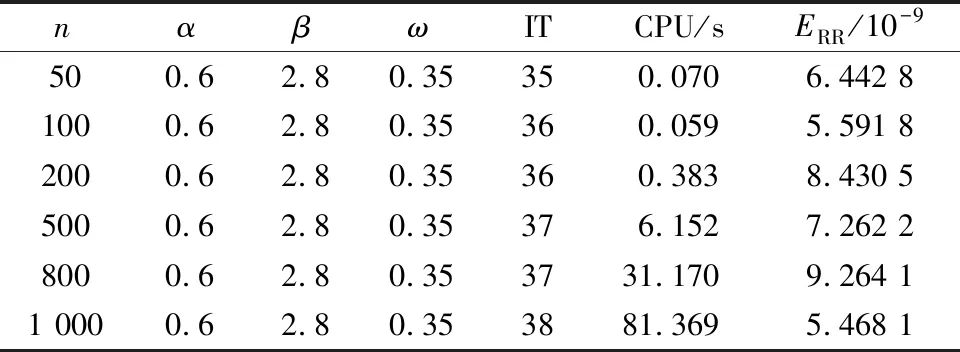
表3 SANPSS方法不同阶数的迭代结果(示例1)Table 3 Iterative results of different orders of SANPSS method(example 1)

图1(a)展示了示例1取n=50的情况下,NPSS迭代、ANPSS迭代和SANPSS迭代的迭代误差随着迭代次数的变化趋势。可以看出,SANPSS迭代方法的残差下降曲线位于NPSS迭代方法、ANPSS迭代方法的残差下降曲线之下。说明了SANPSS迭代比NPSS迭代、ANPSS迭代的迭代次数更少,迭代时间更短。图1(b)说明当系数矩阵的规模较大时,SANPSS迭代仍比NPSS迭代和ANPSS迭代都有更高的收敛效率。

图2展示了示例1在不同矩阵阶数的情况下,NPSS方法、ANPSS方法和SANPSS方法的迭代时间变化趋势图。可以看出,随着矩阵阶数变大,SANPSS迭代比NPSS迭代、ANPSS迭代所需时间更短,对比更明显。

示例2考虑如下大型结构系统的迭代求解问题,其中矩阵A是亚正定矩阵,矩阵B是四元数矩阵。

式中:A11=16.5+5i,A12=-1+2j,A21=-1-2i-2.4k,A22=16.5+5i,A(n-1)n=-1+2j,An(n-1)=-1-2i-2.4k,Ann=16.5+5i;

用SANPSS迭代求解。

解 先求出矩阵A的自共轭分支R,斜自共轭分支S和矩阵B的复分解矩阵,即

其次,选择自共轭正定矩阵P。

式中:P12=0.8+3i+3j+3k,P21=0.8-3i-3j-3k,P(n-1)n=0.8+3i+3j+3k,Pn(n-1)=0.8-3i-3j-3k。

其复分解矩阵为

分别利用文献[17]中的NPSS方法和迭代格式[式(41)、式(42)]求解方程组。其中,NPSS迭代中选取的α,ω满足文献[17]中的选取条件,ANPSS迭代所选取的α、β满足推论的条件[式(14)], SANPSS迭代方法中所选取的α、β、ω满足定理2的条件②。则对于不同阶数的矩阵,3种迭代方法的计算结果如表4～表6所示。

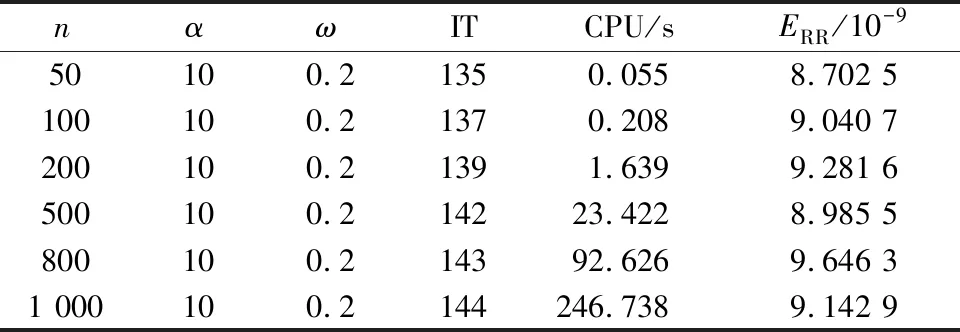
表4 NPSS方法不同阶数的迭代结果(示例2)Table 4 Iterative results of different orders of NPSS method(example 2)

表4～表6分别给出示例2中不同矩阵阶数下,NPSS迭代、ANPSS迭代和SANPSS迭代的收敛次数、收敛时间以及迭代误差。表4和表5的实验结果显示,ANPSS的收敛速度比NPSS的收敛速度快。表5和表6的实验结果表明,当选择合适的参数时,SANPSS迭代比ANPSS迭代收敛速度快,迭代次数也较少,即也说明SANPSS迭代起到了加速收敛的作用。效果如图3、图4所示。

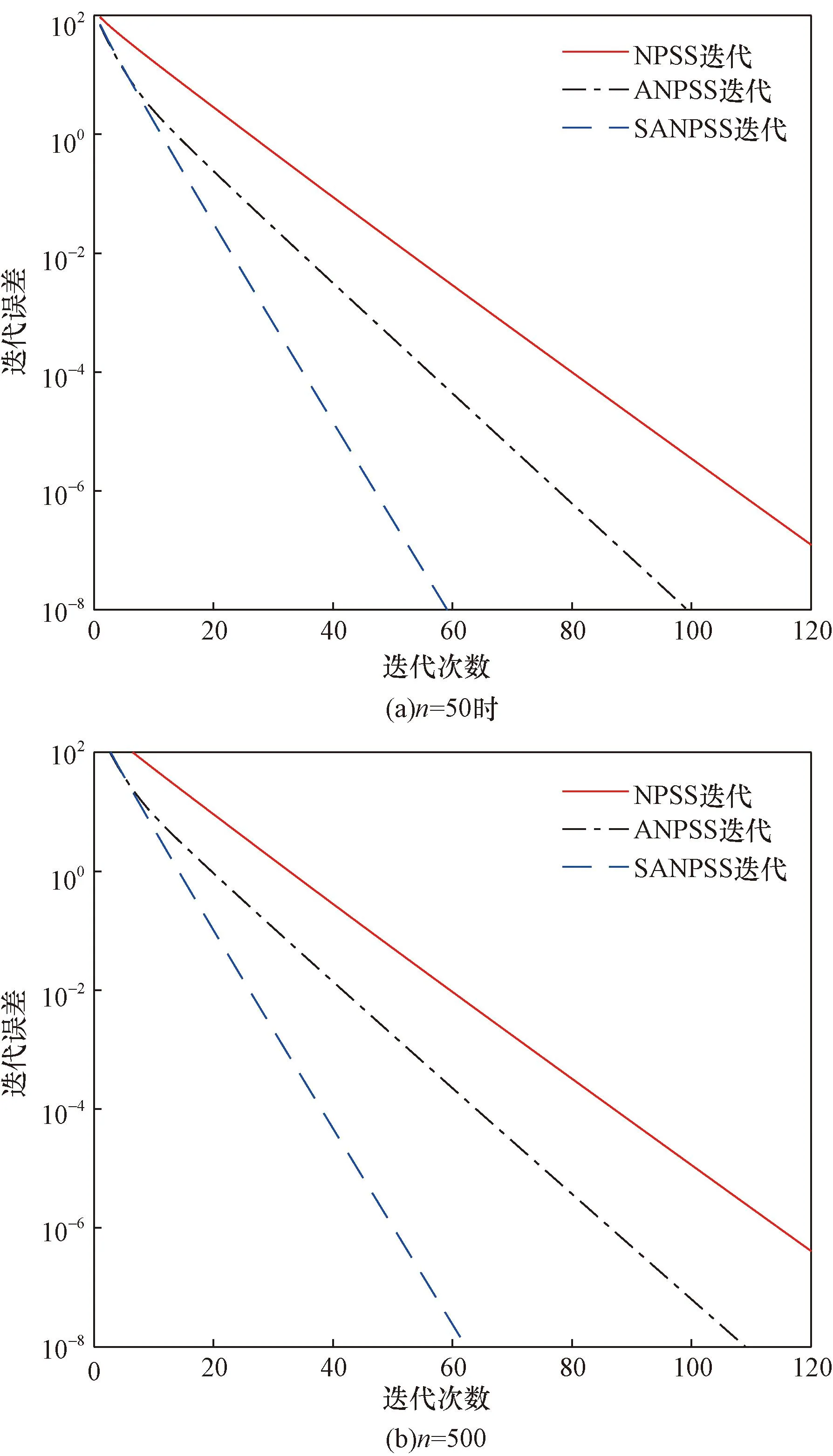
图3 当n=50、500时NPSS、ANPSS、SANPSS方法的迭代收敛情况图(示例2)Fig.3 When n=50, 500, iterative convergence of NPSS, ANPSS, SANPSS methods(example 2)

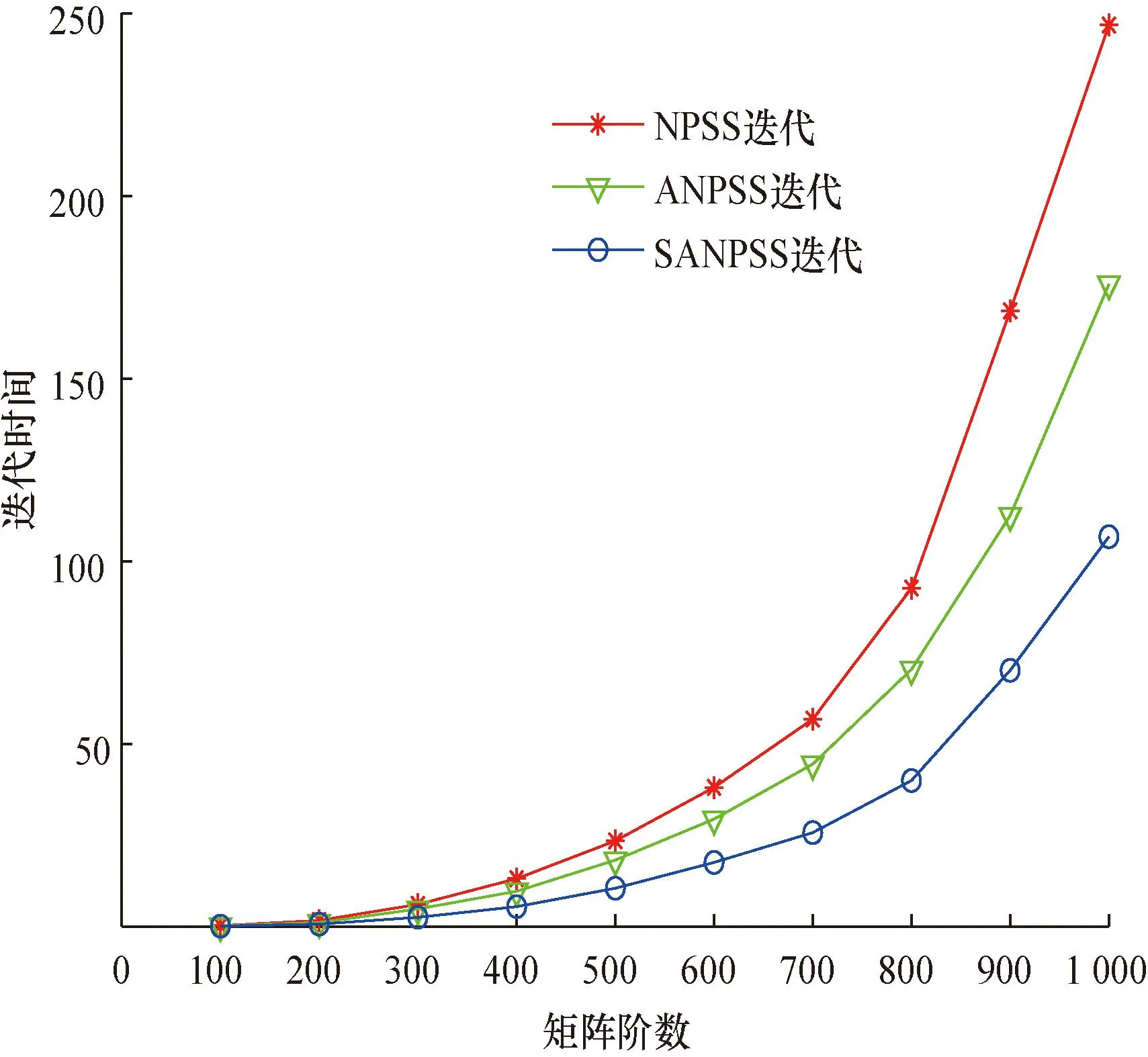
图4 不同矩阵阶数下NPSS、ANPSS、SANPSS方法的迭代时间对比(示例2)Fig.4 Comparison of iteration times of NPSS, ANPSS, and SANPSS methods under different matrix orders(example 2)

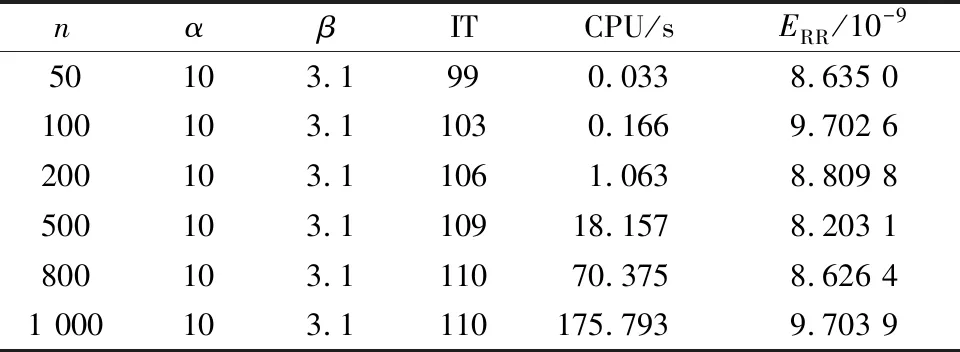
表5 ANPSS方法不同阶数的迭代结果(示例2)Table 5 Iterative results of different orders of ANPSS method(example 2)

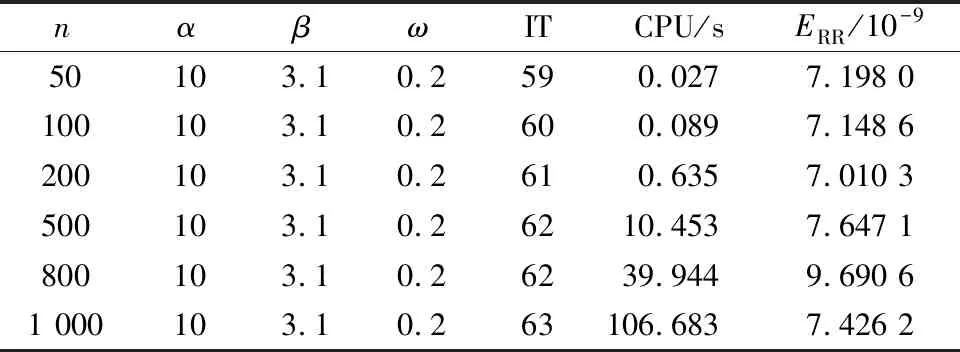
表6 SANPSS方法不同阶数的迭代结果(示例2)Table 6 Iterative results of different orders of SANPSS method(example 2)

在图3(a)、图3(b)中,SANPSS迭代方法的迭代收敛曲线位于NPSS迭代方法、ANPSS迭代方法的迭代收敛曲线之下,即说明SANPSS迭代方法在计算上所需迭代次数更少,所用时间更短。同时,通过对比图3(a)和图3(b)可知,当矩阵阶数较大时,SANPSS迭代方法展现的优势更明显。

从图4可以看出,SANPSS迭代方法的迭代时间曲线位于NPSS迭代方法、ANPSS迭代方法的迭代时间曲线之下。说明随着矩阵阶数的不断增大,SANPSS迭代比NPSS迭代、ANPSS迭代所需的迭代时间更短。

综合示例1和示例2,当满足定理2的条件①或条件②时,选择适当的α、β、ω参数,SANPSS迭代有一定程度的改进效果。

6 结论

讨论四元数亚正定系统的混参分裂迭代求解问题。首先,在NPSS迭代基础上,通过引入新的参数,构建出双参ANPSS迭代,然后运用四元数矩阵特征值理论,获得该迭代收敛的参数选取方法。同时利用超松弛加速技术,提出了混参SANPSS迭代,并讨论该迭代与ANPSS迭代的关联性,从而获得其参数选取方法。运用四元数矩阵的复表示,在MATLAB环境下实现方程的求解。数值算例表明,当选择适当的参数时,SANPSS迭代比ANPSS具有更高的收敛效率。所提的ANPSS迭代和SANPSS迭代均较大程度改进了相关文献的结果。