基于加州承载比试验的隧道弃渣颗粒接触力场形状影响因素分析

岳夏冰, 丁同, 黄姣*, 王奕丁, 王学营, 江黎

(1.长安大学公路学院, 西安 710064; 2.内蒙古自治区交通运输科学发展研究院, 呼和浩特 010051;3.生态安全屏障区交通网设施管控及循环修复技术交通运输行业重点实验室, 呼和浩特 010051;4.西安公路研究院有限公司, 西安710065)

近年来,中国公路、铁路发展快速,越来越多地质条件复杂的高山、丘陵等地区开始发展公路、铁路建设。由此产生的大量弃渣处置不当容易影响沿线生态环境和工程安全,同时公路、铁路建设又需要大量的建筑材料,目前将隧道弃渣用于工程的研究已日益有所成效[1-2]。这些弃渣主要应用于路基填筑、路基防护工程、机制砂以及隧道工程。

研究表明,隧道弃渣破碎加工后的级配碎石作路基的填筑材料能够有效改善路基承载性能,提高其稳定性[3-4]。级配碎石用作路基填料可以为面层提供均匀且稳定的支撑,将交通荷载传递且减轻给地基土。在冻土地区,碎石路基填料可以通过其孔隙间的空气对流对路基进行降温更好保护冻土[5-6],水泥稳定碎石填料能有效减小路基的冻胀变形[7]。王青志等[8]进行室内封闭系统冻胀正交试验研究级配碎石的冻胀特性,发现影响级配碎石冻胀率的主要因素是含水率。在级配碎石变形特性研究方面,杨志浩等[9]将试验与理论结合提出考虑应力水平及细粒含量参数的塑性蠕变动力行为累积塑性应变预测模型。黄永发等[10]利用颗粒流程序构建矿区道路细观结构研究了结构内部颗粒接触力、位移变化情况。张欣等[11]研发智慧集料传感系统结合三轴剪切试验进行分析验证。Du等[12]进行全应力-应变曲线试验,建立再生骨料混凝土(RAC)应力-应变本构模型研究其力学性能。Hu等[13]针对级配碎石材料的组成结构,利用颗粒流分析软件PFC3D构建试验模型为级配碎石细观力学状态的研究和物理力学试验提供依据。刘宝等[14]为研究不同含水状态下基床级配碎石填料变形特性开展大型静动三轴试验,建立累积应变预测模型。岳爱军等[15]通过多个试验研究低掺量水泥对级配碎石力学性能的影响并建立相关模型预测。吕松涛等[16]采用分层铺筑与反挖的形式研究级配碎石结构层在不同应力状态下的模量特性,发现反挖方法与实际服役条件较为相符。对于颗粒形状影响的研究,近几年来主要包括扫描分析、试验以及数值模拟。孙壮壮等[17]通过扫描、形状分析和单颗粒压缩试验分析表明破碎强度均存在明显的尺寸效应。陆瑞等[18]采用激光扫描仪研究高速铁路路基级配碎石颗粒形态,其成果为从宏、中、细观3个尺度量化评价颗粒形态特征提供参考。索智等[19]通过级配检验、试验路弯沉测试、雷达扫描和压实度检测,发现超大粒径级配碎石构成了结构、力学指标优于骨架型、连续型级配碎石,并且其作为沥青路面基层,具有强度高、连续性好、密实均匀的优点。周海娟等[20]采用连续离散耦合分析方法再现了破碎强度随着颗粒尺寸的增大而逐渐减小。张翀等[21]研究了颗粒形状对模拟双轴试验的影响得出不同颗粒试样宏观特性与细观参数的变化规律均比较一致。

研究表明,颗粒的形状对于集料整体力学性质有着很大的影响,随着颗粒形状的变化,颗粒之间嵌挤和摩擦均会出现明显变化,进而有不同的整体强度[22-24]。对级配碎石而言,不同的颗粒表面性质也会影响其颗粒接触力场形状、大小及梯度,进而改变其所受的约束力。然而,目前隧道弃渣制成的级配碎石颗粒细观参数与其颗粒接触力场及约束力之间的影响关系尚不明确,各参数对接触力场的作用机理研究较少。鉴于此,借助PFC3D对加州承载比(California bearing ratio,CBR)试验进行模拟,研究CBR试验全过程中隧道弃渣制的级配碎石颗粒运动轨迹及受力情况,并对试样中颗粒接触力的传递进行分析,确定其作用机理。

1 CBR试验模型初始设定及构建

1.1 CBR试验及模型选择

依托实际高速公路隧道洞渣加工再利用项目,对填筑路面基层所使用的级配碎石展开细观力学性能研究。对现场取样进行筛分并参考文献[25]进行级配优化,优化后的级配如表1所示。随后进行CBR试验,为后续模拟试验提供数据支持及参照。

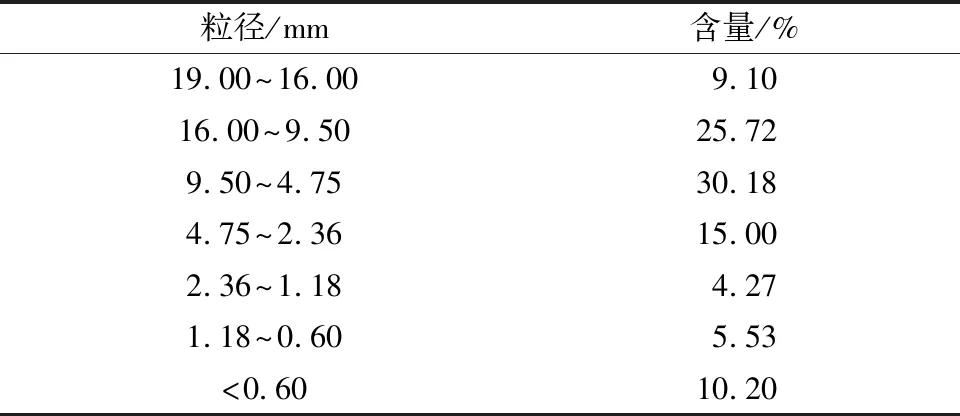
表1 室内试验级配Table 1 Test grading indoor

CBR试验具有设备简单、操作便捷、数据易处理等优点,通过试验所得的CBR值可直观表征散体压实材料的竖向刚度及抗剪切能力,以此反映路基承载能力。试验CBR值一般取贯入量为2.5 mm时的单位压力与标准荷载强度的比值,但同时应对比贯入量为5.0 mm时的CBR值,参考《公路土工试验规程》(JTG 3430—2020)[26]最终确定CBR值。

考虑实际碎石个体形状复杂性,在模型建立过程中考虑调整了颗粒接触模型及相关参数,以实现颗粒形状对模拟结果的影响,同时利用转动阻力线性模型对颗粒接触中的法向力、切向力、摩擦力以及咬合力的影响进行模拟。

1.2 CBR模型设计

1.2.1 细观参数标定

考虑线性接触模型需确定的细观试验参数有孔隙率n、颗粒粒径区间比[Rmin,Rmax](Rmin、Rmax分别为最小、大颗粒粒径)、颗粒法向刚度kn、切向刚度ks、颗粒摩擦系数μ、法向临界阻尼比βn、切向临界阻尼比βs、法向黏结强度Tσ及切向黏结强度Sσ等,考虑转动阻力模型还需确定动阻力系数μr等转动相关参数,综合文献[24]以及CBR试验结果等最终确定颗粒细观参数,如表2所示。

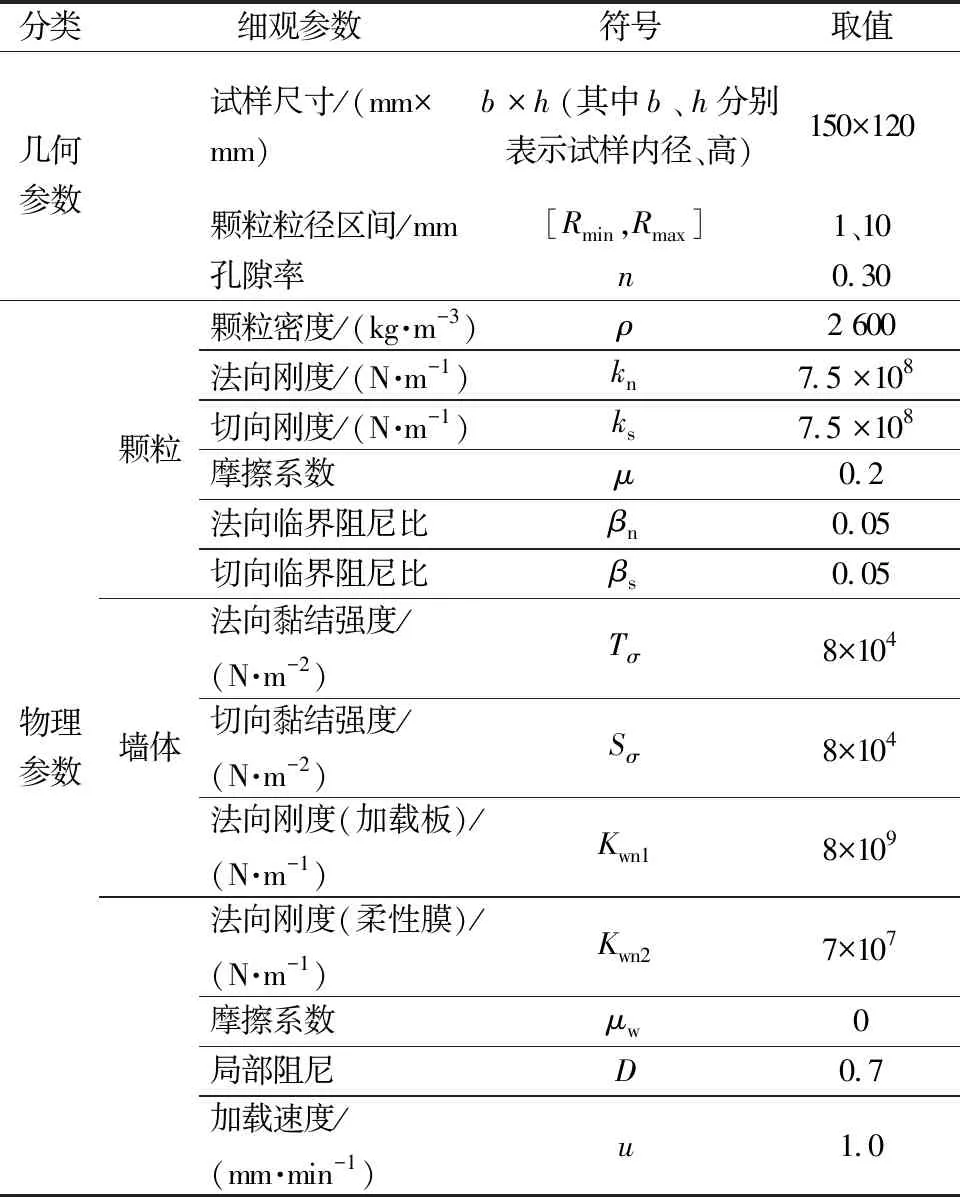
表2 颗粒细观参数Table 2 Particle mesoscopic parameters

1.2.2 CBR模型构建

参照表2颗粒细观参数设置CBR模型参数,根据室内CBR试验中试样的边界条件构建模型。压实前后的试样如图1所示。在设定范围内生成级配碎石颗粒,考虑重力作用下沉,其力链网络自上而下逐渐密集。自顶面墙体向下施加压力,当整个试件竖向被力链整体贯穿即为固结完毕。

相邻颗粒圆心的连线表示接触力链,其颜色及粗细表示大小不同的接触力图1 CBR试样模型固结前后对比Fig.1 Comparison of CBR sample model before and after consolidation

删除顶面墙体,设立1、2、3号墙体共同组成模拟压头,模拟压头即模拟CBR试验中的贯入杆,在其左右两侧的试样顶面各设置一荷载板,其宽度均为50 mm,如图2所示。实际试验中需要压载4块单块质量1.25 kg的荷载板,则4、5号墙体各需要对试样施加25 N的力。试验开始前在贯入杆上施加45 N荷载作为初始值。试验过程中4、5号墙体所受应力均保持不变,故需要利用伺服机制控制。

在试样边界加载情况达到试验要求后,对模拟压头赋予一恒定速度使其压入试样,选用1.25 mm/min作为贯入速度,贯入量增长至6 mm时停止加载。

为验证数值模拟的有效性,利用室内试验所得贯入力-贯入量曲线与模拟试验曲线进行对比,如图3所示。可以看出,两曲线的发展趋势较为吻合,表明通过选取合理的接触模型及细观参数,可利用颗粒流模型较好地对CBR试验进行数值模拟。由表3可知,室内试验与数值试验两者结果的偏差为5.33%,说明模拟试验的试验结果与真实情况相差不大,因此在此基础上开展的颗粒接触力场形状影响因素研究结果有效。

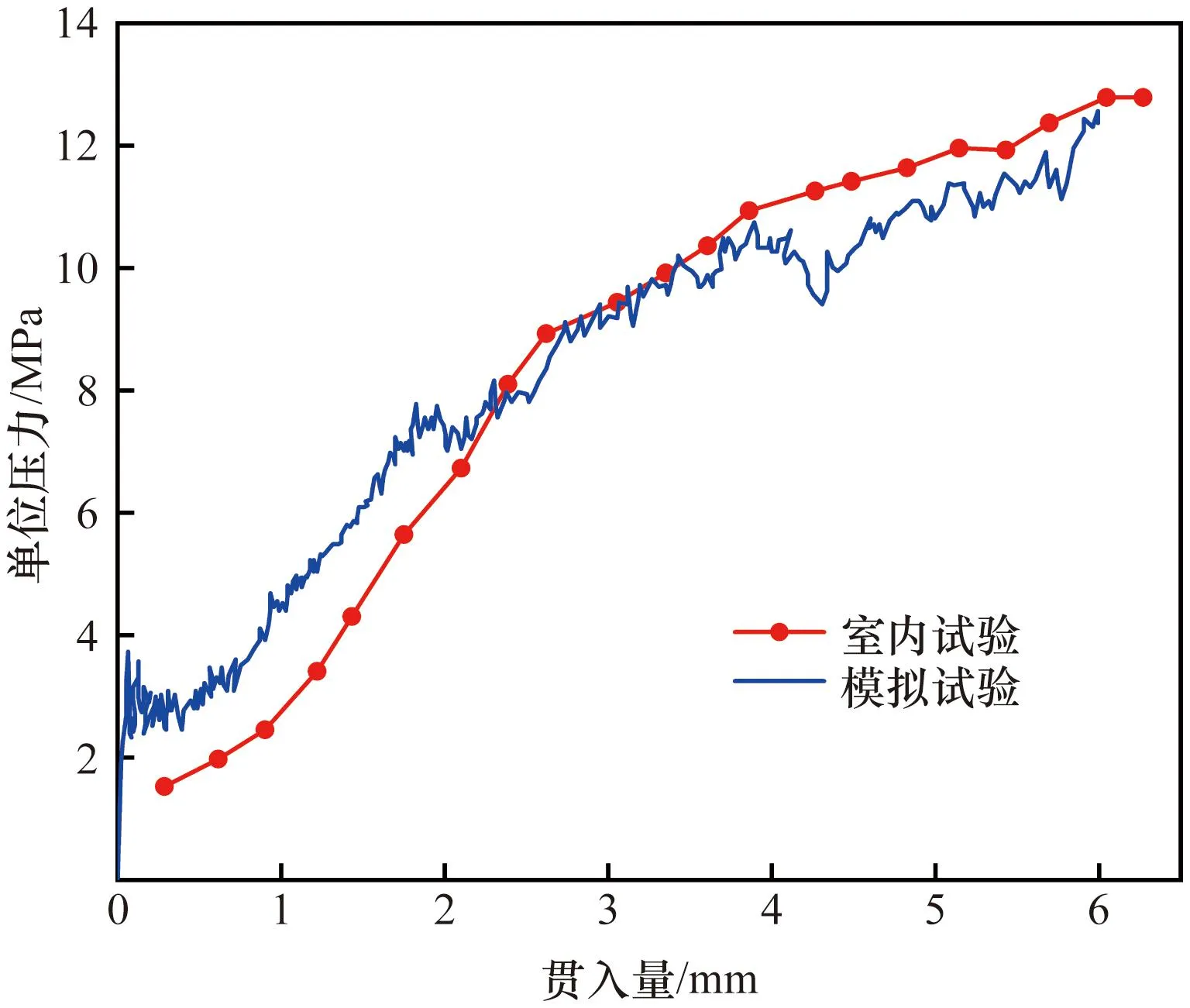
图3 室内试验及数值试验所得CBR曲线对比Fig.3 Comparison of CBR curves obtained from indoor test and numerical test

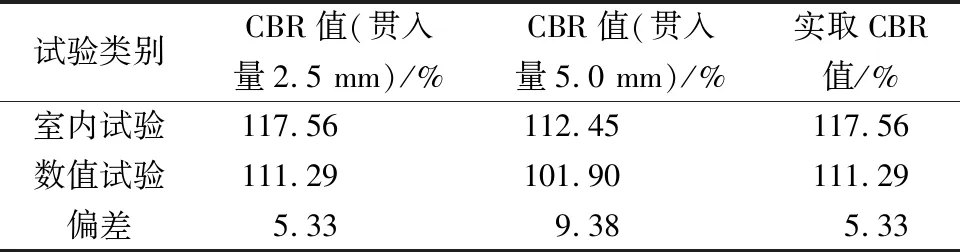
表3 室内试验及数值试验所得CBR值对比Table 3 Comparison of CBR values obtained from indoor test and numerical test

2 试样颗粒接触力场形状影响因素分析

2.1 CBR试验与谷仓效应

谷仓效应指谷仓中储存的谷物增加到一定高度后,谷仓底部受力便维持在一恒定值的现象。其原理为在侧向约束条件下,谷物间的摩擦力发生侧向扩散,其竖向分力与谷物所受重力达到平衡。该现象与颗粒及墙体的表面性质密切相关。

CBR试验中,试样所受到的约束环境与谷仓类似,但其上部并不靠增加试样高度来提升试样中颗粒竖向受力,而是借助贯入杆与加载板的竖向活动。加载板保证了试样上表面保持平整,而贯入行为可理解为不断增加高度的级配碎石对下部试样施加的重量。由于试样尺寸固定,颗粒与墙体接触面积有限。且调整墙体相关参数进行试验,经验证,墙体表面性质对CBR试验结果的影响不明显。故主要研究颗粒细观参数与谷仓效应的相关性。研究由侧板及底板所受法向力的演化过程展开,并对其比值变化进行分析。

试验过程中侧板与底板受力之比如图4所示,其中侧板接触力取两侧板受力的平均值。结合图3中的CBR曲线进行分析。贯入量达到0.2 mm前试样处于压实阶段,此时贯入导致的颗粒接触力场未触及试样边界,故侧板与底板受力之比无明显改变。在贯入进行至0.5 mm,侧板受力迅速提升,使曲线达到一明显峰值,试样此时处于弹性阶段。该峰值反映了贯入行为使试样颗粒明显向两侧排挤的现象,水平向力链由此在试样上部扩展。而后由于贯入行为的持续进行,颗粒接触键开始大量发生切向破坏,颗粒产生向下的位移,试样竖向被力链贯穿,使贯入力直接传导至底板,故峰值迅速回落。而后曲线呈抛物线形状上升,表示侧向约束受力的增长速度较大。由于侧板与底板受力比值始终小于1,故试样整体仍以竖向挤压为主。

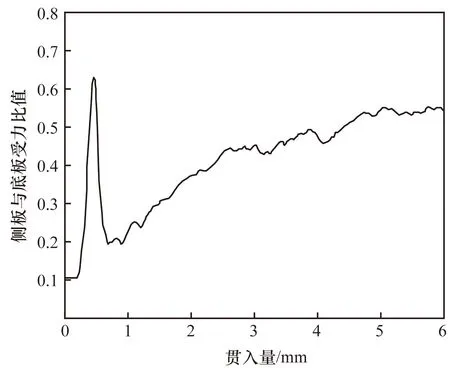
图4 试样筒侧板与底板所受法向力比值演变Fig.4 Evolution of normal force ratio between side plate and bottom plate of sample cylinder

2.2 颗粒刚度比

同调整刚度比所得到的CBR值无明显变化类似,颗粒刚度比对试样边界受力的影响并不显著,如图5所示。各受力曲线离散性较小,进一步表明颗粒法向刚度对接触力场的形状无明显调节作用。

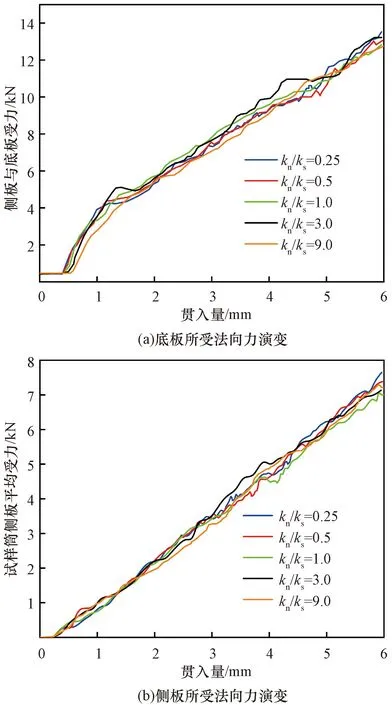
图5 不同kn/ks对应试样边界所受法向力的演变Fig.5 Evolution of normal force on sample boundary corresponding to different kn/ks

图6展示了侧板与底板受力比值随刚度比的变化趋势。随着kn/ks的增大,比值先减小后增大。在kn/ks<6时,贯入力在试件竖向作用较大,底板接触力随法向刚度增加发生正向增长,侧板受力的增速明显小于底板。而kn/ks>6时,侧板受力增速扩大,试样中接触力场的侧向范围和梯度增长速度明显增大。随法向刚度增长,试样整体颗粒的法向可压缩量明显减小,导致侧板受力随kn/ks增大而增大。kn/ks<6时,试样底部压实体的竖向承载力随kn/ks的增大不断增长,试样的剪胀效应愈加不明显。kn/ks>6时,试样竖向压实已到达极限,试样径向尺寸增大的趋势愈加明显。此时颗粒法向对接触力作用的敏感性减弱,即应变量减小,导致颗粒接触键更倾向于发生切向破坏;与颗粒法向难以变形相互叠加,使得试样底部的锥状压实体与试样上部之间形成明显滑移面。随法向刚度增大该现象愈加明显,其起到了分流竖向力以将部分竖向力转化为水平向力的作用,由此侧板与底板受力的比值得以迅速增长。

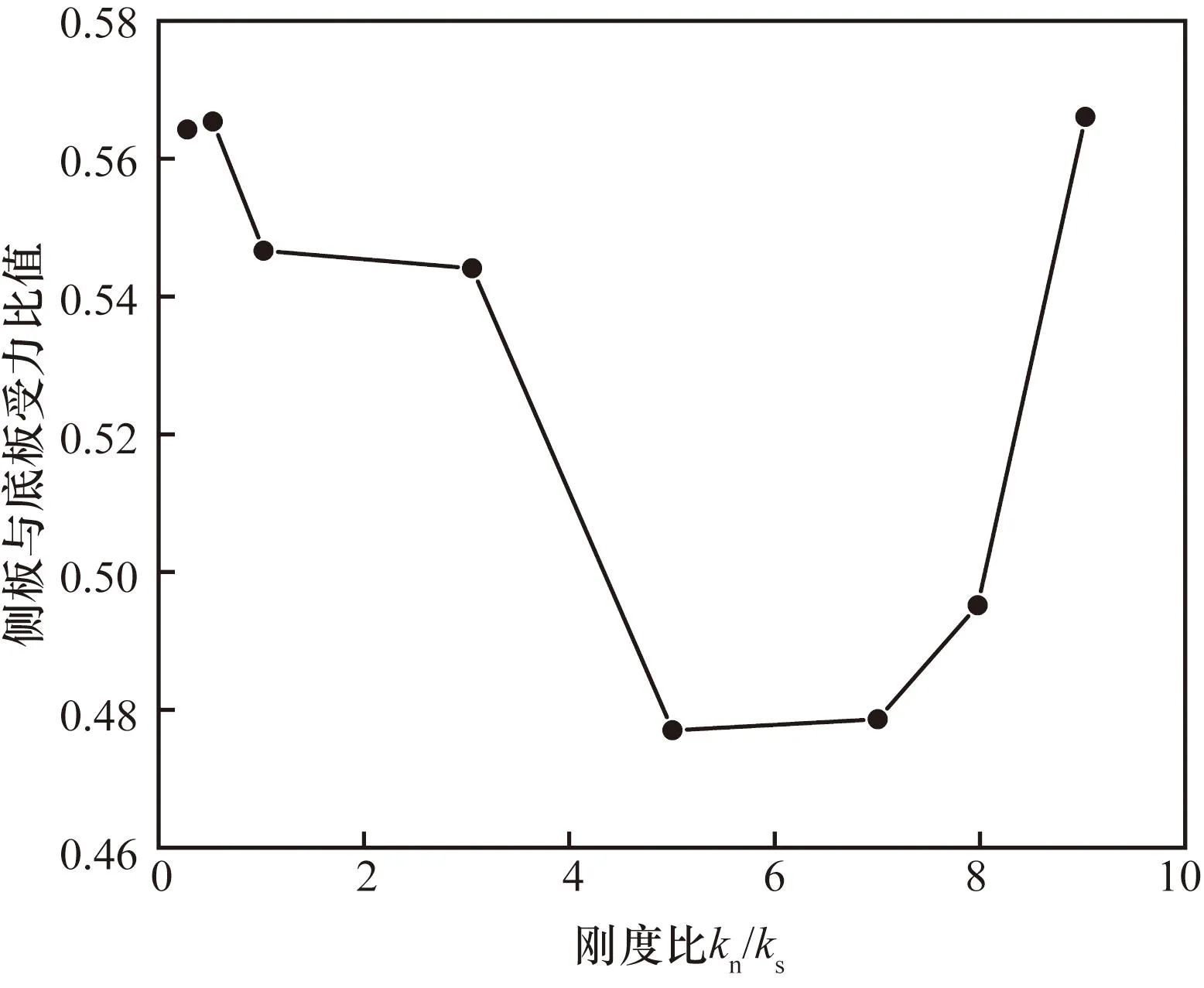
图6 试样筒侧板与底板所受法向力比值随kn/ks的变化Fig.6 Change of the ratio of normal force on the side plate and bottom plate of the sample cylinder with kn/ks

2.3 颗粒摩擦系数

由图7可知,不同摩擦系数μ对应的底板及侧板受力曲线变化较为明显,各曲线斜率绝对值随摩擦系数正向增长。且侧板受力曲线按斜率可分为两组,摩擦系数0和0.2所对应曲线较为接近,其他变量组走势较为相似,应为此区间内摩擦系数对侧板受力影响为非线性关系导致。

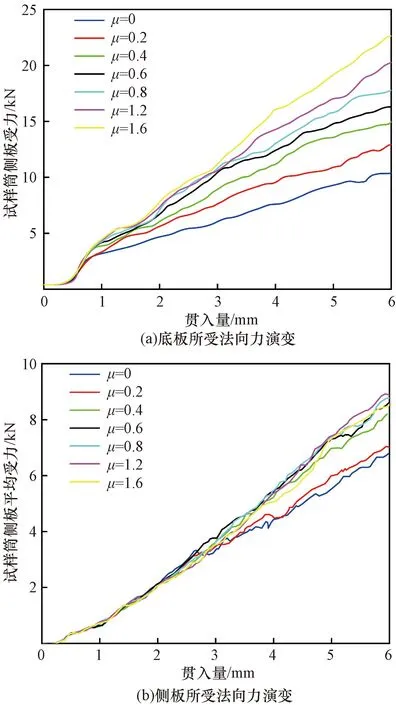
图7 不同μ对应试样边界受力的演变Fig.7 Evolution of stress on the boundary of samples corresponding to different μ

由墙体受力比值曲线(图8)可知,其可用斜率为负的线性函数拟合,表明μ对试件约束墙体受力影响较大,且两者呈线性相关。其原因为μ对接触键切向力学行为起阻碍作用,该作用强度与μ呈线性正相关,且μ的有效作用范围较广。该曲线展示出,随μ增加,试样接触力场的形状偏向竖直发展,竖向长细比线性增长。细观层面上,μ增大会使贯入力对颗粒所做的功更大地损耗于动摩擦行为中,从而改变接触力场的影响范围及梯度值。μ=0时,颗粒发生动摩擦不消耗其动能,颗粒发生位移后可将其全部动能施加在相接触颗粒上,由此生成力链的传导效率处于理想状态。试样底部压实体与其余部分发生滑移时,上部颗粒可将其动能沿滑移面向侧板传递,μ=0时颗粒动能最大,此时侧板与底板接触力之比最为接近1。而当μ较大时,颗粒间动摩擦阶段需消耗动能,由于摩擦力作用产生的颗粒转动也会消耗部分能量,致使贯入力在颗粒运动过程所做的功相对增加,进一步增大相同贯入量对试样发生变形所施加的能量。故随着μ的增大,试样趋于在竖向加强整体性,而逐渐弱于发生需进行大规模动摩擦行为才可形成的试样剪胀。

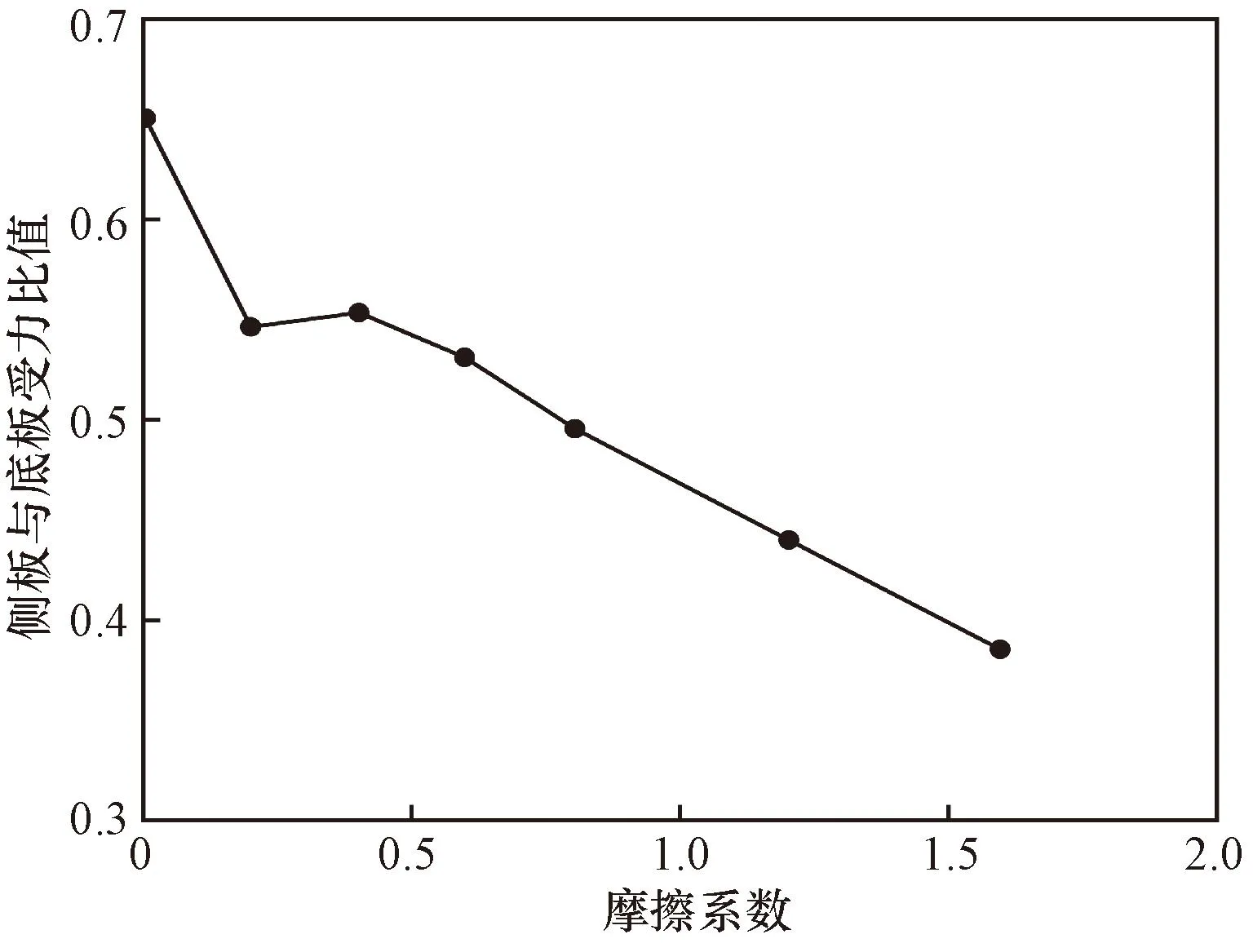
图8 试样筒侧板与底板所受法向力比值随μ的变化Fig.8 Change of normal force ratio between side plate and bottom plate of sample cylinder withμ

2.4 颗粒黏结强度

设定Tσ/Sσ=1,颗粒黏结强度对底部边界与侧面边界接触力的影响如图9所示,受力曲线斜率绝对值随黏结强度正向增长,而对侧板接触力,黏结强度较大时相应曲线出现了较大波动,不再以恒定斜率均匀增长,其斜率也出现下降趋势。此时试样展现出较大黏性,对颗粒接触键的破裂起阻碍作用,为颗粒发生侧向位移增加了难度。

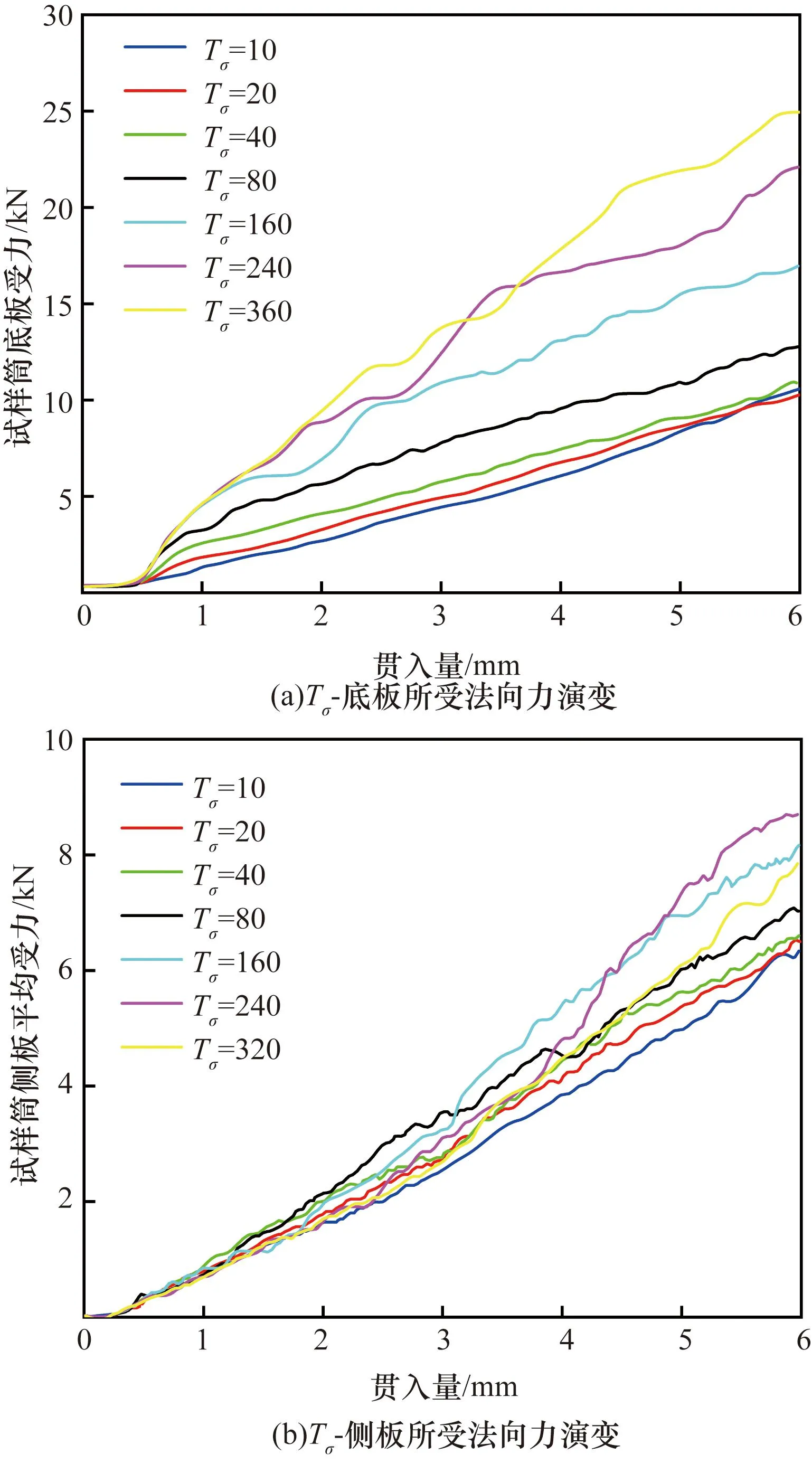
图9 不同Tσ对应试样边界受力的演变Fig.9 Evolution of stress on the boundary of samples corresponding to different Tσ

与摩擦系数类似,黏结强度影响下的受力比值曲线可描述为一斜率为负的直线段,如图10所示。表明Tσ/Sσ=1时,随黏结强度增大,接触力场范围的长细比线性增大。黏结强度较小时,接触键受到较

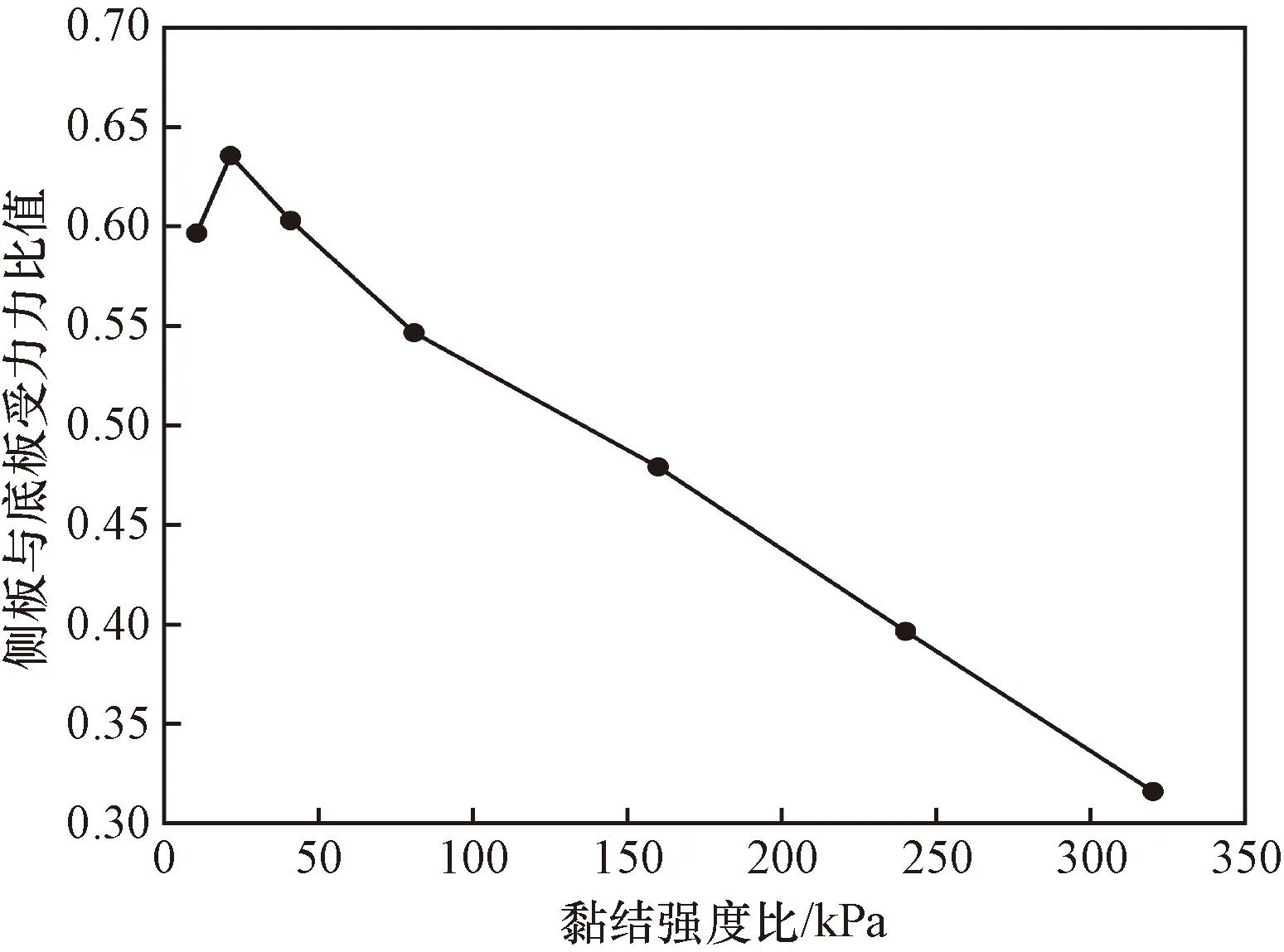
图10 试样筒侧板与底板所受法向力比值随Tσ的变化Fig.10 Change of normal force ratio between side plate and bottom plate of sample cylinder with Tσ

小的力或力矩便可发生破坏,试样整体接近散体状态,此时试样接触力场的形状最为接近圆形,表现为侧板与底板受力比值最为接近1。随着黏结强度的增长,颗粒接触键的法向及切向的黏滞性逐渐增加,大量形成的黏结基团提高了试样的整体性,加强了力链竖向分量的发展。

2.5 颗粒黏结强度比

由于黏结强度比中法向及切向参数在颗粒相对运动中所起的作用不同,故分别分析。切向参数不变,仅改变法向黏结强度的各Tσ/Sσ对应的边界所受接触力曲线如图11所示。可以看出,各曲线斜率基本相同,且各曲线的离散程度较小。表明法向黏结强度对试样接触力场形状的影响较小。

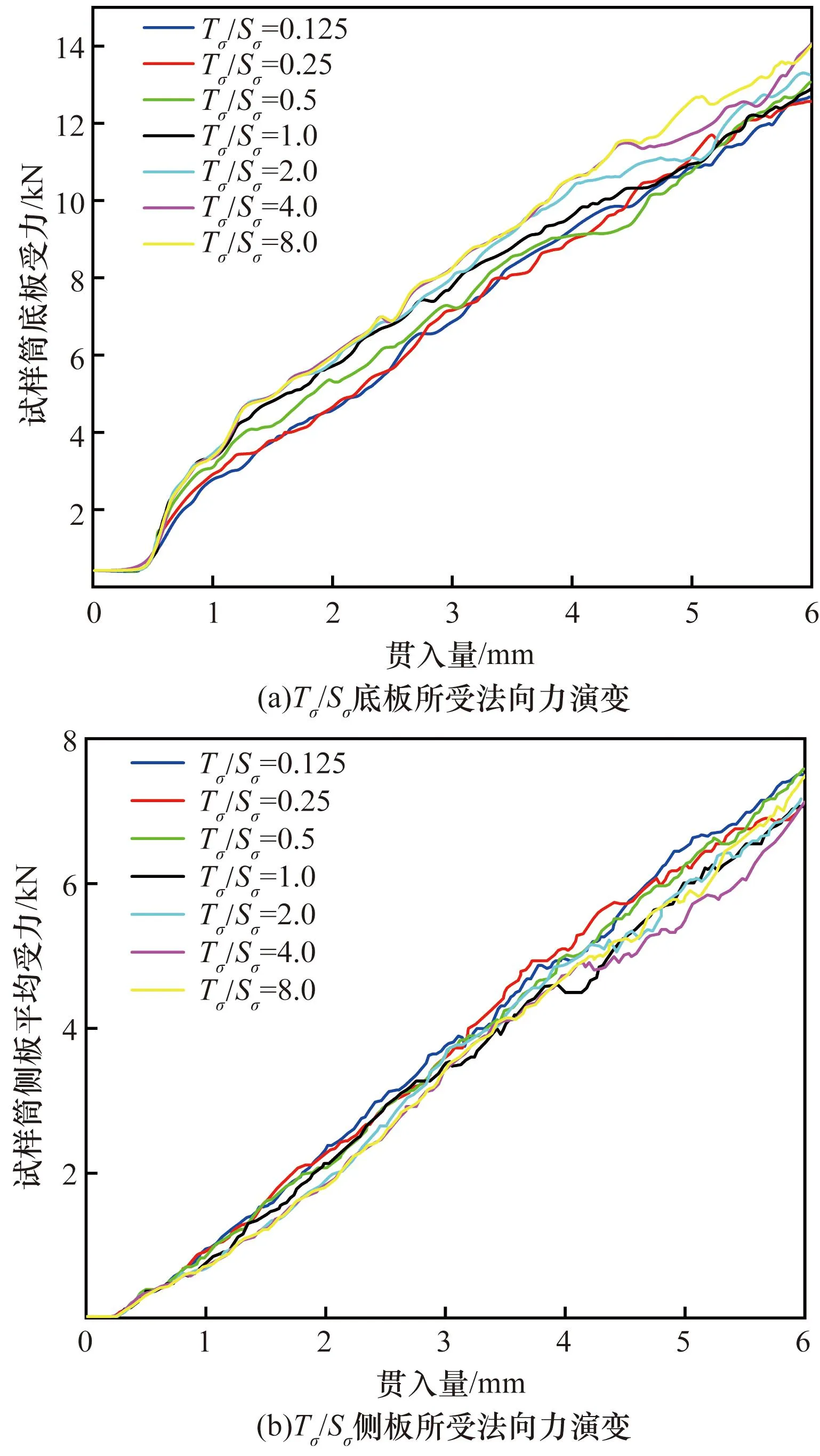
图11 不同Tσ/Sσ(Sσ不变)对应试样边界受力的演变Fig.11 Evolution of stress on the boundary of samples corresponding to different Tσ/Sσ (Sσ unchanged)

法向黏结强度为变量下的边界受力比值曲线以Tσ/Sσ=4为界,以先减后增的趋势发展,如图12所示。Tσ/Sσ<4时,随法向黏结强度增大,试样中接触力场在竖向增速较大。法向黏结强度对颗粒间发生法向拉裂提供了一定阻尼,增强了颗粒间的黏附力,从而阻止颗粒发生侧向挤出,宏观即表现为侧面墙体受力增速随法向黏结强度增大而减小。Tσ/Sσ>4时,侧板受力增速开始提升,且比底板受力增速大。法向黏结强度过大时,颗粒接触键在法向上的黏附性进一步得到加强,但在切向力学性质保持不变的情况下,试样力学性质转为受切向指标控制,其整体性并不能进一步加强或得到维持。

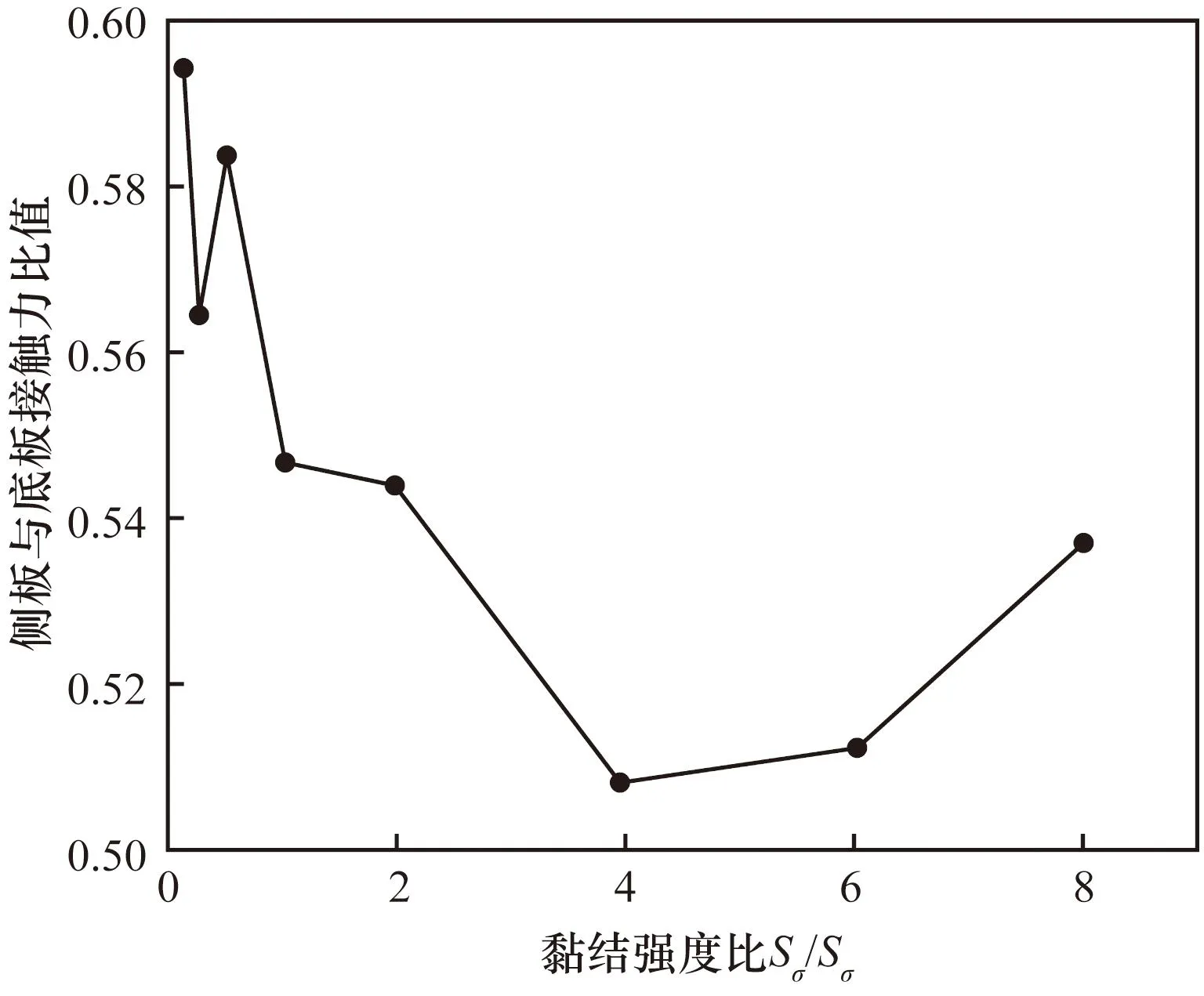
图12 试样筒侧板与底板所受法向力比值随Tσ/Sσ(Sσ不变)的变化Fig.12 Change of normal force ratio between side plate and bottom plate of sample cylinder with Tσ/Sσ (Sσ unchanged)

维持法向黏结强度不变,切向黏结强度作为自变量的不同Tσ/Sσ对应墙体受力曲线如图13所示。

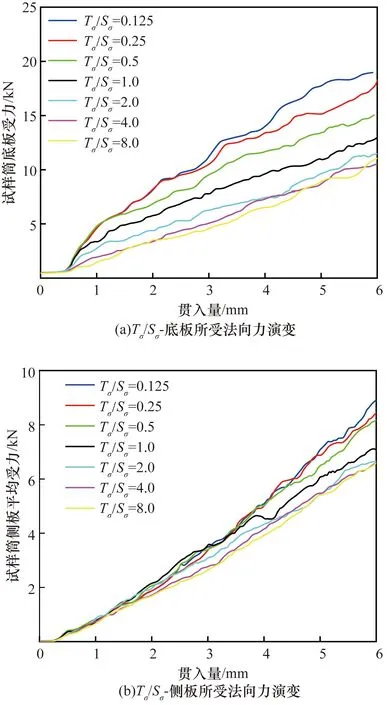
图13 不同Tσ/Sσ(Tσ 不变)对应试样边界受力的演变Fig.13 Evolution of stress on the boundary of samples corresponding to different Tσ/Sσ (Tσ unchanged)

可以看出,各曲线离散性较好,侧板受力曲线的斜率随切向黏结强度增大相应增长,底板受力曲线斜率则较为一致,表明切向黏结强度对接触力场形状的形成与发展具有重要作用。

图14为切向黏结强度对墙体接触力比值的变化,可见其同样以Tσ/Sσ=4为界,将曲线分为变化率方向不同的两段,从变化幅度来看,切向黏结强度对接触力场长细比的影响明显要比法向黏结强度大。Tσ/Sσ<4时,随切向黏结强度减小,侧板受力的增速明显大于底板受力。切向黏结强度较大时,接触键切向可传递一定的力和力矩,使相邻颗粒发生同方向运动的概率提高,可视为现实岩土体中的咬合力。咬合力过大时,颗粒切向相互锁止,阻碍颗粒的侧向位移,对发生剪胀现象不利,故此时侧板与底板接触力比值较小。随咬合力减小,颗粒侧向力链的发展愈加顺畅,整体力链网络以原先的竖向为主转变为接近圆形扩散,则侧板受力的扩张速率大于底板。Tσ/Sσ>4时,切向黏结强度较小,颗粒表面切向主要由动摩擦阻碍切向力做功,力链整体传导方向基本固定,且由于试样的剪胀效应已到达极限,侧板与底板的受力比曲线趋于平缓下降。

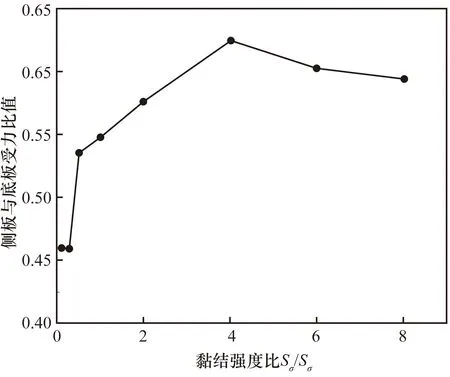
图14 试样筒侧板与底板所受法向力比值随Tσ/Sσ(Tσ不变)的变化Fig.14 Change of the ratio of normal force on the side plate and bottom plate of the sample cylinder with Tσ/Sσ (Tσ unchanged)

3 结论

借助PFC3D对CBR试验进行模拟,研究了级配碎石颗粒在CBR试验全过程中的运动轨迹及受力情况,结合力链模型对试样中颗粒接触力的传递进行分析,确定线性接触键模型中各参数对接触力场的作用机理,得出如下结论。

(1)由侧板及底板所受法向力演化,分析其比值变化得出:随贯入量增加,侧板受力过程经历了急速增加与衰退及继续较快增加3个阶段,依次反映试样颗粒向两侧排挤、水平向力链在试样上部扩展,颗粒接触键开始切向破坏、试样竖向被力链贯穿,试样在法向力作用下侧向约束增长速度较大。并且在整个过程试样整体仍以竖向挤压为主。

(2) 通过分析不同刚度比kn/ks、摩擦系数μ与黏结强度Tσ(设定Tσ/Sσ=1)对试样接触力场形状的作用机理,发现:以kn/ks=6为界,随法向刚度的增大,接触力场长细比先增加后减小;摩擦系数及黏结强度的影响逻辑较为清晰,都是通过改变接触键切向抵抗强度及接触键破坏所需外力做功。随摩擦系数或黏结强度增大,接触力场长细比相应减小。μ可显著改变接触力场形状,其与接触力场长细比呈线性正相关。

(3) 在颗粒相对运动中黏结强度比中法向及切向参数所起的作用不同,分开研究。切向参数不变时,发现法向黏结强度对试样接触力场形状的影响较小;法向参数不变时,发现切向黏结强度对接触力场形状的形成与发展具有重要作用。进一步根据接触力比值与黏结强度比的变化,以Tσ/Sσ=4为界,随法向黏结强度增大,其接触力场长细比先增加后减小;随切向黏结强度增大,所得接触力场长细比变化趋势则为先减小后增加。