基于空洞空间卷积网络的点衍射干涉图像相位解包技术
王同盟, 高 芬*, 李 兵
(1. 西安工业大学 光电工程学院, 陕西 西安 710032;2. 西安交通大学 机械制造系统工程国家重点实验室, 陕西 西安 710049)
1 引 言
随着光刻技术由深紫外向极紫外领域发展,人们对光刻物镜提出了更高的检测精度要求,其所用球面、非球面的检测精度要求达到0.1~1 nm均方根(Root Mean Square,RMS)的水平[1-2]。点衍射干涉测量法利用微米尺寸针孔衍射产生的超高精度球面波前作为参考面,构成干涉测量系统,由于其不受传统干涉测量中标准参考镜本身面形精度的限制,理论上可以达到亚纳米级检测精度,为光刻领域的超精面形检测开辟了新途径。
点衍射干涉测量中主流的相位提取方法是相移法[3],即通过使用压电陶瓷相移器件(Piezoelectric Transducer, PZT)带动被测件多次移动,采集多幅干涉图,进而通过多步相移算法[4]实现相位提取。因在计算机进行相位提取处理时,反正切运算是必要的步骤,经该步骤相位将被限制在[-π,π]的范围内,这种导致相位不连续的现象被称为相位包裹,后续还需要对包裹相位进行解包裹处理才能复原出待测面形。为了解决这一问题,国内外学者已提出了许多相位解包方法,主要有两类:路径跟踪类算法和路径无关类算法。路径跟踪类算法是由局部向全局逐步展开,将被包裹的相位通过路径积分沿合适的路径还原,典型算法是Goldstein 分枝切割法(Branch Cut Algorithm, BCM)[5]和质量导向算法[6],这类算法的解包性能与路径密切相关,需要大量的计算和存储空间,并且迭代次数较多,计算速度较慢。此外,算法的收敛性以及对于图像噪声的鲁棒性也需要进一步提高。路径无关类算法是运用各类算法对图像进行最小二乘求解,最常见方法有快速傅里叶变换法(Fast Fourier Transform,FFT)、离散余弦变换法(Discrete Cosine Transform,DCT)[7]法等,这类算法可以处理一帧的干涉条纹图像直接得到解包结果,但误差较大,很难得到精确的相位信息。
同时,点衍射干涉图像具有以下特点:虽然采集到的干涉条纹信息都比较稳定,但与其他干涉条纹不同的是点衍射本身性质使得干涉条纹图像光强分布[8]符合一阶贝塞尔函数分布的规律,即越靠近中心光斑光强越强,距离越远光强越弱,得到的图像光强分布不均匀,利用上述几种常用解包方法可能并不能够达到理想的解包精度,并且受实验环境限制,干涉图像对空气扰动、温湿度变化等环境干扰极为敏感,不可避免会带有环境噪声,同时,还可能因为人为操作不当造成激光光束入射小孔没有对准,引入非对准误差。因此如何在尽量减小各种误差干扰的情况下完成高精度的相位解包是亟待解决的一个问题。虽然目前已存在的相位解包算法已经可以比较好得处理传统干涉测量的包裹相位,但对于点衍射干涉图像的解包精度仍需提高,因此,研究适用于点衍射干涉图像的高精度解包算法是必然需求。
近年来,深度学习技术在图像领域发展迅速,在图像分割处理[9]、去噪[10]、生物医学[11]、光学检测[12]等研究中均取得了良好效果,尤其是深度学习中的神经网络技术通过提取图像不同层次的特征,对图像像元进行分类预测,结果比许多图像处理传统算法更加优秀。在干涉图像处理领域,Spoorthi G. E 等[13]设计了一种名为PhaseNet 的神经网络用于相位解包,并使用通用的仿真数据进行训练,结果表明其可以在高噪声情况下取得良好结果;Zhang JunChao 等[14]将Seg-Net 用到干涉条纹图像的解包裹里,测试结果的平均像素分类准确率和平均均方根误差(Root Mean Square Error, RMSE)分别达到了90.04% 和0.003 4 rad;KaiQiang Wang[15]使用U-Net 对高混叠欠采样的火焰和细胞包裹相位进行解包,与传统方法相比优势明显;Teng Zhang等[16]使用DeeplabV3+网络对泰曼-格林干涉仪和散斑干涉仪采集的条纹图像进行处理,证明了深度学习方法在解包精度和抗干扰性上表现优异;在对点衍射干涉图像的处理上,Zhuo Zhao等[17]先使用残差自编码器对包裹相位进行解包仿真了其正确性,后又设计了一种超列卷积[18]的方法对单帧条纹图像直接进行解包,并进行了仿真和干涉实验验证,但其精度仍有不足。
基于上述研究背景,本文将深度学习技术引入小孔点衍射干涉测量中,设计了一种结合空洞卷积金字塔[19]的自编码器结构,将相位解包任务看作类语义分割的像素级分类任务,利用网络模型预测被包裹相位的条纹阶次,最后将被包裹相位与其所在的条纹阶次的2π 倍相加,完成相位解包,此外对于被误分类的像素点,基于二分类训练的方法对其行误差校正进一步提高分类精度。仿真和实际干涉图处理结果均表明所提出的方法可以获得高精度的解包相位且具有很高的时间效率。
2 原 理
2.1 解包原理
在时域相移算法中,包裹相位的提取一般通过用N步相移算法计算得到,该算法在固定的相移量下进行N步相移,采集多幅干涉图像,设Ii(x,y)表示采集的第i帧图像;第i步相移引入的相移量为δi=(i-1)π/2,i=1,2,…,N;I0(x,y)表示干涉图背景强度;γ(x,y)表示条纹对比度;φ(x,y)是待提取相位,则有:
待提取的相位通过公式(2)求得,由于在求解后相位会存在2π 的跳变,对被包裹的相位进行展开才能得到被测物的绝对相位。
根据相位解包算法,绝对相位ϕ(x,y)和包裹相位φ(x,y)之间的关系可描述为公式(3):
其中,k(x,y)表示像素点所在的条纹阶次,确定阶次后只需加上相应相位阶次的2π 倍即可。
2.2 空洞空间卷积神经网络的构建
神经网络的任务是确定每一个包裹相位的像素点所在的阶次,因此本文将相位解包看作为一个像素级分类任务,每个包裹相位所在的阶次k(x,y)作为输出。提出了一种结合空洞空间卷积池化金字塔(Atrous Spatial Pyramid Pooling,ASPP)的卷积神经网络(Convolutional Neural Networks, CNN)来完成任务,其结构如图1所示。

图1 ASPP-CNN 神经网络结构Fig.1 Neural network structure of ASPP-CNN
相位解包任务中,最需要注意的是每个周期的包裹相位边界关系特征,因此在所提出的方法中CNN 采用了编码-解码器结构,多尺度特征融合等方法提高分类准确率。使用的输入包裹相位图像为128×128 pixel,通道数为1,网络主要有卷积层、池化层、上采样层组成,在编码-解码器结构中卷积核的大小为3×3 用来提取图像的特征,并对图像进行边界扩充以保证卷积后输出与输入大小一致,卷积后进行批标准化(Batch Normalization,BN)操作,对参数进行归一化,保证网络训练的稳定性,激活函数选择Relu 函数。以两层卷积层为一组加入一个残差结构以解决多次训练导致的网络退化问题,残差结构的输出与两次卷积的输出进行叠加。最大池化层会对图像进行下采样,以便对图像更深度的特征进行提取。解码器部分则会通过上采样逐步恢复图像尺寸,由于相位阶次的分类对每个像素的分类精度都有要求,因此残差块与卷积层的叠加结果会经过一次1×1 卷积调整通道数后作为最后像素分类的低尺度特征依据进行保留。最终叠加的特征图像会输入到空洞空间卷积池化金字塔结构中进行全局特征提取并通过Softmax 层输出预测像素值。对输入图像用不同扩张系数的空洞卷积进行运算得到不同感受野尺度的特征图,然后将每张特征图并联叠加用1×1 大小卷积核调整通道数使不同尺度的特征关系联系起来,实现可控的多尺度特征提取。
空洞空间卷积池化金字塔,如图2 所示,是对传统池化操作的改进。它首先是基于空洞卷积的,空洞卷积虽然被叫做卷积但它不只有卷积的功能,空洞卷积核在计算时会对参数之间进行填充空值,相当于卷积核变大但不会增加参数数量,卷积核尺寸变大会使卷积操作具有更大的感受野,使输出的特征图像更好地保留不同尺度的全局特征。
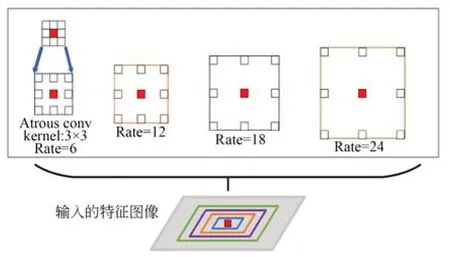
图2 空洞空间卷积金字塔结构Fig.2 Structure of ASPP
2.3 训练和验证
为了使神经网络达到最优效果,需要建立合适的数据集对其进行训练,数据集样本的丰富程度对训练效果的优劣起决定性作用。为提高深度学习算法对干涉条纹图像处理的能力,本研究的数据集由两部分组成:一部分是仿真图像,另一部分则由实验平台采集而来,仿真面形函数如表1 所示。

表1 仿真数据集的函数Tab.1 Unctions and parameters of simulated datasets
本研究使用表1 中的四个数学函数生成相位数据,并通过公式(1)中条纹图的强度分布方程以及小孔入射面上的高斯场分布初始化背景光强得到相应的干涉图集。为了提高训练效果,本文还引入高斯噪声和椒盐噪声产生了不同质量的图像,借助这些丰富多样化的数据集,可以对网络模型进行高精度训练。
得到多步相移干涉条纹图像后,通过相移法计算得到包裹相位图像,这里为了确保分类精度,使用7 步相移方法,相移算法如公式(4)所示:
神经网络的训练及测试过程如图3 所示。
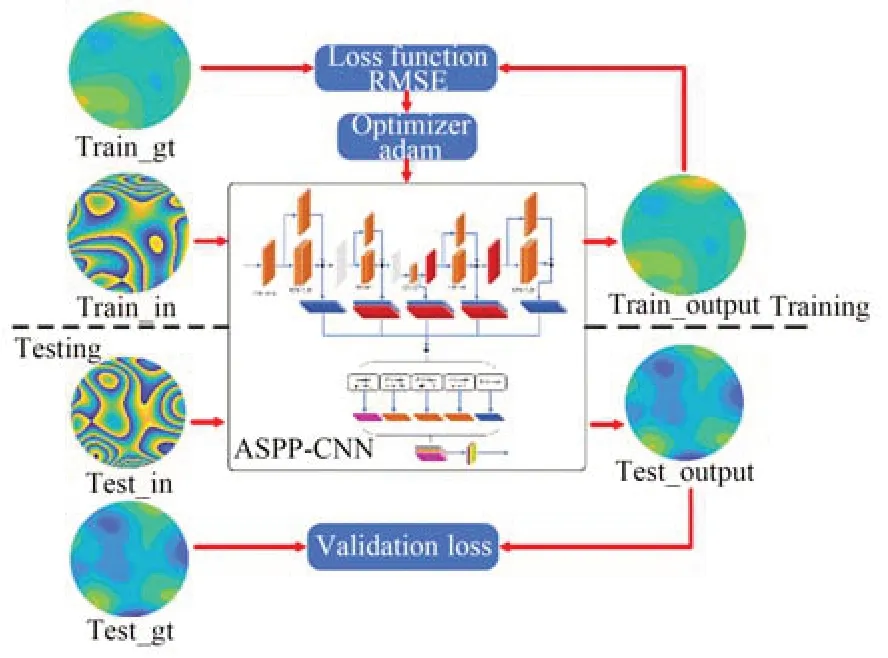
图3 神经网络的训练及测试过程Fig.3 Training and testing process of neural networks
训练前共生成和采集分辨率128×128 pixel的数据25 000 对,分成train 数据(23 000 对数据)和test 数据(2 000 对数据)两部分,其中train_in和test_in 中存放包裹相位,train_gt 和test_gt 中存放条纹阶次图。训练时将train_in 数据集中的数据作为输入,神经网络得到的预测相位阶次像素值与对应的train_gt 中的真实相位阶次值进行比较,损失函数使用均方根误差RMSE,根据公式(5)计算出预测值与真值之间的损失:
其中:Loss 表示每一个神经网络输出与真值的RMSE,m表示像素的个数;kt(x,y)表示真值;kp(x,y)表示神经网络的输出。
网络会根据损失使用自适应矩估计(Adam)优化器对模型参数进行更新,为了加快训练速度的同时保证训练的稳定性,采取动态学习率衰减机制,会根据训练状态调整学习率,具体调整策略为每5 个Epoch 学习率变为原来的0.85 倍,初始学习率设置为0.01,迭代训练轮数Epoch 设置为120,每一轮Epoch 训练结束后都会使用test 数据集对模型进行测试,同时记录训练损失与测试损失,保留损失值最小的模型参数。
图4 为训练过程的损失函数曲线,横轴表示迭代的次数,纵轴表示损失值,可以看出神经网络在迭代训练大约100 轮后收敛,最小损失RMSE 低于0.01。
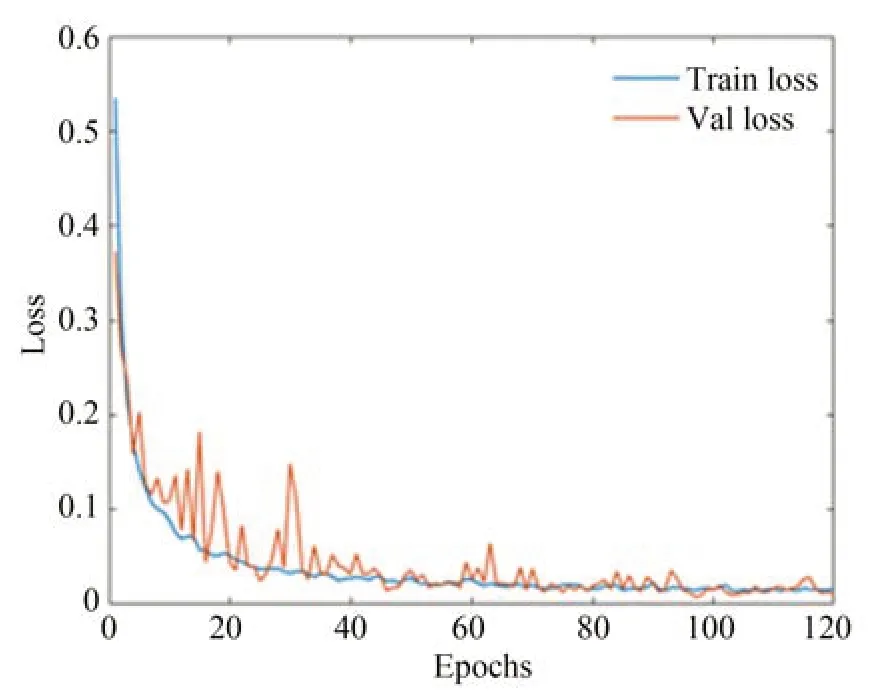
图4 损失函数曲线Fig.4 Loss function curve
训练完成后,使用模拟数据对模型性能进行测试,图5 和图6 分别使用球面仿真数据和随机曲面仿真数据来验证其性能。结果表明,本文所提出的解包方法在整体上有较高的精度,但在某些边缘仍然误差较大,球面解包结果残差的平均值为0.07 rad,最大残差值为0.94,随机曲面解包结果残差的平均值为0.09 rad,最大残差差值为1.07。
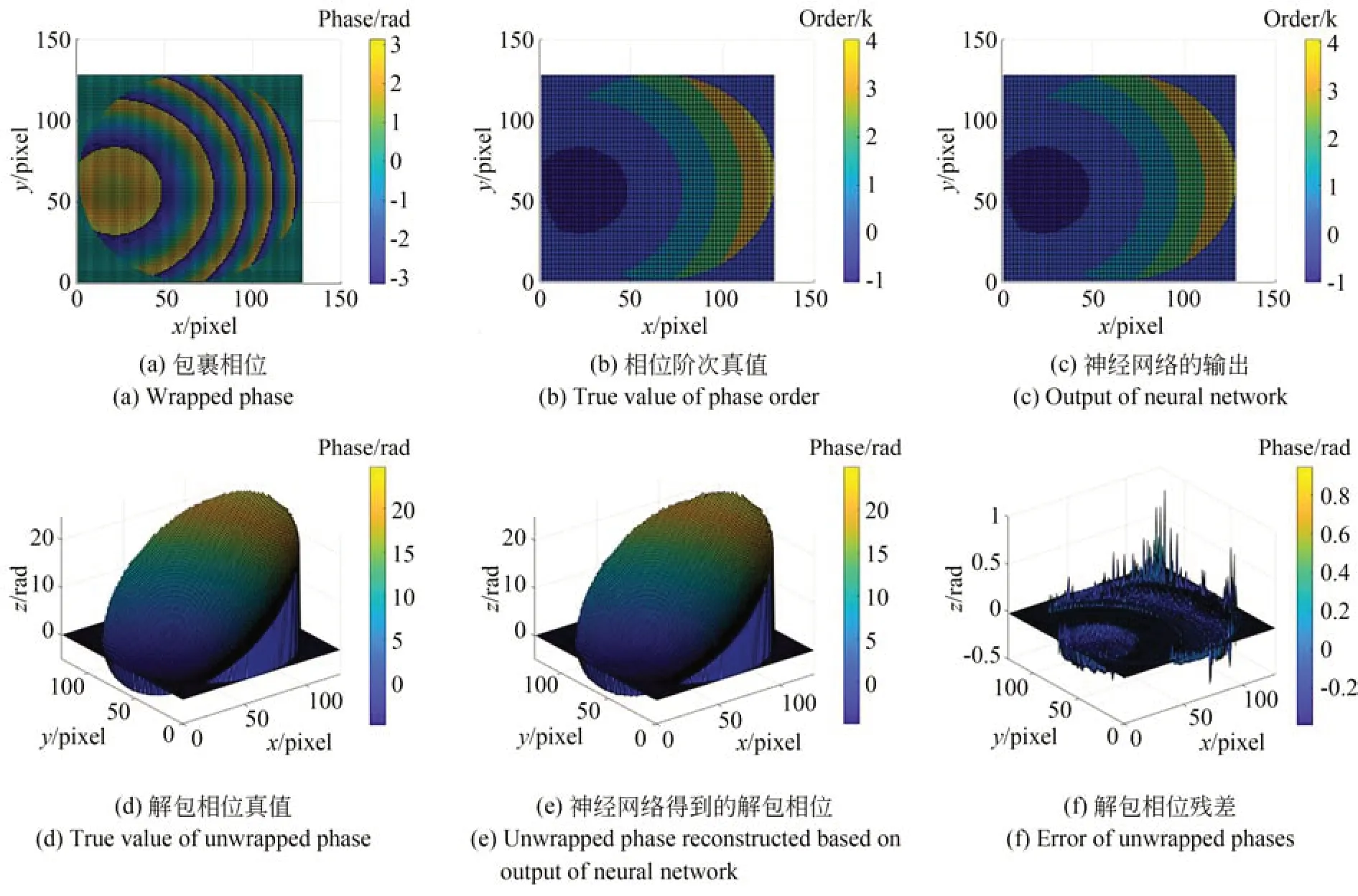
图5 球面数据的解包结果Fig.5 Unwrapping results of sphere

图6 随机曲面数据的解包结果Fig.6 Unwrapping results of random surface data
这些误差较大的点会对最终的面形拟合结果造成影响,为此本文提出了一种优化残差、提高解包精度方法。首先,由于相位阶次k(x,y)是整数,而神经网络的输出可能不为整,所以将Output 的值先取整,但此操作可能会将某些像素点误分类到其他阶次,造成更大的误差。第二步,将那些误分类的像素点正确归类看作二分类问题,所提出的神经网络模型仍然可以完成此项任务,只需将那些被误分类的图像重新设为训练输入Input,并设置相应的真值,重新训练即可,此时神经网络模型的任务变为最后对图像中的连通区域进行标记。最后根据标记结果对有误分类点的连通区域进行修正,修正后的球面和随机曲面解包图像和残差如图7 所示。可以看到,经过优化后,球面仿真数据的误差为0,随机曲面仿真数据的误差可减少至10-6rad,可以忽略不计。

图7 优化后的球面和随机曲面解包结果及残差Fig.7 Optimized unwrapping results and errors of spherical and random surfaces
在点衍射干涉测量系统的实际应用中,环境干扰使得干涉图像出现噪声是难以避免的,为了验证所提出方法对环境噪声的鲁棒性,分别在球面和随机曲面仿真数据上分别引入百分比为0.35 和0.25 的椒盐噪声来模拟环境噪声,从图8中可以看出该方法对有噪声干扰的包裹相位处理仍然非常精确,RMSE 值分别为0.024 8 rad 和>0.029 6 rad。
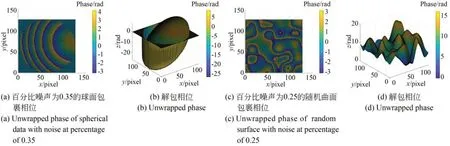
图8 引入环境噪声后的包裹相位数据及解包结果Fig.8 Wrapped phase data with simulated environmental noise and unwrapping result
3 实验与讨论
为了进一步验证所提出方法的有效性,本文基于点衍射相移干涉实验平台,采集实际点衍射相移干涉图像进行处理,并将所提出方法的结果与专业的干涉图像处理软件及其他方法结果进行对比,验证所提方法相位解包精度、面形拟合精度及时间效率。
3.1 实验平台
搭建的点衍射干涉测量系统如图9 所示,系统通过2.5 μm 小孔衍射产生球面参考波前,被测件为口径D=50 mm,曲率半径R=500 mm 的球面反射镜。
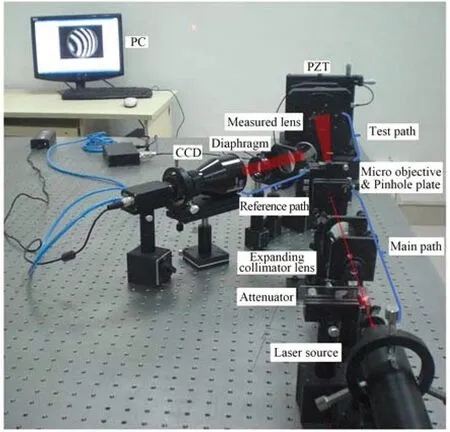
图9 点衍射干涉测量实验系统Fig.9 Point diffraction interferometry system
系统由氦氖激光器发出的激光光束经过衰减片后被扩束器准直入射到显微镜物镜。显微物镜将光束聚焦至小孔衍射板上的小孔后产生衍射光。衍射光沿中心光轴被分为两部分:一部分作为参考光路,另一部分作为测试光路。在测试光路中,PZT 被固定在一个五维调整架上,被测件被固定在PZT 上,部分衍射光到达被测件后经被测件反射回小孔基板,经镀有铬膜的小孔基板表面再次反射后进入参考光路,进入参考光路的测试光与参考光发生干涉后经准直镜和成像镜头被电耦合元件(Charge Coupled Device ,CCD)接收,在CCD 上产生干涉图像。CCD 和PZT 都直接连接到上位机上,PZT 可以由上位机控制,带动被测件进行移动,获得不同相移量的干涉图像。
为了获得高精度的相位提取结果,这里采用7 步相移算法,所采集到的相对相移量为π/2 的7帧相移干涉图像如图10 所示。可以看出,干涉条纹图像有一些噪点并且符合点衍射光强分布规律,后续使用ESDI 公司商业化干涉图像处理软件(Intelliwave6.5)进行处理,将处理结果与所提出方法及其他经典深度学习方法解包及面形拟合结果进行比较。
3.2 处理结果精度对比
将采集到的干涉图预处理提取圆域后运用公式(4)进行相位提取,得到包裹相位图像如图11(a)所示,图11(b)为使用本文所提深度学习方法对包裹相位图像进行解包的解包相位,图11(c)为解包相位经36 项泽尼克拟合后复原的待测面形2D 图。图12 给出了利用ESDI 专业干涉图像处理软件处理后得到的2D 面形结果,软件处理中选用内置的7A 相移算法进行相位提取、枝切法(BCM)进行解包、36 项泽尼克多项式进行拟合,将软件所给出的数值作为真值比较。

图11 包裹相位和基于ASPP-CNN 方法解包得到的解包及其2D 面形拟合结果Fig.11 Wrapped phase and unwrapped phase by ASPP-CNN method and 2D surface shape

图12 ESDI 干涉图像处理软件获得的面形与PV,RMS 值Fig.12 Surface shape, PV and RMS values obtained by ESDI interferogram analysis software
为了更直观地展示出本文方法的优越性,图13 给出了几种不同解包方法对图10 的解包处理结果及面形拟合结果,图13(a)列为本文所提方法、FFT 法以及U-Net 和DeepLabv3+神经网络、枝切法解包5 种解包方法结果对比,图13(b)列为5 种不同方法的解包结果经36 项泽尼克多项式拟合所得的面形对比,图13(c)列为面形差值。其中选用了与专业软件一致的枝切法,将其处理结果作为真值。
比较图11 和图12 可以看出:本文所提深度学习法解包复原得到的面形与专业图像处理软件处理结果接近,面形吻合度高,二者峰谷(Peak-to-Veally,PV)和RMS 测量结果均非常接近。由图13 可以看出,FFT 方法虽然可以在仅有一帧干涉条纹图像的情况下处理图像,但精度并不高,差距非常大,与专业干涉图像处理结果比较,其PV 差值达到了0.528λ;而U-Net 得到的解包结果虽然整体上完成了解包,但在中间小部分区域以及边缘区域误差较大,最终的面形拟合结果也显示其与真值的PV 差值有0.029λ,RMS差值为0.006 3λ,DeepLabv3+处理的结果则精度略高,PV 差值为0.020 2λ,RMS 差值为0.004 8λ,但Deeplabv3+的网络结构过于复杂,训练成本与时间效率与本文提出方法相比都更高,且最终处理结果精度也差于本文方法。
表2 列出了这五种方法的PV,RMS,RMSE值及处理时间,所提出方法处理速度最快,且与专业软件所得结果的PV 差值仅为0.012 1λ,RMS差值仅为0.004 2λ,由此验证本文所提方法具有较高精度,且在时间效率上有显著优势。
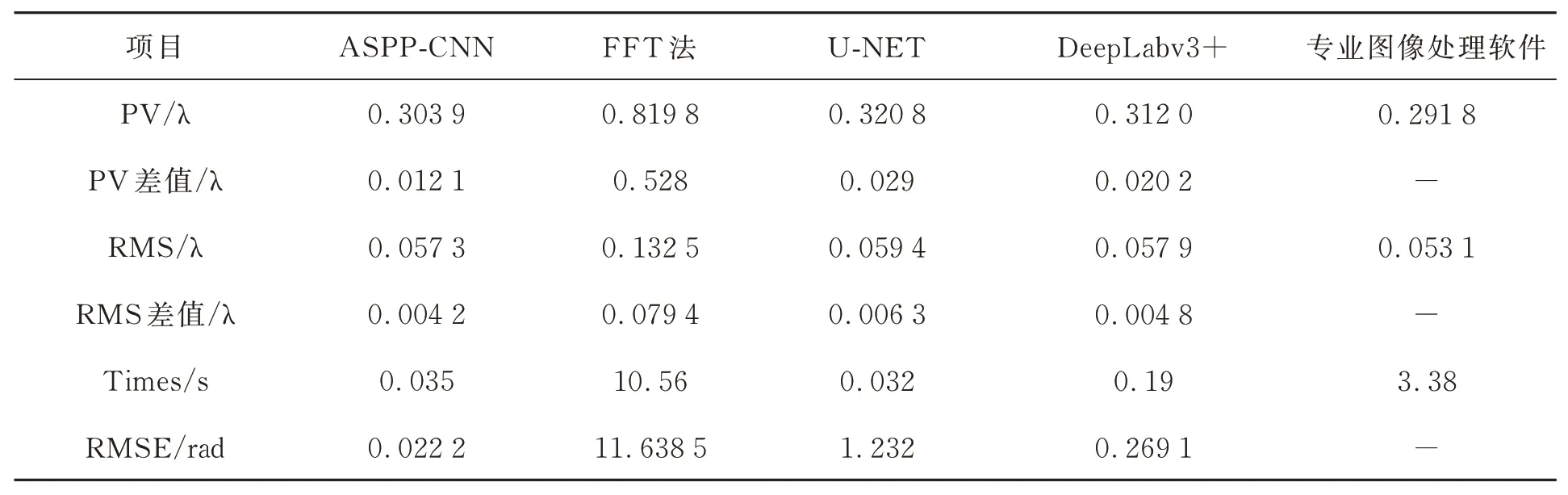
表2 不同方法的PV,RMS 值及处理时间Tab.2 PV, RMS values, and processing time of different methods
根据面形残差图像可以发现较大的差值出现在边缘位置,原因是在对图像进行预处理时,所采用方法为霍夫变换圆域提取算法[20]自动选取圆域,而专业图像处理软件的圆域需要手动提取,只能尽可能和所提取的圆域一致,并不能保证完全相同。
4 结 论
本文提出了一种基于神经网络的高精度点衍射干涉图像相位解包方法,首先构建了适用于点衍射干涉图像的CNN 网络,该网络集成了编码-解码器结构、ASPP 结构等以完成高精度的相位解包。此外,还构建了多样化面形数据集来提高网络训练效果,并设计了针对误分类点的优化方法,显著提升神经网络处理精度。仿真结果表明,本文所提出的方法能够实现与真值差异基本为0 的解包结果。将该方法应用于点衍射干涉测量系统并进行实验验证,结果表明,所得到的结果与专业干涉图像处理软件具有较高一致性(RMSE=0.022 2 rad,PV 差值为0.012 1λ,RMS差值为0.004 2λ),同时时间效率也远快于传统方法。仿真和实验均证明该方法具有适用性强、高精度、时间效率高的特性,并可为一类相移压包图像的高精度解包提供有效手段,具有普适性。
在使用本文所提出的方法时需要注意其存在以下问题:由于神经网络结构限制,无法对不同分辨率图像进行一致处理。因此,今后的工作将重点研究单帧条纹图像的相位恢复问题以及动态分辨率图像的一次性相位恢复技术。

