旋变二次谐波测角误差自校正

王英广， 张激扬， 张 强， 鲁 明， 田利梅

（北京控制工程研究所，北京 100094）

1 引 言

控制力矩陀螺（ Control Moment Gyroscope，CMG）作为大型航天器进行快速姿态调整的常用惯性执行机构，由高速转子和低速框架组成［1-2］。伺服电机驱动低速框架改变高速转子角动量的方向输出力矩。框架转速精度和稳定度直接影响控制力矩陀螺输出力矩精度和稳定度［3-4］。

因为旋转变压器（简称“旋变”）具有良好的空间环境适应性，控制力矩陀螺使用旋变检测框架角位置。旋变测角精度直接影响控制力矩陀螺的力矩控制精度和反馈给姿控分系统的角动量指向精度，进而影响姿控系统控制精度［5-6］。

高精度旋变一般使用跟踪式旋变-数字信号转换器（Resolver-to-Digital Converter，RDC）解算角位置信息［7］。旋变解调是在假定旋变输出正余弦信号包络是等幅、正交的基础上进行的。但受加工、装配误差和磁场不均匀等因素影响，旋变输出正余弦信号包络存在幅值不一致、非理想正交的情况。同时，RDC 对旋变输出正余弦信号进行处理时，存在非等幅放大及相位偏移的问题。以上原因均会导致RDC 解调角速度中产生二次谐波误差，这是旋变测角误差的主要来源［8］。为提高旋变测角精度，需要对旋变二次谐波误差进行校正补偿。

ALEMI R M 等优化旋变结构及电磁设计，降低磁场谐波失真，提高测角精度，但其谐波误差降低幅度有限［9］。

肖越华使用精密转台标定旋变，得出误差曲线，对其进行频谱分析，获取主要频率成分的参数并进行补偿［10］。孙伟使用高精度分度头标定旋变，得到误差曲线，设计查找表，对低精度旋变进行补偿［11］。李婧等使用经纬仪标定旋变误差，并进行软硬件补偿［12］。如上方法均使用高精度角度传感器标定旋变，且标定在旋变安装到伺服系统之前进行，安装到伺服系统后的误差特性会随旋变定转子的相对位置等因素变化。

Wu Z 使用二阶梯度估计器对旋变输出正余弦信号进行等幅、正交校正，以降低旋变测角误差，使用软件实现RDC 解调功能［13］。BUNTE A使用增益调节器、相位调节器校正旋变输出信号，同时对偏置误差进行校正［14］。如上方法均对旋变输出信号进行校正，获得等幅、正交的正余弦信号。而未考虑RDC 解调过程中的非等幅放大及相位偏移情况。

Qin H［15］，Guo M［16］，WANG R［17］，JANG P［18］使用高精度AD 转换器直接采集旋变励磁正余弦信号并进行高速、复杂的运算获取完成RDC 解调，获取高精度的角位置。而这对AD 转换器精度及处理器运算速度要求极高，难以应用于航天器中。

针对旋变测角误差的主要成分——二次谐波误差，本文提出了一种基于特征频率参考的二次谐波误差自补偿方法。首先，对旋变测角误差机理进行分析，得出旋变正余弦输出信号的非等幅、非正交特性产生互不相关的二次谐波误差。而后分析可知对旋变输出信号进行幅值调整和相位差调整可产生互不相关的二次谐波误差校正量。然后，在旋变和RDC 之间加入由运算放大器构成的幅值校正器和相角校正器。最后，根据误差信号在控制系统中特征频率不变的特性，对框架伺服电机进行匀速控制，以角速度频谱中的二次谐波频率的幅值为参考基准，调整幅值校正器和相角校正器，产生二次谐波校正量，对旋变二次谐波误差进行自校正。

2 旋变测角原理

旋变测角系统由旋变本体和旋变解调器组成。跟踪型数字信号转换器RDC 因具有编码精度高、抗干扰能力强、稳定性好等优点，被广泛应用于旋变解调中。图1 为解调原理图，将频率为ω的信号sin(ωt)施加到旋变本体输入端，旋变输出与转子角位置θ相关的正余弦包络信号Acos(ωt)sinθ和Acos(ωt)cosθ。两信号分别与RDC 解调角位置φ的正余弦值求积得到Acos(ωt)sinθcosφ和Acos(ωt)cosθsinφ。然后求差得到Acos(ωt)sin(θ-φ)，相敏检测后得到Acos(ωt)sin(θ-φ)cos(ωt)，对其进行积分可得A′(θ-φ)，再进行跟踪速率调整，经过压控振荡器（Voltage Controlled Oscillator，VCO）和闭环跟踪控制后，可使θ-φ=0，实现解调角位置φ跟踪旋变角位置θ。

图1 跟踪式RDC 解调原理图Fig.1 Demodulation principle Diagram of Tracking RDC

3 旋变误差分析

跟踪式解调是在假定旋变输出正余弦信号包络是等幅、正交的基础上进行的。但受加工、装配误差和磁场畸变等因素影响，旋变输出正余弦信号存在幅值不一致、非理想正交的情况。同时，RDC 对旋变输出正余弦信号进行处理时亦存在非等幅放大及相位偏移的问题。这均会产生旋变幅值误差和正交误差等二次谐波误差。

3.1 旋变幅值误差

幅值误差是由旋变正余弦输出信号幅值不同和RDC 对正余弦信号放大系数不同引起的误差。

假定以旋变输出正弦信号的幅值A1为基准，旋变输出余弦信号幅值为A1(1+δ1)。以RDC 对正弦信号的放大倍数值A2为基准，RDC余弦输入信号放大倍数为A2(1+δ2)。旋变正弦信号综合放大倍数为A1×A2=A，余弦信号综合放大倍数为A1(1+δ1)×A2(1+δ2)=A(1+δ)。则有RDC 跟踪误差e为：

其中：δ为幅值误差，φ为RDC 解调角位置，θ为旋变实际角位置，K=Acos(ωt)×cos(ωt)，因δ远小于1，式（1）化简为：

RDC 闭环控制后，跟踪误差e趋于零，解调角位置φ变为：

因此，由幅值误差δ导致的RDC 角度解算误差为：

又因δ远小于1，式（4）简化为：

对应的角速度误差为：

由式（6）可见，由幅值误差导致的角速度误差也是周期性误差，误差频率为角速度的2 倍，误差大小为角速度与幅值误差的乘积。

3.2 旋变正交误差

正交误差是指由旋变正余弦输出信号不正交和RDC 采样相位差造成的旋变测量误差。

假定以旋变输出正弦信号为基准，旋变输出余弦信号的相位偏移为Δ1θ。以RDC 对正弦信号的采样相角基准，RDC 对余弦输入信号的相位偏移为Δ2θ。旋变余弦信号相位偏移为Δ1θ+Δ2θ=Δθ，也称为旋变正交误差，则由正交误差引起的RDC 跟踪误差为：

其中：∆θ为正交误差，φ为RDC 解调角位置，θ为旋变实际角位置，K=Acos(ωt)×cos(ωt)，因Δθ远小于1，则式（7）化简为：

RDC 闭环控制后，公式（8）趋于零，则解调角位置φ为：

因此，由旋变正交误差Δθ导致的RDC 角位置解算误差为：

对应角速度误差为：

由上式可见，正交误差引起的角速度误差也是周期性误差，误差频率为角速度的2 倍，误差大小为角速度与相角误差的乘积。

幅值误差、正交误差等反应在速度频谱上表现为旋变转频的二倍频，统称为二次谐波误差，其为旋变测角误差的主要成分，占比达到85%以上［10］。

4 二次谐波误差校正方法

旋变二次谐波角速度误差可用下式表示

其中：Acs为误差幅值，α为初始相角?为角速度。

由第3 节旋变误差分析可知，旋变幅值误差δ̇cos (2θ)和正交误差∆θ̇sin(2θ)是互不相关的二次谐波角速度误差。反过来讲，对旋变输出正余弦信号的幅值之比进行调节，假设调节量为Acos，则可产生二次谐波角速度误差的余弦校正量为：

对旋变输出正余弦信号的相位偏移进行调节，假设调节量为Asin，可产生二次谐波角速度误差的正弦校正量：

因余弦校正量和正弦校正量互不相关，可分别进行校正，即：

由式（15）解算，当Acos和Asin满足如下条件时：

可实现对二次谐波角速度误差的校正。

4.1 幅值误差校正

在旋变余弦输出信号与RDC 间加入幅值调节器，如图2 所示，调节系数设为Ac，则RDC 跟踪误差由公式（1）变为：

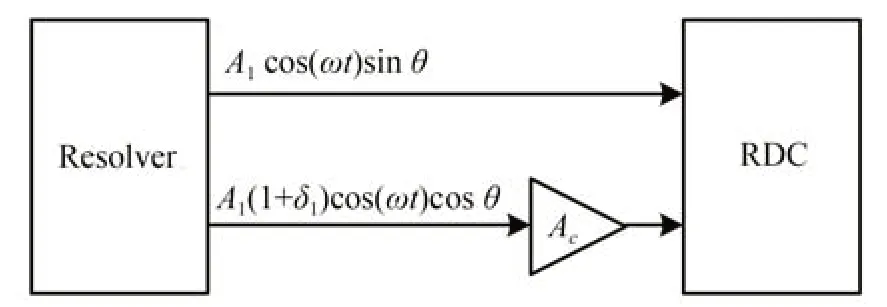
图2 旋变幅值误差校正原理图Fig.2 Principle block diagram of correcting amplitude error

可得，RDC 解调角位置φ=θ，解调角位置φ跟踪旋变角位置θ，由幅值误差δ引起的RDC 角度解算误差变为零。

4.2 正交误差校正

使用幅值调节器可以方便地调节旋变输出信号的幅值，实现幅值误差的校正。而在不影响幅值的前提下，难以通过单一输出信号的处理来调节旋变两个输出信号的相位差。

为此，提出一种交叉调节方法，如图3 所示，将旋变输出正弦信号乘以正交校正系数Aθ与旋变输出余弦信号相加后，引入到RDC 余弦输入端，正交误差引起的RDC 跟踪误差由公式（7）变为：

因∆θ远小于1，式（19）可化简为：

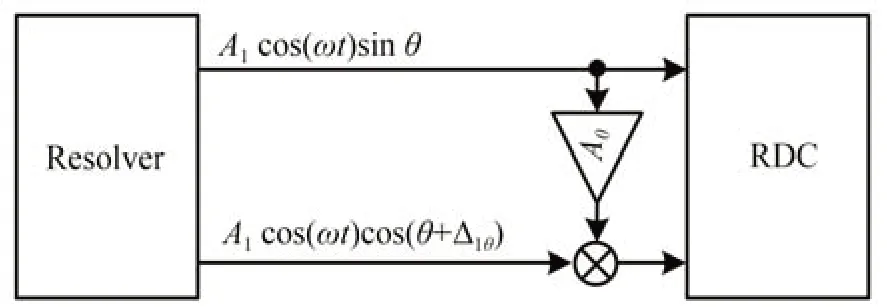
图3 旋变正交误差校正原理图Fig.3 Principle block diagram of correcting quadrature error

由旋变正交误差Δθ导致的RDC 角位置解算误差为：

当正交校正系数为Aθ等于旋变正交误差Δθ时，可实现正交误差校正。

4.3 误差校正参考

上文讲述了二次谐波误差的校正方法。而观测误差是校正误差的前提。在此提出一种测角谐波误差自校正方法，无需第三方高精度测角传感器标定。首先，控制框架电机匀速旋转，则旋变二次谐波误差频率固定，为转频的2 倍。根据定常线性系统的频率保持性，旋变二次谐波误差频率反应在转速频谱上也为转频的2 倍，且此频率的幅值可表征旋变二次谐波误差大小。

图4 所示为基于旋变测角的伺服控制系统，Rp为二次谐波测角误差，Rv为等效二次谐波角速度误差，νout为根据RDC 测角进行微分得到的角速度，C（s）为Rv到νout的传递函数，则νout中Rv引起的误差成分为：

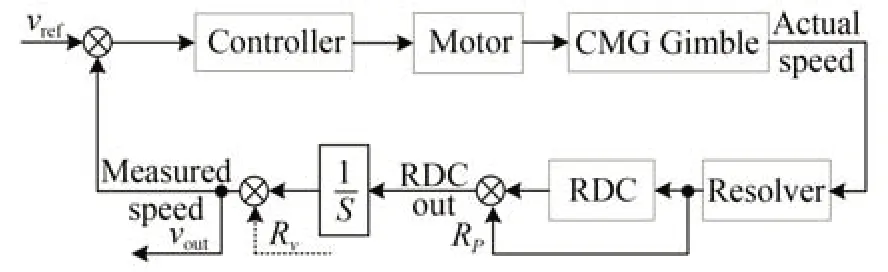
图4 基于旋变测角的伺服控制系统框图Fig.4 Block diagram of servo control system using resolver

设定伺服系统指令角速度为ω，带入公式（12），则有旋变二次谐波角速度误差为：

传递函数C（s）在2ω处的频率特性可表示为：

将公式（23）和公式（24）带入公式（22）得：

由公式（25）可见，根据定常线性系统的频率保持性，系统在简谐信号Rv的激励下，所产生的稳态输出νout_Rv也是简谐信号。对νout其进行FFT 变换，在频谱结果中νout_Rv表现为频率为ω/π幅值为A(2ω)Acs的特征频率。此特征频率可表征二次谐波测角误差Rp的大小。在公式（25）中只要获知特征频率值，然后以频谱结果中此特征频率的幅值为参考，分别调整幅值调节系数Ac和相角调节系数Aθ，降低直至消除旋变二次谐波误差的正弦分量和余弦分量，进而消除旋变二次谐波误差。

5 仿 真

按照图4 控制系统框图，根据第2 节旋变解调原理建立旋变及RDC 的仿真模型。旋变为粗精机双通道型，精机极对数为32。设定旋变精机幅值误差为0.02，正交误差也为0.02。伺服控制器使用速度-电流双闭环控制方法，依据RDC 输出微分得到的检测转速与指令转速之差运算得出控制量，控制伺服电机驱动CMG 框架跟踪指令转速23 （°）/s 稳速旋转。

未校正的CMG 框架转速仿真曲线图如图5所示，因为旋变精机幅值误差及正交误差的存在，CMG框架实际转速存在频率为4.09 Hz的波动，波动幅值为0.63 （°）/s。CMG 框架旋变测量转速也存在频率为4.09 Hz的波动，波动幅值为0.15 （°）/s。

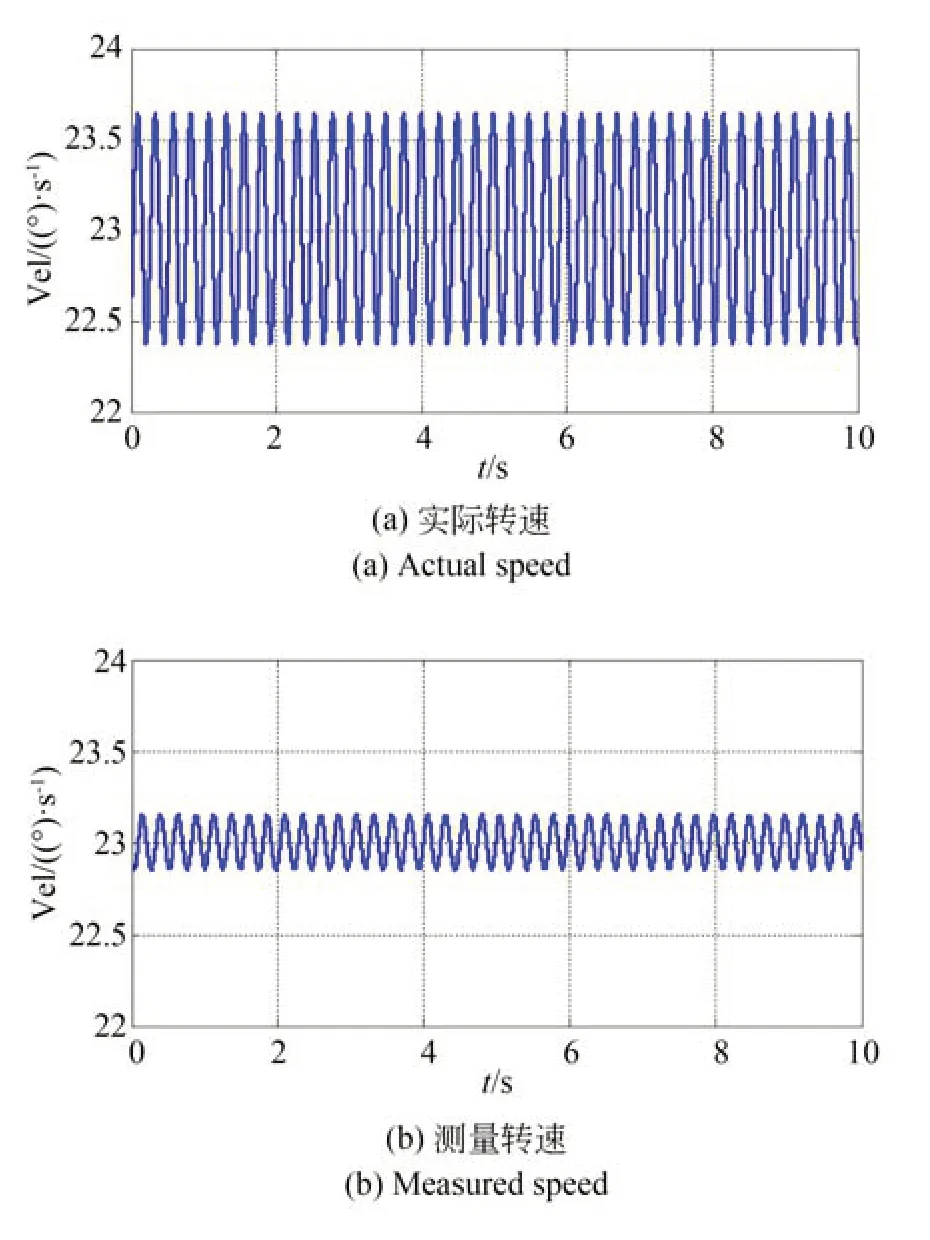
图5 未校正时CMG 框架转速仿真曲线Fig.5 Simulation of CMG gimble speed without calibration

因CMG 框架伺服系统以旋变测量转速作为速度反馈，旋变测量误差经伺服控制器后形成错误的控制量，进而导致CMG 框架的实际转速中产生与旋变测量误差频率一致的速率波动，而此速率波动与旋变自身测量误差部分抵消，造成框架实际转速速率波动大于旋变测速速率波动。

5.1 幅值误差校正仿真

在仿真模型中增加如3.1 节的幅值误差校正环节，将幅值误差校正系数Aθ设置为1/1.02，CMG 框架转速仿真结果如图6 所示，实际转速速率波动幅值为0.45 （°）/s，旋变测量转速速率波动幅值为0.11 （°）/s。速率波动量均比未校正时下降29%左右。

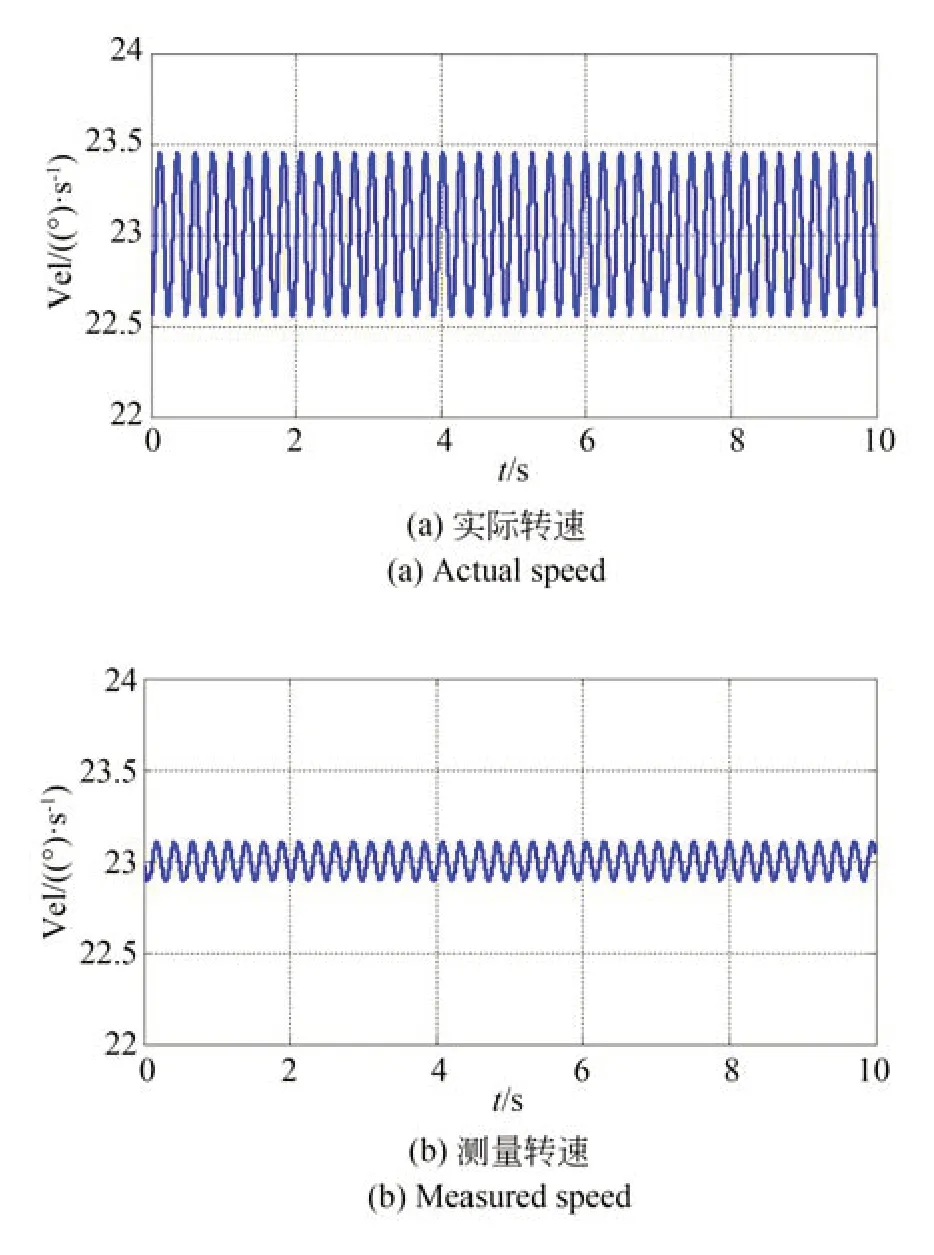
图6 幅值误差校正后CMG 框架转速仿真曲线Fig.6 Simulation of CMG gimble speed after correcting amplitude error

5.2 正交误差校正仿真

在仿真模型中增加如3.2 节的正交误差校正环节，将正交误差校正系数Aθ设置为0.02，CMG 框架转速仿真结果如图7 所示，实际转速波动幅值为0.004 3 （°）/s，旋变测量转速波动幅值为0.001 1 （°）/s。速率波动量均比未校正时下降99%以上。

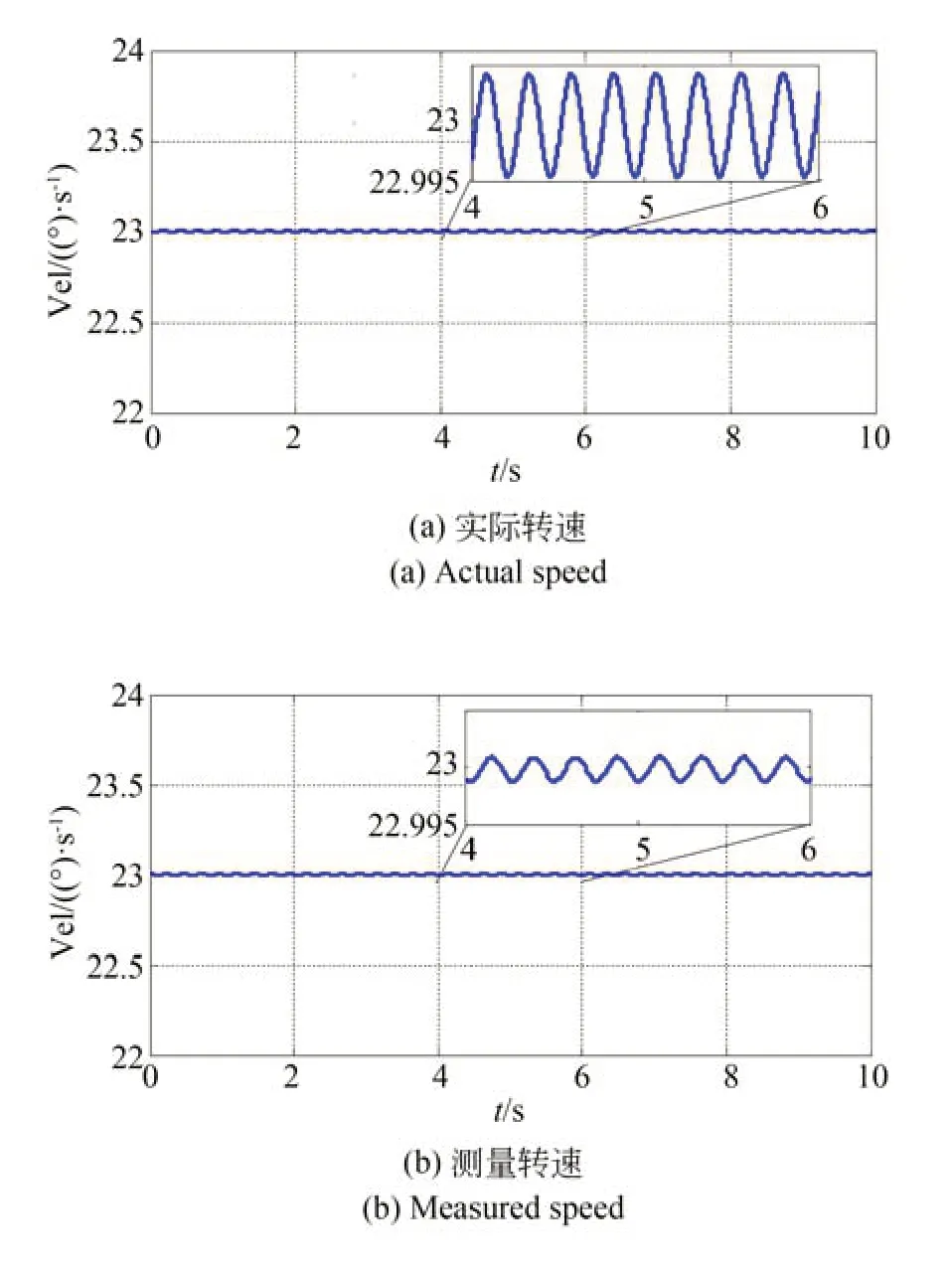
图7 正交误差校正后CMG 框架转速仿真曲线Fig.7 Simulation of CMG gimble speed after correcting quadrature error

6 实 验

在某CMG 产品上进行旋变二次谐波误差校正试验，其旋变选用粗精机双通道型，精机极对数为32。伺服控制器使用速度-电流双闭环方法，依据RDC 输出经过微分器得到的检测转速与指令转速之差运算得出控制量，控制伺服电机驱动CMG 框架跟踪指令转速23 （°）/s 稳速旋转。

低速框架的旋变测量角速度频谱结果如图8所示，最高峰值频率为4.09 Hz，即为旋变测角的二次谐波误差，其幅值为0.116 5 （°）/s。除二次谐波外，四次、八次谐波和电机磁槽谐波幅值也较明显。

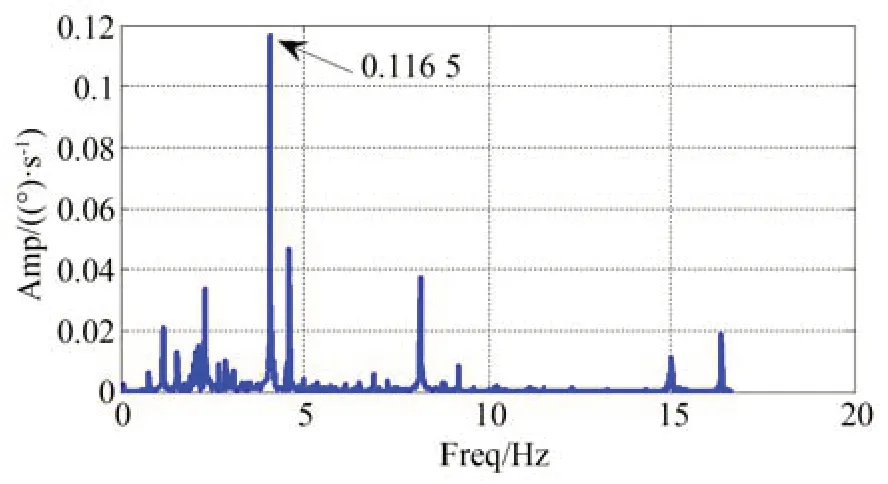
图8 未校正时CMG 框架旋变测量转速频谱图Fig.8 Spectrum curve of measured speed of CMG gimble without calibration

6.1 幅值校正

如图9 所示，使用比例放大器搭建幅值误差校正器，放置于旋变精机正弦输出和RDC 之间。伺服电机驱动CMG 框架以23 （°）/s 转速旋转。对旋变测量转速进行频谱分析。调整同向放大器放大系数，使频谱结果中4.09 Hz 频率的幅值下降到不能再小为止。此时的旋变测速曲线频谱如图10 所示，进行幅值校正后，旋变测得的二次谐波误差幅值降为0.102 （°）/s。

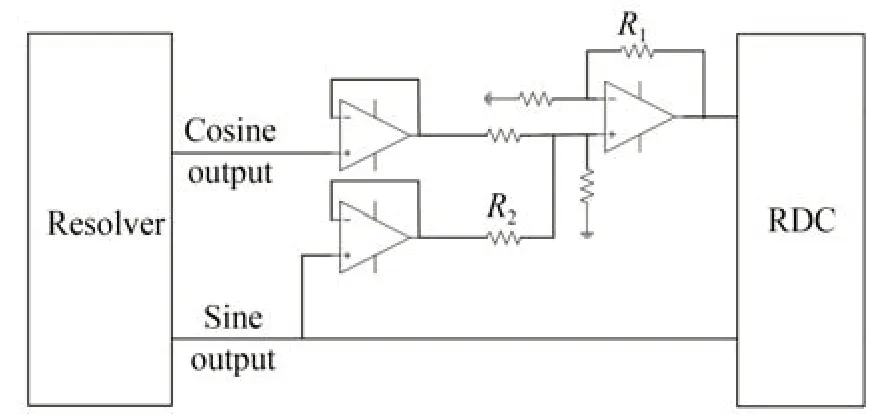
图9 旋变误差校正结构框图Fig.9 diagram of resolver error corrector

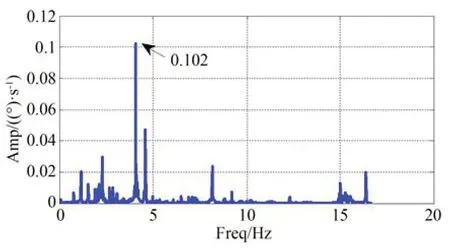
图10 幅值误差校正后CMG 框架旋变测量转速频谱图Fig.10 Spectrum curve of measured speed of CMG gimble after correcting amplitude error

6.2 正交校正

在幅值校正的基础上进行正交校正试验。如图10 所示，使用运算放大器搭建加法器，将精机余弦输出叠加到精机正弦输出上，构成交叉调节相角校正器。伺服电机驱动CMG 框架以23（°）/s 转速旋转。对旋变测量转速值进行频谱分析。调整加法器中精机余弦输出的电阻阻值，即调整正交校正系数，使频谱结果中4.09 Hz 频率的幅值下降到不能再小为止。

此时的旋变测速曲线频谱如图11 所示，进行正交校正后，旋变测得的二次谐波误差幅值降为0.0250 6（°）/s，比未进行任何校正时降低78.5%。同时旋变四次谐波幅值比校正前也有明显下降。存在残余二次谐波误差的原因是手动调节电位器阻值精度所限。

图11 正交误差校正后CMG 框架旋变测量转速频谱图Fig.11 Spectrum curve of CMG gimble’s measured speed after correcting quadrature error

二次谐波误差校正前后的旋变测速曲线如图12 所示，校正前的速率稳定度为0.335 （°）/s，校正后的速率稳定度为0.199 （°）/s，波动量降低40.5%。残余波动主要由伺服电机电磁扰动、外部扰动力矩、旋变测速噪声等引起。

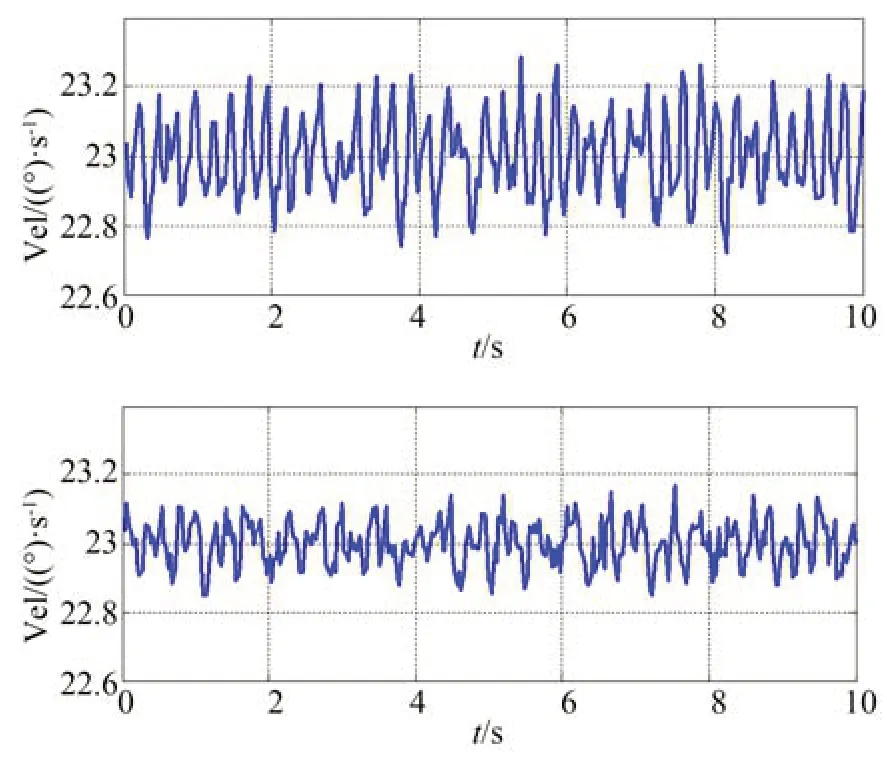
图12 二次谐波误差校正前后的旋变测速曲线对比Fig.12 Comparison of measured speed before and after correcting Second harmonic error

7 结 论

为补偿旋变正交误差和幅值误差，本文提出了基于特征频率参考的旋变二次谐波误差自校正方法。在旋变和RDC 之间加入幅值校正和正交校正环节。控制CMG 框架定转速旋转，对RDC 输出进行微分得到的转速进行频谱分析。参考频谱中二次谐波幅值调整幅值校正器和相角校正器，对旋变的测角误差进行自校正。本方法在CMG 产品上进行了试验，试验结果表明，旋变二次谐波测角误差幅值降低了78.5%，伺服系统速率波动量降低了40.5%。大幅提升了旋变测角精度和伺服系统的转速度稳定度。