面板数据中方差的共同变点估计

赵军辉，董翠玲

（新疆师范大学 数学科学学院，新疆 乌鲁木齐 830017）

面板数据结合了时间序列与截面数据的特点，是二维数据，它扩大了样本的信息，降低了变量之间的多重共线性，提高了参数估计的准确性，目前广泛应用于经济学、金融学、生命科学、医学、气象学等领域［1-2］。面板数据的变点分析问题始于Joseph等人提出的随机变点模型［3-4］。Bai使用最小二乘法和拟极大似然方法估计了面板数据中均值与方差的共同变点，并得到了变点估计量的极限分布［5］。自Page 首次提出累积和（Cumulative Sum，CUSUM）方法对变点进行连续性检验后［6］，CUSUM 方法被许多统计学家改进并应用于变点的检测与估计。Horváth 等人在Bai的模型基础上，关于面板数据中均值是否存在共同变点提出了一个基于平方累积和（Squared CUSUM）的检验统计量，并在原假设H0（即没有变点）下得到了检验统计量的渐进分布［7］。Li等人和Shi分别使用CUSUM 方法［8］和似然方法［9］对面板数据中方差是否存在共同变点进行了检验。徐小平等人使用拟极大似然方法和CUSUM 方法对面板数据中方差的共同变点进行了估计，并结合二元分割法将其推广到多变点情形［10］。

这些关于面板数据变点分析的研究，当观测时长T较长，变点位置不在序列的端点附近时，即，估计都很有效，但对于观测时长T较短（即T＜30），或变点出现在序列端点附近时，估计的精度大幅降低。Horváth等人使用CUSUM方法对长相依序列中的变点进行估计时，在数值模拟过程中发现调节参数对变点估计的精确度有显著影响［11］。Chen 等人通过调节参数对面板数据中均值的共同变点提出了一个改进的CUSUM 型估计量，数值模拟给出了不同调节参数下变点估计的精确度［12］。谭常春等人研究了CUSUM 型统计量中调节参数对单变量序列中变点估计效果的影响［13］。文章通过调节参数对面板数据中方差的共同变点提出了一个改进的CUSUM 型估计量，研究调节参数γ∈(0,1) 对方差共同变点估计精确度的影响。蒙特卡洛模拟表明通过调节参数不仅使得变点位置在序列中间时得到很好的估计效果，而且使得变点位置在序列端点附近时，估计的精确度有了大幅度提升，并结合二元分割法将其推广到多个方差共同变点的情形。最后，应用2018 年1 月—2022 年12 月外汇汇率进行实证分析，结果表明调节参数（γ≠0）下CUSUM型估计方法是有效的。

1 模型与主要结果

考虑面板数据中方差的共同变点模型

其中，k0未知，Yit（i=1,2,…,N；t=1,2,…,T）是面板数据中第i个截面个体在t时刻的观测值，μi是第i个截面个体的均值，ηit是第i个截面个体在t时刻的误差项。在这个模型中，若σi1≠σi2，则未知时刻k0（1 ≤k0＜T）称为面板数据中方差的共同变点，即这N个截面个体方差的共同变点。当k0=T时，表明面板数据中不存在方差共同变点。令

其中，γ为调节参数，γ∈(0,1)，调节参数可以保证方差共同变点k0在靠近序列端点时估计的有效性，γ=0表示无调节参数。表示第i个截面个体在T个不同时刻得到观测值的样本均值。记=Yit-Yˉi，则为面板数据中心化后的结果，从而

为了估计方差的共同变点，需要下列假设条件:

假设1：E(ηit)=0，Var(ηit)=1，其中

假设2：存在正数M＞0，使得

假设3：存在τi∈(0,1)，ε＞0，使得ki=[Tτi]，并且τi+1-τi＞ε，i=0,1,2,…,m，其中[·]为取整函数；

假设4：表示方差跳跃度的平方，即方差的变化强度；

假设5：对任意的1 ≤k≤s≤T，都有，其中h∈(0,2)，注意在整篇文章中，正数C可能会不同，而且C与N和T是相互独立的；

假设6：存在α∈(0,1)，使得

注：假设1～假设3为Bai的研究中关于面板数据的假设，其中假设1能保证误差项ηit满足平稳性，假设2要求误差项ηit的四阶矩有限，假设3 确保了模型的每两个变点之间有足够多的样本，这是大数定律和中心极限定理成立的基本条件，通常ε取0.05，0.01 等较小的数。假设4 类似于Bai 的假设2，这个假设既保证方差变化强度δi的非负性，又合理描述截面个数N与方差变化强度δi之间的关系［5］。假设5满足常见的平稳序列或者非平稳序列，更多的案例参看文献［14］。假设6表示当N,T→∞时，Tα趋于无穷大的速度快于N.

引理1［14］设Y1,…,Yn是任意二阶矩有限的随机变量序列，C1,C2,…,Cn为任意的非负常数，则

定理1设面板数据模型（1）中存在一个方差共同变点若假设1～假设5 都成立，且则对于任意ε＞0，由式（3）定义的面板数据中方差的共同变点估计量τ0满足

推论1设面板数据模型（1）中存在一个方差共同变点若假设1～假设6 都成立，且则对于任意ε＞0，由式（3）定义的面板数据中方差的共同变点估计量τ0满足

2 结果的证明

定理1的证明当面板数据模型（1）中存在方差共同变点k0时，可知

3 面板数据中方差多变点的估计步骤

若模型（1）中存在m个变点，且变点个数m已知，则模型（1）转化为

再结合二元分割法将上述方法推广到多变点的情形，则模型（10）中的方差多变点估计具体步骤如下:

第一步：利用式（4）估计出第一个变点；

第二步：在处将整个面板数据一分为二，得到两个子样本，第一部分为Yi1,Yi2,…,Yi，第二部分为Yi,+1,Yi,+2,…,YiT，i=1,2,…,N，再利用式（4）分别估计这两个部分的变点

第三步：在前一部分面板数据中计算出

第四步：在后一部分面板数据中计算出

第五步：比较的大小，若

第六步：将进行排序，然后基于这两个变点将整个面板分成三个部分，类似第二、三、四步估计出第三个变点，重复使用上述方法，直至估计出m个变点。

4 数值模拟

应用MATLAB 软件，通过蒙特卡洛模拟研究调节参数γ的取值对面板数据中方差的共同变点估计精确度的影响。对于模型（1），简单起见，只考虑一个变点的情形，令ui=1，ηit～N(0,1)，σi1=0.1，σi2=0.2，这里方差跳跃度并不大。

首先，研究观察时长较短时的情况，取T=10，变点位置在端点附近及中间位置时，不同的截面个体数量（N=10、20、50、80、100、150、200、250、300）情况下，调节参数γ的取值对面板数据中方差的共同变点估计精确度的影响，MATLAB 模拟10000次。图1和图2分别展示了变点位置为k0=2和k0=9时，调节参数γ的取值对面板数据中方差的共同变点估计精确度的影响。γ=0表示无调节参数，这里“精确度”指的是数值模拟中变点估计量包含真实变点的频率，模拟结果表明调节参数（γ≠0）下CUSUM 型估计量的精确度高于无调节参数（γ=0）下CUSUM 型估计量的精确度，并且随着截面个体数量N的增加，精确度会大幅度上升。图3展示了变点位置在中间时（k0=5），调节参数γ的取值对面板数据中方差的共同变点估计精确度的影响，模拟结果表明调节参数（γ≠0）下CUSUM 型估计量的精确度与无调节参数（γ=0）下CUSUM 型估计量的精确度几乎相当，并且随着截面个体数量N的增加，精确度会大幅度上升，当N=150 时，调节参数（γ≠0）下CUSUM型估计量的精确度与无调节参数（γ=0）下CUSUM型估计量的精确度几乎都达到100%.

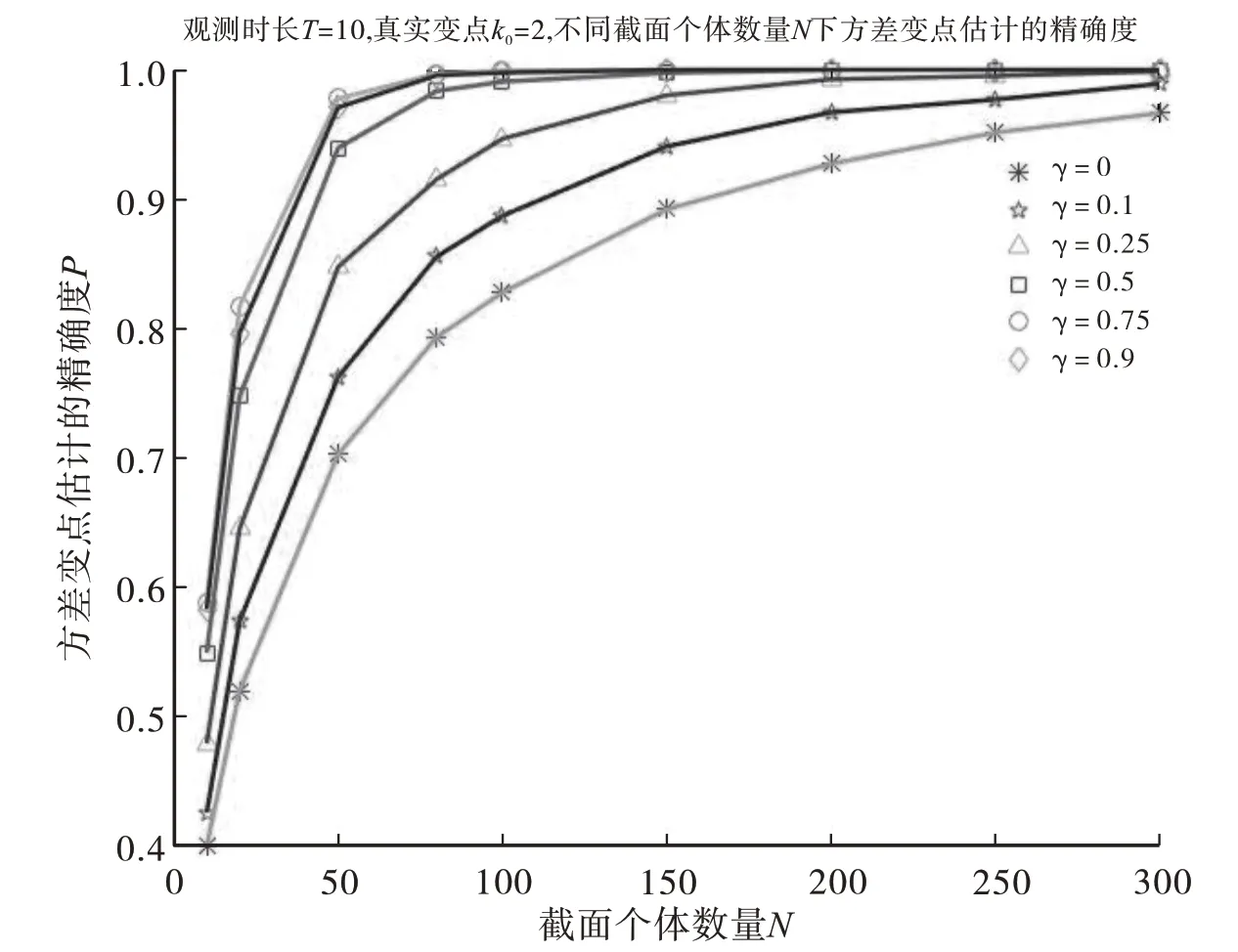
图1 不同的调节参数γ下CUSUM型估计量的精确度（T=10，左端变点k0=2）

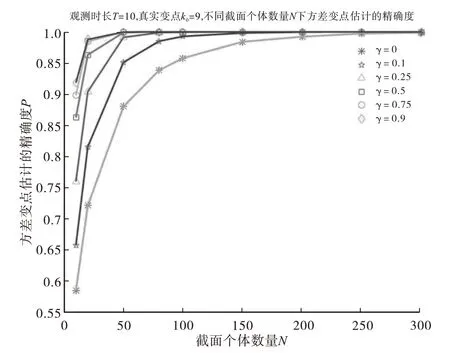
图2 不同的调节参数γ下CUSUM型估计量的精确度（T=10，右端变点k0=9）

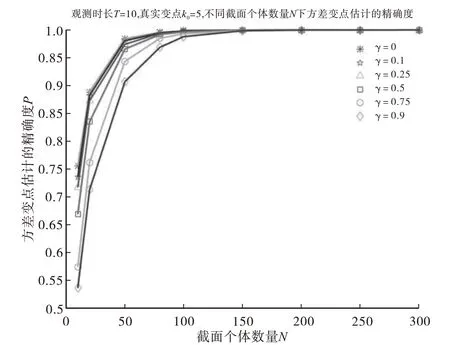
图3 不同的调节参数γ下CUSUM型估计量的精确度（T=10，中间变点k0=5）

其次，研究观察时长较长时的情况，取T=50，变点位置在端点附近及中间位置时，不同的截面个体数量（N=10、20、50、80、100、150、200、250、300）情况下，调节参数γ的取值对面板数据中方差的共同变点估计精确度的影响，MATLAB模拟10000次。图4和图5分别展示了变点位置为k0=2和k0=T-1时,调节参数γ的取值对面板数据中方差的共同变点估计精确度的影响，模拟结果表明调节参数（γ≠0）下CUSUM型估计量的精确度明显高于无调节参数（γ=0）下CUSUM 型估计量的精确度。图6 展示了变点位置在中间时（k0=T/2），调节参数γ的取值对面板数据中方差的共同变点估计精确度的影响，模拟结果表明调节参数（γ≠0）下CUSUM 型估计量的精确度与无调节参数（γ=0）下CUSUM 型估计量的精确度几乎相当，并且随着截面个体数量N的增加，精确度会大幅度上升，当N=100时，调节参数（γ≠0）下CUSUM型估计量的精确度与无调节参数（γ=0）下CUSUM型估计量的精确度几乎都达到100%.

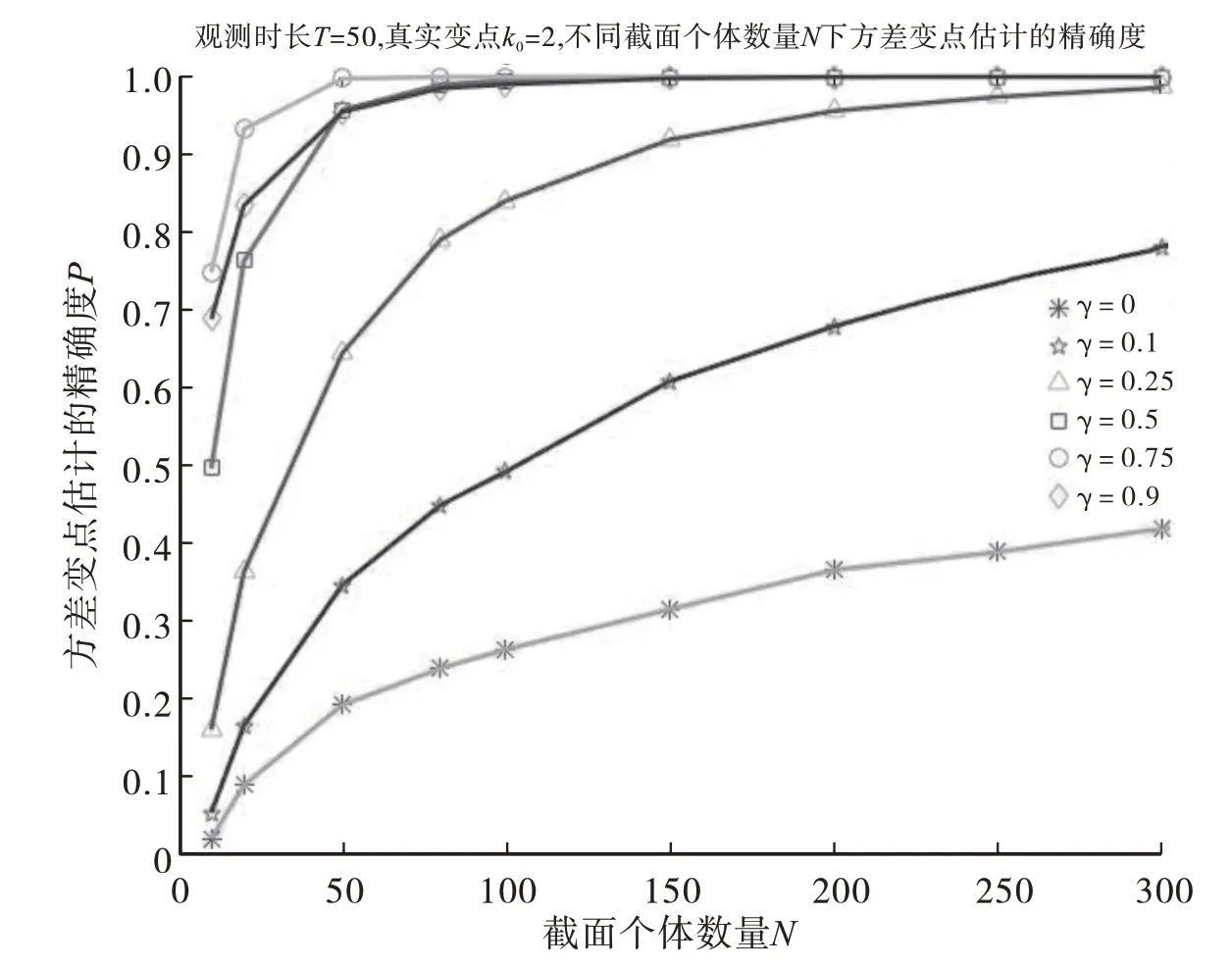
图4 不同的调节参数γ下CUSUM型估计量的精确度（T=50，左端变点k0=2）

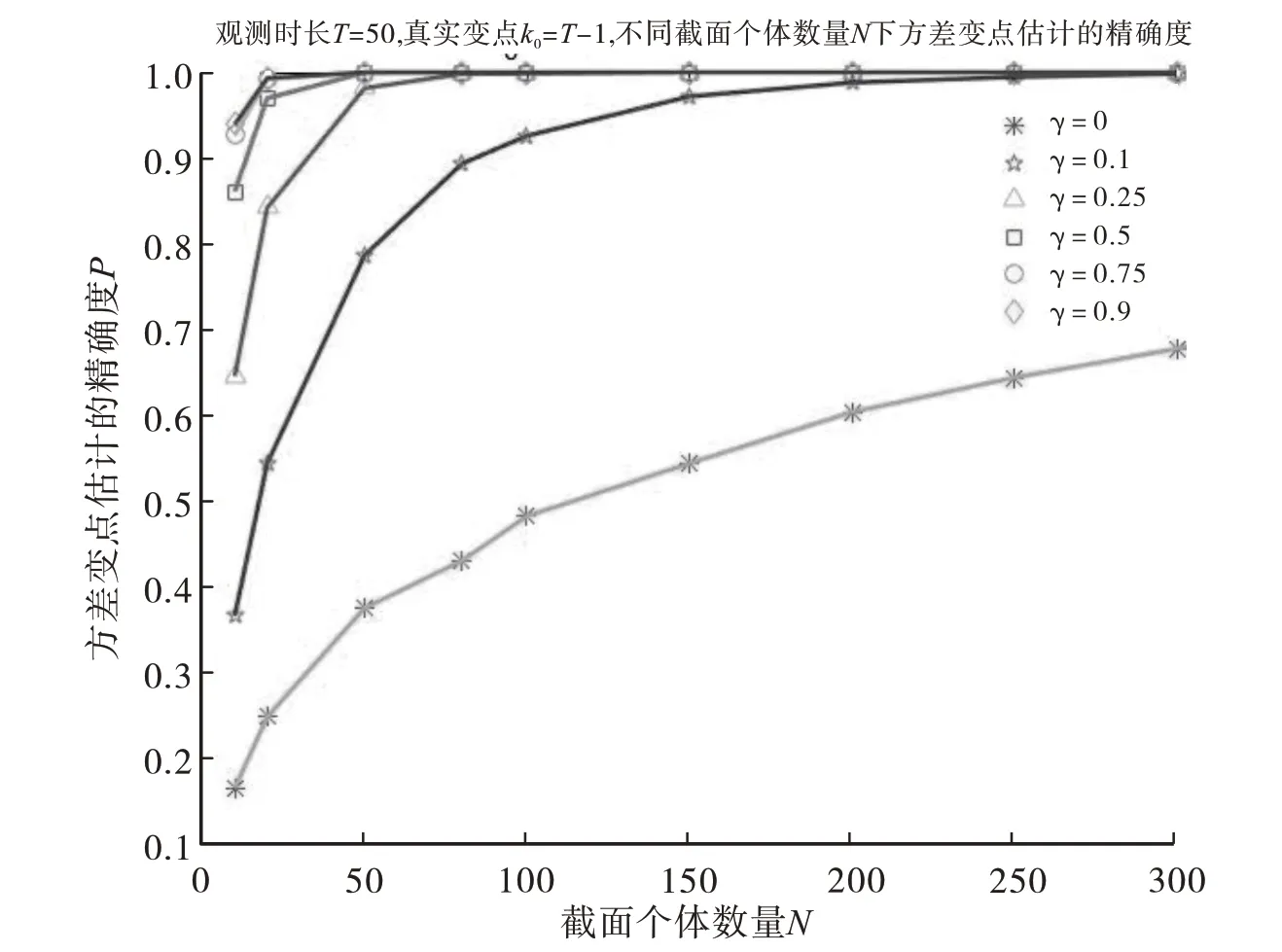
图5 不同的调节参数γ下CUSUM型估计量的精确度（T=50，右端变点k0=T -1）

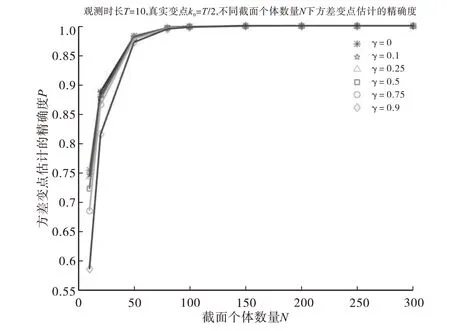
图6 不同的调节参数γ下CUSUM型估计量的精确度（T=50，中间变点k0=T/2）

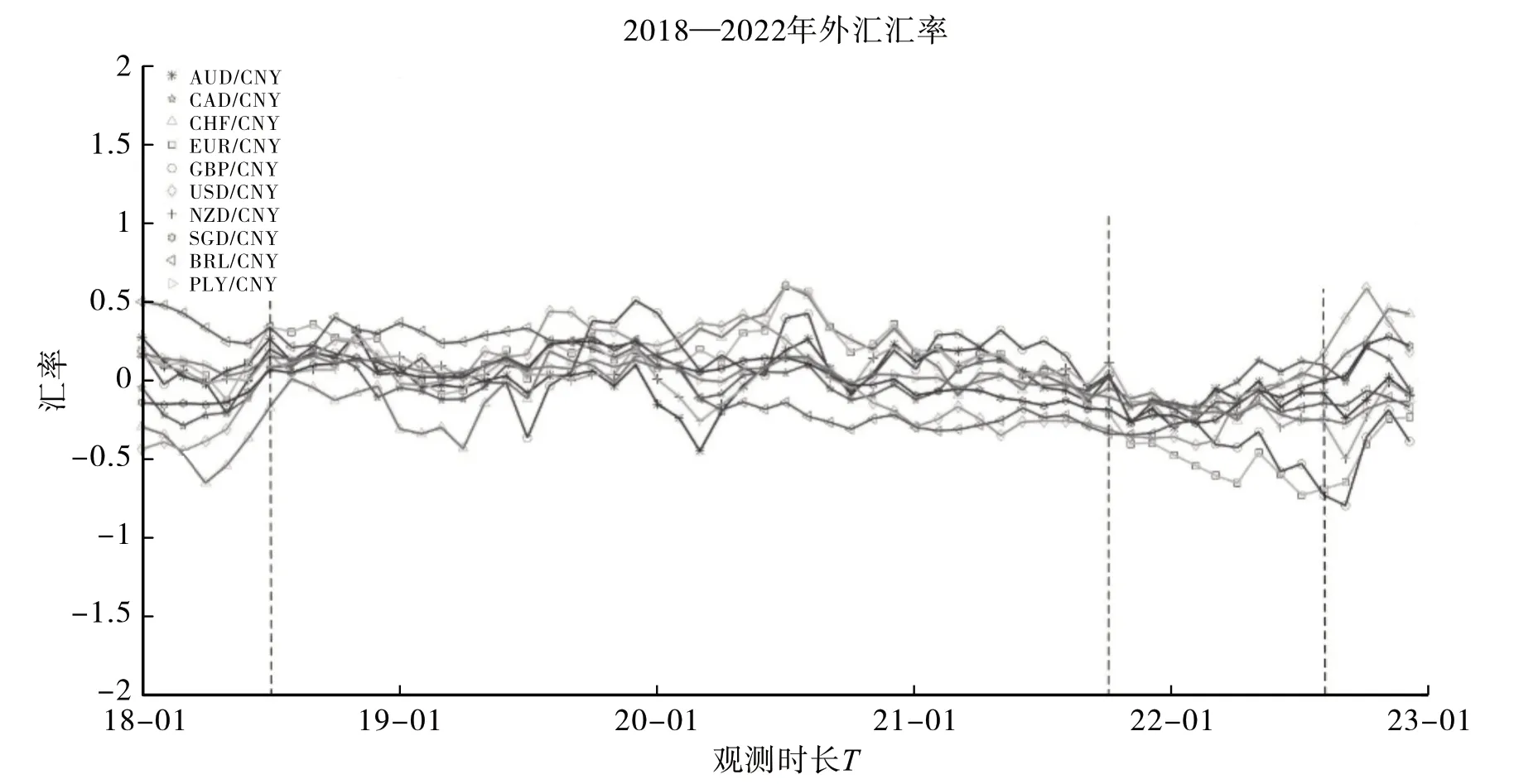
图7 10个国家的货币兑换人民币的外汇月度汇率数据图

综合分析，无论变点位置在中间还是端点附近时，调节参数（γ≠0）下CUSUM 型估计量都会有非常好的表现，这与前面的理论结果也相吻合。

5 实证分析

文章选取2018 年1 月—2022 年12 月10 个国家的货币（澳大利亚元（AUD）、加拿大元（CAD）、瑞士法郎（CHF）、欧元（EUR）、英镑（GBP）、美元（USD）、新西兰元（NZD）、新加坡元（SGD）、巴西雷亚尔（BRL）、波兰兹罗提（PLN））兑换人民币（CNY）的外汇月度汇率数据（数据来源于https://cn.investing.com/currencies/），共有10 个不同的截面个体，每个截面个体含有60 个历史数据，即N=10，T=60，首先对选取的数据进行去均值化处理，然后采用不同调节参数（γ=0.1,0.25,0.5,0.75,0.9）情况下CUSUM 型估计量的方法估计变点，估计的变点位置都是46，对应的实际时间是2021 年10 月。造成这种现象的原因主要是2021 年8 月国际货币基金组织（IMF）批准了史上规模最大的一轮新增特别提款权（SDR）分配计划。结合二元分割法，该变点将2018年1 月—2022 年12 月外汇汇率数据一分为二，采用上述方法分别对2018 年1 月—2021 年10 月和2021 年11 月—2022年12月数据进行变点估计。得到的变点位置为7（前一部分）和10（后一部分），对应的实际时间分别是2018年7月和2022年8月，前一部分变点出现主要与2018年6月美联储的加息政策以及央行的降准政策有关。后一部分变点出现主要与2022年8月美联储的加息政策以及国内经济复苏缓慢有关。

6 结论

文章通过调节参数对面板数据中方差的共同变点提出了一个改进的CUSUM 型估计量，研究调节参数对面板数据中方差的共同变点估计效果的影响，并结合二元分割法将其推广到多个方差共同变点的情形。模拟结果表明调节参数对面板数据中方差的共同变点估计有显著影响，同时发现此方法不仅适合样本小的面板数据，也适合样本大的面板数据，丰富了面板数据中方差的共同变点估计的研究方法。