Riesz模范畴的完备性和余完备性

李丹阳，汤建钢，2

（1.伊犁师范大学 数学与统计学院，新疆 伊宁 835000；2.伊犁师范大学 应用数学研究所，新疆 伊宁 835000）

自Birkhoff提出格序群［1］概念以来，序代数理论得到迅猛发展，Birkhoff等人研究了格序群的一般结构和分解理论，并将格序结构引入到环上，提出了格序环的相关概念［2］。Riesz将格序结构引入到向量空间，形成了Riesz空间的一些基础理论［3］。模作为域上线性空间概念的推广，已经成为当代重要的代数结构之一。崔晓宇等人在戴天佑研究的基础上将Riesz空间推广到左R-模上，定义了Riesz模的概念，讨论了左R-模上Riesz空间的相关性质，为左R-模上Riesz空间理论的研究奠定了基础［4-5］。孙锐娟等人在格序群、格序环以及格序结构Riesz空间概念的基础上，研究了左R-模上Riesz空间的同态与同构的相关性质［6］。刘晓芳等人在Riesz模范畴概念的基础上，研究了Riesz模簇的直积与直和，并对其相关性质进行了证明［7］。

范畴论是以抽象的方式处理数学结构并研究不同结构之间的联系而成为一个重要的现代数学基础理论。范畴的完备性和余完备性是两个重要的性质，张娟娟等人证明了Ω-左R-模范畴是完备的［10］，耿俊等人证明了Ω-Cat范畴是完备的［11］，徐晓泉证明了完全分配格范畴具有完备性和余完备性［13］。基于以上研究背景，文章讨论了Riesz模范畴中的乘积和余积、等值子和余等值子，进而证明了Riesz模范畴具有完备性和余完备性。

1 预备知识

定义1［9］设L为一个偏序集，如果对任意的a,b∈L，sup{a,b}与inf{a,b}均存在且都在L中，则称偏序集L是一个格，分别用a∨b与a∧b表示sup{a,b}与inf{a,b}，并且用四元序(L,≤,∨,∧)表示格，简记为(L,≤).

定义2［5］设(G,+)是一个Abel群，如果(G,+,≤)是一个格，且满足相容性条件，即对任意的a,b,c∈G，a≤b⇒a+c≤b+c，则称(G,+,≤)是一个Abel格序群，简称Abell-群。

定义3［5］设(R,+,·)是一个具有单位元的环，如果(R,+,·,≤)是一个格，且满足下列相容性条件，即对任意的r,s,t∈R:

（1）r≤s⇒t+r≤t+s；

（2）0 ≤r,0 ≤s⇒0 ≤rs；则称(R,+,·,≤)是一个格序环，简称l-环。

定义4［6］设M是左R-模，如果(R,+,·,≤)是具有单位元的l-环，(M,+,≤)是Abell-群，且满足下列相容性条件，即对任意的m,n,p∈M，r∈R:

（1）m≤n⇒p+m≤p+n；

（2）0 ≤r,0 ≤m⇒0 ≤rm；则称(M,+,≤)是一个格序左R-模，简称Riesz模。

定义5［6］设(M,+,≤)是Riesz模，N是M的子集，并且(N,+)是(M,+)的子模，(N,≤)是(M,≤)的子格，并且R+N+⊆N+，则称(N,+,≤)是(M,+,≤)的一个子Riesz模。

定义6［7］设M，M'都是左R-模，f:M→M'是映射，若对任意的r∈R，m,n∈M有

成立，则称f是R模同态，简称R同态。

定义7［9］设P、Q都是格，f:P→Q是映射，若对任意的x,y∈P有

成立，则称f是格同态。

定义8［5］设(M,+,≤)、(N,+,≤)均为Riesz模，f:M→N是映射，若f既是R模同态，又是格同态，则称f是Riesz模同态，记作f:(M,+,≤) →(N,+,≤).

定义9［7］Riesz模构成的范畴定义为:

（1）对象类ob()为全体Riesz模；

（2）对任意的(M,+,≤),(N,+,≤) ∈ob()，Hom((M,+,≤),(N,+,≤))={f|f:(M,+,≤)到(N,+,≤)的一个Riesz模同态}；

（3）若(M,+,≤),(N,+,≤),(P,+,≤) ∈ob()，f∈Hom((M,+,≤),(N,+,≤))，g∈Hom((N,+,≤)，(P,+,≤))，态射的复合gf∈Hom((M,+,≤),(P,+,≤))为同态的复合；

（4）对任 意的(M,+,≤) ∈ob()，单位态射为1M∈Hom((M,+,≤),(M,+,≤))，并且对任意的f∈Hom((M,+,≤),(N,+,≤))，g∈Hom((P,+,≤),(M,+,≤))，有f1M=f，1Mg=g.

定义10［14］设C是一个范畴，{Mi|i∈I}是C中的一簇对象，C中的对象M叫作{Mi|i∈I}的乘积，如果:

（1）对任意的i∈I，存在态射pi:M→Mi；

（2）对任意对象N∈C，若存在态射qi:N→Mi,i∈I，则存在唯一的态射α:N→M使得图1可交换。

图1 乘积的定义示意图

定义11［14］设C是一个范畴，{Mi|i∈I}是C中的一簇对象，C中的对象L叫作{Mi|i∈I}的余积，如果:

（1）对任意的i∈I，存在态射qi:Mi→L；

（2）对任意对象N∈C，若存在态射pi:Mi→N,i∈I，则存在唯一的态射β:L→N使得图2可交换。

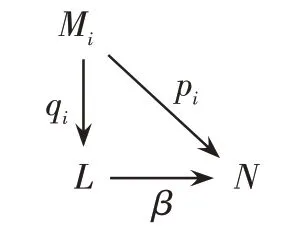
图2 余积的定义示意图

定理1如果(M,{pi}i∈I)和(M',{}i∈I)都是范畴C的对象簇{Mi|i∈I}的乘积，则M和M'是同构的。

证明由于M和M'都是范畴C中{Mi|i∈I}的乘积，那么对任意的i∈I，存在态射pi:M→Mi及:M'→Mi，又因为M和M'都是乘积，所以存在态射f:M'→M及g:M→M'使得图3可交换，故对任意的i∈I有，由i的任意性可知gf=1M'，同理可知fg=1M，所以M和M'是同构的。

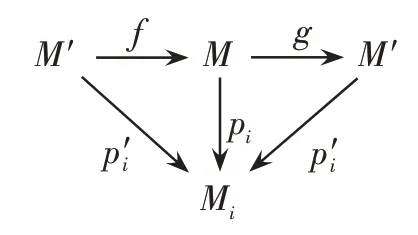
图3 乘积同构示意图

定理2如果都是范畴C的对象簇{Mi|i∈I}的余积，则L和L'是同构的。

注:定理1和定理2说明范畴的乘积或者余积如果存在，则在同构意义下均是唯一的。

定义12［14］设f，g:M→N是一对平行态射，如果态射e:E→M满足:

（1）fe=ge；

（2）对任意的态射e':E' →M满足fe'=ge'，存在唯一的态射h:E' →E使得e'=eh成立（图4），则称e:E→M是f,g:M→N的等值子。

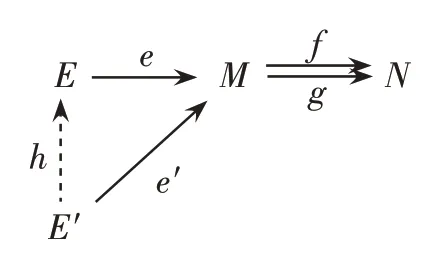
图4 等值子的定义示意图

定义13［14］设f,g:M→N是一对平行态射，如果态射q:N→L满足:

（1）qf=qg；

（2）对任意的态射q':N→L'满足q'f=q'g，存在唯一的态射π:L→L'使得q'=πq成立（图5），则称q:N→L是f,g:M→N的余等值子。

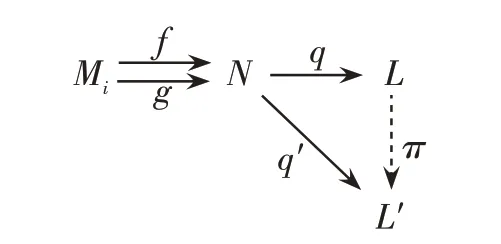
图5 余等值子的定义示意图

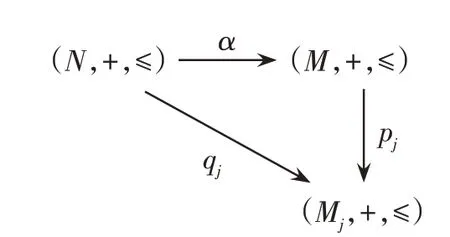
图6 Riesz模范畴中乘积示意图

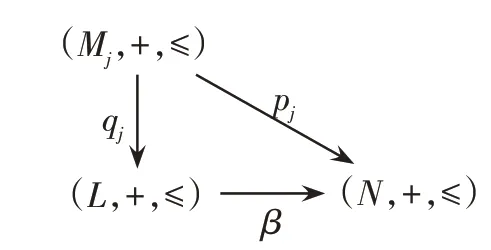
图7 Riesz模范畴中余积示意图

图8 Riesz模范畴中等值子示意图

图9 Riesz模范畴中余等值子示意图

引理1［14］设C是一个任意范畴，则C是完备的当且仅当存在乘积和等值子。

引理2［14］设C是一个任意范畴，则C是余完备的当且仅当存在余积和余等值子。

2 主要结果

下面讨论Riesz模范畴中的乘积与余积。

引理3设{(Mi,+,≤)|i∈I}是范畴中的一簇Riesz模，这里的指标集I是任意的，记(M,+,≤)=Π(Mi,+,≤)是Riesz模簇的笛卡尔积，其中(M,+,≤)中的元素表示为{mi|mi∈Mi}i∈I，在该集合中规定:对任意的{mi }，{m'i}∈(M,+,≤)，r ∈(R,+,·,≤)有

则

（1）(M,+,≤)是一个Riesz模；

（2）投影pj:(M,+,≤) →(Mj,+,≤)，pj({mi})=mj是Riesz模满同态。

证明（1）由模论可知，(M,+,≤)是一个左R-模。又由于{mi}∧{}={mi∧}以及{mi}∨{}={mi∨}，故(M,+,≤)可以构成一个格。并且对任意的{ni}∈(M,+,≤)，若{mi}≤{}，r≥0，那么有

故相容关系成立，由此可得(M,+,≤)是一个Riesz模。

（2）投影pj:(M,+,≤) →(Mj,+,≤)，pj({mi})=mj，显然pj是满射，对任意的{mi}，{}∈(M,+,≤)，r∈(R,+,·,≤)有

由此可得，投影pj:(M,+,≤) →(Mj,+,≤)是Riesz模满同态。

定理3设{(Mi,+,≤)}i∈I是范畴中的一簇Riesz模，作{(Mi,+,≤)}i∈I的笛卡尔积(M,+,≤)=Π(Mi,+,≤)，则{pj:(M,+,≤) →(Mj,+,≤)|j∈I}是对象簇{(Mi,+,≤)}的乘积。

证明设对任意的Riesz模(N,+,≤) ∈ob()，且存在Riesz模同态qj:(N,+,≤) →(Mj,+,≤)，定义α:(N,+,≤) →(M,+,≤)，其中∀n∈(N,+,≤)，α(n)={qi(n)}i∈I.易知α是一个映射，以下证明α是Riesz模同态:对任意的x,y∈(N,+,≤)，r∈(R,+,·,≤)有

故α是Riesz模同态。并且对任意的n∈(N,+,≤)，pjα(n)=pj{qi(n)}=qj(n)，故由n的任意性可得pjα=qj成立。又由于乘积在同构意义下是唯一的，所以{pj:(M,+,≤) →(Mj,+,≤)|j∈I}是对象簇{(Mi,+,≤)}i∈I的乘积。

引理4设{(Mi,+,≤)|i∈I}是范畴中的一簇Riesz模，这里的指标集I是任意的，记(L,+,≤)=⊕(Mi,+,≤)={{mi}∈⊕(Mi,+,≤)|{mi} 中只有有限个mi≠0 }，在该集合中规定:对任意的{mi}，{}∈(L,+,≤)，r∈(R,+,·,≤)有

则

（1）(L,+,≤)是一个Riesz模；

（2）嵌入qj:(Mj,+,≤) →(L,+,≤)，qj(mj)={mjδij}是Riesz模单同态，其中

证明（1）由模论可知，(L,+,≤)是一个左R-模。又由于，故(L,+,≤)可以构成一个格，并且对任意的{ni}∈(L,+,≤)，若{mi}≤{}，r≥0，那么有

故相容关系成立，由此可得(L,+,≤)是一个Riesz模。

（2）嵌 入qj:(Mj,+,≤) →(L,+,≤)，qj(mj)={mjδij}，显 然qj是单射，对任意的r∈(R,+,·,≤)有

由此可得，嵌入qj:(Mj,+,≤) →(L,+,≤)是Riesz模单同态。

定理4设{(Mi,+,≤)}i∈I是范畴中的一簇Riesz模，作{(Mi,+,≤)}i∈I的直和(L,+,≤)=⊕(Mi,+,≤)，则{qj:(Mj,+,≤) →(L,+,≤)|i∈I}是对象簇{(Mi,+,≤)}i∈I的余积。

证明设对任意的Riesz模(N,+,≤) ∈ob()，且存在Riesz模同态pj:(Mj,+,≤) →(N,+,≤)，定义β:(L,+,≤) →(N,+,≤)，其中∀{mi}∈(L,+,≤)，β({mi})=∑pi(mi).因为{ }mi中只有有限个mi≠0，所以∑pi(mi) 有意义，故β是(L,+,≤) 到(N,+,≤) 的一个映射。下 证β是Riesz模同态:对任意的{mi},{}∈(L,+,≤)，r∈(R,+,·,≤)有

故β是Riesz模同态。并且对任意的mj∈(Mj,+,≤)，βqj(mj)=β({mjδij})=pj(mj)，故由mj的任意性有βqj=pj成立。又由于余积在同构意义下是唯一的，所以{qj:(Mj,+,≤) →(L,+,≤)|j∈I}是对象簇{(Mi,+,≤)}i∈I的余积。

下面讨论Riesz模范畴中的等值子和余等值子。

引理5设f,g:(M,+,≤) →(N,+,≤) ∈Mor()，令E={m∈M|f(m)=g(m)}，则

（1）(E,+,≤)是(M,+,≤)的子Riesz模；

（2）嵌入映射e:(E,+,≤) →(M,+,≤)是Riesz模同态。

证明（1）对于0 ∈(M,+,≤)有f(0)=g(0)，所以0 ∈(E,+,≤)，显然∅≠E⊆M，即E是M的非空子集；因为f,g∈Mor()，故对任意的m1,m2∈(E,+,≤)，r∈(R,+,·,≤)有

成立，故m1∧m2，m1∨m2∈(E,+,≤)，所以(E,+,≤)是(M,+,≤)的子格。又对任意的p∈(E,+,≤)，若m1≤m2，r≥0，那么p+m1≤p+m2且rm1≥0 成立，故相容关系成立，由此可得，(E,+,≤)是(M,+,≤)的子Riesz模。

（2）因为(E,+,≤)是(M,+,≤)的子Riesz模，所以在Riesz模范畴中，嵌入映射e:(E,+,≤) →(M,+,≤)是Riesz模同态。

定理5设f，g:(M,+,≤) →(N,+,≤)是Riesz模范畴中的一对平行态射，令E={m∈M|f(m)=g(m)}是(M,+,≤)的子Riesz模，则包含态射e:(E,+,≤) →(M,+,≤)]是平行态射的等值子。

证明（1）fe=ge显然成立；

（2）存在性:设(E',+,≤)是一个Riesz模，且存在Riesz模同态e':(E',+,≤) →(M,+,≤)满足fe'=ge'.

定义函数h:(E',+,≤) →(E,+,≤)，其中对任意的x∈(E',+,≤)，h(x)=e'(x).因为fe'(x)=ge'(x)，所以e'(x) ∈(E,+,≤)，那么有e(h(x))=e(e'(x))=e'(x)成立。由于态射e'是Riesz模同态，即e'既是R模同态又是格同态，故对任意的x,y∈(E',+,≤)，r∈(R,+,·,≤):

所以，h是Riesz模同态。

唯一性:设h':(E',+,≤) →(E,+,≤)也是Riesz模同态，且eh'=e'，那么对任意的x∈(E,+,≤)，由于e(h(x))=e(e'(x))=e'(x)，故有e(h'(x))=h'(x)成立，又由eh'=e'有e(h'(x))=e'(x)，所以

故由x的任意性可知h'=h，所以e:(E,+,≤) →(M,+,≤)是平行态射f与g的等值子。

定义14设θ是Riesz模(M,+,≤)上的一个等价关系，若(M,+,≤)中的元素m与n具有关系θ，则记作m≡n(modθ).如果对任意的m,n,p,q∈(M,+,≤)，r∈(R,+,·,≤)，当m≡p(modθ)，n≡q(modθ)成立时，有

则称θ是Riesz模(M,+,≤)上的同余关系，称(M/θ,+,≤)={θ(m)|m∈M}为(M,+,≤)关于同余关系θ的商集。若定义映射q:(M,+,≤) →(M/θ,+,≤)满足q(m)=θ(m)，即把(M,+,≤)中的元素m映射到m的等价类θ(m)，这样的映射称为自然映射。

引理6Riesz模(M,+,≤)上的任意多个同余关系的交仍为同余关系。

证明设{θi|i∈I}为Riesz模(M,+,≤)上的一簇同余关系，这里的指标集I是任意的。由θi是Riesz模(M,+,≤)上的等价关系可以验证∩θi为等价关系。事实上，

①自反性:对任意的m∈(M,+,≤)有(m,m) ∈∩θi(i∈I)，故(m,m) ∈∩θi.

②对称性:对任意的m,n∈(M,+,≤)，若(m,n) ∈∩θi，则对任意的θi(i∈I)有(m,n) ∈θi，从而(n,m) ∈θi，所以(n,m) ∈∩θi.

③传递性:对任意的m,n,p∈(M,+,≤)，若(m,n) ∈∩θi，(n,p) ∈∩θi，则对任意的θi(i∈I)有(m,n) ∈θi，(n,p) ∈θi，从而(m,p) ∈θi，所以(m,p) ∈∩θi.

以下证明θi是Riesz模(M,+,≤)上的同余关系:对任意的m,n,p,q∈(M,+,≤)，r∈(R,+,·,≤)，若(m,p) ∈∩θi，(n,q) ∈∩θi，则对任意的θi(i∈I)均有(m,p) ∈θi，(n,q)∈θi，所以有

从而

所以∩θi是Riesz模(M,+,≤)上的同余关系。

引理6设θ是Riesz模(N,+,≤) 中 的Riesz模同余关系，在Riesz模(N,+,≤) 关 于θ的 商N/θ={θ(n)|n∈N}中规定:对任意的n1,n2∈(N,+,≤)，r∈(R,+,·,≤)有

则

（1）N/θ,+,≤)是一个Riesz模；

（2）自然映射q:(N,+,≤) →(N/θ,+,≤)是Riesz模同态。

证明（1）首先证明“运算与代表元的选取无关”。对任意的满足，即那么由

可知，该运算与代表元的选取无关。

其次证明(N/θ,+,≤)是一个Abell-群:

①结合律:对∀θ(n1),θ(n2),θ(n3) ∈(N/θ,+,≤)，满足

②单位元:对∀θ(n) ∈(N/θ,+,≤)，存在θ(0) ∈(N/θ,+,≤)使得θ(n)+θ(0)=θ(n+0)=θ(n)，故单位元存在。

③逆元:对∀θ(n) ∈(N/θ,+,≤)，存在θ(-n) ∈(N/θ,+,≤)使得θ(n)+θ(-n)=θ(n-n)=θ(0)，故逆元存在。

④交换律:对∀θ(n1),θ(n2) ∈(N/θ,+,≤)，满足

⑤相容性:对∀θ(n1),θ(n2),θ(p) ∈(N/θ,+,≤)，θ(n1)≤θ(n2)有θ(p)+θ(n1)=θ(p+n1)≤θ(p+n2)=θ(p)+θ(n2)，故满足相容性条件。

以下证明(N/θ,+,≤)是一个Riesz模。由模论可知(N/θ,+,≤)是一个左R-模。事实上，N/θ={θ(n)|n∈N}是一个Abel群，且满足以下性质:

①∀r∈(R,+,·,≤)，∀θ(n) ∈(N/θ,+,≤)有:rθ(n)=θ(rn) ∈(N/θ,+,≤)；

②∀r1,r2,r∈(R,+,·,≤)，∀θ(n1),θ(n2),θ(n) ∈(N/θ,+,≤)有

③∀r1,r2∈(R,+,·,≤)，∀θ(n) ∈(N/θ,+,≤)有

又由于对任意的θ(n1),θ(n2),θ(n3) ∈(N/θ,+,≤)满足:

①幂等律:θ(n1) ∧θ(n1)=θ(n1∧n1)=θ(n1)，θ(n1) ∨θ(n1)=θ(n1∨n1)=θ(n1)

②交换律:θ(n1) ∧θ(n2)=θ(n1∧n2)=θ(n2∧n1)=θ(n2) ∧θ(n1)

③结合律:θ(n1) ∧(θ(n2) ∧θ(n3))=θ(n1) ∧(θ(n2∧n3))=θ(n1∧(n2∧n3))=θ((n1∧n2) ∧n3))=θ(n1∧n2) ∧θ(n3)=(θ(n1) ∧θ(n2)) ∧θ(n3)

④吸收律:θ(n1) ∨(θ(n1) ∧θ(n2))=θ(n1) ∨(θ(n1∧n2))=θ(n1∨(n1∧n2))=θ(n1)

所以(N/θ,+,≤)是一个格。又对任意的θ(p)∈(N/θ,+,≤)，若θ(n1)≤θ(n2)，r≥0，那么有

故相容关系成立，由此可得(N/θ,+,≤)是一个Riesz模。

（2）自然映射q:(N,+,≤) →(N/θ,+,≤)，q(n)=θ(n)，∀n∈(N,+,≤).对任意的n1,n2∈(N,+,≤)，r∈(R,+,·,≤)有

成立，由此可得，q是Riesz模同态。

定义15设(M,+,≤)是一个Riesz模，R⊆M×M是M上的一个二元关系，令=∩{θ|R⊆θ，θ是M上的同余关系}，根据引理6，是(M,+,≤)上的同余关系，称为由R生成的最小同余关系。

定理6设f,g:(M,+,≤) →(N,+,≤)是Riesz模范畴中的一对平行态射，θ是Riesz模(N,+,≤)上包含{(f(m),g(m))|m∈M}的最小同余关系，则自然商同态q:(N,+,≤) →(N/θ,+,≤)是平行态射的余等值子且q(n)=θ(n).

证明（1）根据引理6，因为(N/θ,+,≤)是Riesz商模(N/θ,+,≤)={θ(n)|n∈N}，其中θ(n)是n的同余类，所以对任意的m∈(M,+,≤)，有q(f(m))=θ(f(m))，q(g(m))=θ(g(m))，又由于(f(m),g(m)) ∈θ，所以θ(f(m))=θ(g(m))，故q(f(m))=q(g(m))，则由m的任意性可知qf=qg成立。

（2）存在性:设(L,+,≤)是Riesz模，并且存在Riesz模同态q':(N,+,≤) →(L,+,≤)使得q'f=q'g.定义π:(N/θ,+,≤) →(L,+,≤)，其中∀n∈(N,+,≤)，π(θ(n))=q'(n)，那么π(q(n))=π(θ(n))=q'(n).因为对任意的n，n'∈(N,+,≤)，若n=n'，则有q'(n)=q(n')成立，那么对任意的θ(n)，θ(n')∈(N/θ,+,≤)，若θ(n)=θ(n')，则π(θ(n))=q'(n)=q'(n')=π(θ(n'))，所以π是映射。以下证明π是Riesz模同态。

首先对任意的x,y∈(N,+,≤)，r∈(R,+,·,≤):有

故θ是Riesz模同态。

唯一性:假设存在π':(N/θ,+,≤) →(L,+,≤)使得π'q=q'，由于对∀n∈(N,+,≤)有q(n)=θ(n)且π(θ(n))=q'(n)，则有π(q(n))=π(θ(n))=q'(n).因此

即π'(q(n))=π(q(n))，由n的任意性可知，π'=π.

综上可知，存在唯一的态射π:(N/θ,+,≤) →(L,+,≤)使得q'=πq成立，所以q:(N,+,≤) →(N/θ,+,≤)是平行态射的余等值子。

定理7Riesz模范畴是完备范畴。

证明由定理3和定理5可知，Riesz模范畴存在乘积和等值子，故由引理1可知，Riesz模范畴是完备范畴。

定理8Riesz模范畴是余完备范畴。

证明由定理4和定理6可知，Riesz模范畴存在余积和余等值子，故由引理2可知，Riesz模范畴是余完备范畴。