PID控制的阀控缸系统的Modelica建模与仿真实现

王瑞，梁全

（沈阳工业大学机械工程学院，沈阳 110870）

0 引言

在计算机辅助生产制造为主流的现代，对于实际工程中的液压系统来说，如果想要对其进行试验分析的话，最普遍的方法就是利用工业仿真软件对其进行模拟。而市面上的大多数涉及到液压系统的仿真软件都具有非常昂贵的采购价格，例如Matlab中的Simulink、AMESIM、20-sim、MWorks等[1-2]。而PID控制的阀控缸系统则是最为常见的一种液压伺服系统，几乎在所有的液压相关工程中都有所应用。但如果使用价格昂贵的商业仿真软件来对其进行仿真建模的话，在实际工程中存在仿真成本过高的问题。因此本文在开源仿真环境OpenModelica中开发了一套完善的PID控制的阀控缸系统模型，且该模型中的各个组成子模型均具有良好的模型复用性，不仅解决了实际工程中仿真成本过高的问题，还可以为想要利用Modelica语言建立液压系统模型的开发者们提供指导与借鉴。

1 Modelica语言

Modelica语言是在一种为了统一多领域物理系统的建模语言而设计的通用的面向对象的建模语言。在Modelica语言中，将涵盖多领域的物理系统的动态特性通过微分方程或者微分代数方程来描述，通过求解这些微分方程组或者微分代数方程组就可以实现物理系统的仿真并对其进行动态特性分析[3]。与利用赋值语句来描述物理系统的建模语言相比，Modelica这种利用数学方程式描述物理系统的语言具有不需要考虑数据流方向的非因果特点[4]。这使得利用Modelica语言编写的程序在形式上更为直观和规范。

2 数学模型

对于PID控制的阀控缸系统来说，主要由PID控制器、比例换向阀、液压缸、位移传感器、液压源及负载等部分组成[5]。这些部分的连接与相互作用关系如图1所示。

图1 PID控制的阀控缸系统框图

在对该系统建立Modelica模型之前，首先需要弄清楚系统各个部分的数学模型。对于PID部分来说，其数学模型[6]一般为

式中：u（t）为控制的输出信号，e（t）为输入偏差，Kp为增益，Ti为积分部分的时间常数，Td为微分部分的时间常数。

对于比例换向阀来说，从模型的复用性角度出发，可将其数学模型考虑为3个部分：输入限制部分、阀芯动态特性部分及换向阀通路部分。输入限制部分用于控制换向阀的输入电流不超过其预先设置的额定电流。该部分的数学模型为：

式中：ylim与ulim为输入限制部分的输入和输出，Irate为额定电流值。

换向阀的阀芯动态特性一般可以考虑为静态、一阶系统或者二阶系统，受篇幅限制，这里仅给出将阀芯考虑为二阶系统的情况。则其数学模型为

式中：ysec与usec为二阶系统的输入和输出，K为放大系数，ξ为阻尼，ωn为自然频率。

换向阀的通路部分可以考虑为由若干可变液压阻性元件构成，其数学模型[6]为：

式中：q为流过该通路的流量，Cq为流量系数，Cqmax为最大流量系数，A为液阻的最大有效面积，D为孔口直径，opening为液阻的开度分数，dp为液阻两端的压力差，ρ为油液密度，v为运动黏度，λ为临界流量系数。

对于开度分数来说，其与通路部分的输入u遵循如下关系：

式中，关于u的函数为换向阀阀口开度规律的定义，比如对于三位四通O型换向阀来说，有：

对于液压缸来说，同样从模型的复用性角度出发，可以将其数学模型考虑为液动力转换部分、容腔部分、泄漏部分及活塞部分的组合[7]。对于液动力转换部分来说，其功能主要是完成液动力向机械力的转换，该部分的数学模型为：

式中：p为液体压力，q为流量，V为腔室的体积，Vdead为腔室的死容积，s为位移，A为工作面积，F为液体压力产生的作用力。

可以将容腔部分考虑为液压容性元件，其数学模型为

式中，E为油液的体积模量。

可以将泄漏部分考虑为一个压力差与流量成线性关系的阻性元件。其数学模型为

式中：qleak为泄漏流量，dp为压力差，k为流量压力梯度（泄漏系数）。

活塞部分可以考虑为一个带有行程限位的机械移动惯性元件，并且在其数学模型中还考虑了相关摩擦[8]。其数学模型为

式中：FLoad为负载力，Ff为相关摩擦力。

当活塞正向运动时，有

当活塞反向运动时，有

式中：Fprop为速度相关阻尼，Fcoulomb为库伦摩擦力，Fstribeck为stribeck效应产生的摩擦力。

3 阀控缸系统建模

根据上述阀控缸系统各个组成部分的数学模型，即可利用Modelica语言在开源环境OpenModelica中建立阀控缸系统各个组成部分的子模型，然后对这些子模型建立正确的连接关系，则可得到阀控缸系统的整体模型[9]。这样就能使模型的重用性得到保证。

对于换向阀部分，首先根据式（2），利用Modelica语言建立换向阀输入限制部分的模型，如图2所示。

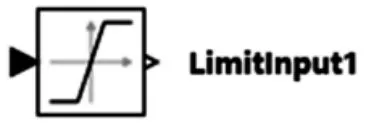
图2 换向阀输入限制部分的模型

然后根据式（4）、式（5）、式（6）建立可变液阻元件的模型，如图3所示。对于换向阀阀芯部分的二阶系统，则可以使用Modelica标准库中的二阶系统模型。

图3 可变液阻元件（换向阀通路）的模型

则使用上述子模型组成的三位四通O型比例换向阀模型的内部模型，如图4所示。

图4 三位四通O型换向阀的内部模型

在该模型中应用了4个液压阻性元件的模型，分别用来表示换向阀在左位和右位时通路的情况。所建立的换向阀模型如图5所示。

图5 三位四通O型换向阀的模型

对于液压缸部分，首先根据式（7）建立液压缸液动力转换部分的模型，如图6所示。然后根据式（8）建立容腔部分的模型，如图7所示。再根据式（9）建立泄漏部分的模型，如图8所示。

图6 液压缸动力转换部分的模型

图7 容腔部分的模型

图8 泄漏部分的模型

对于活塞部分，可以使用Modelica标准库中的带有行程限位及摩擦的质量块模型。使用上述子模型组成的液压缸模型的内部模型如图9所示。所建立的液压缸模型如图10所示。

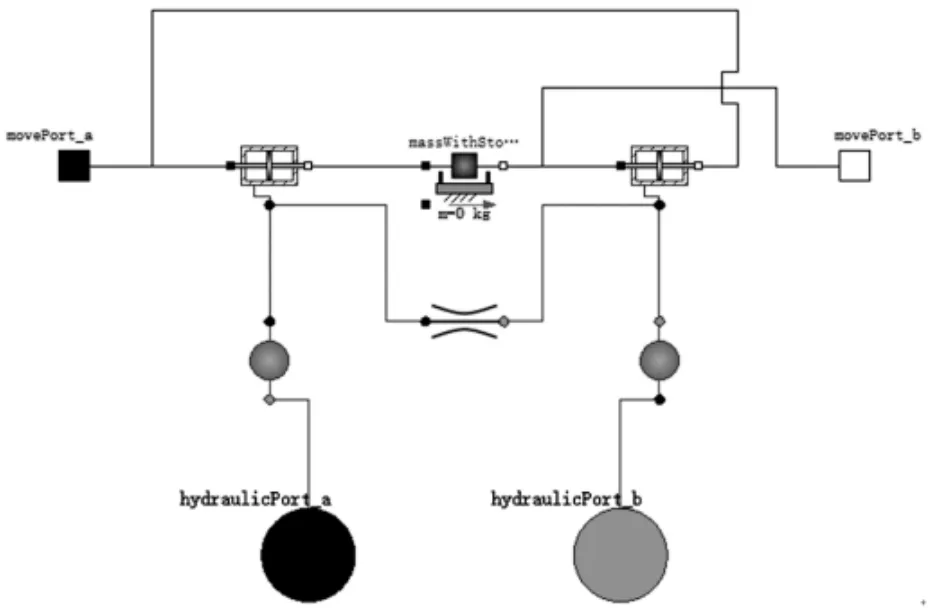
图9 液压缸的内部模型

图10 液压缸的模型

最后利用上述液压元件的模型并参考图1，即可在OpenModelica中建立PID控制的阀控缸系统的整体仿真模型，如图11所示。

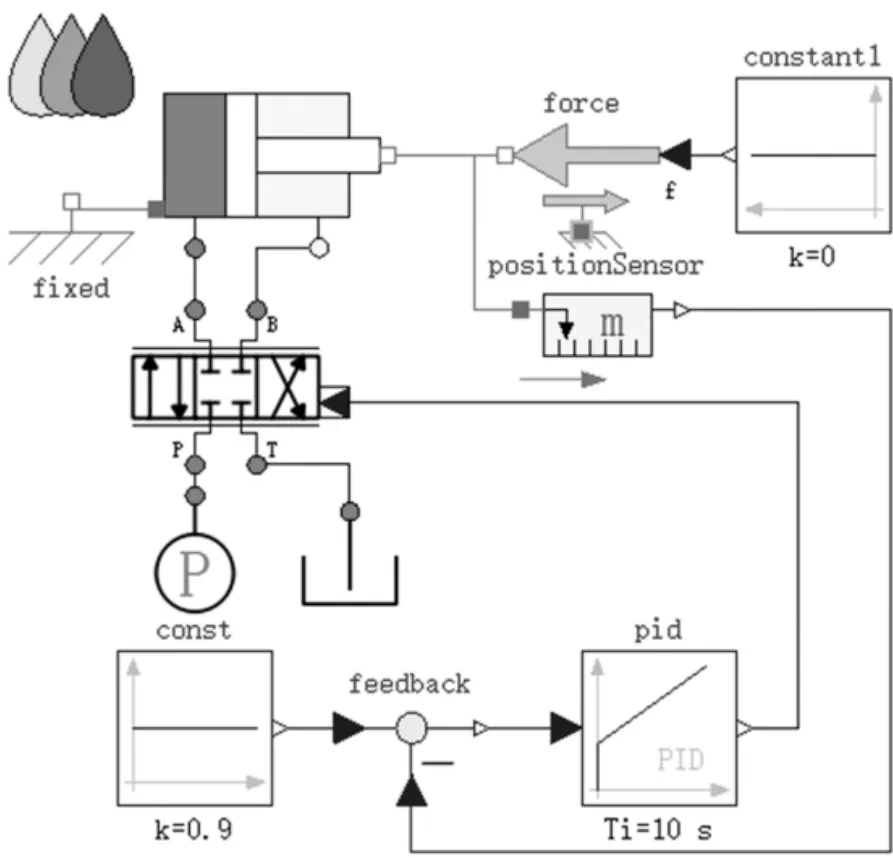
图11 PID控制的阀控缸系统的模型

4 仿真结果分析

PID控制的阀控缸系统主要参数如表1所示。

表1 主要仿真参数表

为了证明上述模型的正确性，本文设计了一个仿真结果对比实验，其方法是：在另一款行业内认可度较高的软件AMESIM中建立相同回路，并通过对比相同参数下二者的仿真结果来验证所建立的PID控制的阀控缸系统Modelica模型的正确性。有一点值得注意的是，在AMESIM中的PID控制器与Modelica中的PID控制器在参数设置上有所区别。在Modelica中PID模型的参数为k、Ti、Td及Nd[9]。而在AMESIM中则有kp、ki、kd及tau。二者的对应关系如下所示：

知道了上述关系后，为了便于理解，这里以AMESIM中的参数为标准来设置参数。当PID的参数设置如表2所示时，得到二者的液压缸活塞位移及速度的对比结果如图12、图13所示。

表2 PID参数表

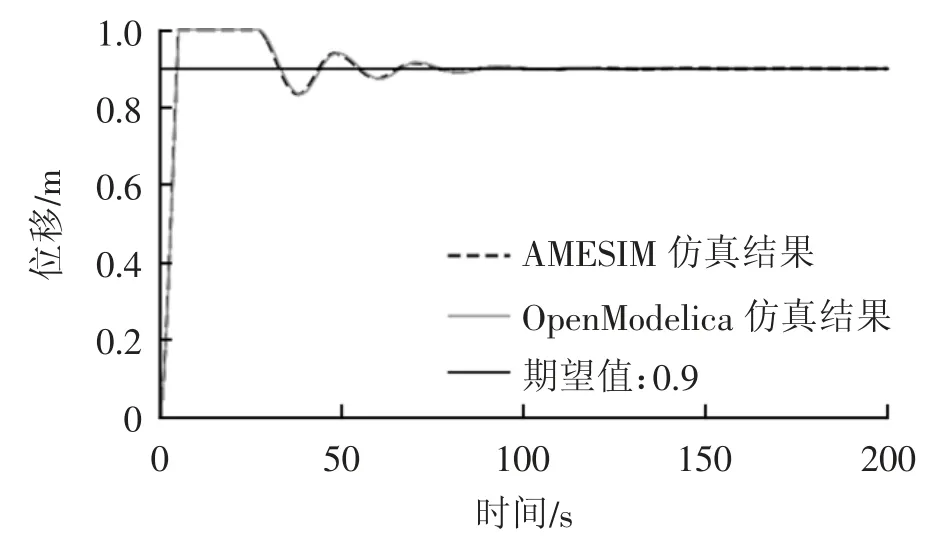
图12 液压缸活塞位移变化曲线

图13 液压缸活塞速度变化曲线

通过图像对比，不难看出二者的结果基本一致，且超调量不会超过液压缸的行程限位。所以可以证明本文所建立的PID控制的阀控缸系统的模型是正确的。接下来，通过调整PID的参数以验证该系统是否符合PID控制的规律。由于在表2所示参数的控制下该系统出现了振荡及超调现象，所以为了减弱系统的振荡现象应该减少ki的值，可将其值改为1且保持其余参数不变。则位移曲线变为图14中的曲线2。观察曲线2发现虽然系统的振荡减弱了，但是系统的响应时间变长了，所以还要增加kp的值，将其值改为100后则位移曲线变为图14中的曲线3。观察曲线3可以发现，不仅系统响应时间变短，而且振荡与超调得到了明显的改善。说明该系统的模型符合PID控制的规律，进一步证明了本文所建立的系统的正确性。

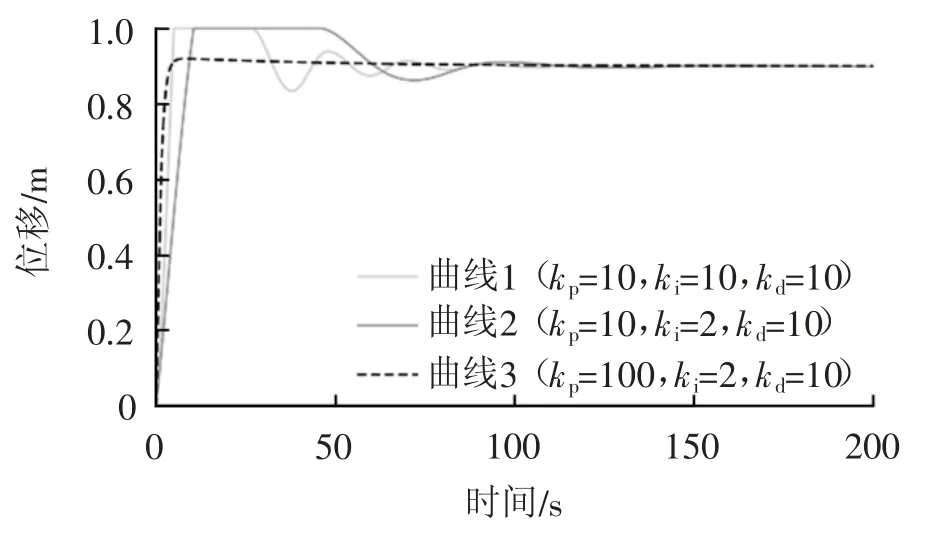
图14 不同PID参数下的活塞位移变化曲线

5 结论

通过利用Modelica 语言在开源仿真环境OpenModelica中开发了PID控制的阀控缸系统的仿真模型，并与AMESIM中所建立的相同系统模型的仿真结果做了对比与分析，得到了如下结论：1）本文所建立的PID 控制的阀控缸系统可以得到与AMESIM相同的仿真结果，并由于其是在开源环境下进行的建模，所以在实际工程中可以代替价格昂贵的商业仿真软件，可以对阀控缸系统进行仿真分析，大大节约了仿真建模的成本。2）本文所建立的系统模型的仿真结果可以通过调节PID的参数来得到有效的控制，符合PID控制的规律。且该系统的各级子模型均可重复使用。