云存储中基于压缩感知和生命游戏的图像数据保护算法

熊冰冰,温文媖,方玉明,张玉书

1(江西财经大学 信息管理学院,南昌 330000)

2(南京航空航天大学 计算机学院,南京 210000)

0 引 言

云存储是云计算的数据存储基础设施,为科研所、政府、企业和个人用户提供数据存储服务,用户可以按需获取数据,是一种便捷的数据存储服务.在云存储广泛应用的同时,所带来的问题也日益凸显:1)大量携带用户隐私信息的图像数据存储在云端中,用户隐私数据存在泄露隐患;2)由于传感器和移动设备等资源有限,面对需要接收的巨大数据量,实现低成本采样和传输的需求显得十分迫切.随着云存储图像规模的增长,隐私泄露逐渐频繁.许多好莱坞明星存储于云端的私人图像曾被黑客泄露,除此之外,Facebook曾被多次曝光窃取用户图像数据[1,2].

图像加密技术是防止图像数据泄露的有效手段之一,主要通过密钥将传输的图像信息转为密文,人眼通过密文不能直接获取有效信息,有效降低图像信息被窃取转而为他人所利用的概率,进而保护其在传输过程中的安全.混沌加密作为最常见的图像加密技术,主要利用混沌系统的一些基本特征,如遍历性(Ergodicity)、混合性(Mixing)、确定性(Exactness)、对初始条件的敏感性(Sensitivity)和吻合于密码学中的两个基本原则:混乱(Confusion)和扩散(Diffusion).混沌图像加密主要是在加密构架下,利用混沌系统产生的序列控制块图像、行和列像素位置或者比特面的分布以及扩散对应的像素值.大量研究表明,利用混沌能很好地解决图像加密领域的一些问题[3-6].Zhuang等人[7]提出基于新的五维多环多翼超混沌系统的图像加密算法,通过混沌序列,对明文图像矩阵进行置乱和异或运算,得到最终密文图像.针对图像加密,该算法有较好的加密效果.

然而与文本信息相比,图片和视频数据需要占据较大的存储空间,加密它们需要更多的计算量以及时间,加密效率相对下降.压缩感知(Compressed Sensing,简称CS)技术,即同时对信号进行采样和压缩操作[8-10].为保护图像数据的机密性,Huang等人[11]提出用于图像安全的压缩扩散置换策略,该策略使用压缩感知技术压缩图像,通过迭代二维正弦逻辑调制图构造测量矩阵,采用异或和扩散操作,增强策略安全性.Wen等人[12]针对感知加密图像的视觉安全措施,构建感知加密光场图像数据库,提出一种新的视觉安全性评估方法.Chai等人[13]结合压缩感知和最低有效位,提出高效的图像压缩和解密方案.对于已知明文和选择明文攻击,该算法具有鲁棒性.值得一提的是,压缩感知技术虽然是有损压缩,但人们可以接受具有一定程度失真的图像.Chen等人[14]提出新的矩阵乘法—半张量积(Semi-tensor product),能够实现前边矩阵列数和后边矩阵行数不等时的矩阵乘法运算.基于这样的性质,半张量积为实现不同阶的高维矩阵数字信号处理提供解决思路.Xie等人[15]证明半张量积能用于压缩感知,可以提高内存使用率和节省测量矩阵的存储空间.Wen等人[16]提出一种基于半张量积的CS策略,结合Arnold置乱和秘密图像的视觉安全策略,使该算法在减少测量矩阵占用空间的同时,恢复图像仍保有较高的重建质量.受此工作的启发,本文结合压缩感知和半张量积,减小测量矩阵的存储量,极大地节省传输端的存储空间.

元胞自动机,即由一系列元胞所组成的空间模型,主要包括元胞、元胞空间和规则等,是一种简单的计算方式,在一定规则下,元胞的变化难以预测,因此基于元胞自动机的图像加密算法可以隐藏明文图像信息,能够很好地保护用户图像数据,在密码学领域中被广泛应用[17,18].Ji等人[19]提出基于多重元胞自动机的图像水印加密算法,利用不同的元胞自动机规则逐级加密,有效克服基于直方图平移类可逆水印算法在安全性方面的不足,具有较高的安全性能.元胞自动机中最典型的是生命游戏,它由无数个局部变化过程组合而成,在变化过程中,简单图像可以变复杂,复杂图像也可以不断简化.

基于以上分析,本文结合半张量积-压缩感知和生命游戏,提出一种基于云存储的图像数据保护方案.本方案的创新性与优势在于:1)利用半张量积运算生成高维矩阵,输入端可以通过两个低阶矩阵获得高阶矩阵,再与图像数据信号进行矩阵相乘,节省图像加密过程中所需的存储空间,提升数据传输速率;2)高维的混沌系统所使用的参数更多,密钥空间大,抵抗暴力攻击的能力更强;3)初始细胞矩阵会随着明文图像的改变而发生变更,加强图像数据在传输过程中的隐私保护.实验表明,本方案能够用于云存储,并且在一定资源的条件下,能够实现图像数据安全和高效的传输.

1 相关工作

1.1 生命游戏规则

生命游戏(Game of life,简称GOL)是一种元胞自动机,由二维细胞矩阵组成.用0和1表示细胞的两种状态,0表示细胞是活的,1表示细胞是死的.细胞分布在网格内,根据细胞的局部空间形态决定细胞下一刻的生命状态.细胞之间的相互作用规则如下:

1)当细胞周围少于两个活细胞,任何活细胞都会死亡;

2)当细胞周围的活细胞是两个或3个时,任何活细胞都是活的;

3)当细胞周围刚好存在3个活细胞,任何死细胞都会变为活细胞;

4)当细胞周围存在3个以上的活细胞时,任何活细胞都可能死亡;

5)细胞的局部空间形态指的是由细胞和与它相邻的8个邻居细胞组成的空间形态.

生命游戏具有组成结构简单和组成单元之间复杂的动力学特性,本文利用生命游戏规则生成置乱矩阵,并用它作用图像的稀疏矩阵.基于细胞状态的变化性,可以隐藏明文图像信息,能够很好地保护用户图像数据.

1.2 五维忆阻混沌系统

相比于低维混沌系统,基于高维混沌系统的加密算法安全性更高,密钥空间也显著增大.闵富红等人[20]设计的五维忆阻混沌系统.

(1)

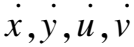
1.3 压缩感知

压缩感知作为一种新型的采样技术,能够以远低于奈奎斯特采样定理要求的频率进行信号采样.在拥有较少采样数据的情况下,压缩感知有很大概率恢复原始信号并且保证信号的准确性.

假设一个维离散信号为x=[x1,x2,…,xN]T,x∈Rn,存在正交矩阵Ψ∈Rn×n,使得:

x=Ψs

(2)

其中稀疏系数s=[s1,s2,…,sN]T,s∈Rn,Ψ表示稀疏矩阵,s是信号经过稀疏化表示后的稀疏向量.

需要构建一个与Ψ不相关的观测矩阵Φ去采样信号x,通过矩阵运算,得到低维的观测向量y=[y1,y2,…,yM]T,它包含原始信号的所有信息.采样过程为:

y=Φx=ΦΨs=Θs

(3)

其中Θ=ΦΨ称为感知矩阵,Φ是M×N的测量矩阵,Ψ是正交矩阵,s是稀疏系数矩阵.

信号可以使用压缩感知技术的两个必要条件分别是信 号的稀疏性和不相关性.但是,通常信号在变换域上不会呈现完全的稀疏性,而是部分稀疏,这样的信号也可以被认为是可压缩的.因此采用合理的信号稀疏表示方式对于信号的压缩和重构起着重要的作用.本文采用离散小波变换(DWT)对图像矩阵进行稀疏变换,其表示过程为:

x=WTsW

(4)

其中W是离散小波变换基矩阵并且满足WTW=I和WWT=I,s是信号的稀疏化表示.

本文采用随机矩阵生成测量矩阵,其中测量矩阵每一行都是通过向左移动前一行得到,初始行Φ是通过迭代混沌系统产生,测量矩阵为M×N矩阵.测量矩阵的第一行被设定为Φ(j-1,N),目的是为了减少列向量间的相关性,测量矩阵的生成过程为:

(5)

其中2≤j≤M,λ≥1.从测量矩阵的生成过程可以知道,它较容易生成,但是如果需要传输和存储大型的测量矩阵,会占很大的存储空间,本文提出的半张量积运算刚好可以避免这个问题.为根据恢复,需要解决一个最优化问题:

(6)

1.4 半张量积压缩感知

半张量积能够实现前一个矩阵的列数和后一个矩阵的行数不相同的矩阵运算,半张量积定义为:

(7)

其中X是一个行向量,且X∈Rnp,Y是一个列向量,且Y∈Rp,把X平均分成p块,每块大小为1×n.那么推广至矩阵,假设矩阵A∈Rm×n,B∈Rp×q,若是n是p的因子或p是n的因子,则A和B的半张量积T为:

(8)

半张量积压缩感知模型的定义为:

(9)

当t=1,半张量积压缩感知模型退化为传统的压缩感知模型,即:

yM×1=ΦM×N∝ΨN×N∝SN×1

(10)

当t>1时,测量矩阵Φ所需要的存储空间将成倍减少.

2 云存储中的压缩感知和生命游戏图像加密算法

2.1 生成忆阻混沌系统的参数

给定忆阻混沌系统的特征参数初始值,特征参数s,I,I1和I2的计算过程为:

(11)

(12)

(13)

(14)

其中P(i,j)是大小为m×n的图像矩阵P位于(i,j)的像素.对于256灰度图像,L=8,「x⎤表示最接近x的整数.

生成五维忆阻系统的参数,x1(0)、x2(0)、x3(0)、x4(0)、x5(0),具体生成过程为:

(15)

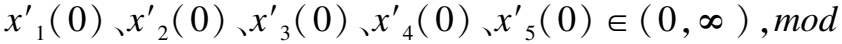
2.2 基于明文相关的生命博弈置乱方法

该方法简称PDGSM,主用于置乱明文图像的稀疏系数矩阵,从而降低矩阵向量元素间的相关性.利用GOL规则生成置乱矩阵SM,生成过程为:

(16)

其中Sn(i,j)是单元矩阵Sn位于(i,j)处的元素,n是迭代次数.为增加安全性,利用置乱矩阵SM置乱稀疏矩阵P1得到矩阵P2,其过程如图1所示.

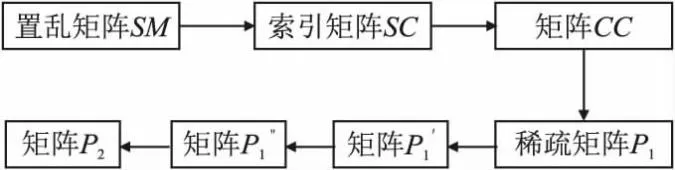
图1 矩阵置乱过程Fig.1 Scrambling matrix process

Step1.将置乱矩阵SM的每一行按照升序排序,得到索引矩阵SC,然后结合矩阵行的位置,得到矩阵CC.

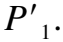
Step3.根据索引向量,对矩阵SM的每一列进行排序.

2.3 加密算法

通过对明文图像做DWT处理得到稀疏系数矩阵,然后通过基于明文相关的生命博弈置乱方法对该矩阵进行置乱、CS压缩、量化和密钥序列扩散,最后得到密文图像,加密算法过程如图2所示.

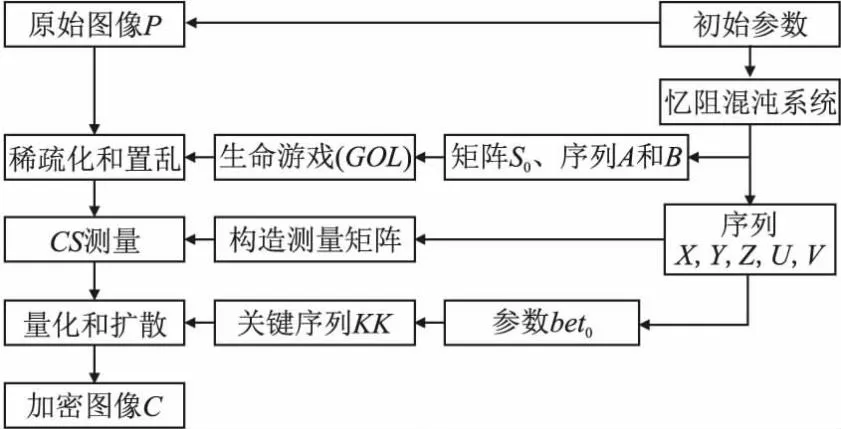
图2 加密算法过程Fig.2 Encryption algorithm process

具体加密步骤如下:

Step1.矩阵稀疏化.将大小为m×n的明文图像矩阵在DWT域中表示,得到稀疏系数矩阵P1,具体过程为:

P1=DWT(P)

(17)

Step2.混沌序列的生成.忆阻混沌系统迭代并生成混沌序列,需要迭代(N0+mn)次.X,Y,Z,U,V都是大小为1×mn的序列,且:

(18)

其中s是明文图像P的信息熵,最后得到5个混沌序列X,Y,Z,U,V,应用于PDGSM、压缩和扩散.

Step3.混沌序列的优化.通过重组5个混沌序列X,Y,Z,U,V,得到序列A和B,得到的序列A和B也是大小为1×mn的序列.A和B的优化过程为:

(19)

其中abs是计算数的绝对值,floor(x)是获取序列中不超过x的最大整数,并且5≤τ1,τ2≤16.A′和B′用于生成GOL的初始单元矩阵.

Step4.GOL初始细胞基质的生成.当S(j)=1,这是一个活细胞,当S(j)=0,这是一个死细胞,i=1,2,…,Mn.生成过程为:

(20)

把该序列调整为大小为m×n的矩阵S0.

Step5.置乱矩阵SM的生成.利用Step 4得到的矩阵S0,根据GOL规则进化n次,最后得到S1,S2,…,S，进而构造SM矩阵,具体过程为:

(21)

其中sn(i,j)指的是单位矩阵sn位于(i,j)的元素,n表示迭代次数,然后利用PDGSM对稀疏系数矩阵P1进行置乱,具体过程为:

P2=PDGSM(P1,SM)

(22)

Step 3～Step 5表示图像密码系统的排列过程.通过对Step 2生成的混沌序列进行重组和优化,在Step 3中生成另外两个随机序列A0和B0,它们在Step 4中用于生成GOL的初始单元矩阵S0.在Step 5中,通过GOL规则迭代S0得到置乱矩阵SM.矩阵SM具有随机性,即明文图像的元素可以移动到任意的位置,极大地提高排列水平.

Step6.结合半张量积和压缩感知技术测量矩阵P2.利用半张量积,根据两个已知大小为2×2的矩阵,经过多次循环操作生成一个高维矩阵,将其作用于由式(5)得到的矩阵,得到大小为M×N的测量矩阵Φ,且M=CR×m,N=n.将Φ作用于P2,得到大小为M×n的矩阵P2.

Step7.矩阵P2的量化.将矩阵P2的所有元素都量化成0～255之间的整数,量化过程为:

(23)

其中P3i和P4i是矩阵P3和矩阵P4第i个位置的元素,i=1,2,…,Mn,max和min是矩阵P3中的最大值和最小值.

在Step 6中,采用压缩感知技术,明文图像被压缩和加密,图像的体积减小.但是压缩后的图像,信息熵和随机性相应地也会降低.在Step 7中将压缩矩阵量化成图像矩阵,提高数据的安全性.

Step8.参数bet0的计算.利用明文图像的特征信息计算参数bet0,τ2∈[5,16],计算过程为:

(24)

bet0=mod(floor(bet×10τ3,5)+1

(25)

Step9.序列W的生成.从序列X,Y,Z,U,V中选择一个序列,记为W.当bet0=0时,则W=X;当bet0=1时,则W=Y;当bet0=2时,则W=Z;当bet0=3时,则W=U;当bet0=4时,则W=V.

Step10.扩散关键序列KK的获取.序列KK用来扩散明文图像,有利于数据隐私保护,其生成过程为:

KKi=floor((abs(Wi)-floor(Wi)×10τ4)mod256

(26)

其中τ4∈[5,16],Wi和KKi是序列W和KK序列的第i个位置的元素,i=1,2,…,Mn.

Step11.矩阵P4的扩散,迭代过程为:

(27)

其中SM1,1和SMm,n表示矩阵SM位于(1,1)和(m,n)的元素,s是图像的信息熵,P4i和KKi是矩阵P4和序列KK的第i个元素,⨁表示的是异或逻辑运算符,Ci-1是密码图像C的第(i-1)个元素,i=1,2,…,Mn.

通过Step 8～Step 11实现压缩图像的扩散.在Step 8中得到与明文图像有关的参数bet0;在Step 9中,利用bet0的值,根据序列X,Y,Z,U,V中得到序列W,在Step 10中,将W序列转换为范围为0～255的序列KK,在Step 11中,根据序列KK扩散图像P4.扩散过程可以改善压缩图像的随机性,增大其信息熵,从而能够抵抗熵攻击.

2.4 解密算法

图像解密是图像加密的逆过程,如图3所示.在解密之前,必须把解密参数发送给接收方,包括x′1(0)、x′2(0)、x′3(0)、x′4(0)、x′5(0)、s、I、I1、I2、min、max.

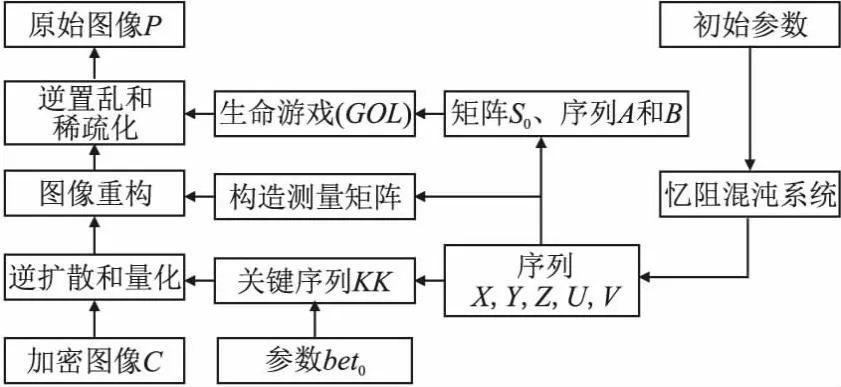
图3 解密算法过程Fig.3 Decryption algorithm process

具体解密步骤如下:

Step1.混沌序列的生成.首先使用解密密钥获得初始值x1(0)、x2(0)、x3(0)、x4(0)、x5(0),然后对忆阻混沌系统迭代得到5个大小为1×mn的混沌序列X,Y,Z,U,V.

Step2.初始单元矩阵和置乱矩阵SM的生成.生成过程和加密算法Step 3～Step 5的过程一致,先生成初始单元矩阵S0,再根据GOL规则把S0进化n次,得到S1,S2,…,Sn,进而得到SM矩阵.

Step3.逆扩散关键矩阵的获取.通过使用解密密钥I1,I2,利用等式获得密钥矩阵KK.

Step4.矩阵P4的生成.密文图像逆扩散,通过式(28)对大小为M×N的密文图像逆扩散,得到矩阵P4.

(28)

其中SM1,1和SMm,n表示矩阵SM位于(1,1)和(m,n)的元素,s是图像信息熵,P4i和KKi为矩阵P4和序列KK的第i个位置的元素,⨁表示异或逻辑运算符,CI-1是密码图像C的第(i-1)个位置的元素i=1,2,…,Mn,P4i是密钥.

Step5.矩阵P4的逆量化.利用密钥min和max对矩阵P4进行逆量化,具体过程为:

(29)

其中P3i和P4i是矩阵P3和矩阵P4的第i个位置的元素i=1,2,…,Mn,max和min是矩阵Pa中的最大值和最小值.

Step6.矩阵P2的重构.先获得测量矩阵Φ,然后根据OMP方法和矩阵P3重构出矩阵P2.

Step7.矩阵P1的生成,具体过程为:

P1=IPDGSM(P2,SM)

(30)

Step8.通过对矩阵P1的逆DWT操作,得到最后还原的明文图像,至此解密过程结束.

3 仿真结果和安全性分析

3.1 加密和解密结果

本文选择大小为512×512的医学图像和图像Lena作为测试图像,如图4(a)、(b)所示,其中算法单元矩阵的置乱度固定为18.本文分别将压缩比设置为0.25,0.5,0.7,它们所对应的密文图像和解密图像如图5和图6所示.图5中(a)-(c)表示医学图像不同压缩比所对应的密文图像,(d)-(f)是对密文图像进行解密处理后的重构图像.图6中(a)-(c)为 Lena图像不同压缩比所对应的密文图像,(d)-(f)是对密文图像进行解密处理后的重构图像.

图4 明文图像Fig.4 Plain image

图5 关于图4(a)的密文图像和解密图像(不同压缩率)Fig.5 Ciphertext image and decryption image of fig.4(a)(different compression rates)

图6 关于图4(b)的密文图像和解密图像(不同压缩率)Fig.6 Ciphertext image and decryption image of fig.4(b)(different compression rate)

观察上述明文图像、密文图像和解密图像,可以明显发现压缩比和密文图像的体积成正相关,和图像的重构效果成正相关.压缩比越大,则密文图像的体积越大,其重构效果越好;压缩比越小,则密文图像的体积越小,其重构效果相对较差.但是总体而言,该加密算法对于人像、医学图像的加密和解密都有不错的效果.除此之外,对明文图像加密获得的密文图像是不可被人眼识别的,并且在视觉效果上,重构后的图像依旧有着较好的辨识度.

为进一步验证加密算法的压缩和重建效果,本文使用峰值信噪比(PSNR)来定量地描述不同图像的区别,峰值信噪比公式为:

(31)

其中x(i,j)和y(i,j)分别表示明文图像和重建图像位于(i,j)处的像素值,N1×N2表示图像的大小.

当压缩比CR在0.25、0.3、0.4、0.5和0.7之间变化时,解密图像的PSNR值如表1所示,图像的峰值信噪比和压缩率总体呈正相关,随着压缩率变大,PSNR的值也会变大.表1中前3幅图像的大小为512×512,之后图像的大小均为256×256.总体来看,尺寸更小的图片PSNR值相对较低,当压缩率较低时,重构效果会差一些.相比于人像、动物、房子等图像,当压缩率相同时,医学图像的PSNR值更高,重构效果也更好.

表1 解密图像的PSNR值(不同压缩率)Table 1 PSNR value of decrypted image (Different compression ratio)

3.2 密钥敏感性分析

密钥敏感性是衡量密码系统是否有效的一个重要指标.针对两个参数x1、x2作了10-15的微小变化,只改变其中一个参数,其余参数均保持不变,其中压缩比为0.3,图像Lena和医学图像恢复效果分别如图7、图8所示.

图7 密钥敏感度分析Fig.7 Key sensitivity analysis

图8 密钥敏感度分析Fig.8 Key sensitivity analysis

观察图7、图8发现,即便参数仅仅发生很小的变化,明文图像也完全不能恢复,人眼观察是乱码,不能得到任何有效的信息.为更加客观的验证,本文采用均方误差(MSE)来量化参数的灵敏度,均方误差的定义为:

(32)

表2展示图像参数改变前后的均方误差,发现根据正确密钥恢复的图像MSE相对较小,即重建效果较好.观察被10-15干扰的密钥恢复的图像,均方误差很大,从中不能获取有效信息.因此,本文提出的加密方案对密钥高度敏感.

表2 正确和错误密钥恢复图像的MSETable 2 Correct and wrong key to restore MSE of image

3.3 图像熵分析

熵的概念源于热力学,图像熵广泛应用于图像加密处理领域,其直接反映图像所包含的有效信息量,其公式为:

(33)

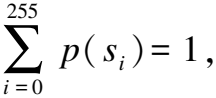
表3给出明文图像和密文图像的信息熵(CR=0.3).最后一行给出明文图像和密文图像的信息熵的平均值.根据图表结果,即便部分明文图像的信息熵只有6点多,大部分不超过7.5,密文图像的信息熵的平均值还是大于7.99,与8极其接近.因此,该加密方案能够很好地抵抗熵攻击.

表3 图像熵分析Table 3 Image entropy analysis

3.4 图像直方图分析

图像直方图可以很好的展示密文图像的恢复效果,若是最后恢复图像和明文图像的直方图尽可能接近,则密文图像的恢复效果较好.在图9中,明文图像如图9(a)、(b)所示,根据密文图像的恢复图像如图9(c)、(d)所示,其中图像(a)的大小为512×512,图像(b)的大小为256×256.在图10中,图9明文图像对应的直方图如图10(a)、(b)所示,根据密文图像的恢复图像的直方图如图10(c)、(d)所示.观察图9和图10,发现尺寸较大的明文图像和重构图像的直方图很接近,图像的重构效果较好,尺寸较小的明文图像和重构图像的直方图存在一定差距,图像的重构效果相对差一些.

图9 明文图像和解密图像Fig.9 Plain image and decryption image

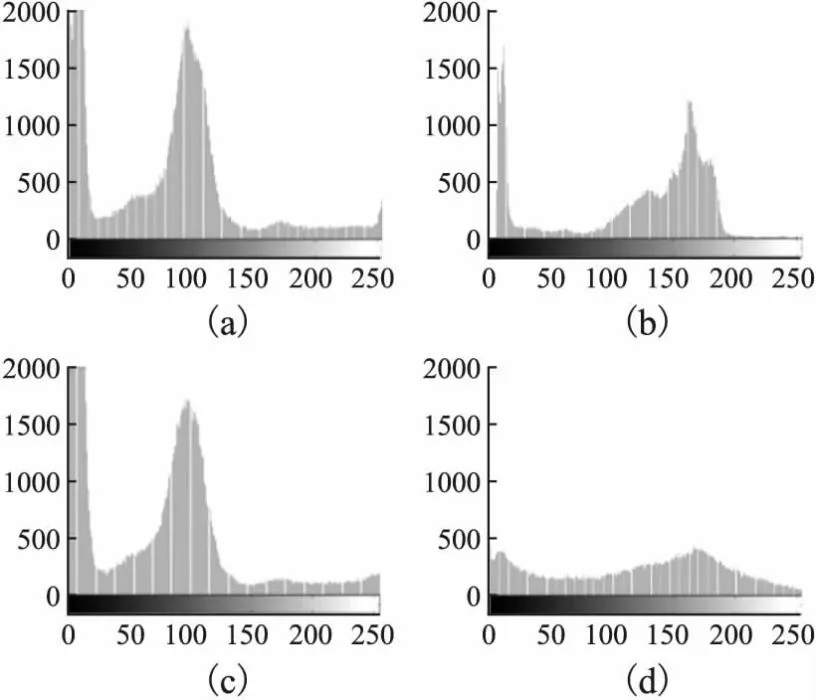
图10 图9明文图像和解密图像的直方图Fig.10 Histogram of plain image and decryption image in fig.9

3.5 图像像素相关性分析

本文通过计算图像相邻像素间的相关性来评判该加密方案的置乱效果.从明文图像中随机选取2000个相邻像素点,分别计算在水平、垂直和正对角方向上的相关系数.图11中(a)～(c)和(d)～(f)分别表示像素在水平、垂直和正对角方向上的明文图像Lena与其密文图像的相关性.可以发现明文图像相邻像素之间的相关性很强,与之相反,密文图像的相邻像素相关性明显降低,说明该加密方案具有很好的置乱效果.

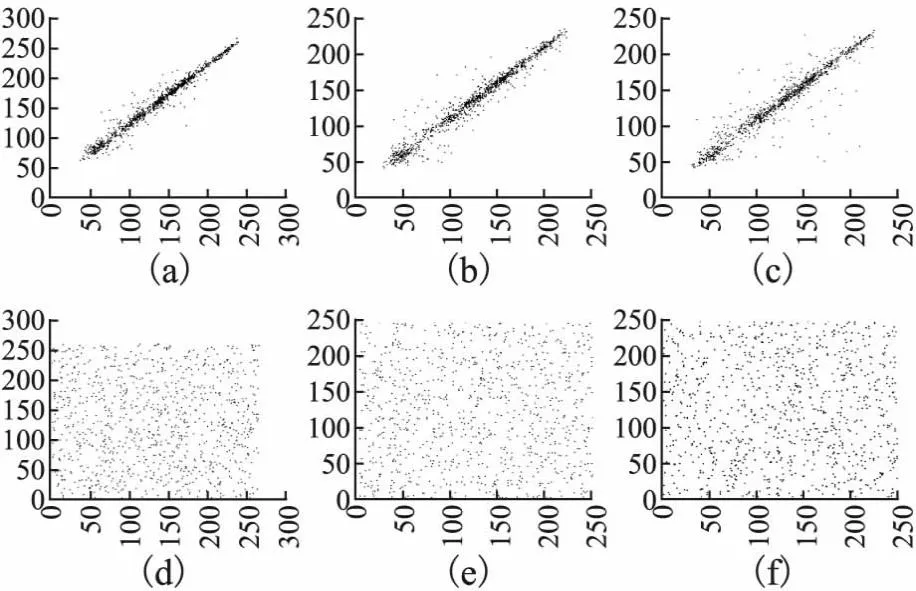
图11 相关性分析:(a)～(c)明文水平、竖直和正对角相关性;(d)～(f)对应密文相关性Fig.11 Correlation analysis:(a)～(c)plaintext horizontal,vertical and positive diagonal correlation;(d)～(f)corresponding ciphertext correlation

为更好地量化该方案的加密效果,本文引入相关系数,计算公式为:

(34)

表4 相关性分析Table 4 Correlation analysis

3.6 密钥空间分析

一般来说,密钥空间越大,攻击者通过搜索密钥来攻击图像加密算法的难度就越大.因此,一个有效的密码系统应当具备足够大的密钥空间,能够抵抗暴力攻击.该算法密钥包括参数x′1(0)、x′2(0)、x′3(0)、x′4(0)、x′5(0)和参数bet0等参数,拥有足够大的密钥空间,能够抵御蛮力攻击.

3.7 时间复杂度分析

假设明文图像的大小为m×n,Step 1主要消耗时间的步骤是将明文图像稀疏化,时间复杂度为Θ(m×n);Step 2的关键步骤是生成5个混沌序列的参数,时间复杂度为Θ(5×m×n);Step 3关键需要时间的是优化两个混沌序列,时间复杂度为Θ(2×m×n);Step 4的关键是比较得到的两个混沌序列,时间复杂度为Θ(m×n);Step 5的关键步骤是根据GOL规则得到大小m×n的置乱矩阵,时间复杂度为Θ(m×n);Step 6主要耗时间的是生成大小m×n的测量矩阵Φ,时间复杂度为Θ(m×n);Step 7用于量化CS后的测量值,时间复杂度为Θ(CR×m×n);Step 8～Step 9的时间复杂度为Θ(1);Step 10主要是生成密钥矩阵KK,时间复杂度为Θ(CR×m×n);Step 11主要是扩散大小为CR×m×n的序列,时间复杂度为Θ(CR×m×n);所以,本文提出的加密方案的时间复杂度为Θ(5×m×n).

4 结 论

本文针对云存储中隐私和能耗问题,提出一种结合半张量积—压缩感知和生命游戏技术的图像数据保护算法.该算法结合压缩感知和半张量积,节省图像数据在云存储传输过程中的空间,利用基于明文相关的生命博弈置乱方法,置乱稀疏图像,增强算法的安全性.此外,本文还采用混沌系统产生的混沌序列,结合生命游戏规则生成置乱矩阵,增强元素随机性,加强隐私保护.实验结果表明,本文所提出的图像数据保护算法具有密钥敏感性强、密钥空间大和图像重构效果较好等优点.

在提出的图像加密算法中,利用混沌系统所产生的序列来进行置乱和扩散操作,解密过程所耗费的时间增多,对图像实时传输不利.因此,在未来的研究工作中,如何提升算法的解密效率是值得研究的课题.