自行车是怎么保持平衡的?
差评君

在过去的一百多年时间里,自行车为什么不会倒这个问题,让无数物理学家、数学家想破了头。为此他们还发表过英、德、法、俄、意等各种语言的上百篇论文。法国科学院还为此设立了物理竞赛。而直到今天,这个问题也不能说是完全解决了。这样一个看似简单的问题,为什么困扰了无数科学家一个多世纪?
其实自行车早在18世纪就被法国人发明出来了,世界上第一辆自行车跟“自行”没有半毛钱关系。它没有驱动装置,没有脚踏板,甚至没有转向把手。看上去就是一个带两个轮子的长条板凳,得靠人来蹬地前进。由于实在太过原始,于是严谨的德国人给它加上了可控方向的车把。接下来几十年的时间,自行车的设计经过了欧洲多国的改进,期间外观甚至一度变成了非常反人类的造型。
到了1874年,终于它被英国人劳森改造成了正常人都能骑的样子。劳森发明了一种精密的机械结构——通过一条铁链让前轮在后轮的传动下运动,也就是我们现在熟悉的铰链。比马背还高的座椅也终于有机会从直径超过一米的前轮上移向更低更靠后的位置。可以说,“自行车”从一开始就不是依托缜密的物理学、数学理论公式设计而来,它的诞生完全根据生活经验。不过存在即合理,自行车不仅存在了近两个世纪之久,而且可以不借助人力自己保持平衡了,如此神奇的现象,肯定应该有个能解释它的科学依据吧? (以下讨论的稳定性都是“自稳定”,是指无人操作状态下自行车的稳定性。)
于是科学家们开始倒回去反推它的设计原理,结果发现:居然没法用现有的科学理论去解释自行车的平衡问题!1869年英国著名的力学家、工程师兰金发表了一篇题为《自行车运动的动力学原理》的文章,这也是最早讨论自行车平衡问题的论文。1899年,英国数学家惠普尔建立了一个由车体质量、车轮半径、转向角度等等25种复杂参数组成的模型,来研究不同参数对自行车平衡性的影响。1910年,在惠普尔的数据之上,德国物理学家索墨菲和数学家克莱因提出了“陀螺效应”——这个理论也被公认为是自行车保持平衡的奥秘。科普团队真理元素曾经做过实验,把几十斤重的铁饼,固定一端,在高速旋转的状态下,这个装置完全能战胜重力,给人一种不合常理的感受,就像有人拉着另外一端似的悬在半空。如果把它换成质量更轻的自行车车轮,那就更不在话下了。

因为车轮转动的方向是不变的,它的角动量方向也会一直指向側边,而当轮胎的旋转速度足够快的时候,不管车上有没有人操控,它们都会保持一个几乎恒定的方向前进,即使是出现倾斜,车体也不会随便改变方向,而是发生平移。这也是为什么,越是速度快的自行车,越是难以迅速转弯,因为你要施加足够大的力来对抗车轮的角动量。说到这,不知道“陀螺效应”这个理论能不能说服大家,而这套理论也主导了自行车研究界好长一段时间。
直到1970 年,有个叫琼斯的英国化学家突然跳出来说,自行车能够保持平衡,并不是因为“陀螺效应”而是另有原因!这人确实没瞎掰,他是真的发明出了抵消“陀螺效应”的自行车。这辆自行车的特别之处在于它有一大一小两个前轮!大前轮在小前轮的传动下,会向反方向旋转,也就是说这两个轮子的角动量是完全相反,且相互抵消的,所以这辆车成功地消除了“陀螺效应”!神奇的是,它也能和普通自行车一样保持平衡。一个近百年来公认的理论就这样被推翻了。
琼斯也给出了自己的理论解释。他认为,自行车之所以能保持平衡,是因为自行车的前轮设计里,有一个叫“前轮尾迹”的东西。简单说就是自行车前叉的延长线跟前轮中心垂直线的距离。懂汽车的朋友可能听说过一个词“主销后倾”,在原理上它和前轮尾迹是同一个东西。为什么这是自行车保持平衡的关键呢?当自行车行驶的时候,如果发生倾倒,车头会朝同一个方向转动,然后重心就会重新回到自行车前轮的下方,而出现这种情况,就是因为前轮中心比车把更靠前,重心会带着转向轴向一个方向转动。所以琼斯认为前轮尾迹越长,自行车的平衡能力也就越好。虽然他的理论听起来很有道理,但这就是自行车保持平衡的答案吗?


这辆自行车在没有“陀螺效应”并且“前轮尾迹”为负的情况下,依然能保持自平衡。
到了2011年5位学者在《科学》杂志上发表了一篇文章,他们论证了在既没有“陀螺效应”也没有“前轮尾迹”的条件下,自行车照样可以行驶得很稳定。他们做了一个更奇葩的自行车,先是在前后轮上加了反转的辅助轮,然后又让车轮中心在前叉之前。所以这辆车既没有“陀螺效应”,又是一个负的“前轮尾迹”,当然,它还是可以保持平衡稳定前进。那这辆车是如何保持平衡的?这辆自行车通过车身结构,来控制自身的质量分布。于是这5位学者给出结论:压根不用什么“陀螺效应”和“前轮尾迹”,只要在一定的质量分布的条件下,完全可以自平衡。
这篇论文并不是完全否定了前人的研究。相反,他们认为“陀螺效应”和“前轮尾迹”的理论非常重要,因为他们发现,其实自行车保持平衡的秘密早就被我们掌握了。还记得1899年英国数学家惠普尔建立的模型吗?这个模型由25个复杂参数组成,并涉及两个二阶微分方程。而这些方程的解表明,在受到微小扰动后,自行车的倾倒趋势会随时间而衰减,直至直立向前行驶。用大白话说就是,如果自行车要倾倒,就一定会发生转向,而有了这个转向就会使车子重新回正。所以他的研究就已经解释了自行车为啥不会倒。而“陀螺效应”和“前轮尾迹”理论其实是在解决为什么自行车倾倒后会发生转向的问题。
除此之外,有无数其他参数都可能会对稳定性造成影响。比如自旋动量,车把的倾斜,质心位置,前后组件的惯性等等。用5位作者的话说:自稳定的一个简单必要条件是——必须存在至少一个倾斜导致转向的因素。“陀螺效应”和“前轮尾迹”并没有错,他们都是自行车自稳定中的充分不必要条件。而这5位学者的研究为其增加了新的充分不必要条件,即车身质量分布。
所以,自行车保持平衡并不是一个所谓的“未解之谜”,只是在科学家们的研究下,这个问题经过了三次迭代,一次比一次完整,一次比一次理解深刻。现在已经有自动程序可以模拟自行车的平衡状况,大家可以通过调整不同参数来研究对自行车平衡性的影响。未来,说不定科学家们还会发现自行車保持平衡的新条件。
大家早已经可以轻松驾驭自行车了,你还在研究为啥自行车不会倒,岂不是没什么实用价值?法拉第用圆盘发电机来展示电磁感应原理时,一位观众问,“这东西有什么用呢?”而法拉第回答:“一个刚出生的婴儿有什么作用呢?” 正是有了这样的科学基础,无数后人才能将科学理论转化成现实世界的应用。这才是科学家们毕生努力的意义。
(责编:南名俊岳)
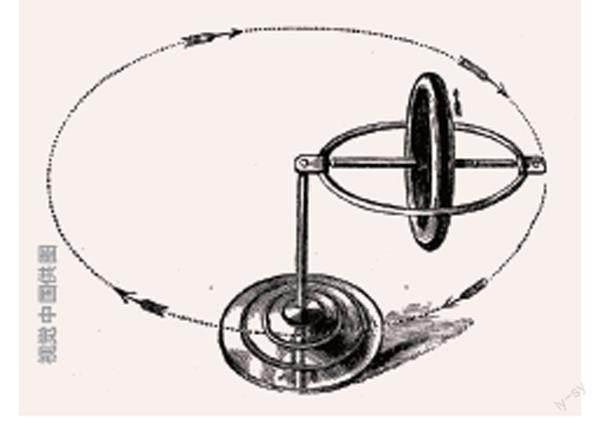
一是定轴性,二是进动性。拿大家小时候玩过的陀螺来说,旋转的陀螺,状态非常稳定,就算遇到外力干涉,它的平衡都很难被破坏掉。这是因为高速旋转的物体,会产生物理学上的“角动量”。力乘以力臂叫“力矩”,所以动量乘以动量臂就叫动量矩,也就是角动量。我们可以用“右手定则”来判断角动量的方向。此时陀螺的角动量方向就是垂直向上。而角动量的方向一旦形成,就极难改变,这就是“陀螺效应”的定轴性;陀螺除了“自转”以外,还会出现围绕垂直轴而形成的“公转”,这个状态就叫作陀螺进动。

