考虑需求侧响应的配电网柔性软开关优化控制方法

贾静然，段 昕，卢锦玲，李 丹，任 睿

（1.国网河北省电力有限公司电力科学研究院，石家庄 050000；2.华北电力大学电气与电子工程学院，保定 071003；3.河北省送变电有限公司，石家庄 050000）

近年来越来越多的有源配电网被广泛应用，通过应用有源配电网可发挥保护环境、节约能源、减少排放等功能[1]。随着我国风电、光伏等可再生能源的大规模并网发电，可再生能源的发电的随机性和波动性增加了配电网安全运行风险[2]。针对此类安全风险，主动配电网技术应运而生，该技术通过全新的调控方式使得配电网的操控更加灵活，可让配电网有效适应可再生能源发电的接入[3-5]，但是应用该技术容易使配电网系统的有功损耗电量增加，进而导致网损数值增加，渗透率较低，不能有效保障配电网系统的可靠运行。

柔性软开关作为一种全新调控方式，应用于配电网内可对无功功率进行补偿，对功率的流动方向、大小进行调控[6]。通过柔性软开关可降低配电网内可再生能源的出力误差，并对因接入高渗透率可再生能源而导致的电压越限等现象进行有效控制，有效保障分布式电源配电网的安全运行[7]。

当配电网接入各类分布式电源时，将增加其运行优化的繁琐性，而配电网需具备接纳各类分布式电源与实施有效需求侧管理的功能[8-9]。需求侧响应属于一种供需互动模式，即用户将激励机制或者电力市场价格信号作为目标对已有的电力消费方式进行优化改[10]。以往仅依赖发电侧对配电网系统的安全运行实时保障不具备经济优势，而在考虑需求侧响应的前提下，对用户的用电行为实施引导，令用户的用电行为更接近可再生能源的出力，此种方式可有效保障规模较大的分布式发电配电网系统的安全运行。

为了减少配电网系统的有功损耗电量，降低网损数值，提高新能源渗透率，我国早就开始进行相关研究，文献[11]中以智能软开关控制原理为基础，研究基于智能软开关SOP（soft open point）的供电联合优化模型，通过原始-对偶内点法求解，经实证验证，基于SOP 的供电联合优化模型方法的可行性，具有一定优化效果[11]；文献[12]中提出一种基于SOP 的交直流主动配电网优化控制策略，通过该方法在一定程度上降低配电网系统的有功损耗，解决节点越限等问题[12]。上述2 种方法可在一定程度上降低配电网的有功损耗，优化配电网的电路运行，但并不稳定，损耗并未降到最低。基于此，本文提出一种考虑需求侧响应的配电网柔性软开关优化控制方法，通过建立需求侧响应模型与柔性软开关优化控制模型，在考虑需求侧响应的前提下对柔性软开关进行优化控制，达到优化分布式配电网运行的目的，为配电网的安全经济运行提供有效保障。

1 考虑需求侧响应的配电网柔性软开关优化控制方法

1.1 需求侧响应模型的建立与求解

1.1.1 需求侧响应模型

所谓需求侧响应，就是用户根据实时的电价，结合相关政府机构的激励措施，主动对用电需求进行调整。

根据电力公司的响应程度，结合用户参与需求的侧响应过程，构建出以实现效益最大化为目标的需求侧响应模型。通过实现在各个时间段光伏发电曲线尽量接近对应的负荷需求，以此达到负荷转移的目标[13]，负荷转移的目标函数为

式中：PPV（t）和L（t）分别为t 时间段内的光伏发电功率与考虑需求侧响应之后的负荷电量；Lbefo（t）、LSLout（t）分别为t 时间段内考虑需求侧响应之前的负荷电量与转出的负荷电量；LSLin（t）为t 时间段内的转入负荷电量；T 为调度周期。

设第k 类负荷在t 时段初始运行时期的转入与转出单元数分别为ak（t）和bk（t），且0≤k≤MSL；第l 个工作时间段内第k 类平移负荷的功率为Plk；可平移负荷单元最高连续供电时间为gmax。那么，需求侧响应模型可表示为

式中：MSLc为一个调度时间段长的可平移负荷的类别量；MSL为可平移负荷的类别总量。

1.1.2 需求侧响应模型求解

将响应周期内的负荷与光照等数据输入后，获取用户预先设置的可平移负荷信息，确定可平移负荷的转入与转出时间段。经运算获得周期内各时间段的可转移负荷、光伏发电功率以及总负荷，若各时间段的总负荷均不小于光伏发电功率，那么此周期不实施负荷转移，直接进入到下一个周期内；反之，则将Pload＜PPV与Pload＞PPV两个时间段分别记为负荷转入和转出时间段。

确定转出时间段内可平移负荷单元总数与类别：运算出能转入的总电量与能转出的总负荷量LSin、LSout，取二者中最小值作为该周期内的负荷转移量，用nload表示。依据以上方式将转出时间段内能转移的负荷选出，并确定各转出时间段内可平移负荷的单元总数与类别。

利用粒子群算法求取不同转入时间段内所产生的负荷转入结果，通过nload与不同转入时间段内能转入负荷量共同确定原始区间，进而确定初始化粒子群，后将具备速度与任意位置的原始群P 生成，该原始群具备M 规模，其中位置由不同转入时间段的转入负荷单元总数与类别构成；通过统计不同粒子的适应值获取当前全局的最理想位置；对不同粒子的位置与速度进行更新；若没有满足最终条件则再次统计不同粒子的适应值以获取全局最佳位置，反之则将位置输出，完成负荷转入求解，输出负荷平移后曲线。需求侧响应模型求解过程如图1所示。

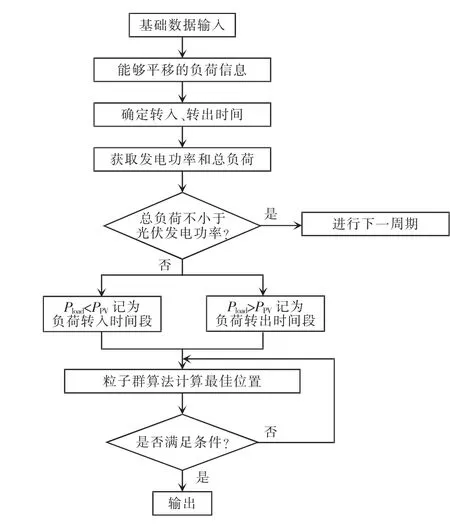
图1 需求侧响应模型求解过程Fig.1 Solving process of demand-side response model

1.2 配电网柔性软开关优化控制

1.2.1 柔性软开关模型

配电网柔性软开关的安装位置如图2 所示。

图2 配电网柔性软开关安装位置示意Fig.2 Schematic of installation position of flexible soft switch in distribution network

安装于2 条交流馈线之间的配电网柔性软开关，不仅可为配电网系统供应无功功率的补偿，而且还可实现对有功功率的有效调整，其优势在于优化控制配电网系统，令馈线之间可柔性互联，为负荷持续供电提供有效保障。

本文选取的配电网柔性软开关以背靠背电压源型变流器VSC 为基础，以PQ-VdcQ 为其控制模式，PQ-VdcQ 为一种混合控制方法，主要包括外环控制和整流控制，其运行变量主要由2 个VSC 所输出的无功与有功功率构成。由于少量VSC 装置在运行优化配电系统过程中的损耗同整个配电系统损耗相比微不足道，故本文不将柔性软开关的功率损耗考虑在内[14]。2 个VSC 所输出的无功功率需在符合各自容量约束的前提下保持互为独立的关系；而2 个VSC 所输出的有功功率之和应为0。柔性软开关的运行约束条件为

1.2.2 柔性软开关优化控制模型约束条件与优化

本文以现有研究为基础，研究配电网柔性软开关优化控制方法。在此阶段内的时间间隔设定为0.5 h，将目标函数设置为最低弃风弃光与配电网损耗，通过研究配电网未来1 周内可再生能源发电削减的有功功率及柔性软开关传输有功功率与无功功率的变化，实施优化控制。目标函数可表示为

式中：NR为可再生能源发电的数量；和分别为配电网系统在t 时间段内的网损与第n 个可再生能源有功出力规划数值；Δt 为时间间隔，且Δt=0.5 h；ηr和ηq分别为可再生能源的弃光弃风成本系数与配电网网络损耗成本系数；为第n 个可再生能源在t 时间段内的日前评估功率值。

本文通过设置约束条件来优化柔性软开关控制，其主要包括柔性软开关运行约束、可再生能源发电的出力约束、配电网辐射运行约束、配电网潮流约束及支路电流的约束等[15]。已知柔性软开关运行约束条件为式（3），配电网系统潮流约束条件可表示为

其中：

患有甲亢的孕妇TH分娩较为旺盛，会对腺垂体分泌促性腺激素产生一定的抑制效果，同时也会对三羧酸循环氧化磷酸化过程产生影响，能量消耗后就无法供给胎儿必要的营养，胎儿生长发育受限，分娩后，新生儿的体重也会较正常新生儿低[12-13]。

式中：φi为初始端节点为i 的支路尾端节点的集；θi为尾端节点为i 的支路初始端节点的集；Pt，ji和分别为在t 时间段内，由节点j 向节点i 流动的有功功率和无功功率；It，ji为电流幅值；Xji为支路ji的电抗；Rji为电阻；Pt，i和分别为在t 时间段内，总体流入节点i 的净有功功率总和与无功功率总和；和分别为由可再生能源发电输入到节点i 内的有功功率和无功功率；和分别为节点i 所负荷的有功功率和无功功率。

节点i 与节点j 在t 时段的电压幅值间的关系式为

式中，Ut，i，Ut，j分别为在时间段内节点i 和节点j 的电压幅值。

可再生能源发电的出力约束条件可表示为

节点电压的约束条件可表示为

式中：i∈D，D 表示全部节点的集合；Uimax和Uimin分别为节点i 的电压上下限值。

（4）支路电流的约束条件可表示为

通过以上约束条件的设定，完成对配电网柔性软开关控制的优化。

2 实验结果分析

选取Matlab 构建含柔性软开关的配电网系统架构仿真模型，应用本文方法对其中的柔性软开关实施优化控制，通过控制结果检验本文方法的性能。

2.1 负荷转移变化情况分析

检测在多云与晴朗两种不同天气场景下应用本文方法实施控制后，负荷曲线的变化情况，以此分析经本文方法控制后实验配电网系统的负荷转移变化情况，如图3 所示。

图3 不同场景下负荷转移变化情况Fig.3 Changes in load transfer under different scenarios

由图3 可以看出，在2 种不同天气场景下，经本文方法控制后缩小了负荷同光伏发电功率间的差距。无论是多云天气还是晴朗天气，光伏发电功率在06∶00—09∶00 不断增长，截至09∶00，其发电负荷就可达到2.1 MW·h，与控制后负荷、初始负荷持平。如是多云天气，在09∶00—15∶00 时段，会一直保持持平的模式，差距较小；15∶00 以后，光伏发电功率会逐渐下降至初始状态。如是晴朗天气，在09∶00—15∶00 时段，光伏发电功率会高于超越初始负荷与控制后负荷，与其仍有一段差距。综上，在多云天气场景下，经本文方法控制后，负荷同光伏发电功率间的差距最小；而在晴朗天气场景下，初始负荷、控制后负荷与光伏发电功率间的差距仍然较大，其主要原因是晴朗天气下光照充足，虽通过本文方法控制后负荷已由其他时间段向正午时间段转移，但因正午时间段的光伏发电功率过于突出，导致光伏发电功率仍旧比本文方法控制后负荷高出许多。综上可见，本文方法控制后可实现配电网系统的负荷转移，转移情况为由其余时间段向正午时间段转移负荷，对于负荷特性的改善及光伏发电特性的响应起到一定的促进作用。

2.2 电量损耗与消减情况分析

应用本文方法对配电网系统柔性软开关实施优化控制，对比优化前后不同时间段有功损耗电量、全天有功损耗电量以及可再生能源发电的全天削减电量情况，通过对比结果分析本文方法的控制效果，对比结果如表1 所示。

表1 实验配电网系统电量损耗及削减情况对比Tab.1 Comparison of power loss and curtailment in experimental distribution network system

由表1 可见，应用本文方法后实验配电网系统在不同时间段的有功损耗电量及全天有功损耗电量均明显低于应用本文方法前，其中全天有功损耗电量较应用本文方法前下降了41.37%；另外，应用本文方法后可再生能源发电的全天削减电量可降为0，无需对可再生能源发电的出力实施削减，原因是应用本文方法前配电网系统无法将电压越限完全消除掉，故而需对可再生能源发电的出力实施削减。而应用本文方法对配电网系统的柔性软开关实施优化控制后，能有效恢复电压在正常区间，故而无需对可再生能源发电的出力实施削减。由此可见，应用本文方法可明显改善配电网系统的有功损耗电量现象，并将配电网系统消纳可再生能源发电的性能显著提升，为配电网系统的经济运行奠定基础。

2.3 网损与渗透率情况分析

继续检验应用本文方法实施优化控制前后实验配电网系统的网损情况与渗透率情况，并运用所得检验结果进一步分析本文方法的控制效果。本文整个检验时间为20 h，从04∶00 开始测量，每4 h一组，共分为5 个时段，以04∶00—08∶00 为第1 时段，以08∶00—12∶00 为第2 时段，以12∶00—16∶00 为第3 时段，以16∶00—20∶00 为第4 时段，以20∶00—24∶00 为第5 时段，检验5 个时段中应用本文方法控制前后实验配电网系统的网损与渗透率情况，检验结果如图4 所示。

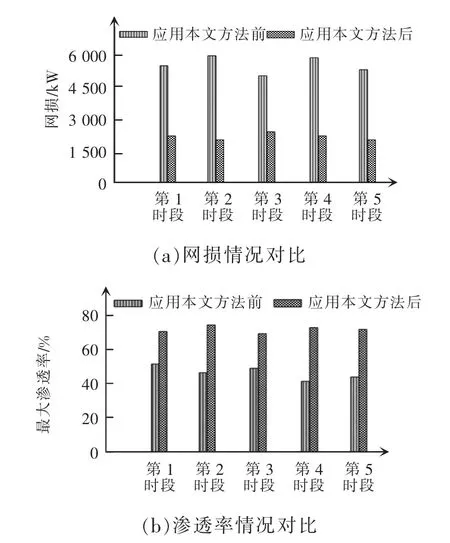
图4 实验配电网系统网损及渗透率对比Fig.4 Comparison of network loss and penetration rate of experimental distribution network system

分析图4 可知，应用本文方法后，实验配电网系统5 个时段的网损数值均远低于应用本文方法前，下降幅度均高于50%；应用本文方法前实验配电网系统最高渗透率为52.5%，应用本文方法后实验配电网系统的最高渗透率可达到74.6%，与应用前相比提升了22.1%，由此说明，应用本文方法不但可大幅降低配电网系统的整体网损量，同时还可显著提升配电网系统的渗透率，有效保障配电网系统的经济可靠运行。

3 结语

本文针对一种考虑需求侧响应的配电网柔性软开关优化控制方法展开研究，通过建立需求侧响应模型并实施求解，实现对配电网负荷的转移，在此前提下设计柔性软开关模型，并设定柔性软开关运行、配电网系统潮流、可再生能源发电出力及配电网辐射运行等约束条件，实现对配电网柔性软开关的优化控制。仿真实验验证结果表明，应用本文方法后，可由其余时间段向正午时间段转移配电网系统的负荷，有效改善负荷特性并响应光伏发电特性，降低配电网系统的有功损耗电量与整体网损量，提高配电网系统的可再生能源发电消纳性能及渗透率，达到对配电网系统运行优化的目的，保障配电网系统的经济安全运行。