上软下硬地层隧道盾构施工地表沉降影响因素及规律研究
袁侨蔚,刘远明,欧洵,黄城,李应肖
(1.贵州大学土木工程学院,贵阳 550025; 2.贵州省岩土力学与工程安全重点实验室,贵阳 550025)
引言
盾构隧道在上软下硬地层掘进时会对上部软土造成扰动,进而引起地表沉降[1]。贵阳地层中灰岩和白云岩分布广泛,部分岩层覆盖一定厚度的红黏土。与其他地区的软土不同,贵州红黏土具有高液限、遇水软化、失水强烈收缩、裂隙发育、易剥落的工程性质,构成了当地特有的上软下硬地层。但是,在这类地层中施工时,由于刀盘易结泥饼和受力不均,会面临推进阻力加大和盾构姿态及方向难以控制的问题[2],并且岩土交界面处红黏土的力学强度极低,易发生沉降超限、地表塌陷等现象[3],给工程安全带来了极大威胁。
此前,张会等[4]研究了掌子面内红黏土厚度对隧道地表沉降的影响;李炜明等[5]也提出上覆红黏土的厚度会直接影响地表沉降;何小辉等[6]分析了土层与岩层比例关系对盾构隧道洞壁变形的影响;范雨等[7]通过改变土岩交界面的位置研究了地层变形规律;郑世杰等[8]对双线隧道在不同软硬岩比例下的地表沉降进行了分析;田管凤等[9]引入地层复合指数来预测盾构隧道的地面沉降。可见,隧道开挖面处土层与岩层的厚度比例与地表沉降有着密切关系。此外,姚爱军[10]、贾宝新[11]、刘俊杰[12]、孙建[13]、宫亚峰[14]、聂耐[15]均利用土岩复合地层的地表沉降数据推导出了适用于当地的Peck修正公式。
由于盾构法首次在贵州上软下硬地层中使用,所以目前对贵阳地区盾构隧道穿越该地层的研究较少,另外贵州红黏土工程特性较复杂[16],因此,在当地开展不同土岩厚度比(开挖面内土层厚度与岩层厚度的比值)对双线盾构隧道地表沉降的影响很有必要,并在此基础上拟合出上软下硬地层的Peck分段公式,结果可为贵阳类似地层的地表沉降预测提供参考和借鉴。
1 工程概况
贵阳轨道交通3号线一期工程全长43.191 km,起点为花溪环城高速公路北侧的桐木岭站,终点为乌当区洛湾站,地铁全线多次穿越软硬不均的复合地层。
以桐木岭站-桃花寨站区间为研究对象,线路出桐木岭站后沿清溪路由南向北进入桃花寨站,地层表现为上覆可塑状红黏土层和下卧较破碎中风化白云岩层。区间设计起终点里程为右线YDK7+490.335~YDK8+639.479,隧道长1 149.144 m;左线ZDK7+490.335~ZDK8+639.476,隧道长1 149.616 m(其中长链0.475 m),埋深6~15 m。桐桃区间线路平面走向如图1所示,图2为断面DK7+510附近地质剖面。
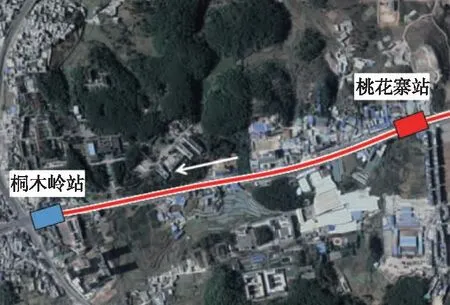
图1 桐桃区间线路平面Fig.1 Line plane between Tong and Tao
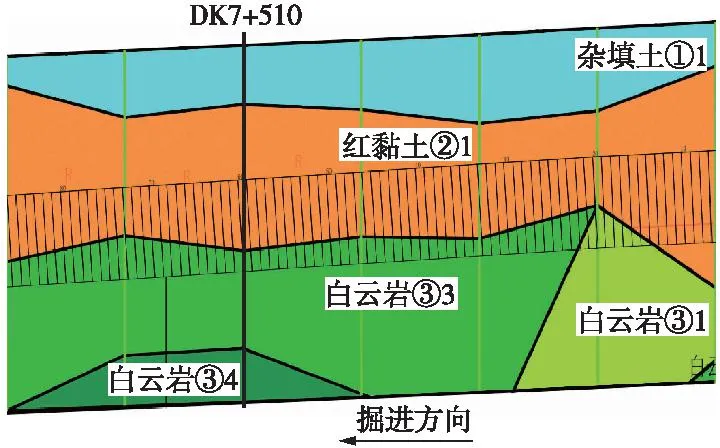
图2 断面DK7+510附近地质剖面Fig.2 Geological profile around section DK7+510
本工程采用盾构法施工,钢筋混凝土管片环宽1.5 m,共765环。内径5.5 m,外径6.2 m,厚0.35 m,强度等级C50,抗渗等级P12,管片组装方式采用“3+2+1”错缝拼装。
2 双线隧道盾构施工数值模拟
由于该区间红黏土层厚度不均,为研究不同土岩厚度比下双线盾构隧道的地表沉降规律,保持隧道埋深和双线隧道间距等条件不变,将开挖面分为7种工况:全断面红黏土层、土岩厚度比为3∶1、2∶1、1∶1、1∶2、1∶3、全断面中风化白云岩层,以此来模拟隧道穿越过程中的各种地层情况。不同工况和与之对应的断面如表1所示。

表1 不同工况与断面对应情况Tab.1 Correspondence between different working conditions and cross sections
2.1 数值模型建立
采用Midas GTS NX数值模拟软件,为减弱边界效应的影响,模型尺寸长80 m×宽60 m×高60 m。模型以自重应力为主,边界条件设置为四周和地面边界x、y轴方向位移均为零。
根据实际工程综合考虑,取双线隧道埋深12.3 m,双线隧道间距14.35 m,单洞内径5.5 m,外径6.2 m,管片厚0.35 m。基于区间隧道地勘报告,经过均匀化处理,将模型分为3层,分别为杂填土、红黏土和中风化白云岩层。三维模型中土层和注浆层(硬化前和硬化后)选用Mohr-Coulomb本构模型,盾构外壳和盾构管片选用弹性本构模型。地层物理力学参数和支护结构材料参数如表2、表3所示。
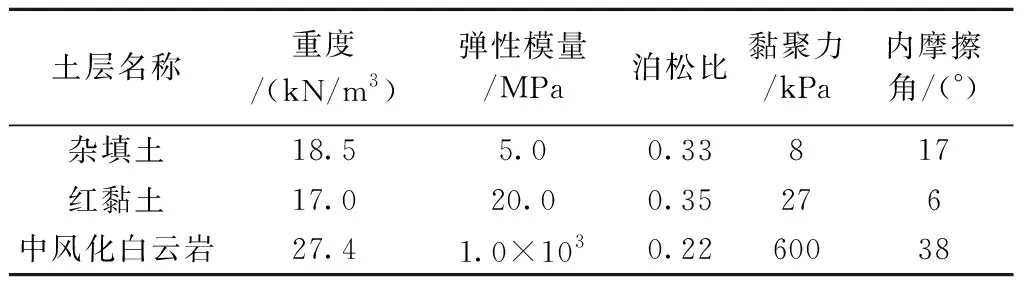
表2 地层物理力学参数Tab.2 Physical and mechanical parameters of the formation
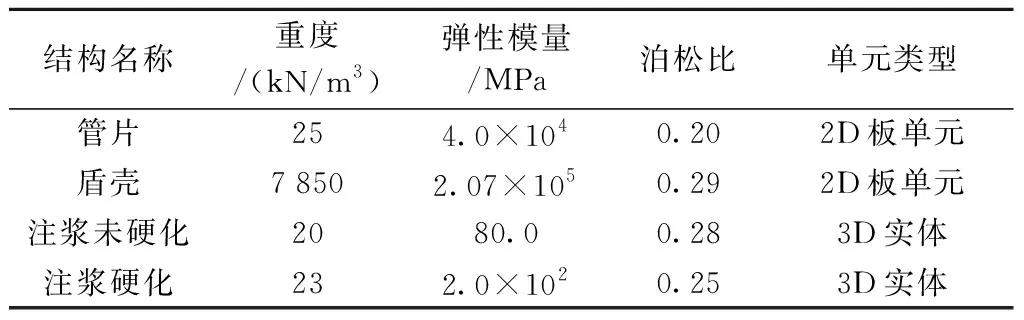
表3 支护结构材料参数Tab.3 Material parameters of the support structure
2.2 盾构施工模拟
不考虑地下水、盾构停机以及长期固结等影响因素,对双线隧道进行盾构开挖模拟,右线先行。开挖进尺为1.5 m,即一环管片的宽度,以两环管片作为一个开挖段(向前掘进3 m),每循环包含2个阶段:(1)钝化本开挖段内的全部土体,激活盾壳和掘进压力;(2)激活本开挖段的管片、注浆层、注浆压力和千斤顶力,并钝化掉盾壳。下个开挖段开始后,需要钝化上个开挖段的掘进压力、千斤顶力和注浆压力。其中,注浆层需要改变2次属性,首先是在浆液刚注入盾壳与管片之间时改变材料属性为液体弹性模量,接着将之前的注浆材料再次改变为浆液硬化后的材料属性。一个开挖段的完整施工过程如图3所示。
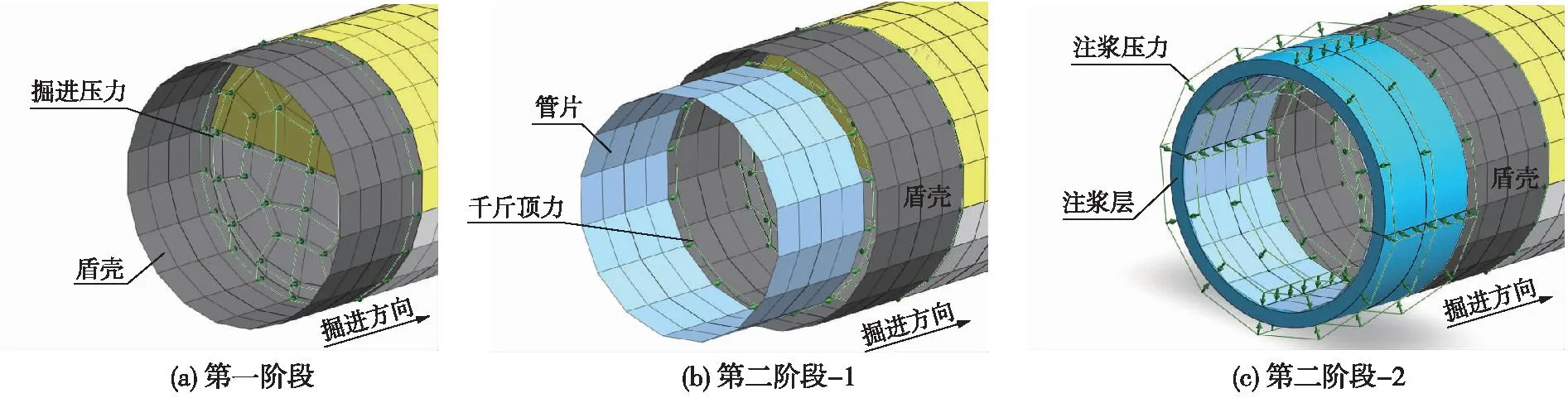
图3 一个开挖段的完整施工过程Fig.3 Complete construction of an excavated section
由于实际工程中左线间隔一个月后才出发,则施工阶段设置为右线全部开挖完成后,再进行左线开挖。最终建立的数值模型如图4所示,图4为土岩厚度比为1∶1时的计算模型。
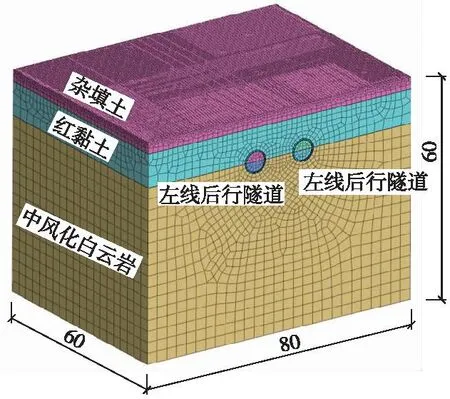
图4 三维数值计算模型Fig.4 A three-dimensional numerical computational model
3 实测值与模拟值统计分析
3.1 实测数据与模拟数据统计
为监测盾构掘进引起的地表位移,在隧道横截面上方地表每隔10 m设置一组沉降测点,每组测点布置如图5所示。
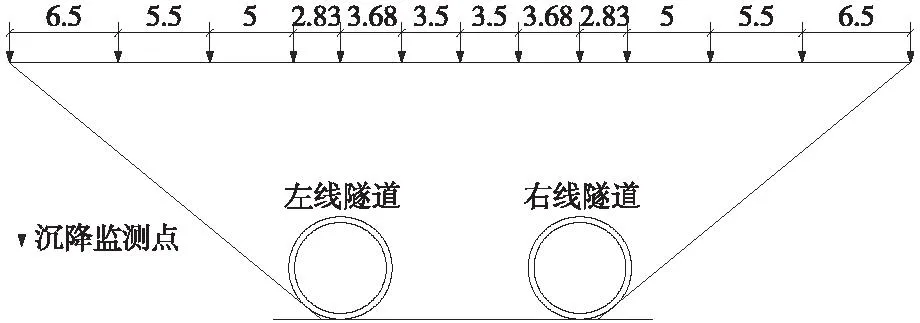
图5 地表沉降监测布置(单位:m)Fig.5 Surface settlement monitoring arrangement (unit: m)
在土岩厚度比不同的情况下,盾构隧道施工实际监测值与数值模拟沉降计算值对比如图6所示。

图6 不同厚度比下地表沉降的实测值与模拟值Fig.6 Measured and simulated surface settlement for different soil to rock thickness ratios
3.2 实测数据与模拟数据分析
对比分析图6不同土岩厚度比情况下,盾构施工引起的地表沉降值可以看出,部分工况的实测值与计算值还存在差异,但总体变化规律是相似的,说明数值模拟在一定程度上能够预测地表沉降的变形趋势。
整体来看,模拟计算出的地表沉降曲线大致呈W形,其“双峰”位于隧道左线和右线的中轴线处,地表最大沉降值均位于右线隧道轴心上方地表处。
如图6(a)所示,当隧道通过的地层只存在红黏土时,可以直观地看到实测值起伏不定,表现为不均匀沉降;数值模拟的沉降曲线有负值也有正值,地表隆起主要受到注浆压力和掘进推力的影响[17],而在软土地层中该扰动更显著[18]。实测曲线与模拟曲线都表现出明显沉降差,分别为18.45 mm和38.60 mm,即盾构隧道在单一软土中掘进时地表可能会出现较大变形,此外贵州地区红黏土的工程特性会加剧这种扰动。
以此为对照,在隧道埋深和双线隧道间距不变的情况下,随着开挖截面内岩层所占比例增大,实测曲线沉降规律性增强,沉降最大值逐渐出现在左、右线隧道附近;模拟曲线的形态从最开始 “左峰小右峰大”的陡峭型变为“左右双峰对称”的平缓型,对称性增强,沉降差值在缩小。表4对比了不同土岩厚度比下地表沉降的最大实测值和模拟值,两种数值大小基本对应且整体处于减小趋势,沉降值均小于规范控制值25 mm[19]。
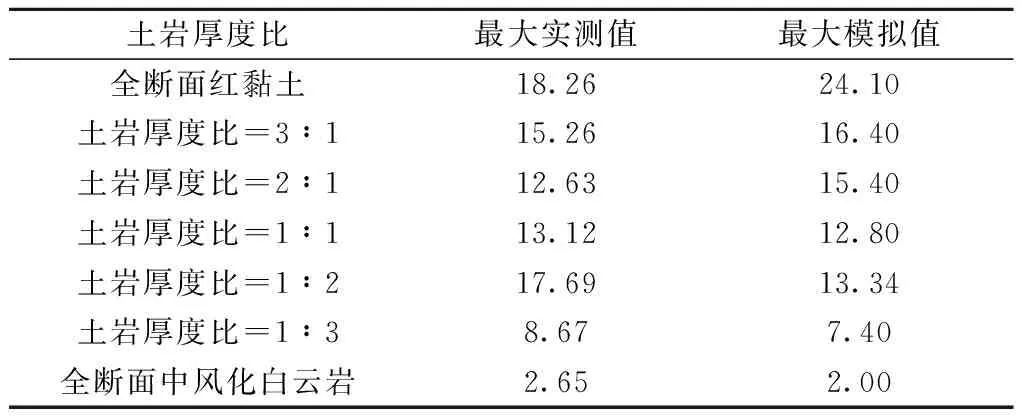
表4 不同土岩厚度比的地表沉降最大值 mmTab.4 Maximum surface settlement for different soil to rock thickness ratios
4 基于贵阳上软下硬地层的Peck修正公式
由3.2节提到部分实测沉降曲线与数值模拟曲线仍有差距,为能够更好地预测贵阳地区盾构隧道穿越上软下硬地层时的地表沉降,需要对Peck经典公式进行修正。
4.1 回归公式推导
单线隧道Peck经典公式[20]为
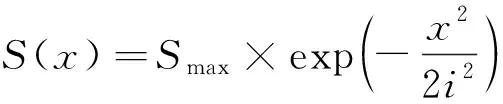
(1)

(2)
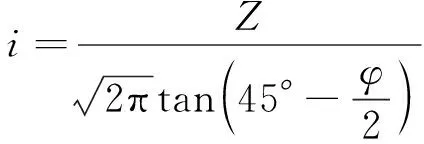
(3)
式中,S(x)为距离隧道轴线x处地表沉降量,m;Smax为地表最大沉降量,m;x为沉降监测点到隧道轴线的距离,m;i为沉降槽宽度,即沉降曲线反弯点的横坐标;Vi为盾构施工引起的隧道单位长度损失体积,m3;φ为周围地层的内摩擦角;Z为地表至隧道中心深度,m。
在等式两边取对数得

(4)
以lnS(x)和(-x2/2)作为回归变量,令lnS(x)为常数项,(-x2/2)为线性系数,进行回归分析
(5)
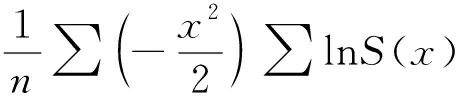
(6)
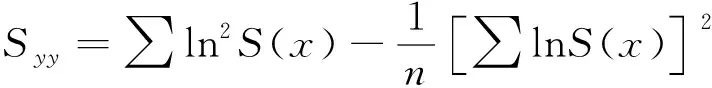
(7)
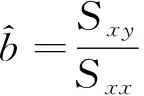
(8)

(9)
则回归方程变为

(10)
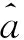
结合式(4)和式(10)可得
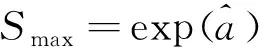
(11)
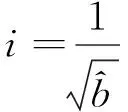
(12)
回归曲线为

(13)
采用线性相关系数检验回归函数的线性相关关系
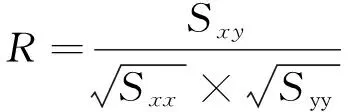
(14)
当R>r0.01(n-2)时,回归函数的线性关系高度显著;当r0.01(n-2)>R>r0.05(n-2)时,回归函数的线性关系显著。
4.2 实测数据回归分析
本区间为双线隧道盾构施工,右线先行,可利用双线隧道的地表沉降公式[21]
S(x)=S右+S左=
(15)
式中,Smax,r和Smax,l分别为右线和左线的地表最大沉降量;ir和il分别为右线和左线的沉降槽宽度;l为两条隧道的中心距离,且坐标原点取在两条隧道轴线中心位置。
双线隧道施工时的相互影响不可忽略,地表沉降也会互相叠加,现分别对该区段左右隧道的地表沉降实测数据进行回归分析。根据地表监测布置图,在进行单条隧道公式计算时,假定位于右线隧道轴心右边测点的沉降只受右线隧道施工的影响,位于左线隧道轴心左边测点的沉降只受到左线隧道施工的影响。
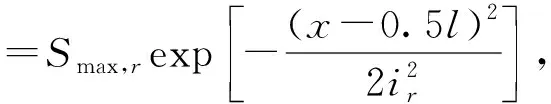

(16)
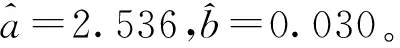
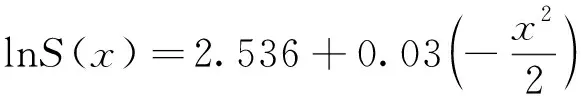
(17)
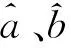
图7 右线回归拟合结果Fig.7 Regression fitting results for the right line

图8 右线拟合结果与实测数据对比Fig.8 Comparison of right line fitting results with measured data
(18)

图9 左线回归拟合结果Fig.9 Regression fitting results for the left line
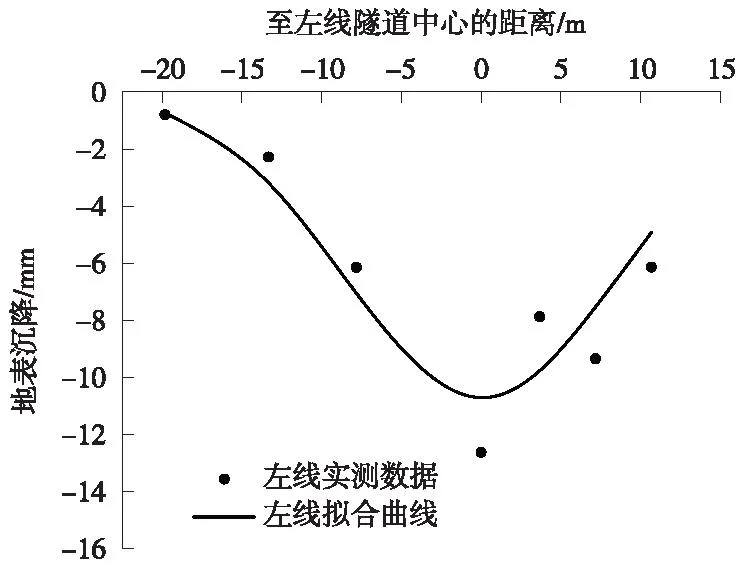
图10 左线拟合结果与实测数据对比Fig.10 Comparison of left line fitting results with measured data
4.3 双线隧道Peck公式修正
4.2节通过两组实测数据验证了经典Peck公式的适用性,现引入地表最大沉降修正系数α和沉降槽宽度修正系数β对公式进一步修正,则双线隧道地表沉降公式可改为
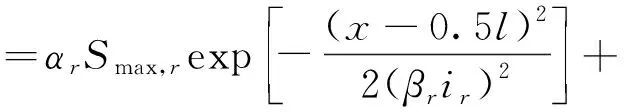
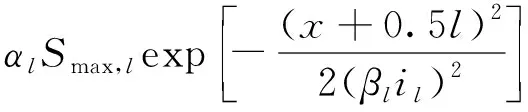
(19)
式(19)可拆分为左、右两个公式
(20)

(21)
将坐标原点分别定在左右隧道轴线处,并在等式两边取对数,可得到
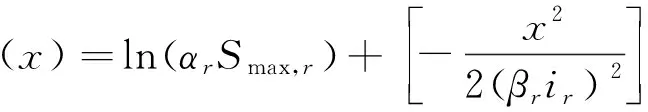
(22)
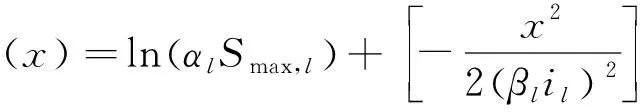
(23)
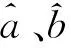
(24)
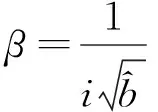
(25)
将该区间穿越上软下硬地层监测的44组地表沉降数据代入上述公式,并把左右线隧道算得的修正参数一起进行统计,得到α和β的概率分布图,如图11、图12所示。
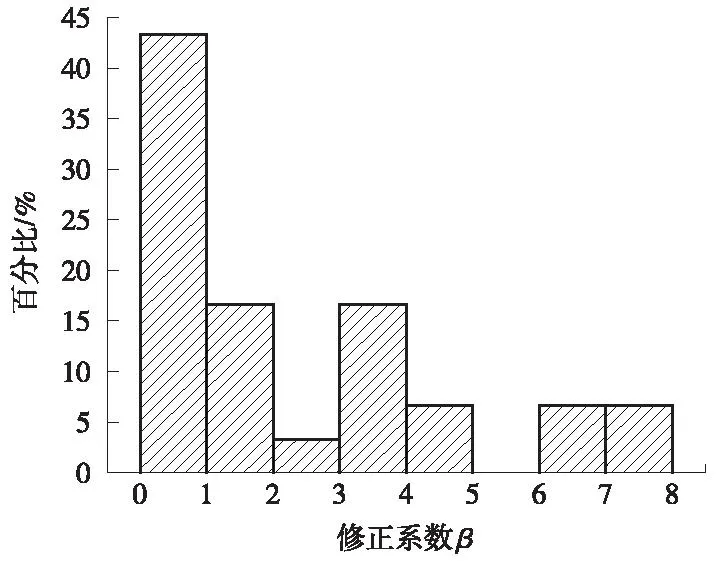
图12 修正系数β取值范围Fig.12 Range of values for the correction factor β
从图11、图12可看出,α主要分布在0~4,占80%;β主要分布在0.01~1,占87.18%。由此可以得出,地表最大沉降修正系数α取值在0~4,沉降槽宽度修正系数β取值在0.01~1。对修正系数取平均值:α=2,β=0.505,则上软下硬地层条件下双线盾构隧道的Peck修正公式为
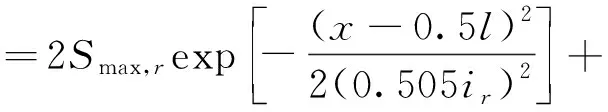
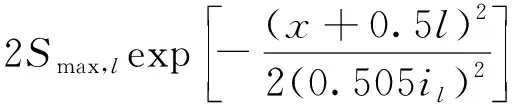
(26)
令α=0,β=0.01作为修正后的上限沉降曲线(由于α=0,曲线与x轴重合);令α=4,β=1作为修正后的下限沉降曲线。
任选一个断面将数据代入式(26)中,绘出Peck公式修正曲线、下限沉降曲线与实测沉降点的对比图,如图13所示。
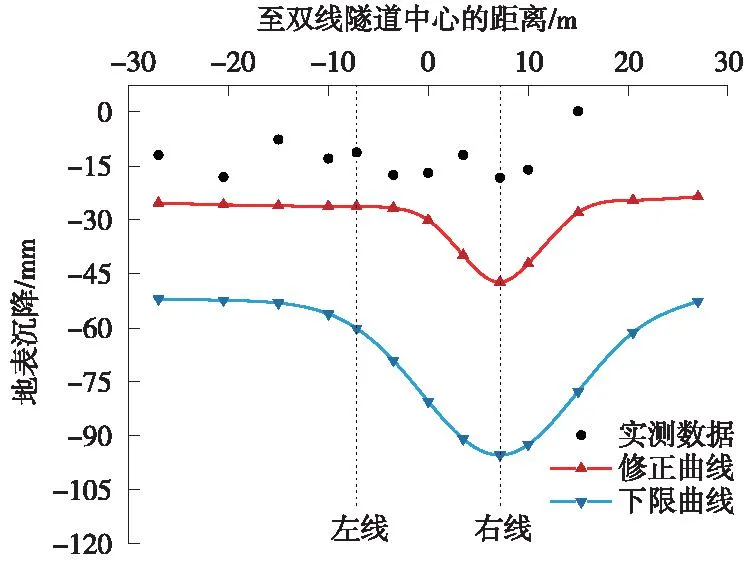
图13 断面DK7+530沉降曲线与实测值Fig.13 Settlement curve and measured value of section DK7+530
从图13可看出,修正后的沉降曲线和实测沉降点均在x轴与下限曲线之间,但修正曲线与实测沉降点仍存在差距。
由于拟合前假定的是左线隧道中心左侧沉降和右线隧道中心右侧沉降互相不受到另外一条隧道开挖的影响,只需叠加双线隧道中间区域地表的变形。则式(19)可改为分段函数形式

(27)
从α和β的取值范围内选择合适的修正系数组合代入式(27)中,画出不同土岩厚度比下的分段函数曲线,并与实测沉降值进行对比,如图14所示。
图14 不同土岩厚度比下的分段曲线与实测值Fig.14 Segmentation curves and measured values for different soil to rock thickness ratios
由图14可以看出,修正后Peck分段函数沉降曲线更加接近实际沉降值。最后按照各土岩厚度比对应的修正系数绘出关系图,如图15所示,修正系数α和β的分布都比较均匀,前者主要在1.35附近,后者主要在0.6附近。
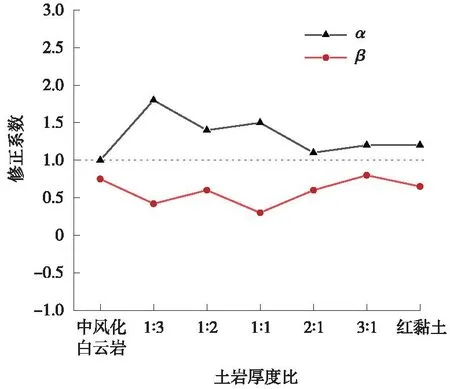
图15 土岩厚度比与修正系数关系Fig.15 Relationship between soil to rock thickness ratio and correction factor
5 结论
(1)在保持隧道埋深和双线隧道间距不变的情况下,数值模拟得出双线隧道盾构施工引起的地表沉降曲线均表现为W形,且地表最大沉降值都在右线隧道轴心的上方地表。
(2)以盾构隧道穿越全断面红黏土为参照,地表沉降在该种地层中更易受到扰动而发生较大变形,表现出不均匀沉降,并且红黏土的工程性质都会对地上和地下结构造成威胁。随着土岩厚度比减小,沉降曲线趋于平缓,对称性逐渐增强,整体沉降值变小。根据实测与模拟结果,沉降值均处于安全范围内,但建议隧道在穿越开挖面内红黏土比例较大的复合地层时,需要加强监测并做好防治措施。
(3)通过经典Peck公式对区间隧道的44组实测数据进行拟合计算,推导出了地表沉降分段函数公式,并得到地表最大沉降修正系数α和沉降槽宽度修正系数β的取值范围,分别为0~4和0.01~1。从取值范围中选择恰当的修正系数组合,结果表明,修正后的分段函数曲线更加趋近贵阳上软下硬地层的实际沉降,进一步得到土岩厚度比与修正系数的关系。

