密贴下穿既有地铁车站的新建通道拆撑影响分析

曹 攀，章慧健，杨宇杰，张 帅，郭宏博

(1.西南交通大学交通隧道工程教育部重点实验室,成都 610031; 2.西南交通大学土木工程学院,成都 610031;3.广州地铁设计研究院股份有限公司,广州 510010)

引言

随着城市轨道交通的快速发展,新建地铁隧道(车站)近接既有地铁隧道(车站)施工的情况越来越多[1-3]。为减小扰动影响,新建隧道施工往往采用化大为小、增加临时支撑的分部开挖方法[4-6]。尽管临时支撑在正常服役阶段可以通过减跨提高开挖安全性,但是拆除临时支撑会引起结构受力体系转换,因而确保拆撑风险可控对于整个工程的施工安全十分重要。国内外学者对于隧道拆撑也进行了大量研究,田海波[7]针对平顶直墙条件下浅埋暗挖通道开挖和二次衬砌施工风险,对平顶直墙结构断面适用条件进行分析,提出了不拆撑条件下的平顶直墙暗挖结构二次衬砌施工方法;朱正国等[8]以乌蒙山2号隧道为例,采用数值模拟方法对开挖过程进行计算,分析了开挖过程中围岩与支护结构的应力以及变形变化特征,为拆撑提供了理论依据。张俊儒等[9]通过数值模拟及现场实测方法对新考塘隧道拆撑时的初支内力及安全系数进行分析,得到了双层初期支护对于拆撑安全性的控制效果;柳献[10]等采用模型试验方法研究盾构主隧道在机械切削过程中的结构响应,得出拆撑步在整个施工中最危险,弯矩增量达到40～60 kN·m;张建国等[11]采用数值模拟及现场实测对厦门翔安隧道陆域CRD法施工进行了分析,得到纵向一次拆撑长度为10 m时对初支的影响较小;刘涛等[12-13]采用现场实测数据分析和数值模拟相结合的方法,对比拆撑前后围岩与初支变形情况,进而对6 m范围内交替拆撑,并以6 m为工作单元间隔拆撑的拆撑方案安全性进行分析,得出地表沉降、拱顶沉降及净空收敛在拆撑前后增长量及影响均较小,可知初支的安全性受支撑拆除的影响较小;孙克国等[14]以青岛地铁3号线某暗挖地铁站为例,采用理论分析、数值计算和现场监测3种手段,利用增量法对临时支撑拆除过程中围岩与结构的变形和内力变化规律进行研究,得出临时支撑拆除的影响范围为30 m,并结合车站周边环境的允许位移值,确定并验证了单次拆撑长度6 m时较为安全;雷震宇等[15-16]采用荷载-结构模型研究了南京地铁鼓楼站-玄武门站区间渡线隧道拆撑过程,采用增量法得到了拆撑过程中结构内力变化规律,确定了合理的拆撑方案;炊鹏飞[17]以北京地铁14号线东湖渠站工程为例,通过对临时支护的拆除时间、方式以及长度分析,得到了一套安全合理,操作简便的施工技术。

综上,以往研究成果主要是对单体隧道或地下结构拆撑风险分析,且多以对比不同拆撑长度带来的影响差异。依托成都地铁8号线倪家桥站新建换乘通道零距离密贴下穿既有1号线车站工程为背景,对比分析“先施作二衬再拆撑”和“先拆撑再施作二衬”两种施工顺序对既有和新建结构的力学差异,并基于“先拆撑再施作二衬”工况进一步分析拆撑方案,为类似工程施工提供指导。

1 工程概况

新建成都地铁8号线倪家桥车站换乘通道密贴下穿既有地铁1号线倪家桥站近接施工工程,两线在下穿段为正交关系,具体平面如图1(a)所示。暗挖段密贴既有车站底板,暗挖段结构宽23.4 m,高9.05 m,下穿段长17.3 m,暗挖段剖面如图1(b)、图1(c)所示。既有车站和新建通道的主要结构尺寸如表1所示。

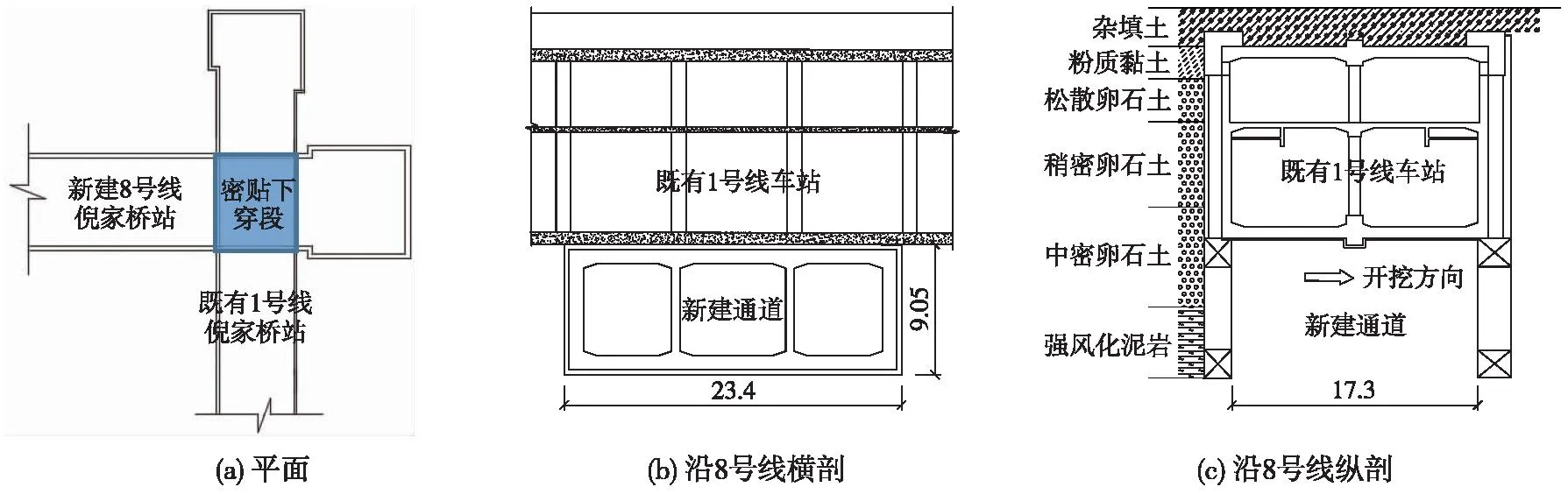
图1 新建通道与既有车站的相对位置关系(单位:m)Fig.1 The relative position relationship between the new underpass and the existing station(unit: m)

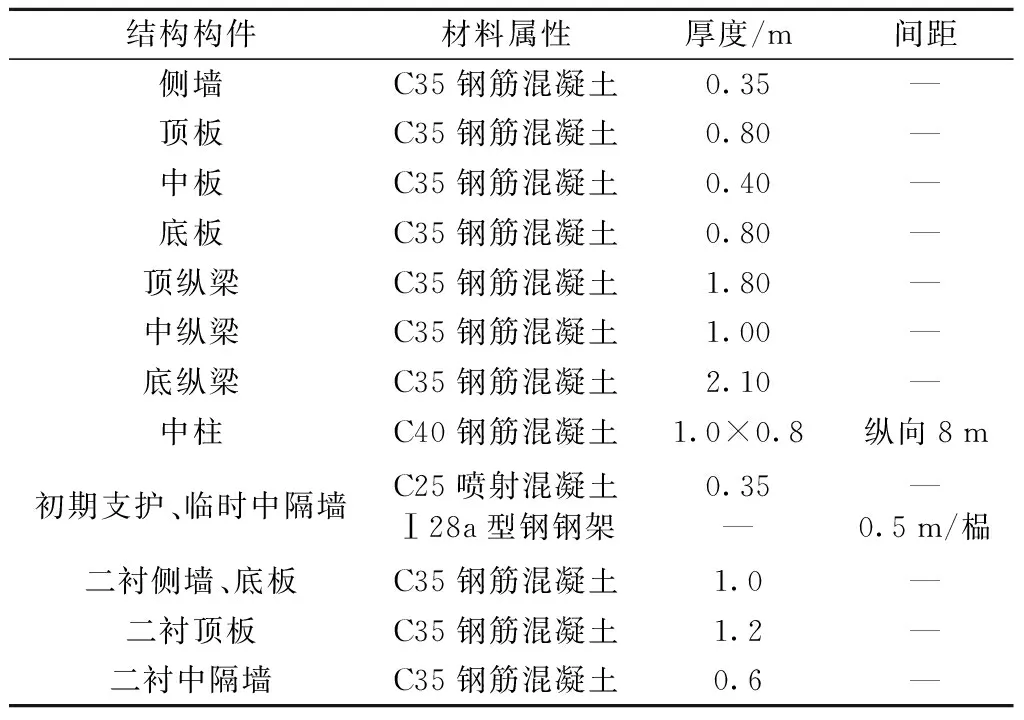
表1 既有地铁车站和新建通道的支护参数Tab.1 Lining parameters of the existing subway station and newly-built underpass

2 两种拆撑工况力学差异对比分析

2.1 计算模型与计算参数

运用FLAC3D对上述两种工况进行模拟研究,计算模型如图2所示,对模型前后左右边界施加水平约束,底面施加竖向约束,顶面为自由面;采用实体单元模拟围岩及支护结构,分别服从Mohr-Coulomb准则和弹性准则。土层厚度及物理力学参数如表2所示,支护结构计算参数如表3所示。

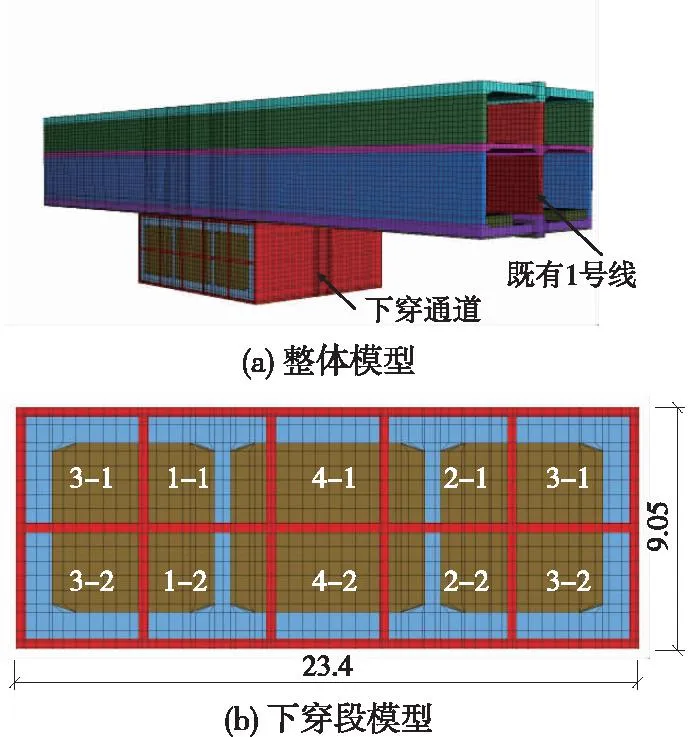
图2 计算模型(单位:m)Fig.2 Calculation model (unit: m)

表2 土层物理力学参数Tab.2 Physical and mechanical parameters of the soil layer

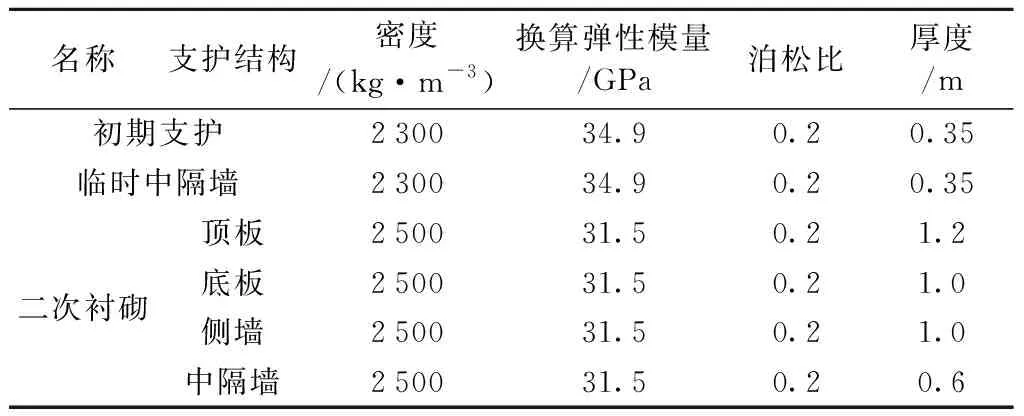
表3 支护结构计算参数Tab.3 Calculation parameters of the lining structure

需说明的是:初期支护中钢拱架作用按其弹性模量折算给喷混凝土考虑,具体计算方法见式(1)。

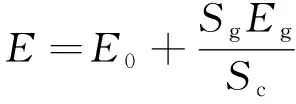
(1)

式中,E为折算后混凝土弹性模量;E0为原混凝土弹性模量;Sg为钢拱架截面积;Eg为钢材弹性模量;Sc为混凝土截面积。

2.2 施工过程数值模拟实现

计算采用分部开挖进行,具体分块如图3所示,分为两种工况,工况1(现场实际施工工序,拆撑长度为11 m)为“先施作二衬再拆撑”;工况2为“先拆撑再施作二衬”。各导洞开挖进尺均为2 m,此节中数值模拟中考虑最不利情况,即拆撑时一次性将新建通道纵向所有的临时支撑全部拆除,具体计算步骤如表4所示。

图3 导洞分块示意Fig.3 Schematic diagram of the pilot tunnels

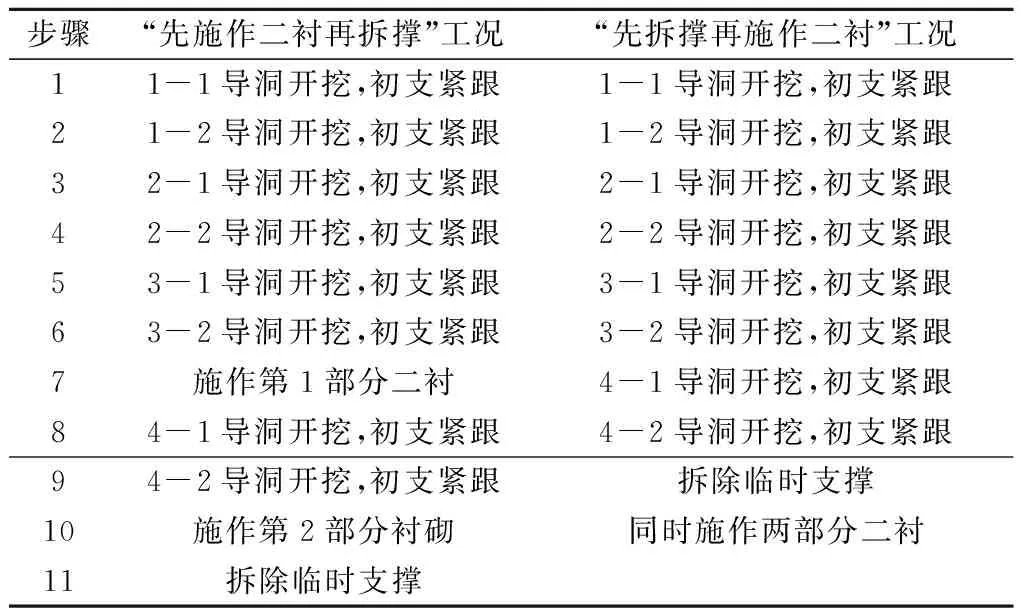
表4 新建通道分部开挖主要计算步骤Tab.4 Main calculation steps of the new underpass with partial excavation

2.3 计算结果分析

拆除临时支撑改变了结构受力体系,对新建通道初支结构和既有车站结构均会产生影响。以下分别从结构沉降、弯矩两方面来对比分析两种工况下的拆撑附加影响。

2.3.1 既有车站拆撑影响分析

提取两种工况拆撑前后位于下穿范围内的既有车站中部断面弯矩图,如图4所示。对于“先施作二衬再拆撑”工况,拆撑前后弯矩变化差异很小,拆撑后弯矩最大值为26.85 kN·m,位于车站顶板左边墙处(开挖进口端)。对于“先拆撑再施作二衬”工况,拆撑前后弯矩形态及大小改变较大,拆撑后弯矩最大值为41.18 kN·m,出现在底板跨中,拆撑后车站顶板、底板下侧受拉的范围增大,拆撑对于既有结构而言是一种下拽力作用。

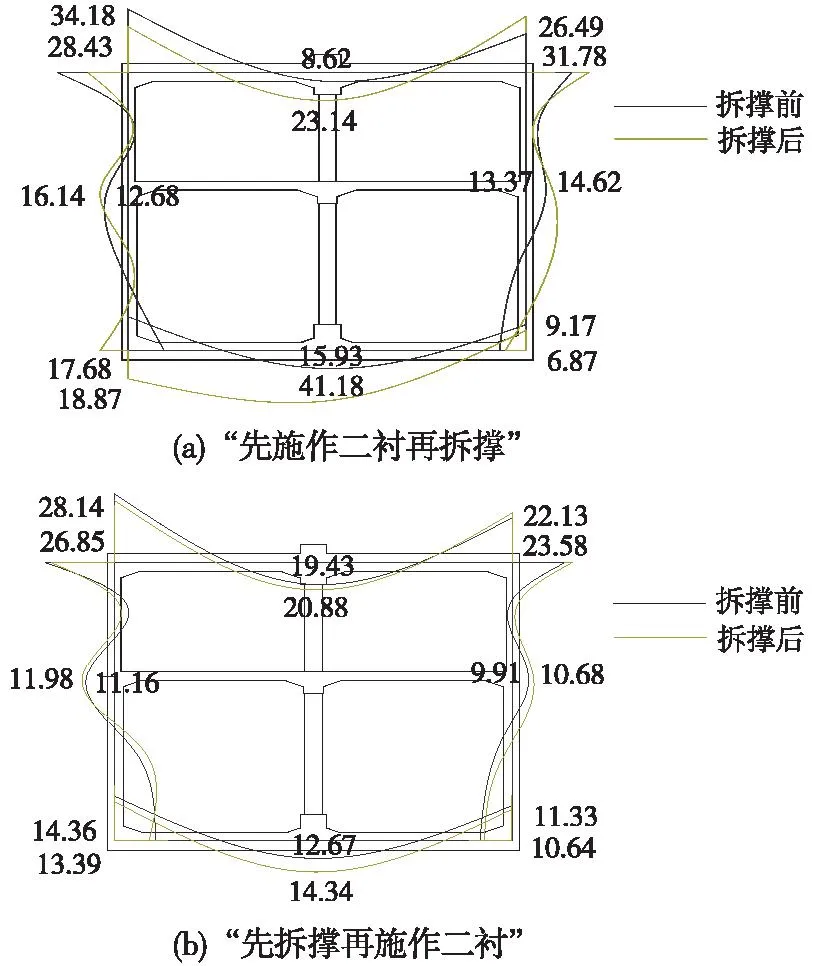
图4 既有车站结构拆撑前后弯矩对比(单位:kN·m)Fig.4 Comparison of the bending moments of the existing station structure before and after dismantling lining (unit: kN·m)

提取下穿通道纵向中部位置在两种工况拆撑前后既有车站的底板沉降做沉降槽曲线,如图5所示。可以看出:对于“先施作二衬再拆撑”工况,拆撑导致的沉降增量最大值为0.13 mm,底板两端沉降几乎相等,拆撑后沉降槽曲线形态几乎无差别,车站底板沉降最大值为4.41 mm,所以先施作二衬对既有车站底板沉降具有很好的控制作用;而对于“先拆撑再施作二衬”工况,拆撑后曲线呈现更明显的沉降槽特征,拆撑影响范围主要集中在下穿通道开挖边界对应的既有车站区域,沉降曲线形态由平底锅形向沉降槽变化,拆撑导致底板最大沉降增量及最大沉降量分别为4.86,8.87 mm,而底板两端整体沉降增加0.4 mm,影响较小。

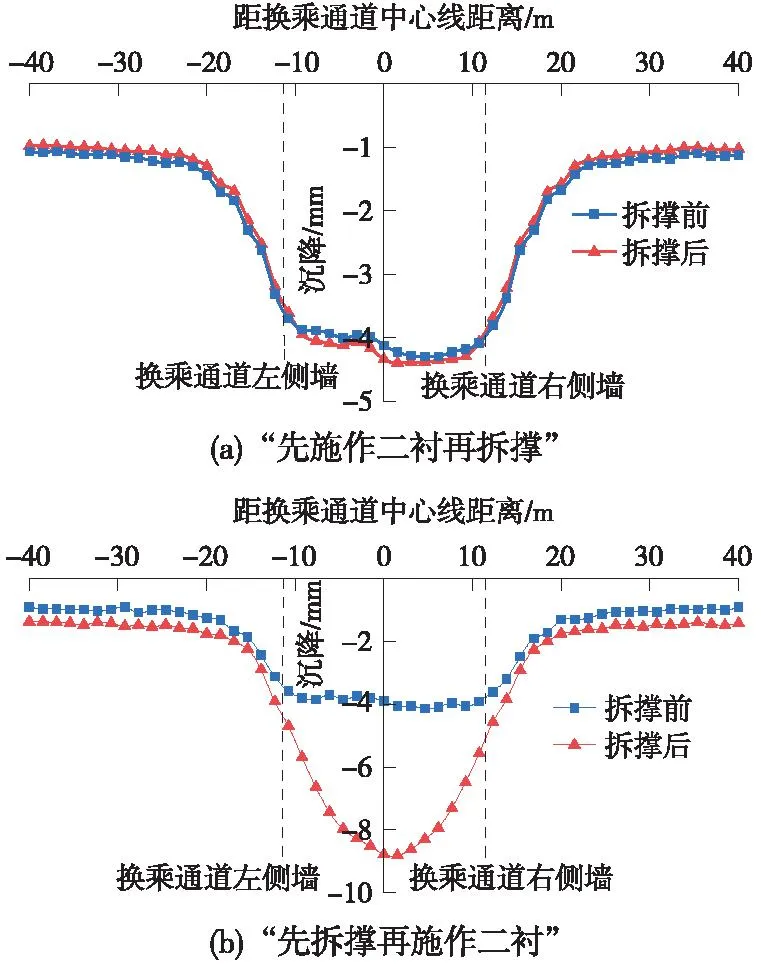
图5 既有车站底板沉降曲线Fig.5 Settlement curve of the floor of the existing station

2.3.2 新建通道支护结构拆撑影响分析

提取两种工况拆撑前后新建通道纵向中部断面初支、二衬弯矩值,具体如图6所示。可以看出:对于“先施作二衬再拆撑”工况,拆撑前后弯矩线近似重合,总体上底板上承受的弯矩较大,拆撑后初支弯矩最大值为32.41 kN·m,出现在 2-2导洞底板跨边位置;二衬弯矩最大值为12.65 kN·m,出现在左侧3-2导洞(临近左侧墙)底板跨边位置,拆撑对于结构受力变形的影响不明显。对于“先拆撑再施作二衬”工况,拆撑后初支受力状态多处发生改变,如顶板、底板基本处于内侧受拉状态,侧墙中部也是由外侧受拉变为内侧受拉,拆撑后初支弯矩最大值为46.20 kN·m,位于3-2导洞(临近左侧墙)底板跨边。

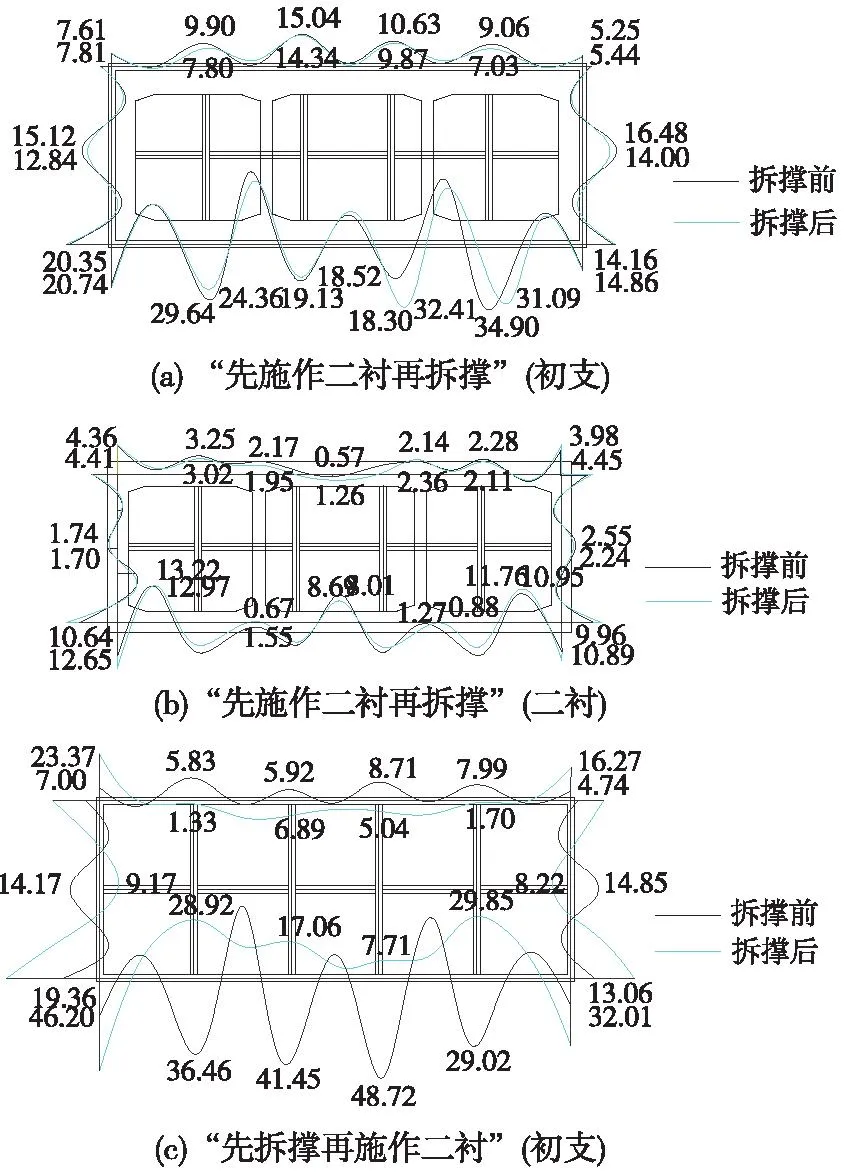
图6 支护结构拆撑前后弯矩对比(单位:kN·m)Fig.6 Comparison of the bending moment of the lining structure before and after dismantling lining (unit: kN·m)

图7为“先施作二衬再拆撑”工况下拆撑前后二衬结构的第三主应力云图,拆撑前二衬第三主应力最大值为0.12 MPa,二衬结构受力很小,而临时支撑最大第三主应力达到6.05 MPa。拆撑后二衬中隔墙第三主应力明显增加,可知竖向临时支撑的力主要由二衬中隔墙承担,二衬第三主应力最大值为2.67 MPa。

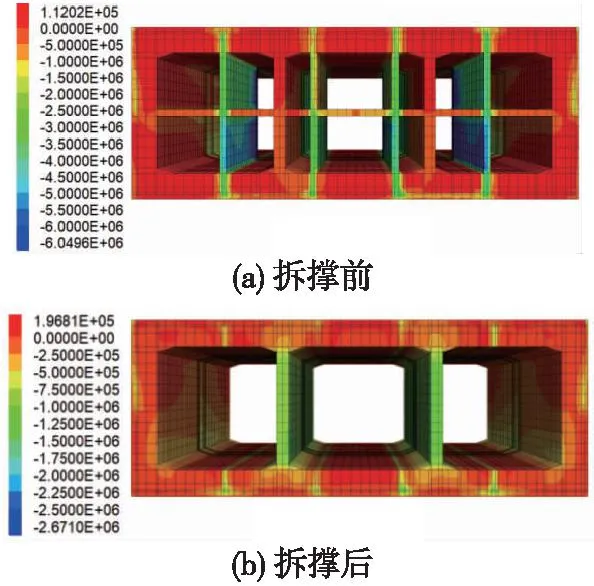
图7 “先施作二衬再拆撑”最小主应力(单位:Pa)Fig.7 Minimum principal stress of “constructing the secondary lining before dismantling lining” (unit: Pa)

图8分别为两种拆撑工况下新建通道纵向中部断面二衬顶板与初支顶板的沉降曲线。对于“先施作二衬再拆撑”工况,拆撑前后二衬顶板沉降差异较小,拆撑前后沉降差异值主要位于各竖撑位置处,拆撑后二衬最大沉降值为0.95 mm。对于“先拆撑再施作二衬”工况,沉降曲线呈现双凹槽形态,这是由于分部开挖顺序及支护时机不同导致的。拆撑后,初支顶板沉降增加明显,尤其在位于临时竖撑支承位置处的初支,拆撑后沉降变化最为显著,3号临时竖撑处拆撑后沉降值最大,达到10.30 mm,同时也是沉降突变量最大的位置,突变值为7.30 mm。

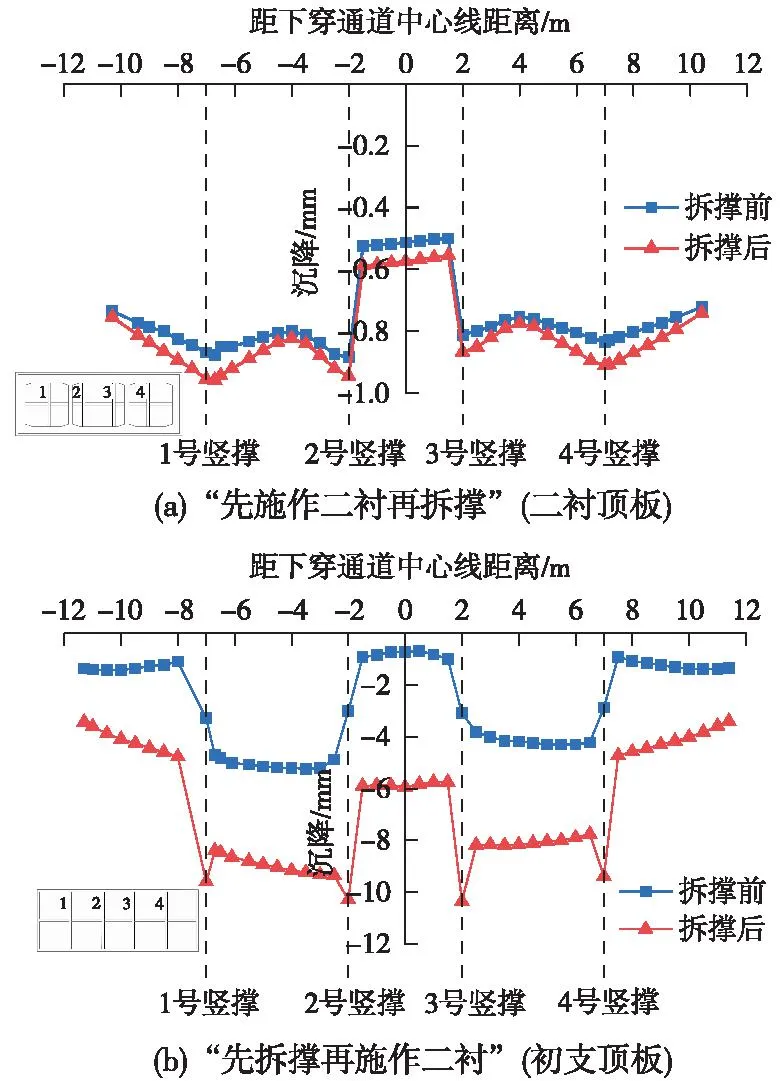
图8 新建通道顶板沉降曲线Fig.8 Settlement curve of the roof of the new underpass

3 临时支撑拆除方案分析

前文探究了依托工程实际围岩及支护参数下“先施作二衬再拆撑”和“先拆撑再施作二衬”两种工况力学差异,根据计算结果分析可知,前者工况,即在二衬施作之后进行拆撑对于既有及新建结构的影响较小。后者工况中拆撑则表现出较大的影响,拆撑行为明显改变了结构的受力变形。不难想象“先施作二衬再拆撑”对于减小拆撑风险必定是具有更大优势,但是这种方法的劣势在于施工工序繁杂,作业空间狭小,这些劣势会大大降低施工效率。而采用“先拆撑再施作二衬”施工顺序,若能尽可能减小拆撑影响,施工效率将大大提高。因此,此节将进一步研究“先拆撑再施作二衬”工况,分析考虑不同拆撑长度和拆撑方式下新建及既有支护结构的响应规律。

3.1 拆撑方式拟选

拆撑方式及拆撑长度的选择是隧道拆撑研究的重点方向[18-19],临时支撑拆除通常选用的方法为按顺序拆撑或跳仓法拆撑[20-21]。因此,本节基于“先拆撑再施作二衬”施工顺序,拟采用以上两种拆撑方式对比分析。第一种是顺序拆撑,即按照拟定的拆撑长度全断面拆撑,并及时施作二衬,再进行下一循环的拆撑与二衬施作;第二种是采用“跳仓法”拆撑,由于下穿段换乘通道长度仅有21 m,因此采取“隔一拆一”方式,本文拆撑区长度与隔仓区长度定为相同,以4 m拆撑长度为例,将换乘通道0～4 m,8～12 m,16～21 m段定为拆撑区段,4～8 m,12～16 m段定为隔仓区段,拆撑时将拆撑区段一次性拆除,然后施作此段二衬,在二衬稳定之后再一次性拆除隔仓区段临时支撑并及时施作二衬。

拟定为4,6,8 m三种工况进行分析,两种拆撑方式的具体实施步骤如表5所示。

表5 两种拆撑方式具体实施步骤Tab.5 Specific implementation steps of the two modes of dismantling lining

3.2 计算结果分析

3.2.1 既有车站底板沉降

在新建通道进行拆撑之前,将计算模型的位移进行清零处理,以分析在不同拆撑长度情况下新建通道纵向中部对应的既有车站底板沉降增量,如图9所示。采用顺序拆撑法拆撑时,拆撑长度为4,6,8 m对应的最大沉降分别为1.9,2.2,2.5 mm;采用跳仓法拆撑,对应的最大沉降增量为3.4,3.9,4.5 mm。因此,可知跳仓法拆撑引起的沉降增量远大于顺序拆撑法。

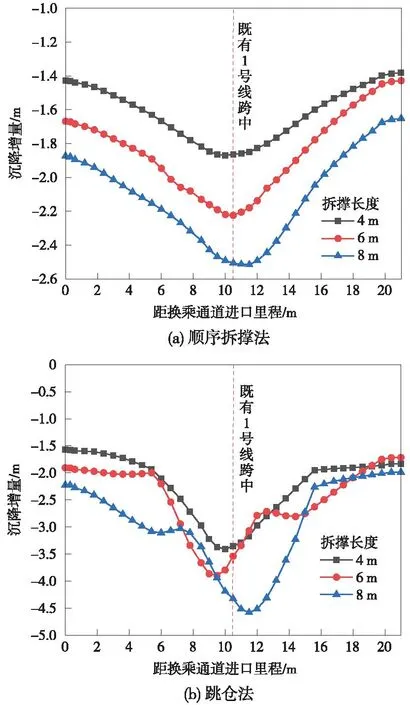
图9 既有车站底板沉降增量曲线Fig.9 Incremental settlement curve of the existing station floor

顺序拆撑法在各拆撑长度下,底板沉降增量最大位置位于既有1号线断面跨中处,跳仓法由于各拆撑长度下隔仓区间的位置不同,最大沉降位移不严格位于既有1号线断面跨中,但总体分布在跨中附近,这是由于新建通道临时支撑直接承受由1号线断面跨中柱子传下的力,因此,拆撑后沉降增量最大部位处于既有1号线断面跨中附近。

3.2.2 新建通道顶板沉降

通过前面分析可知,拆撑最不利位置位于下穿通道纵向中部,现提取各拆撑长度下新建通道顶板沉降云图,并给出下穿通道中部断面初支以及二衬最大沉降增量,如表6所示。

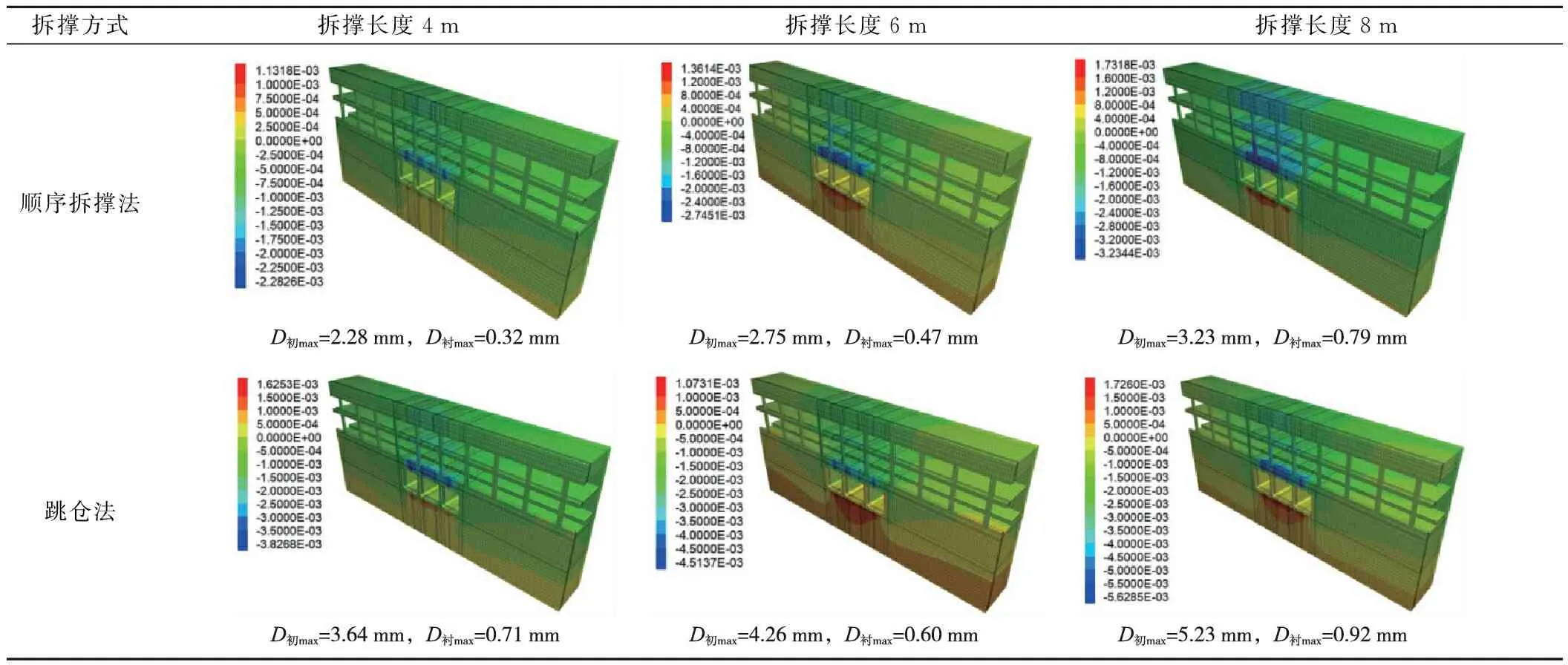
表6 下穿通道中部竖向沉降云图 mTab.6 Vertical settlement cloud picture of the middle part of the underpass

各施工步完成后,提取两种拆撑方式下穿通道纵向中部初支顶板(考察点)的沉降增量值,绘制曲线如图10所示,从图中可以明显看出,当临时支撑拆除到考察点的时候,顶板沉降增加量达到所有施工步中的最大值,此时曲线斜率也最大。顺序拆撑相比跳仓法拆撑,考察点受关键施工步(即考察点位置临时支撑拆除)的影响更小。在4,6,8 m的拆撑长度下,两种拆撑方法在关键施工步完成后的沉降突变量如表7所示。

图10 各施工步完成后新建通道初支顶板沉降增量曲线Fig.10 Settlement increment curve of the roof of the preliminary lining of the new underpass after the completion of each construction step

表7 关键施工步完成后初支顶板沉降突变量 mmTab.7 Abrupt change in the settlement of preliminary lining of roof after the completion of key construction steps

3.3 拆撑方案选择

前文中提到在拆撑计算前对模型位移进行了清零处理,着重分析拆撑这一步引起的结构沉降增量,但下穿通道前期的开挖与支护,结构已产生较大沉降,在分析总沉降时需予以考虑。

为保证施工管理的可控性,应保证新建通道上方既有地铁车站的变形值在控制管理值之内,施工现场对于既有车站结构沉降值控制在8 mm之内。两种拆撑方式下,各拆撑长度对应的既有地铁车站底板最大总沉降值如表8所示。

表8 各工况下既有地铁车站底板最大总沉降量 mmTab.8 Maximum total settlement of the floor of the existing subway station under various conditions

由表8可以看出,采取顺序拆撑方式,各拆撑长度下既有车站底板总沉降量均未超过控制值。对于跳仓法拆撑,当拆撑长度为8 m时,总沉降量为8.72 mm,已超过8 mm沉降控制值;当拆撑长度为6 m时,总沉降量为7.88 mm,已十分接近沉降控制值。因此,对于顺序拆撑法,可选取8 m的拆撑长度,其优点在于对于既有结构的影响较小,但是其施工工序略多于跳仓法,需完成6个施工步,适合于现场施工班组人员及设备较少的情况;若选择跳仓法拆撑,可选取4 m的拆撑长度,虽然仅需4个施工步,但需展开多个施工作业面同时施工,对于施工班组人员及设备数量要求高得多,若非工期严格,建议选择拆撑长度为8m的顺序拆撑方式。

4 现场监测

4.1 测点布置

现场对既有1号线的左右线4条轨道竖向沉降开展监控量测,沿1号线方向布置9个测点,测点具体分布位置如图11所示。

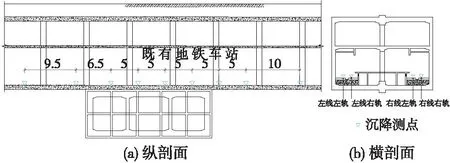
图11 沿1号线监测点布置(单位:m)Fig.11 Layout of the monitoring points along the Line 1 (unit: m)

4.2 现场测试结果

分别绘制拆撑前后的4条轨道(左线左轨、左线右轨、右线左轨、右线右轨)沿1号线方向的沉降曲线,如图12所示。可以看出,各轨道均呈现在下穿范围内沉降大,两侧沉降较小的沉降槽特征,这与数值计算得出的规律相一致。对比2.3.1节采用数值模拟方式得出的“先施作二衬再拆撑 ”工况沉降槽曲线,由于实际施工情况及影响因素更为复杂,而数值模拟考虑的是理想情况,因此,下穿段中心线两侧实测沉降量并未如数值模拟结果对称。从现场实测结果与数值计算结果均可看出,拆撑前后沉降曲线重合度较高,说明“先施作二衬再拆撑”工况下拆撑对于既有结构影响较小。从沉降量值来看,实测沉降最大值为4.89 mm,数值计算最大沉降值为4.41 mm,可知计算值与实测值具有一定的吻合性,印证了本文数值模拟的合理性,现场按照先施作二衬再拆撑的施工方法来控制沉降的效果是明显的。

图12 拆撑前后4条轨道沿1号线方向沉降曲线Fig.12 Settlement curve of 4 tracks along Line 1 direction before and after dismantling lining

5 结论

通过对比“先施作二衬再拆撑”和“先拆撑再施作二衬”两种工况下的拆撑附加影响,并基于“先拆撑再施作二衬”工况进一步分析了拆撑方案,得到以下主要结论。

(1)“先施作二衬再拆撑”工况拆撑引起既有车站弯矩及沉降增量、新建通道初支弯矩及二衬沉降增量不明显,在沉降曲线形态和弯矩沿结构横断面分布形态上,拆撑前后的差异均很小。

(2)“先拆撑再施作二衬”对于既有车站及新建通道而言影响明显,一次性全部拆撑后既有及新建结构弯矩沿断面分布形态变化显著,最大弯矩分别为41.18,46.20 kN·m,在结构沉降方面,拆撑后既有车站及新建通道初支最大沉降突变量分别达4.86,7.30 mm。

(3)基于“先拆撑再施作二衬”工况采取顺序拆撑与跳仓法拆撑,最不利区域均位于新建通道纵向中部,在4,6,8m拆撑长度下,顺序拆撑施工模拟完成后初支的沉降增量分别为2.28,2.75,3.23 mm,跳仓法分别为3.24,4.26,5.23 mm,且两种拆撑方式下二衬沉降量均未超过1 mm。