边界层和压力滞后对翼型动态失速性能的影响

李治国，陈 猛，张雅静，高志鹰，汪建文

(1.内蒙古工业大学机械工程学院，内蒙古，呼和浩特 010051；2.内蒙古工业大学能源与动力工程学院，内蒙古，呼和浩特 010051；3.内蒙古建筑职业技术学院交通与市政工程学院，内蒙古，呼和浩特 010070；4.内蒙古工业大学风能与太阳能利用技术教育部重点实验室，内蒙古，呼和浩特 010051)

动态失速是指当翼型进行俯仰或非定常周期振荡运动时，其失速攻角比翼型静止时的失速攻角要大，且翼型空气动力特性随攻角变化的曲线出现迟滞的现象[1]。翼型动态失速对风轮气动性输出及风力机正常运行时间有着非常紧密的联系[2-3]，探究翼型动态失速机理及动态失速发生后对风轮气动性能的影响逐渐成为国内外学者研究的热点。

梁湿[4]和雷航[5]分别利用修正后的B-L 模型与B-L 简化模型得到平均攻角、马赫数、时间常数等对动态失速的影响规律，发现时间常数在一定变化范围内，增加压力滞后时间常数可以提高最大升力系数，而增加边界层滞后时间常数则可以提高动态失速攻角。杨鹤森等[6]分析翼型型面等参数对动态失速的影响，并对常见的动态失速流动控制方法及其研究现状进行总结。孙翀等[7]采用本征正交分解方法 (proper orthogonal decomposition, POD)对S809 翼型静态失速与动态失速非定常压力场的主要流动模态进行提取，并结合POD 系数对非定常流动进行分析。RUAN 和HAJEK[8]通过对单个旋转和俯仰叶片进行了数值研究。研究了Ω形动态失速涡流、前缘涡与尖端涡旋的相互作用。刘雄等[9]对B-L 模型的分离点和动态攻角进行改进，并加入涡流对切向力的影响，使大攻角时切向力的模拟更接近实验值。胡智等[10]通过对CFD (computational fluid dynamics)计算结果动力模态分解(dynamic mode decomposition,DMD)的方法，分析平均攻角、振荡幅度和折合频率对翼型动态失速流场的影响。TIRANDAZ 和REZAEIHA[11]、BANGGA 等[12]针对垂直轴风力机，分别分析翼型形状与厚度对动态失速的影响。刘鹏寅等[13]采用DMD 方法，直观地表达振荡翼型在深度动态失速下非定常流场的演化过程，揭示深度动态失速下复杂流场中不同尺度的相干结构及其相互作用。戴玉婷等[14]对标准L-B非线性非定常气动力模型进行马赫数修正，并通过二元翼段失速颤振风洞试验验证修正模型的准确性，使其适用于低速不可压情形的动态失速气动力计算。高超等[15]利用有限元软件结合风洞试验探究相对厚度对翼型气动性能影响，得到相对厚度对气动性能的影响规律。ROCCHIO 等[16]主要研究俯仰翼型的动态失速行为，并针对深失速状态提出一种计算复杂度低，但能处理包括前缘多涡脱落等不同类型的失速模型。HUANG 等[17]利用Fluent 软件计算得到静态与动态参数，并与改进后的B-L 模型相结合来预测翼型的动态失速特性，为风力机动态载荷的预测提供了一种更简单可行的新方法。

国内外专家学者对风力机翼型动态失速做了大量研究，分析了翼型形状、厚度、平均攻角、衰减频率等影响因素对动态失速的影响。行业内主流动态失速模型多为半经验模型，经验常数的准确性对模型精度有较大影响，但鉴于压力滞后和边界层滞后对动态失速影响机理的复杂性，相关研究较少。本文基于丹麦国家实验室建立的B-L简化模型[18]，以S809 翼型为算例，探究压力滞后时间常数与边界层滞后时间常数对动态升力系数与动态阻力系数的影响。并结合内蒙古工业大学风能太阳能利用技术教育部重点实验室风洞实验数据，调整压力滞后与边界层滞后时间常数的值，以提高B-L 简化模型的计算精度。

1 动态失速模型

1.1 动态升力系数

1.1.1 附着流

风力机翼型在进行俯仰运动时，通过Theodorsen 理论可近似得到翼型的非定常升力，假设尾缘涡流是简谐波且涡脱落后自由流动轨迹为直线运动，如图1 所示。

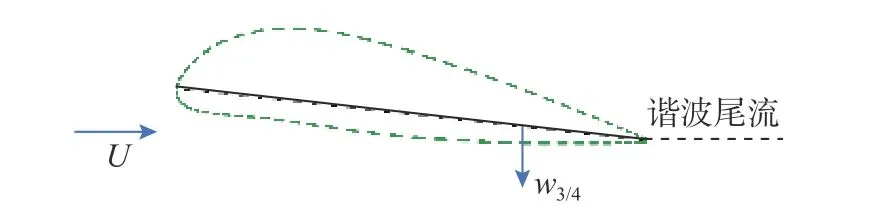
图1 Theodorsen 理论假设示意图Fig.1 Schematic of assumptions of the Theodorsen theory

当空气为附着流动时，通过式(1)得到空气动力学状态变量，确定附近尾流对非稳态升力系数的动态影响。但在大攻角范围内下洗气流定义模糊，公式内使用复杂，故在B-L 模型中通常使用翼型弦向3/4 处攻角a3/4代替下洗气流ω3/4[18]。

式中：i=1,2；yi(0)=0；Tu=c/2U；A1、A2、b1、b2为时间常数；h˙为翼型颠簸运动加速度；α为攻角； α˙为攻角变化速率；c为翼型弦长；U为来流风速。利用式(1)与式(3)可以得到附着流的状态变量[18]：

由状态变量x1、x2可以得到有效攻角 αE，进而得到附着流的非稳态升力系数：

1.1.2 分离流

通过基尔霍夫流动理论[19-20]可以得到分离点位置与翼型静态升力系数的关系[18]：

式中：CL,a为静态升力系数曲线线性部分斜率；函数fst(α)为翼型后缘分离点位置函数，如图2 所示。

图2 翼型后缘分离点Fig.2 Trailing edge separation point

当气流完全附着在翼型表面，即完全附着流时，fst=1，而当气流从前缘开始与翼型表面分离，即完全分离流时，fst=0，由于分离点不能超出翼型的前缘及后缘，0≤fst≤1。静态升力系数曲线中线性部分的斜率CL,a[18]：

由已知的翼型静态升力系数，通过式(7)的转换，可以得到翼型分离点函数[18]：

令式(9)中fst=0， 即(α±f s)=|CL,a(α±f sα0)|/4，得到翼型上、下表面的完全分离攻角α+f s和α-f s，当攻角超出α±f s范围时，式(9)失效，fst被置为0，静态升力系数曲线通过式(10)，由完全附着流升力系数CL,a(α-α0)fst与完全分离流升力系数(α)(1-fst)插值得到[18]：

在B-L 简化模型中，以状态变量x3与x4对后缘分离的动态特性进行描述，由于翼型所产生的升力由翼型上的压力分布决定，而翼型上的压力分布又与流动分离息息相关，翼型上的压力与升力存在一个时间滞后关系，即压力滞后[18]：

式中：x3初始值为0；Tp为压力滞后时间常数。

状态变量x3即附着流升力系数的时间滞后量，利用考虑压力滞后的升力系数，通过式(13)，得到准静态攻角 αf与准静态分离点f′[18]：

状态变量x4用于描述边界层的动态特性，即非稳态分离点f′′。由于边界层上动力学导致分离点滞后于稳态分离点f′，需引入一个边界层时间滞后常数，式(14)表示动态分离点与准静态分离点的滞后关系[18]：

式中：x4初始值为0；Tf为边界层滞后时间常数。

通过式(10)，在考虑式(6)附加质量力影响的同时得到考虑后缘分离影响的非稳态升力系数[18]：

1.2 动态阻力系数

动态阻力由诱导阻力、粘性阻力2 部分组成，其中：诱导阻力是由尾流诱导的下洗速度造成的有效升力攻角的变化，从而诱导出的阻力项；粘性阻力则是由粘性边界层引起的，由摩擦阻力和压差阻力两部分组成[5]。

1.2.1 诱导阻力

非稳态时，由于后缘存在脱落涡的影响，有效攻角 αE与几何攻角存在滞后关系，此时非稳态升力与有效攻角 αE垂直，所以在由几何攻角定义的阻力方向，非稳态升力会产生一个诱导的项，如图3 所示。诱导阻力系数为[18]：

图3 诱导阻力示意图Fig.3 Schematic diagram of induced drag

1.2.2 粘性阻力

在边界层位置由于空气的流动会产生一个粘性阻力，当空气为附着流动时，通常将其视作恒定的摩擦阻力；当空气为分离流动时，由于压差阻力的原因，粘性阻力会显著增大，此时边界层内压力相对于附着流动时更低，通过对翼型表面的压力求和，得到在阻力方向上的一个分力项[18]：

动态失速模型整体流程如图4 所示。

图4 动态失速模型计算流程图Fig.4 Calculation flow chart of dynamic stall model

2 结果分析

2.1 模型验证

通过文献[21 - 23]可知，时间常数A1=0.3，A2=0.7，b1=0.14，b2=0.53，压力滞后时间常数Tp=1.7，边界层滞后时间常数Tf=3。以雷诺数1×106下S809 翼型为算例，通过上述模型分别对动态失速下升力系数、阻力系数进行计算分析，其中风力机翼型在进行俯仰运动时，通过Theodorsen理论可近似得到翼型的非定常升力，而B-L 简化模型中在计算动态升力系数中以Theodorsen 理论为基础，研究动态附着流的影响，故将攻角设置为周期性运动[24-25]，攻角变化可表示为：

式中：A为平均攻角；B为攻角幅值；k为衰减频率，可表达为k=(ϖc)/(2U)。

为了验证本文模型准确性，在实验室内的B1/K2 低速直流式风洞闭口实验段进行实验，风洞全长 24.59 m，最高稳定风速 20 m/s，实验叶片通过螺栓与旋转台连接，旋转台通过联轴器、减速器与伺服电机相连，利用驱动器对伺服电机进行控制，实现叶片攻角的周期性运动，叶片上压力传感器信号经压力采集系统输入计算机进行时均处理和积分计算得到叶片动升阻力系数。实验设备如图5 所示。

图5 风洞实验设备Fig.5 Wind tunnel test equipments

翼型摆动周期包括平均攻角A=8°、攻角幅值B=5°、衰减频率k=0.033，雷诺数为1×106工况为例，分别通过模型与实验进行计算，重复实验以获取多组数据，并选择其中重复度最高的数据进行对比分析，以尽可能地消除误差带来的影响。模型计算结果与实验数据对比如图6 所示，动态失速模型计算结果与实验数据吻合良好，证明本动态失速模型具有良好的可靠性，数值计算结构具有较高可信度。但动态升力系数部分模型计算结果略大于实验结果，故需对模型进一步改进，提高模型的准确性。

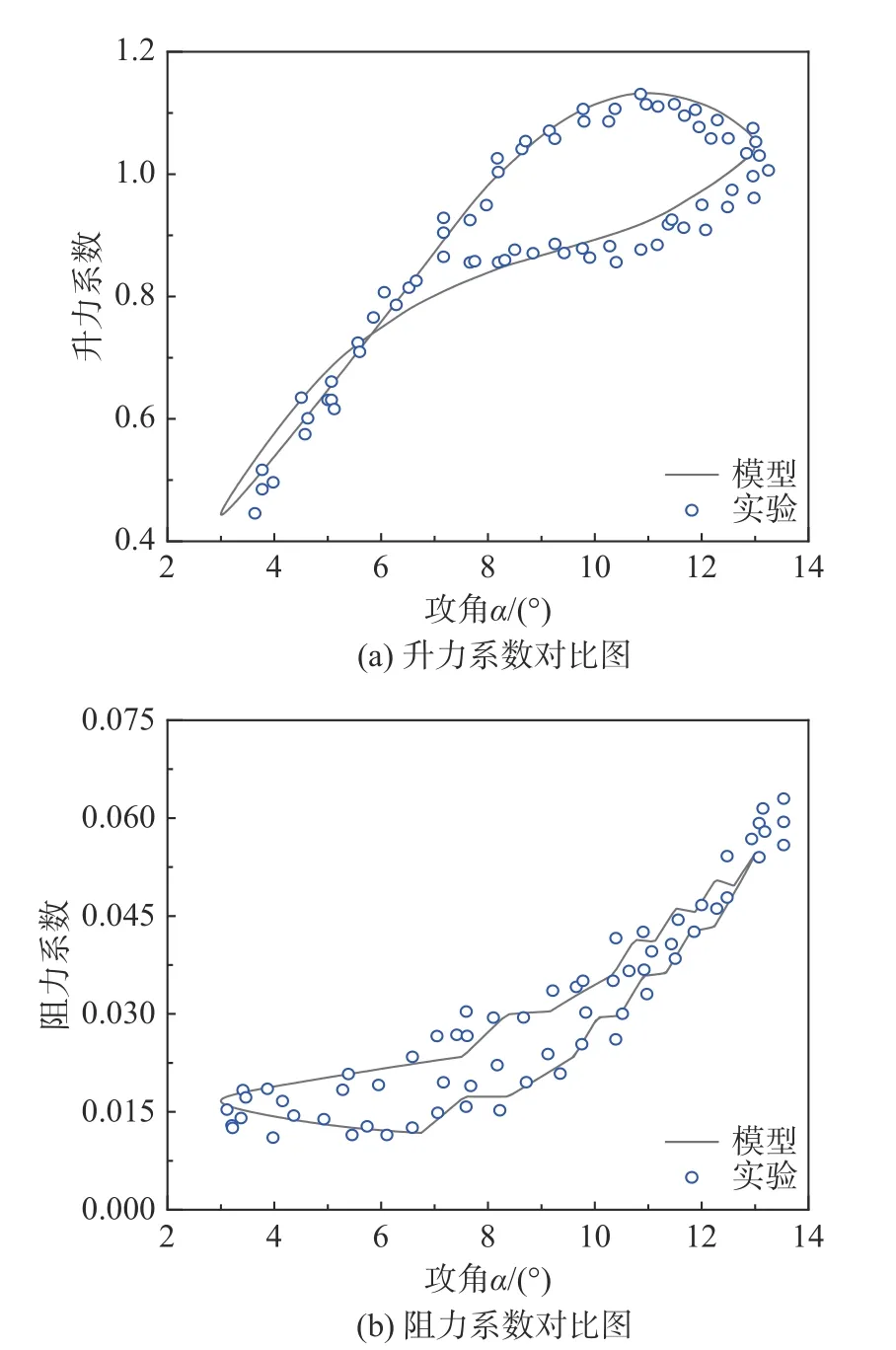
图6 S809 翼型模型计算与实验数据对比图Fig.6 Comparison between model calculation and experimental data of S809 airfoil

2.2 算例分析

利用1.1 节、1.2 节建立的动态失速模型结合风洞实验，以S809 为算例，通过对式(7)～式(11)的计算可以得到分离点函数，进而得到翼型的完全附着流升力系数与完全分离流升力系数，如图7所示。通过对分离点函数的分析，可知在小攻角时，气流完全附着在翼型表面；随着攻角的增大，气流开始与翼型吸力面后缘处出现分离，此时为轻度失速；当攻角进一步增大，分离点由翼型后缘向前缘移动，直至与吸力面完全分离，此时为深度失速。为探究经验常数对动态失速性能的影响，优化动态失速模型经验常数，选取如表1所示的轻度失速与深度失速两种工况，在衰减频率k=0.025 时，分别改变压力滞后时间常数与边界层滞后时间常数，分析不同攻角范围下，压力滞后时间常数与边界层滞后时间常数对动态升力系数与动态阻力系数的影响。

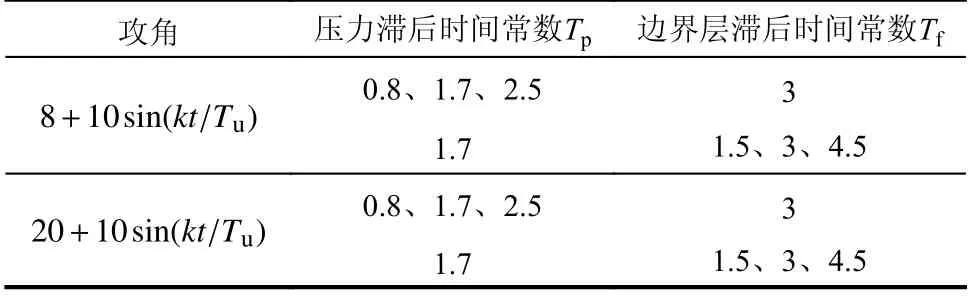
表1 计算工况参数表Table 1 Calculation condition parameters

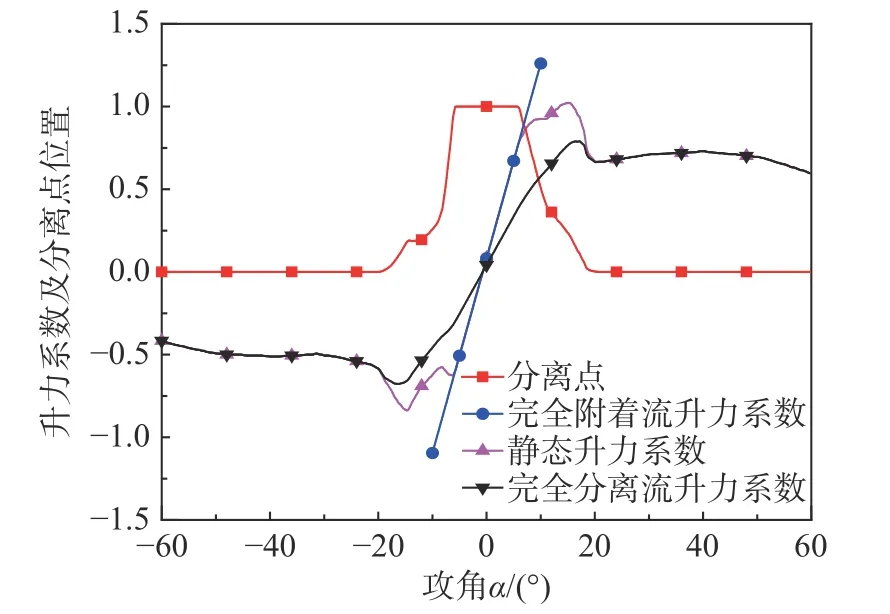
图7 S809 翼型静态升力系数各项与分离点函数图Fig.7 Function diagram of static lift coefficient and separation point of S809 airfoil

2.2.1 压力滞后时间常数的影响

图8、图9 为不同攻角变化范围下，压力滞后时间常数对动态升力系数、动态阻力系数影响的变化曲线。如图8(a)所示，在攻角较小，气流附着流动时，压力滞后时间常数的改变对升力系数的大小几乎不会产生影响；随着攻角的增大，气流开始与翼型出现分离，此时动态升力系数随着压力滞后时间常数的增大而增大；当攻角由最大值逐渐减小到最小值时，压力滞后时间常数的改变对升力系数的大小几乎不产生影响。如图9(a)所示，随攻角的逐渐增大，翼型上气流由分离动至完全分离流动，动态升力系数随着压力滞后时间常数的增大而增大；当攻角由最大值逐渐减小到最小值的过程中，在气流处于完全分离流动时，压力滞后时间常数的改变对升力系数的大小影响较小；而当气流处于分离流动时，动态升力系数随着压力滞后时间常数的增大而减小。如图8(b)、图9(b)所示，压力滞后时间常数对动态阻力系数的影响可忽略不计。

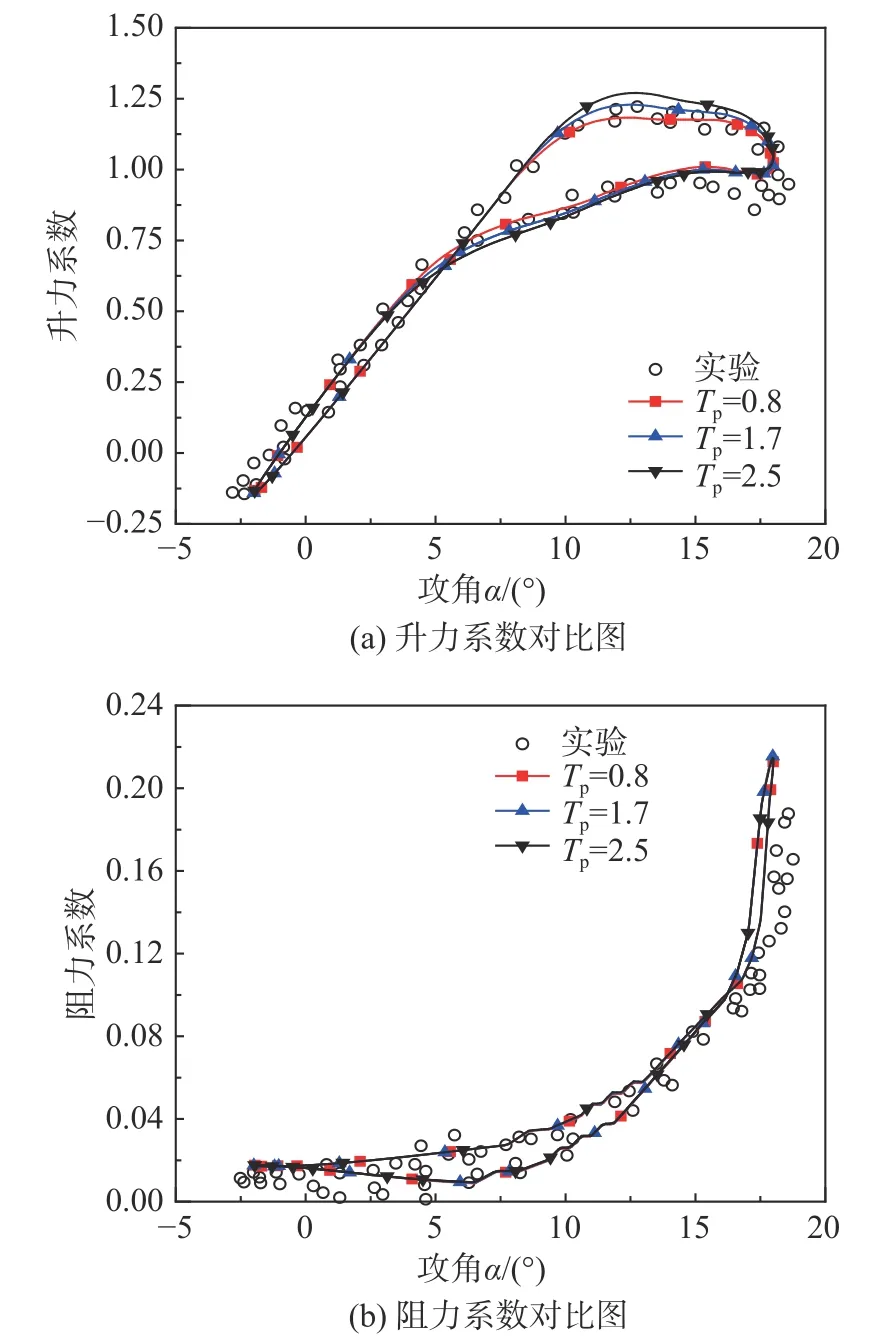
图8 8+10sin(kt/Tu)攻角下压力滞后的影响Fig.8 Effect of pressure lag at angle of attack of8+10sin(kt/Tu)

图9 20+10sin(kt/Tu)攻角下压力滞后的影响Fig.9 Effect of pressure lag at angle of attack of 20+10sin(kt/Tu)

由动态失速模型模拟值与实验数据相对比可知，当平均攻角相对较小，气流处于附着流动与分离流动时，相对于文献[22 - 23]可适当减小Tp的值，使动态失速模型计算结果更接近实验值。当平均攻角相对较大，气流处于分离流动与完全分离流动时，可适当增大Tp的值。

2.2.2 边界层滞后时间常数的影响

图10、图11 为不同攻角变化范围下，边界层滞后时间常数对动态升力系数、动态阻力系数影响的变化曲线。如图10(a)所示，当气流为附着流动时，边界层滞后时间常数的改变对升力系数几乎不会产生影响；当气流与翼型出现分离时，在攻角增大过程中动态升力系数随着边界层滞后时间常数的增大而增大，攻角减小时，动态升力系数随着边界层滞后时间常数的增大而减小。如图11(a)所示，随攻角的逐渐增大，翼型上气流由分离动至完全分离流动，动态升力系数随着边界层滞后时间常数的增大而增大；当攻角由最大值逐渐减小到最小值的过程中，在气流处于完全分离流动时，边界层滞后时间常数的改变对升力系数的大小影响较小，而当气流处于分离流动时，动态升力系数随着边界层滞后时间常数的增大而减小。如图10(b)所示，边界层滞后时间常数对动态阻力系数的影响可忽略不计。如图11(b)所示，边界层滞后时间常数对动态阻力系数的影响不大，仅在攻角逐渐减小的完全分离流动过程中，动态阻力系数随着边界层滞后时间常数的增大而减小。

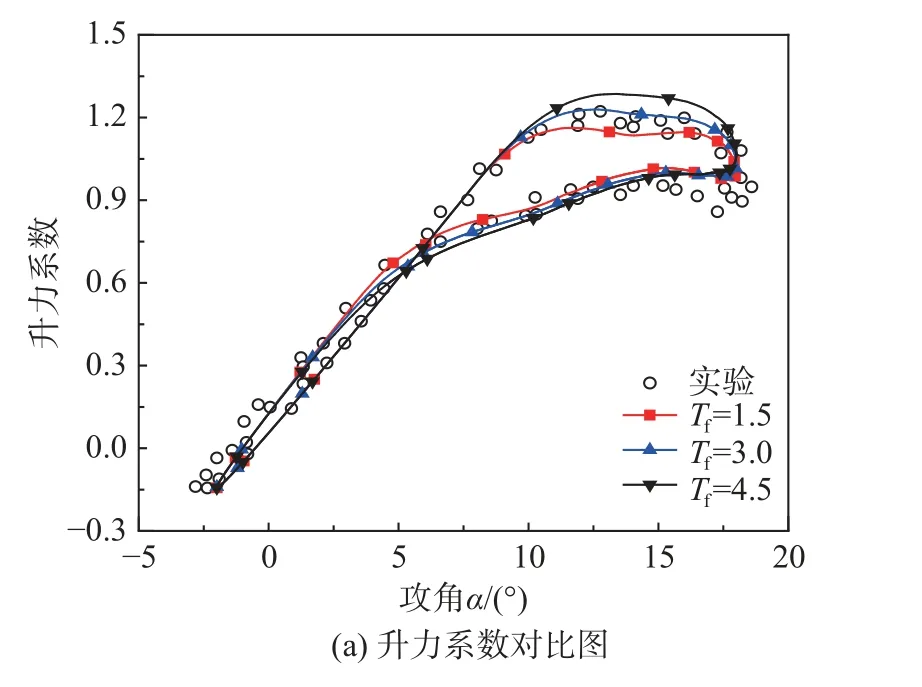
图10 8+10sin(kt/Tu)攻角下边界层滞后的影响Fig.10 Effect of boundary layer lag under angle of attack of 8+10sin(kt/Tu)

图11 20+10sin(kt/Tu)攻角下边界层滞后的影响Fig.11 Effect of boundary layer lag under angle of attack of 20+10sin(kt/Tu)

由动态失速模型模拟值与实验数据对比可知，当平均攻角相对较小，气流处于附着流动与分离流动时，相对于文献[22 - 23]可适当减小Tf的值，使动态失速模型计算结果更接近实验值。当平均攻角相对较大，气流处于分离流动与完全分离流动时，可适当增大Tf的值。

3 结论

本文基于B-L 简化模型，以S809 翼型为算例，探究压力滞后时间常数与边界层滞后时间常数对动态升力系数与动态阻力系数的影响。并结合内蒙古工业大学风能太阳能利用技术教育部重点实验室风洞实验数据，通过改变时间常数的值，提高B-L 简化模型的计算精度，结论如下：

(1) 时间常数的大小对动态升力系数的影响较大且与失速程度有关。气流发生流动分离且攻角增大时动态升力系数随时间常数的增大而增大，攻角减小时动态升力系数随边界层滞后时间常数的增大而减小。在深度失速中，攻角增大过程中动态升力系数随时间常数的增大而增大，攻角减小过程中动态升力系数随时间常数的增大而减小。

(2) 适当改变时间常数的大小可以使动态失速模型计算结果更接近实验值。当平均攻角相对较小，气流处于附着流动与分离流动时，可适当减小时间常数的值，使动态失速模型计算结果更接近实验值。当平均攻角相对较大，气流处于分离流动与完全分离流动时，可适当增大时间常数的值。

(3) 压力滞后时间常数与边界层滞后时间常数的改变对动态阻力系数的影响不大。动态升力系数仅在攻角逐渐减小的完全分离流动过程中，随着边界层滞后时间常数的增大而减小。

本文仅对S809 翼型进行分析，未分析其他翼型以验证结论的普遍性，且并未计算S809 翼型的最佳压力滞后常数和边界层滞后时间常数。