基于SMCS 模型的高强螺栓及节点火灾全过程断裂性能模拟
陈 桥,姜 健,蔡文玉,陈 伟,叶继红
(1.中国矿业大学力学与土木工程学院,江苏,徐州 221116;2.海南大学土木建筑工程学院,海南,海口 570228)
钢节点作为钢结构构造和承载力设计的关键区域,其断裂失效问题受到广泛关注,建立合理的钢材断裂模型,进行高效、准确的数值模拟是钢节点性能研究和工程设计的重要途经。
近年来,微观断裂模型被广泛应用于常温下钢材断裂性能和梁柱焊接节点断裂问题研究[1-11]。MYERS 等[1]应用SMCS 模型预测A36 钢的断裂问题,建立了考虑材料本构、试件几何形状和变形量的半经验公式,用于直接根据拉伸试验数据确定SMCS 模型参数;周晖等[2]对7 种梁柱节点局部焊接试件开展拉伸试验,校准了Q345 钢VGM模型、SMCS 模型参数,发现两种模型预测焊接节点延性启裂的准确性较好,优于传统断裂力学方法;廖芳芳等[3]设计了代表不同应力三轴度的拉伸试件,常温试验研究发现,Q460D 钢的断裂应变随应力三轴度的升高呈指数形式下降,基于Rice-Tracey 理论校准和验证了其延性断裂模型;刘希月等[4]和王元清等[5]针对Q235B、Q345B、Q460C钢开展了试验研究,获得了三种钢材的VGM 和SMCS 模型参数,发现两种模型韧性参数与试件的塑性有关,材料塑性越好,模型韧性参数值越大;CAI 等[6]进行了国产高强钢(Q460、Q550、Q690、Q890)和欧洲高强钢(S460、S690和S960)火灾后SMCS 模型的校准工作,揭示了模型参数与峰值温度的变化关系。
火灾是建筑结构最常见、最具危害性的灾害之一。火灾下钢梁悬链线效应产生的附加拉力易造成梁柱节点断裂破坏,导致整体结构发生连续性倒塌。目前,梁柱节点高温力学性能研究已取得了一定进展[12-19]。SPYROU[12]研究了温度、构件几何尺寸和材料强度对T-stub 节点力学性能的影响,发现了高温下T-stub 节点的三种失效形式;余红霞[13]进行了普通钢节点高温破坏试验,结果表明,随着温度的升高,节点破坏模式由钢材构件向螺栓转换;舒赣平等[14]对T-stub 节点进行火灾试验,发现T-stub 节点火灾中的失效模式取决于受拉区T 型钢和高强螺栓间的相对承载力;BARATA 等[15]研究了翼缘板厚度、螺栓强度等级和直径对T-stub 节点高温下(500 ℃、600 ℃)力学性能和延性的影响;蔡文玉和李国强[16]对20 ℃~700 ℃下焊脚尺寸相同的角焊缝焊接接头的断裂模式开展研究,采用HOOPUTRA 等[20]提出的剪切断裂理论模型,校准了适用于焊材熔敷金属的高温剪切断裂模型材料参数,指出在高温下(大于500 ℃)焊材断裂参数是其常温值的4.5 倍。
关于钢结构节点断裂失效破坏研究,研究对象集中于钢材和焊接节点,缺少对螺栓连接断裂性能研究;温度条件主要包括常温、火灾升温段,缺少降温段和火灾后研究,尤其缺乏微观断裂模型在火灾降温段和火灾后的适用性研究。在火灾降温段,钢梁发生收缩,易引起梁柱节点受拉破坏,研究火灾升-降温全过程下钢结构节点破坏行为更具有实际工程意义。
本文采用SMCS 断裂模型表征火灾全过程下(升温段、升温-降温段、火灾后)10.9 级高强螺栓在不同高应力三轴度下的断裂行为,基于已有高强螺栓拉伸试验结果,结合有限元模拟,对模型参数进行校准;通过螺栓高温拉伸断裂试验和T-stub 节点高温断裂试验验证SMCS 模型的适用性和准确性;采用经过验证的数值模型进行参数分析,研究损伤准则和温度历程对T-stub 节点火灾全过程断裂行为的影响。
1 微观断裂模型
延性金属材料微观断裂机理主要包括以下3 种:① 孔洞形核-扩张-贯通机制(受拉状态);② 剪切型机制(受剪或受压状态);③ 孔洞-剪切复合型机制(拉剪状态)。基于临界塑性应变的概念可以建立微观断裂模型,判定当某一点在某一时刻的等效塑性应变达到临界应变时发生断裂,不同断裂模型的区别主要在于应变状态函数的影响因素及其数学表达。VGM 模型、SMCS 模型和Johnson-Cook 模型是最常见的三种微观断裂模型,相应断裂判据见表1。1969 年,RICE 和TRACEY[21]假定孔洞为一独立的球形腔体,提出孔洞扩张速率和应力三轴度之间存在指数关系:

表1 三种常见断裂模型及断裂判据Table 1 Three common fracture models and fracture criteria
式中:Rv为瞬时孔洞半径;C1、C2为材料参数;η 、 εp分别为某点的应力三轴度和等效塑性应变。
考虑到延性断裂是一个连续的过程,KANVINDE和DEIERLEIN[22]通过对RICE 和TRACEY[21]提出的指数关系(式(1))在塑性加载历程上进行显式积分,得到断裂全过程的累积孔洞扩张量,即VGM模型的断裂判据(式(2)),当累积孔洞扩张量达到临界值时发生延性断裂。VGM模型由于需要对应力应变过程进行积分,计算程序复杂繁琐。
式中:Rv0为初始孔洞半径;Rvc为临界孔洞半径;εp,critical为临界塑性应变。
此后,HANCOCK 和MACKENZIE[23]将VGM模型中积分号内的项单独提出作为孔洞扩张的控制函数,建立一种应力三轴度恒定的断裂模型,即SMCS 模型(式(3)),该模型假定应力三轴度不随等效塑性应变改变。VGM、SMCS 模型均同时考虑了塑性应变和应力三轴度对孔洞扩张的影响,可认为SMCS 模型是对VGM 模型的一种简化,其最终形式如式(4)所示。
式中,C3、 α 和 β均为材料参数。
1985 年,JOHNSON 与COOK[24]提出了一种同时考虑应力三轴度、应变速率和温度的断裂模型(Johnson-Cook 模型)。相比其他两个模型,Johnson-Cook 模型精度更高,但需要标定5 个参数,增加试验工作量。鉴于此,本文采用SMCS 模型(式(4))对火灾全过程下10.9 级高强螺栓在高应力三轴度下的断裂行为进行预测,基于螺栓试验数据校准模型参数,并应用于T-stub 节点断裂模拟。
2 SMCS 模型参数校准
2.1 断裂试验
为校准SMCS 模型参数,对不同应力三轴度10.9 级高强螺栓试件开展了火灾全过程(升温段、升温-降温段、火灾后)拉伸试验,初始应力三轴度根据式(5)计算[25]。其中,平滑圆棒初始应力三轴度为0.333,为了考虑高应力三轴度,即不考虑螺栓受剪切(拉剪)工况,仅考虑螺栓受单轴拉伸或多轴拉伸工况,为后续校准断裂模型参数提供试验数据,在标距范围内预设两种不同大小的缺口:缺口半径6 mm(初始应力三轴度为0.556)和缺口半径3 mm (初始应力三轴度为0.739),两种缺口试件的根部截面半径同为3 mm,如图1(b)所示。采用恒温加载制度进行试验,设定以200 ℃为温度梯度进行升温和降温,共计11 个温度工况(表2),火灾后试验的最高温度达800 ℃,而升温试验最高温度仅为600 ℃,这是受限于中型高温炉的温控限制。稳态拉伸控温曲线如图2 所示。同步触发拉伸试验机和DIC 测量系统,得到试件真实应力和真实应变,DIC 测量的关键信息:① 颈缩处瞬时截面积,以此计算真实应力;② 颈缩处表面平均轴向应变,获取接近断裂时刻图像中颈缩区域的纵向平均应变[26],作为真实应变。具体试验细节见文献。整理得到的真实应力-塑性应变曲线如图3 所示。每个断裂时刻的数据点由实心方块标出,括号内数值依次表示相应的塑性应变和真实应力。火灾全过程下10.9 级高强螺栓各力学性能指标见表3。
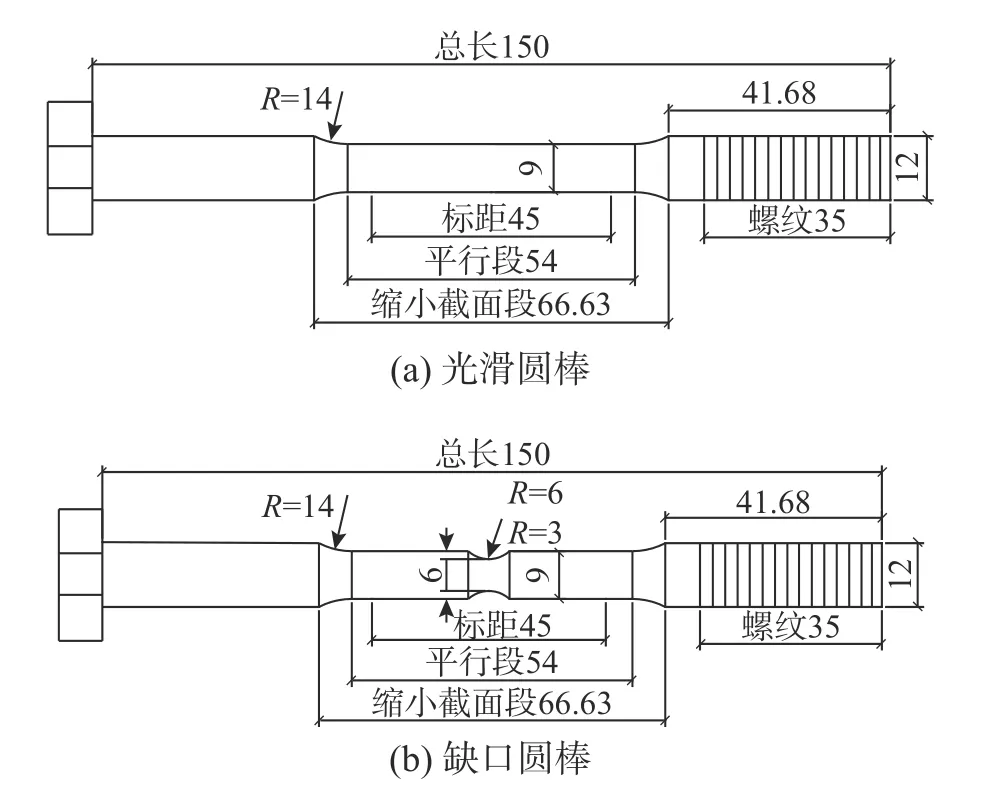
图1 拉伸螺栓试件尺寸 /mmFig.1 Size of tensile bolt specimens
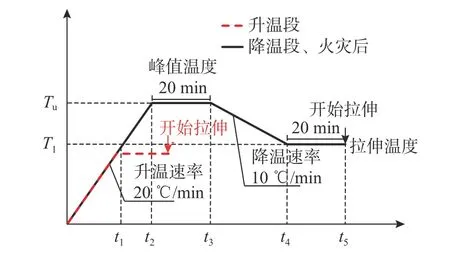
图2 火灾全过程稳态拉伸控温曲线Fig.2 Steady state tensile temperature control curves in the whole process of fire

图3 螺栓真实应力-塑性应变曲线Fig.3 True stress-plastic strain curves of bolts
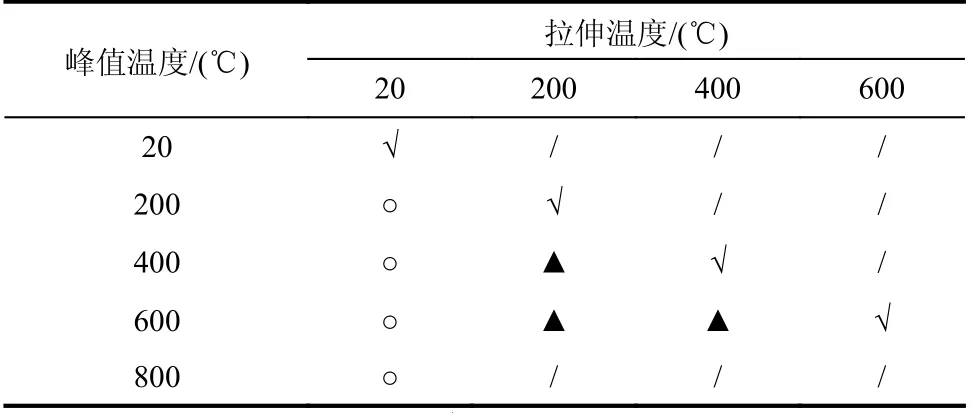
表2 试验温度工况Table 2 Test temperature and working conditions
式中: η0为初始应力三轴度;a为根部截面半径;R为试件缺口半径。
2.2 有限元模拟
2.2.1 有限元模型
在有限元软件ABAQUS 中建立试件的有限元模型,如图4 所示。采用实体单元C3D8,对于应力集中容易发生断裂的部位,网格尺寸取1 mm,其他部位网格尺寸取3 mm~5 mm;边界条件为一端固结,一端施加位移。在试件沿中轴线位置距中点左、右各12.5 mm 处分别设置一个参考点(与试验引伸计范围对应)。将图3 的真实应力-塑性应变曲线输入每组温度工况的3 个模型中,采用显式动力分析,同时考虑大变形和几何非线性,根据数值模拟输出的位移及加载点的反力,可计算得到试件的工程应力-应变曲线。

图4 螺栓试件的有限元模型Fig.4 Finite element models of bolt specimens
2.2.2 网格尺寸敏感性分析
本文以常温光滑圆棒试件为例,考虑其模型断裂部位网格尺寸在0.25 mm~2 mm 变化,数值预测和试验获得的工程应力-应变曲线对比如图5 所示。结果表明:单元网格尺寸的增加会使应力较大区域的单元平均应力计算值偏小,导致断裂时刻延后。同时,增大网格尺寸引起单元数量的逐步减少,使螺栓起裂和裂纹扩展发生突然,导致动力效应增大。网格尺寸为2 mm 的模型与1 mm的模型相比,起裂点和裂纹扩展的结果有明显偏差。网格尺寸1 mm 与0.5 mm、0.25 mm 的预测结果差异变得相对较小,对起裂点应变的预测差异在2%以内,说明当网格尺寸小于1 mm 时达到收敛。因此,本文螺栓的模型网格尺寸均采用1 mm。
2.2.3 应力三轴度与等效塑性应变的关系
校准断裂模型参数前,取各试件最小截面处中心点作为起裂点[27],得到该点处应力三轴度和等效塑性应变的变化关系(以常温为例,如图6 所示)。随着等效塑性应变的增大,应力三轴度先增大后减小,加载过程中试件的应力三轴度变化不规律,尤其在等效塑性应变低于0.1 时,应力三轴度值出现极不稳定的跳跃现象。因此,应力三轴度取值时应尽可能考虑整个加载历程的影响,本文采用式(6)计算应力三轴度在断裂应变上的积分,即等效应力三轴度。采用起裂点的等效应力三轴度和等效塑性应变校准断裂模型。

图6 螺栓试件应力三轴度-等效塑性应变曲线Fig.6 Stress triaxiality-equivalent plastic strain curves of bolt specimens
式中, εf为等效塑性应变。
2.2.4 参数校准
采用式(4)所示的SMCS 模型表征高强螺栓的断裂行为,为了确定等效应力三轴度和临界塑性应变εp,critical的数值关系,需要确定两个与材料相关的参数 α 和 β 。 α参数表示韧性指标,是对断裂起裂阻力的量化[22];对于一般钢材, β通常在1.5~2.4 取值[24]。各试件断裂时刻的位移 Δf、结合有限元输出结果计算得到的等效应力三轴度和临界塑性应变εp,critical,和最终拟合确定的两个模型参数见表4,同一工况下的同种试件,值离散系数能够实现控制在10%以内,说明SMCS 模型适用于预测高强螺栓在火灾全过程下的断裂行为。
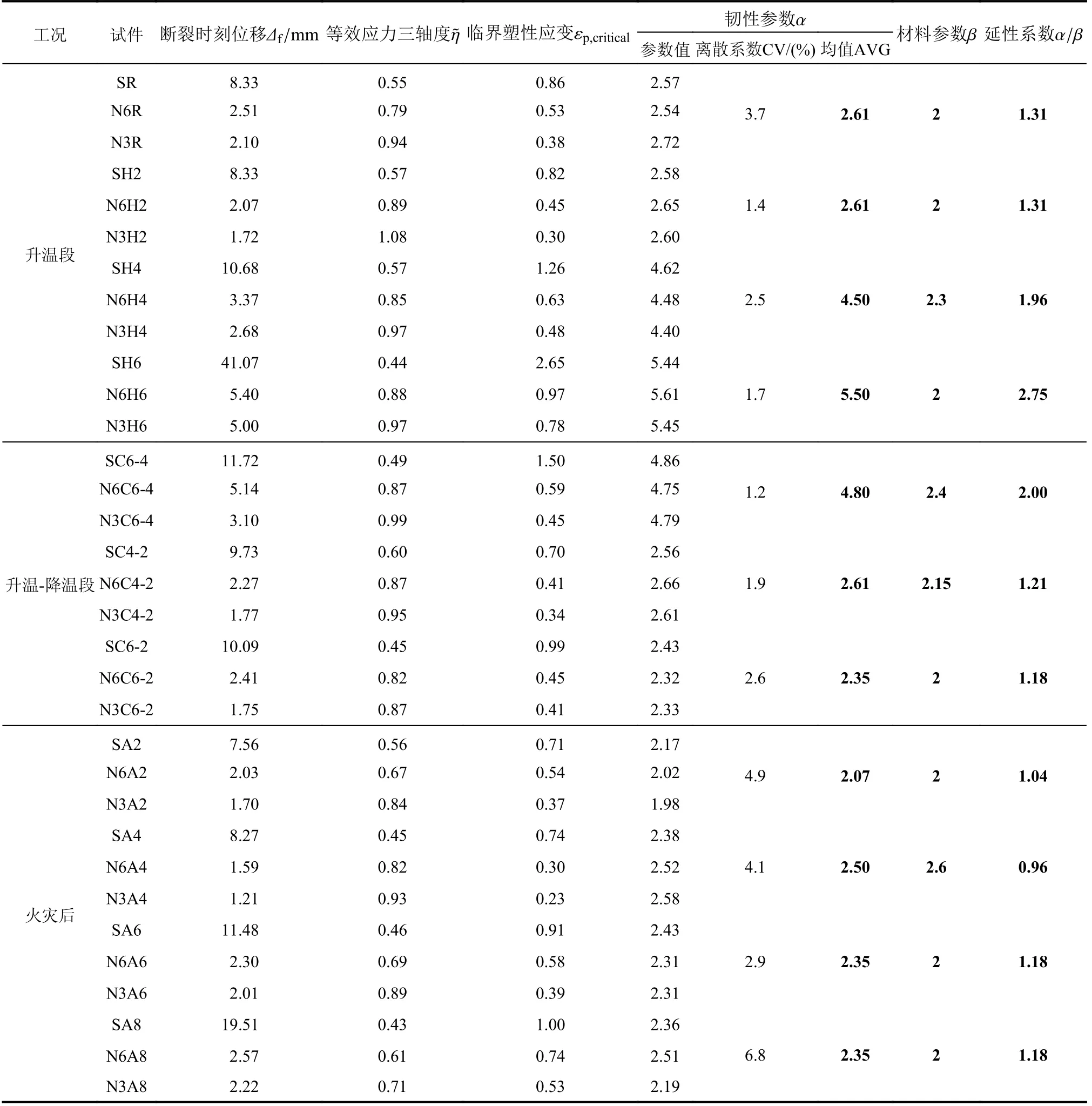
表4 SMCS 模型参数校准Table 4 Parameter calibration of the SMCS model
表4 中试验结果和数值拟合结果的对比如图7(a)~图7(c),在高应力三轴度(受拉状态)下,临界塑性应变随应力三轴度的增长呈指数型降低。本文螺栓试件的初始应力三轴度的范围为0.33~0.74,图7 中数值分析得到的试件应力三轴度范围为0.3~1.2,以下标定SMCS 模型选取图7所示的应力三轴度范围,即为模型的适用范围。由于参数 α与材料抗断裂性能成正相关, β与材料抗断裂性能成负相关,取两者比值 α / β综合评估所有工况在高应力三轴度下的断裂性能,如图7(d)所示。受温度影响,高强螺栓抗断能力发生变化(图7(d)):1)对于升温段,200 ℃以下的温度基本不影响螺栓抗断能力。但高于400 ℃时,抗断能力随温度线性增长,温度400 ℃、600 ℃下分别提高到常温值的1.5 倍和2.1 倍;2)在升温-降温段,工况600 ℃~200 ℃与400 ℃~200 ℃的抗断能力接近,即拉伸温度为200 ℃下,峰值温度基本不影响抗断能力。而工况600 ℃~400 ℃下由于受到峰值温度和拉伸温度的双重影响,抗断能力与其他两个工况相比提高了66%;3)火灾后,试件的抗断能力均低于常温。其中螺栓暴露于峰值温度400 ℃再冷却后的抗断裂能力最差,损伤发展最快,其他工况(峰值温度200 ℃、600 ℃和800 ℃)的抗断裂能力接近,说明峰值温度400 ℃为一临界值,这是由于400 ℃处于螺栓制造时的回火温度区间(400 ℃~625 ℃),二次回火时,残留奥氏体分解而在结晶粒边界上析出碳化物,同时,杂质元素向晶界偏聚从而降低了晶界的断裂强度,导致出现回火脆化的趋势[28]。此外,高强螺栓作为特殊的高强钢,韧性较一般钢材更差,这些原因造成了 β值略高于一般钢材的经验取值范围,因此实际火灾中应对暴露于400 ℃并冷却后的螺栓节点予以重视。
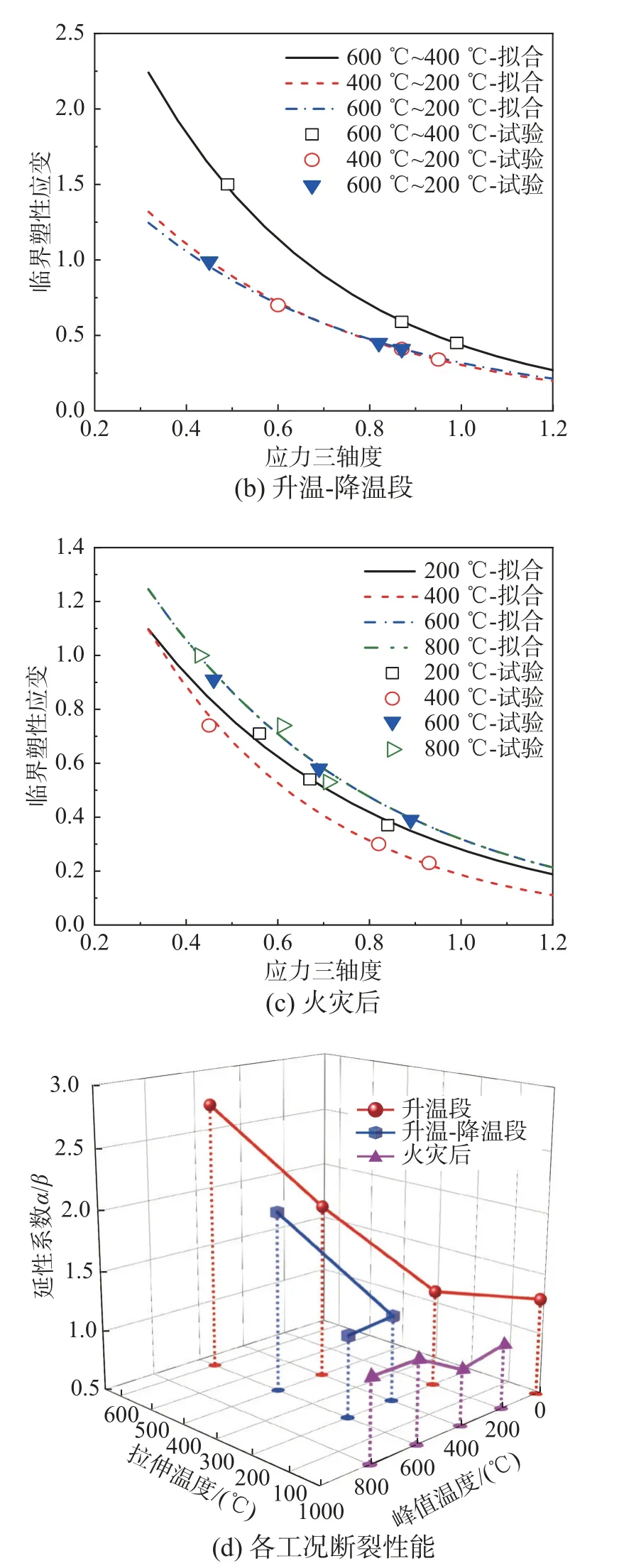
图7 火灾全过程SMCS 断裂模型及断裂性能Fig.7 SMCS fracture model and fracture performance in the whole process of fire
2.3 试验验证
将试验得到的真实应力-塑性应变曲线(图3)代入材料模型中,将拟合得到的SMCS 断裂模型(图7)引入如图8 所示的延性损伤准则中,拉伸应变率为0.001 s-1,满足GB/T228.1-2010 对准静态拉伸的要求。对拉伸断裂试件进行数值模拟,得到升温段、升温-降温段、火灾后试件的工程应力-应变曲线,分别如图9、图10、图11 所示。结果表明,断裂模型基本对试件颈缩前的应力状态没有影响;预测误差与试验类型、工况无明显关联,断裂时刻的应力、应变误差均小于12%,整体上模拟预测结果与试验吻合较好。
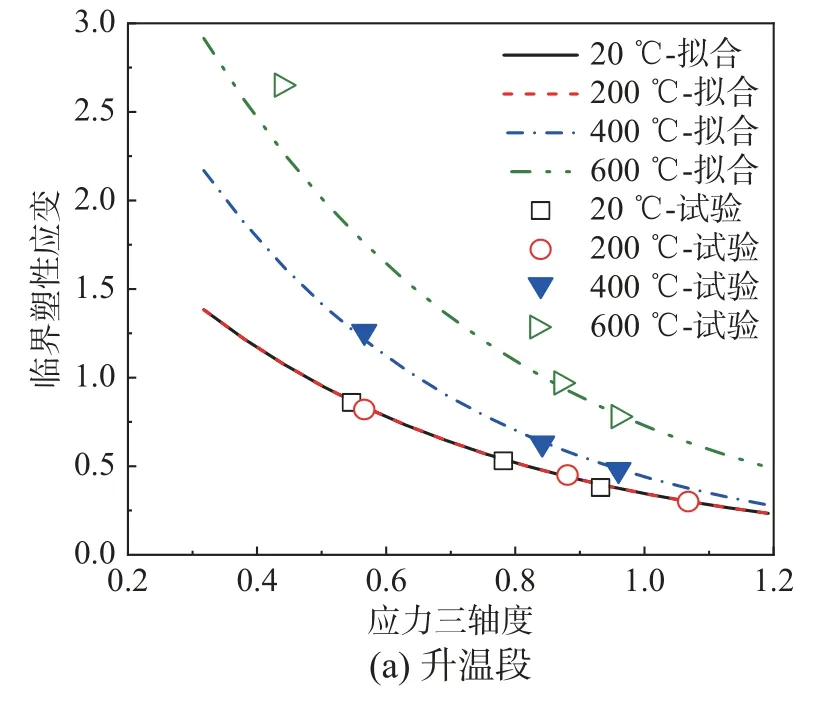
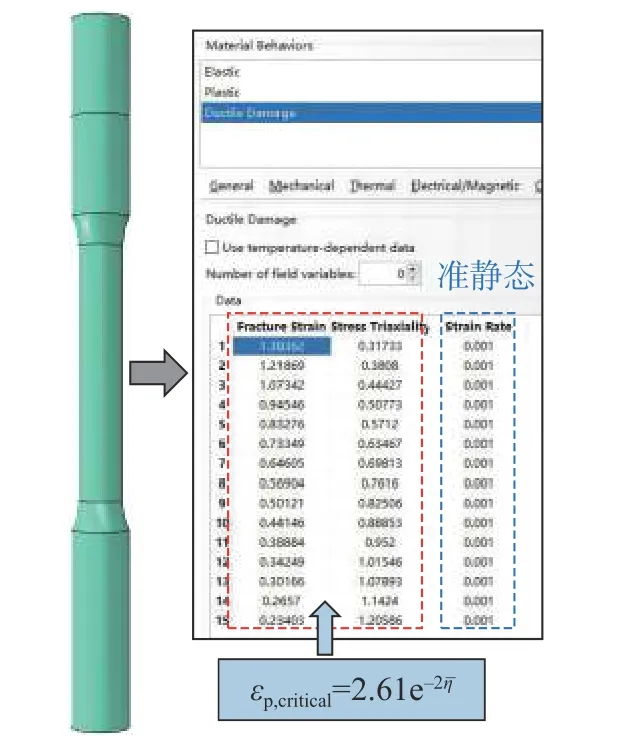
图8 ABAQUS 中定义SMCS 断裂模型Fig.8 Definition of SMCS fracture model in ABAQUS
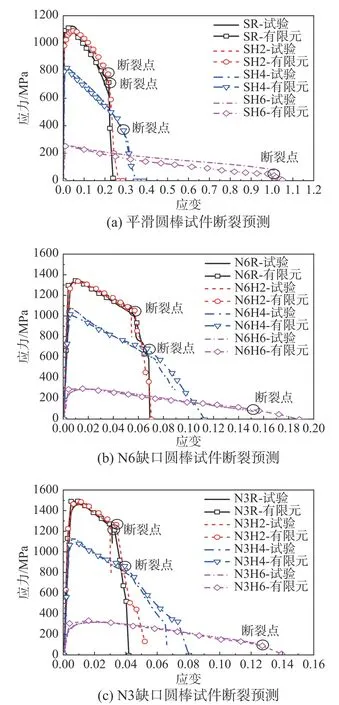
图9 升温段螺栓试件断裂过程对比Fig.9 Comparison of fracture process of bolt specimens in heating stage
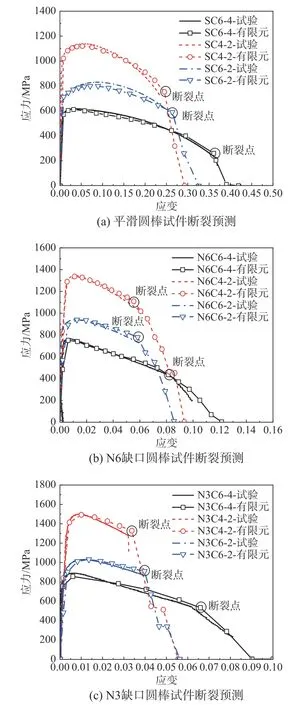
图10 升温-降温段螺栓试件断裂过程对比Fig.10 Comparison of fracture process of bolt specimens in heating-cooling stage
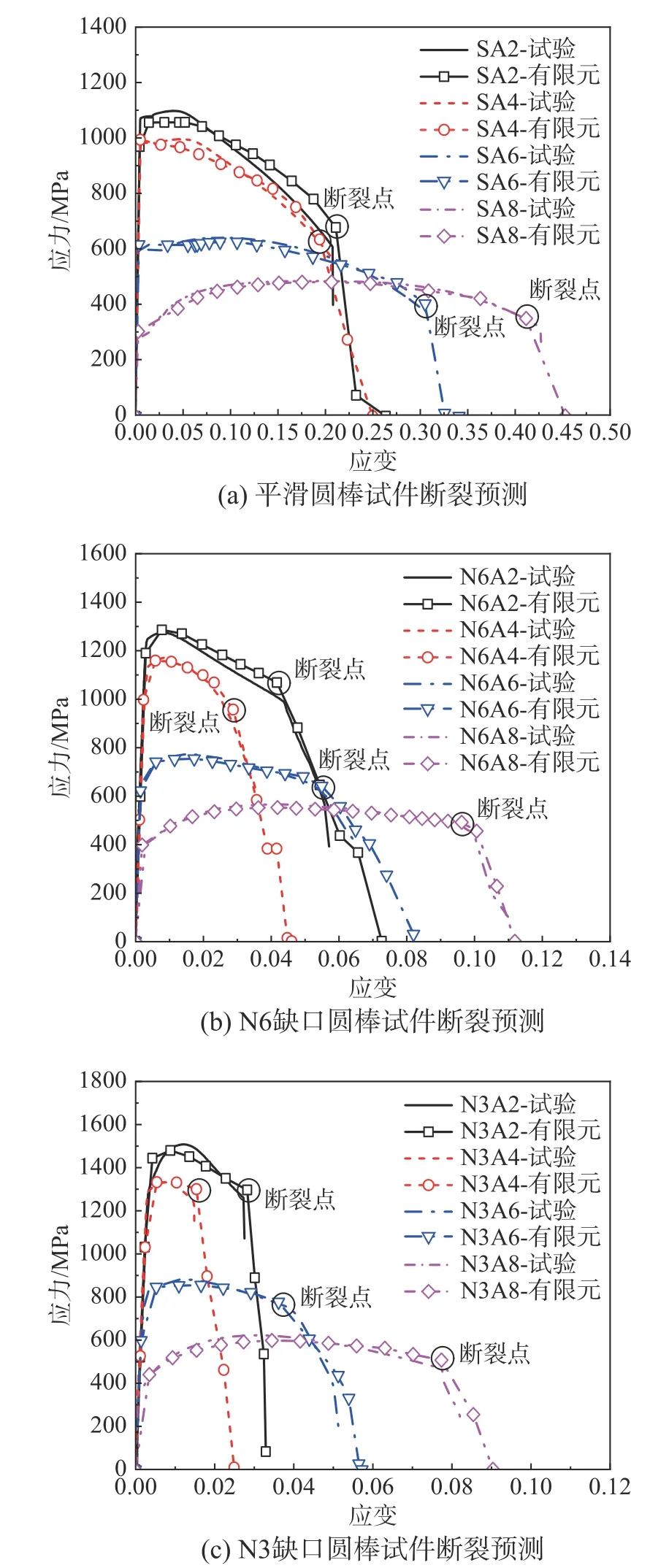
图11 火灾后螺栓试件断裂过程对比Fig.11 Comparison of fracture process of bolt specimens after fire
在图9(a)中,对于升温段600 ℃下的平滑圆棒试件(SH6),屈服后的应力模拟值与试验值差异较大,这是由于600 ℃下剧烈的高温软化造成的应力下降,600 ℃下的数值模拟偏保守;而N6H6和N3H6 试件缺口尺寸狭小,该影响较小。由于断裂起始点和终点与试验吻合较好,对应变的预测不造成影响。
3 T-stub 节点试验验证及参数分析
3.1 T-stub 节点高温破坏试验
BARATA 等[15]对T-stub 节点的高温断裂性能进行了试验研究,试验装置如图12 所示,试验采用稳态加载方法,将构件加热至目标温度(600 ℃)后保持温度恒定,对试件加载直至破坏。试验中,T-stub 节点只受轴向力,两螺栓处于受拉状态,与模型参数校准对应的拉伸试验中螺栓高应力三轴度状态一致,故本文选用该试验结果进一步验证SMCS 模型的适用性,并进行节点高温断裂行为的参数分析。
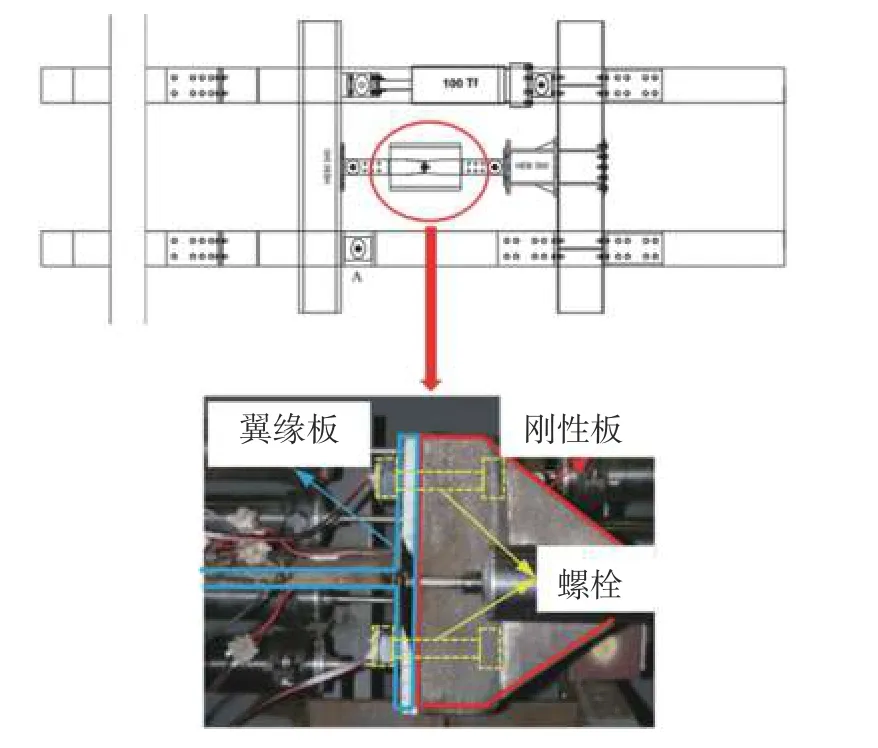
图12 T-stub 节点试验布置Fig.12 Set up of T-stub connection tests
试验中T-stub 节点试件包含翼缘板、刚性板和高强螺栓等组件,细部尺寸如图13 所示。其中,翼缘板和腹板均为S355 钢,弹性模量为206 GPa,屈服强度为385 MPa,极限强度为588 MPa。螺栓采用10.9 级高强螺栓(M24),试验中监测到各螺栓平均实际温度575 ℃。

图13 T-stub 节点组件细部尺寸 /mmFig.13 Detailed dimensions of T-stub connection components
3.2 T-stub 节点有限元模拟
在ABAQUS 中建立T-stub 节点有限元模型,如图14 所示,将翼缘板与腹板间的焊缝部位简化成一整体。刚性板的弹性模量和强度设置为远大于钢板和高强螺栓取值,不发生任何变形。螺栓杆(即断裂部位)网格尺寸需与2.2 节中单轴拉伸试件保持一致[29],T-stub 节点各组件网格划分见图15。

图14 T-stub 节点有限元模型Fig.14 Finite element models of T-stub connections

图15 T-stub 节点网格划分及边界条件Fig.15 Meshing and boundary conditions of T-stub
该试验在恒温600 ℃后拉伸,模拟中不考虑升温过程,认为整个构件均匀受热达到600 ℃,将节点各组件600 ℃下的基本力学材性和断裂模型直接输入到模型中。对于基本力学材性,翼缘板和腹板600 ℃下的弹性模量和强度折减按欧洲规范EC3[30]取值,10.9 级高强螺栓600 ℃下的材性按2.1 节拉伸试验结果取值(表3)。断裂模拟主要有2 类方法:① 极限塑性应变准则,不考虑应力三轴度的影响,在损伤准则中仅输入断裂应变,即极限塑性应变(常数),当等效塑性应变超过该常数值时判定材料进入起始损伤状态;② 考虑断裂应变随应力三轴度的变化,根据某种断裂模型确定两者的函数关系,对于本文的SMCS 模型,需同时输入几组断裂应变和应力三轴度,即图7 曲线中的关键点,当等效塑性应变位于曲线上方时判定材料进入起始损伤状态。本文中的损伤准则仅对损伤的起始进行预测,不考虑损伤演化过程。为了对比验证SMCS 断裂模型的准确性,对高强螺栓损伤准则进行4 种定义:① 不设置损伤准则,即假定螺栓可以无限拉伸不发生断裂;② 极限塑性应变准则,应变值依照EC3[30]不区分温度、钢材强度地取0.2~0.25;③ 极限塑性应变准则,应变值根据SEIF 等[31]对600 ℃的A490 螺栓标定值0.55;④ 输入2.3 节中校准的SMCS 断裂模型。S355 钢板600 ℃下延性损伤准则取文献[13]中试验获得的极限塑性应变0.3。
采用隐式静力分析模拟T-stub 节点变形全过程。边界条件为一端固结、一端施加位移荷载(图15(d)),荷载包括外荷载和螺栓预紧力。常温下,螺栓预紧力设计值与螺栓强度等级有关[32],按0.7 倍屈服强度对应荷载计算(接近施工预紧力大小),已有研究表明,常温下预紧力大小只影响T-stub 节点初始阶段,对塑性阶段发展和失效模式基本无影响[33];高温下,向征[34]假设预紧力受高温削弱程度与螺栓屈服强度一致,忽略预紧力随时间的变化。本文采用该假设施加高温下螺栓的预紧力。T-stub 模型中的接触类型为表面与表面接触,切向接触摩擦公式设置为罚,摩擦的方向性为各向同性,摩擦系数设置为0.2,不考虑摩擦系数受温度变化的影响;法向接触定义为“硬”接触,允许接触后分离。其中,对翼缘板与底部刚性板定义接触条件,可通过撬力作用使螺栓产生弯矩并发生明显的拉弯变形,但在判定失效时,仍以螺栓受拉侧单元达到临界值为失效条件(而不是整个螺栓)。
3.3 T-stub 节点试验验证
3.3.1 荷载-位移曲线验证
不同损伤准则下的荷载-位移曲线的数值模拟和试验结果对比如图16 所示。整体上,模拟得到的四条曲线在屈服(点A)前均与试验数据高度吻合,说明材料本构关系准确,建模有效。但是,点A之后的模拟值均略低于试验,误差主要来自实测平均温度略低于600 ℃,以及模型采用的材性与试验螺栓材料的差异。模拟得到的四条曲线在屈服前基本重合,说明T-stub 节点在屈服前的荷载-位移发展不受螺栓损伤准则的影响。
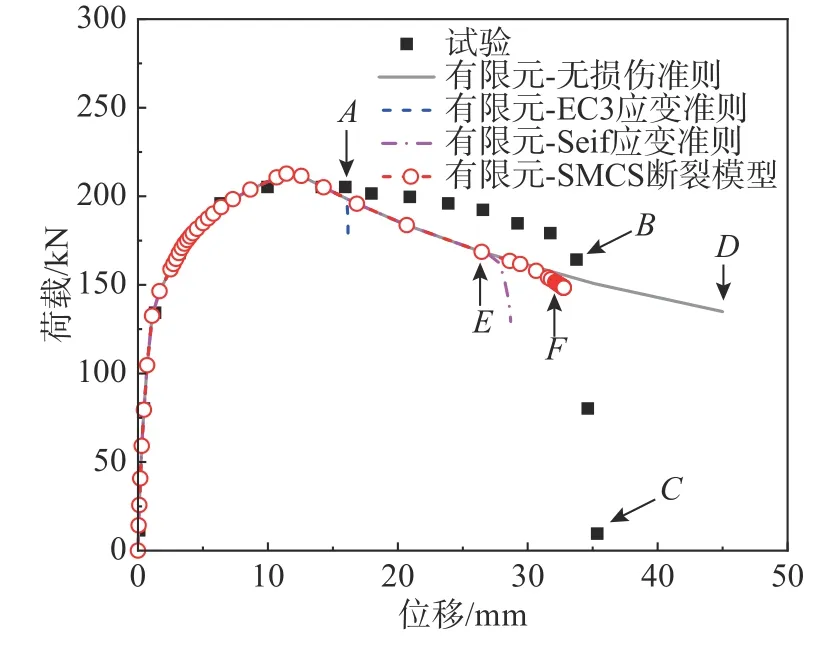
图16 不同损伤准则预测的节点荷载-位移曲线(600℃)Fig.16 Load-displacement curves of T- stub connection predicted based on different damage criteria (600℃)
如图16,试验中位移达到34.3 mm 时(点B)荷载骤降,直至点C荷载基本为0,试件完全失效。对于无损伤准则模型,节点屈服后应力继续发展到点D,位移达到45 mm 时荷载仍维持在125 kN,与实际情况不符,因此有必要对失效组件(高强螺栓)定义准确的损伤准则;当采用EC3推荐的极限塑性应变作为失效判定标准,在点A处位移为16.2 mm 时试件提前失效,断裂位移误差达52.7%;对于以Seif 标定的高强螺栓极限塑性应变值[31]作为失效判定标准的曲线,位移发展到点E时试件断裂(断裂位移为27.6 mm),误差降低为24.3%;采用本文校准的SMCS 断裂模型的曲线与试验值拟合最好,在点F处荷载出现突变(对应位移32.7 mm,荷载148 kN),断裂位移预测误差为4.7%。可见,不考虑应力三轴度的极限塑性应变准则对预测T-stub 构件高温断裂具有局限性,本文校准的考虑高应力三轴度的SMCS断裂模型对于预测T-stub 节点的高温受拉断裂行为具有更高的精度和更好的适用性。
3.3.2 失效模式验证
采用SMCS 断裂模型,600 ℃下数值模拟的失效模式与试验破坏结果对比如图17 所示,包括有限元模拟的等效塑性应变(PEEQ)和Mise 应力云图。结果表明,数值模型准确模拟出试件的高温破坏过程和失效模式,表现为翼缘板发生弯曲变形,随后两螺栓杆发生屈服、颈缩和断裂,失效模式为螺栓杆发生大变形而断裂失效。

图17 失效模式数值模拟与试验结果对比Fig.17 Comparison of failure modes from numerical simulation and tests
3.4 T-stub 节点断裂性能参数分析
本节采用经过试验验证的有限元模型进行参数分析,进一步研究T-stub 节点在火灾全过程中的断裂行为,研究温度历程对T-stub 构件的失效模式、承载能力和延性的影响。考虑更广泛的温度范围:增加火灾升温段拉伸温度为20 ℃、200 ℃、400 ℃工况;增加三种升温-降温段工况,即600 ℃~400 ℃、400 ℃~200 ℃、600 ℃~200 ℃;增加火灾后峰值温度为200 ℃、400 ℃、600 ℃、800 ℃四种工况。其中,S355 钢火灾全过程损伤准则采用文献取值(考虑应力三轴度),高强螺栓损伤准则采用2.3 节校准的SMCS 模型。
3.4.1 T-stub 节点失效模式
不同温度工况下T-stub 节点失效模式主要有三种,如图18 所示。火灾升温段,温度低于200 ℃时,在螺栓屈服前,栓孔附近和腹板焊趾处的翼缘板率先屈服并出现塑性铰,随后断裂,导致T-stub构件失效,属于模式1(翼缘板屈服断裂)。此时螺栓变形远小于翼缘板,且螺栓强度未被充分利用;火灾升温段温度达到400 ℃时,螺栓和翼缘板几乎同时发生明显变形,腹板焊趾处的翼缘板屈服并出现塑性铰,同时螺栓受拉屈服断裂,螺栓强度得到充分利用,属于模式2(翼缘板和螺栓同时屈服断裂);温度升高至600 ℃时,由于高强螺栓的延性较常温有大幅度提高(约3.5 倍),螺栓杆相对翼缘板发生明显变形,而600 ℃以上高强螺栓的力学指标衰退程度(表2)较普通钢更大更快,因此翼缘板的强度和刚度相较螺栓更强,螺栓首先发生断裂破坏,属于模式3(螺栓屈服断裂),高强螺栓成为影响整个T-stub 节点变形的决定性因素。其他温度工况下节点失效模式在表5中列出,对于升温-降温段和火灾后工况,节点表现出模式1 和模式2 的失效模式,随着温度升高,节点失效模式由模式1 向模式2 转变。

图18 T-stub 节点失效模式Fig.18 Failure modes of T-stub connections

表5 火灾全过程下T-stub 节点断裂行为指标Table 5 Fracture behavior of T-stub connections in the whole process of fire
3.4.2 T-stub 节点火灾全过程受力性能
参数分析得到的节点火灾全过程荷载-位移曲线如图19 所示。曲线峰值点对应的纵坐标为极限承载力,横坐标为极限位移,不同温度工况数值模拟结果列于表4,其中延性系数定义为某温度下节点极限位移与常温下节点极限位移(19.65 mm)的比值,用于评估火灾全过程下T-stub 节点的变形能力。

图19 火灾全过程下T-stub 节点荷载-位移曲线Fig.19 Load-displacement curves of T-stub connections in the whole process of fire
图20 显示了拉伸温度、峰值温度和延性系数三者之间的关系。节点的变形能力(即延性系数)与失效模式有关。不同的失效模式本质上是由于翼缘板和螺栓的塑性发展不同步。当材料起裂点应力三轴度越大,应力约束程度越高,临界塑性应变呈指数形式下降,塑性发展过程越短,因此应力三轴度只影响荷载-位移曲线极限位移。失效模式1 发生在温度较低的工况(峰值温度或拉伸温度低于400 ℃)的工况,这些工况下撬力作用较大,翼缘板的应力三轴度发展较快,先于螺栓达到临界塑性应变翼缘板比螺栓先发生断裂,构件的变形能力取决于翼缘板,基本保持在常温水平,即延性系数在1.0 左右;对于失效模式2 的工况,翼缘板和螺栓的应力三轴度同时发展,几乎同时达到各自临界塑性应变,缩短了塑性发展过程,翼缘板屈服伴随螺栓屈服断裂,节点整体变形比模式1 小,延性系数在0.63~0.72 范围内;所有工况中,仅在升温段600 ℃下发生失效模式3,翼缘板不完全屈服,且强度和刚度较高强螺栓更大,由于撬力几乎为0,翼缘板和螺栓的应力三轴度发展缓慢且接近初始状态,晚于前两种模式达到临界塑性应变,T-stub 节点的延性主要由高强螺栓控制,同时延性系数提高到1.67。
3.4.3 预紧力的影响
以火灾升温段600 ℃试验为例,对T-stub 模型中的螺栓分别施加大小为0、0.35fu,600As、0.7fu,600As、fu,600As的预紧力。图21 表明,预紧力取值大小对其影响是有限的,火灾过程中预应力无论损失程度多大,均只对初始刚度造成影响,因此高温造成的预紧力损失程度对本研究结果影响很小。
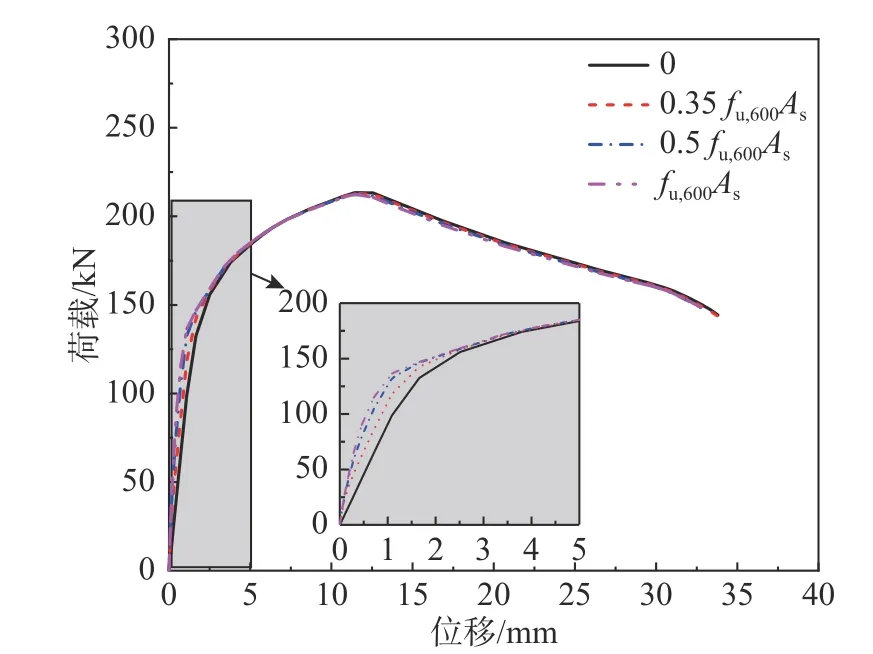
图21 预紧力对T-stub 节点的影响Fig.21 Influence of preloading on T-stub connection
4 结论
本文基于螺栓拉伸断裂试验结果,校准了10.9 级高强螺栓火灾全过程下(升温段、升温-降温段、火灾后)高应力三轴度对应的SMCS 断裂模型,并应用于T-stub 节点高温受拉断裂行为预测,研究不同损伤准则和温度历程对节点失效模式的影响。得到以下结论:
(1) SMCS 模型可以有效预测火灾全过程和高应力三轴度(0.3~1.2)下10.9 级高强螺栓的断裂行为,断裂应力和断裂应变预测误差均小于12%。相比于采用常数极限应变的极限塑性应变准则,SMCS 模型对于预测T-stub 节点高温断裂性能具有更好的精度。
(2) 拉伸温度和峰值温度是影响高强螺栓抗断能力的主要因素。升温段,温度高于400 ℃时,抗断能力随温度线性增长,600 ℃时抗断能力为常温值的2 倍;降温段,600 ℃降至400 ℃拉伸时螺栓抗断能力可提高60%,拉伸温度为200 ℃时受峰值温度影响较小;火灾后螺栓抗断能力较常温更弱。
(3) 不同温度历程下T-stub 节点主要有3 种失效模式:翼缘板屈服断裂(模式1)、翼缘板和螺栓同时屈服断裂(模式2)、螺栓屈服断裂(模式3)。随着温度升高,节点失效破坏由模式1 向模式3转变。
(4) T-stub 节点的变形能力(延性系数)与失效模式有关。失效模式1 发生在峰值温度或拉伸温度低于400 ℃的工况,节点延性系数在1.0 左右变化;节点发生失效模式2 的变形能力较模式1更小,极限位移为常温值的63%~72%;在升温段600 ℃时发生失效模式3,节点变形能力提高到常温值的1.67 倍。

