考虑场址危险一致性的中国完备条件目标谱与记录选取

汪维依，冀 昆，温瑞智，任叶飞

(1.中国地震局工程力学研究所中国地震局地震工程与工程振动重点实验室，黑龙江，哈尔滨 150080；2.地震灾害防治应急管理部重点实验室，黑龙江，哈尔滨 150080；3.河海大学土木与交通学院，江苏，南京 210024)

随着结构弹塑性时程分析越发普遍，如何选取合适的地震动输入进行结构抗震分析受到越来越多的关注。在相同的抗震设防烈度与场地条件下，《建筑抗震设计规范》[1]给出的目标谱是基本一致的。但不同地区、不同场址所处的具体地震地质构造环境与地震活动性水平都存在较大差异，仅仅依据抗震设计规范给出的峰值加速度和设计目标谱确定地震动输入是不够的。除了考虑目标结构特性之外，合理的地震动输入应保证所选地震动与目标场址的概率地震危险性分析(Probabilistic seismic hazard analysis, PSHA)的结果相匹配。也就是说，地震动输入是基于概率地震危险性水平而不是地震动强度指标(Intensity measures, IM)来确定。一旦工程结构和所在场址确定，结构响应指标的年超越概率曲线是不受地震动输入选择影响的。要实现这一点，就要保证地震动输入尽可能“真实”地反映当地可能遭受地震的“危险性水平”。这样可以极大降低地震动输入不确定性造成的响应结果差异，这就是危险一致地震动输入的核心思想[2]。确定危险一致地震动的一般思路是：概率地震危险性分析—危险一致目标谱—记录匹配—确定地震动输入。可以看到，危险一致地震动输入的核心环节是目标谱的构建与记录匹配。

一致概率谱(Uniform hazard spectrum, UHS)本质上就是最早基于危险一致思想构造的目标谱，在国内外得到了广泛应用，比如我国重大工程的地震安全性评价中就以UHS 为地震动输入的目标谱[3]。其构建思路是，确定目标地震危险性水平下不同周期点的IM(如加速度反应谱值Sa等)，得到整体谱型具有相同超越概率的目标谱。UHS 具有三个理论缺陷：① UHS 的各个周期点的Sa值都是单独通过PSHA 确定的，彼此相互独立，但实际上某条天然地震动的反应谱不可能在所有周期下都有一致的超越概率；② UHS 无法找到对应的唯一的设定地震，因为不同Sa的最大贡献设定地震事件并不相同；③ UHS 仅考虑了均值，没有给出记录间离散性的定义[4]。用UHS 作为目标反应谱选择地震动用于结构的非线性动力分析，结果偏大。针对缺陷1 和缺陷2，BAKER和ALLIN[5]提出了条件均值谱(Conditional mean spectrum, CMS)的概念。CMS 以目标周期T*(一般选择结构的基本振动周期)下的谱加速度Sa(T*)作为目标值，借助Sa的地震动预测方程和Sa相关系数矩阵确定其余周期点Sa在Sa(T*)条件下的取值。如果通过条件高斯分布将条件离散性也考虑进去，得到的结果为条件谱(Conditional spectrum)[6-7]。计算时，若使用平均或者最大贡献设定地震和单一地震动预测方程，这样得到的条件谱称之为粗略条件谱。若将PSHA 过程中涉及的多个设定地震事件与不同地震动预测方程的逻辑树权重都考虑进去，则称之为完备条件谱。针对粗略条件谱我国近年来也有了较多研究成果，如韩建平等[8]针对CMS 对不同结构响应的离散性控制以及谱型参数在易损性分析的作用进行了研究；吕大刚等[9-10]衔接西安市地震危险性分析结果进行了CMS 构建；以及冀昆等[11-12]提出针对重大工程地震安全性评价产出的狭义CMS/CS 构建流程。但是上述研究主要针对粗略条件谱，关于完备条件谱的研究尚未充分开展。在作者的前期研究中，采用我国五代区划图相同的潜源分布与地震动衰减关系，进行了中国主要城市的危险性分析与设定地震解耦[13]，为本文计算完备条件谱提供了基础。

除了构建危险一致目标谱外，另一个需要考虑的问题就是，如何实现强震动记录与目标谱的匹配。对于服从多元高斯分布的“粗略”条件谱，可以通过拉丁超立方抽样方法等手段实现，由均值和协方差矩阵得到服从目标分布的模拟反应谱，进而逐一匹配模拟谱实现记录的选取。借助贪心优化算法等思路[14]，可实现对CS 目标均值与标准差的高效匹配。但是，对于完备条件谱来说，其不再满足多元高斯分布，由于无法定义高斯混合分布的协方差矩阵，只能采用两步蒙特卡罗抽样的思路生成模拟谱，进而采用假设检验直接对Sa指标的累积概率分布是否“接近”目标分布作为记录选取依据[15]。这种记录选取方法虽然保证了Sa指标分布与目标分布接近，但是实践中发现无法保证工程更感兴趣的均值与标准差的较好匹配，而且过程较为繁琐[13]，需要生成数百条模拟谱才可以保证与完备条件谱的理论分布接近。由于我国的条件谱在构建过程中并不存在多个衰减关系逻辑加权，高斯混合分布的协方差矩阵理论上和多元高斯分布之间差异性有限。如果将高斯混合分布的协方差矩阵进行近似，那么就可以采用粗略条件谱的匹配思路进行记录选取，本文将提出适用于我国完备条件谱的记录匹配思路。

本文利用前期研究中给出的我国主要城市的地震概率危险性分析结果，分别给出了基于二维设定地震解耦结果的“粗略”条件谱，和基于三维设定地震结果的完备条件谱。之后以北京近郊某城市为例，进行了两种条件谱的对比讨论，探讨了加速度反应谱相关系数对条件谱的影响，最后给出了适用于我国完备条件谱的高效记录匹配方法。基于完备条件谱选取的地震动记录与场址的地震危险性一致，可服务于新一代的基于性态的地震工程(performance-based earthquake engineering,PBEE)[16]中的结构需求指标概率危险性计算[17]。作为全概率PBEE 方法中连接概率地震危险性分析和结构易损性分析[18-19]的桥梁，基于完备条件谱选取地震动输入有着承上启下的作用。

1 完备条件谱构建方法

1.1 衔接我国五代区划图的设定地震解耦

笔者在前期工作[13]中，采用与我国五代地震参数区划图一致的地震动三级潜源划分与衰减关系，在OpenQuake[20]平台上进行了中国大陆的地震概率危险性分析，进一步给出了各个主要城市的设定地震解耦结果。对于中国大陆的34 个主要城市，研究得到的峰值地面加速度值基本位于第五代地震危险图给出的区间范围内，验证了结果与我国现行地震动参数区划图[21]是基本一致的。同时给出了平均重现期为475 年和2475 年的Pga和Sa值在周期为0.2 s、0.3 s、0.5 s、0.7 s、1.0 s、1.5 s 和2.0 s 时的超越概率曲线和设定地震解耦结果(https://github.com/JIKUN1990/China-Seismic-Haz ard-Deaggregation-34cities)。后文将要用到的北京近郊某城市的二维(震级-距离)设定地震解耦和三维(震级-经纬度)解耦结果如图1 所示。图中方柱的不同高度代表重现期为2475 年周期为1.0 s 下各个设定地震事件微元的贡献率，其中，图1(a)中的方柱表示的是每个震级-距离微元的贡献率，图1(b)中不同边框线型的方柱表示的是该城市研究区域内(120 km 内)的各个潜源中不同经纬度栅格点在各震级下的贡献率。

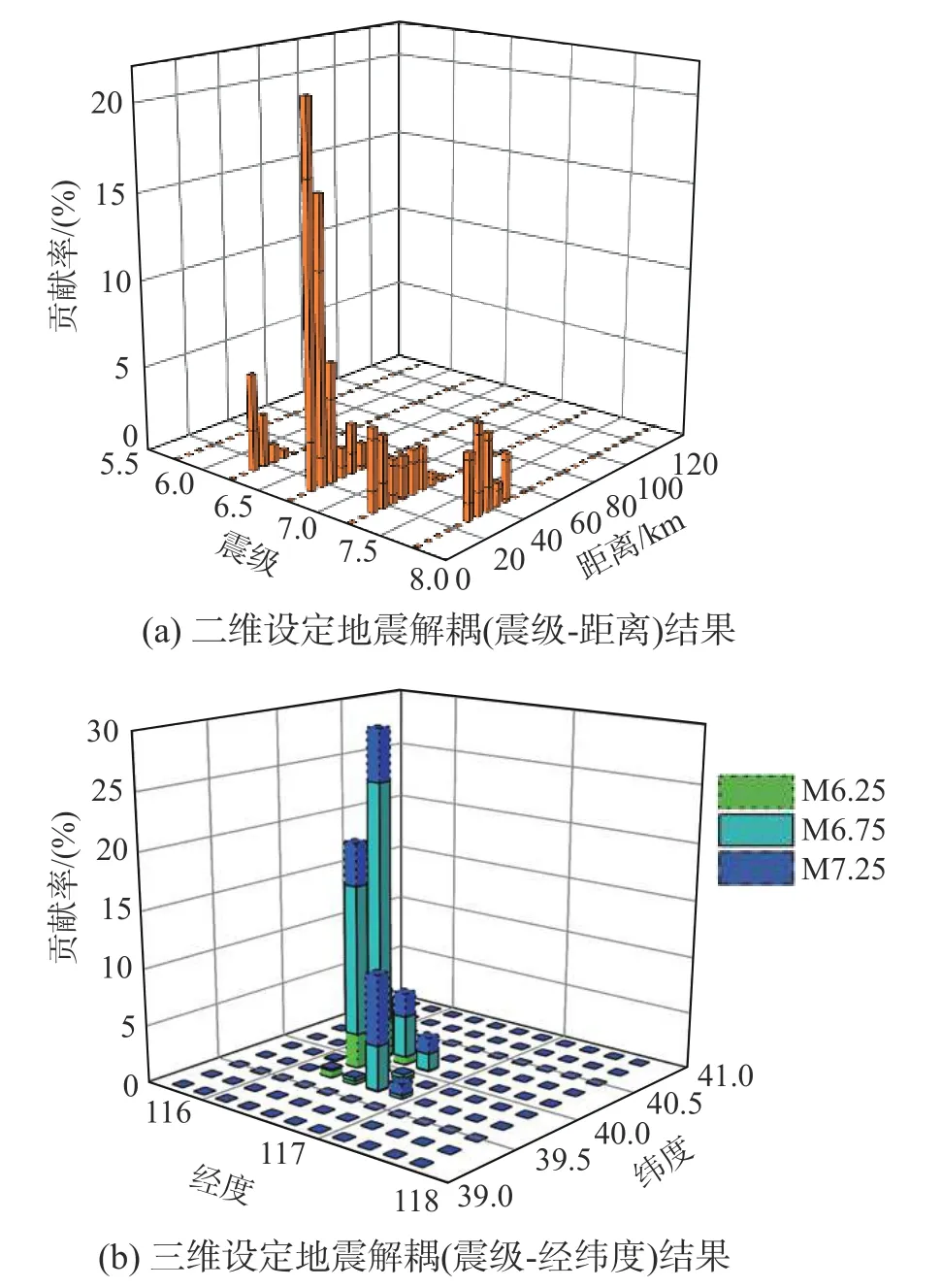
图1 重现期2475 年下周期1.0 s 的设定地震解耦结果Fig.1 Disaggregation of earthquakes with a period of 1.0 s under the return period of 2475 years

1.2 粗略与完备条件目标谱构建

1) 衔接二维设定地震的粗略条件目标谱构建

首先，在给定危险性水平下，基于二维设定地震解耦结果得到不同震级-距离(M,R)地震事件的贡献率。通过对贡献率进行加权平均或者采用最大贡献率可以得到单个具有代表性的设定地震事件(M,R)，基于这个设定地震事件来构建的条件目标谱就是“粗略”条件谱。假设这里的目标地震动强度指标为周期T*处的谱加速度，Sa(T*)。使用谱加速度的地震动衰减关系获得Sa在所有周期Ti的对数平均值和标准差，表示为μlnSa(M,R,Ti)和σlnSa(M,R,Ti)。我国地震区划图采用的地震动衰减关系[22]包括长轴衰减关系和短轴衰减关系，计算的粗略条件谱包括长轴和短轴的计算结果。对于目标谱加速度值Sa(T*)，计算其与目标周期T*处μlnSa(M,R,Ti)的差值ε(T*)。

依据条件概率公式，得到任意周期Ti处的粗略条件反应谱的谱加速度对数值的条件均值μlnSa(Ti)|lnSa(T*)为：

式中：μlnSa(M,R,Ti)和σlnSa(M,R,Ti)为衰减关系给出的周期点Ti的对数均值和对数标准差；ρ(Ti,T*)为两个周期点Sa值的皮尔逊相关系数，该系数一般利用强震动记录数据库进行统计得到。

任意周期Ti处的粗略条件反应谱的谱加速度对数值的条件标准差σlnSa(Ti)|lnSa(T*)为：

在给定设定地震的情况下，多个周期的对数谱加速度值服从多元高斯分布[23]，该分布可通过lnSa值的均值和协方差矩阵确定，协方差矩阵为：

式中：ΣTi,Tj=ρ(Ti,Tj)σlnSa(Ti)σlnSa(Tj)为lnSa在周期Ti和周期Tj间的协方差；p为所计算的周期的个数。条件谱是在给定条件周期T*处谱加速度值下的对数谱加速度值的概率分布，可通过条件均值和条件协方差矩阵来表达，条件均值由式(2)给出，条件协方差矩阵可通过式(5)得出：

式中：Σcross是p×1的向量，表示lnSa在周期Ti和条件周期T*间的协方差，Σcross=[ΣT1,T*ΣT2,T*··· ΣTp,T*]。

2) 衔接三维设定地震的完备条件目标谱构建

在我国第五代地震参数区划图中，为了考虑断层走向的影响，定义了方向性函数来表示不同轴向的概率(如图2 所示)，结合俞言祥等[22]给出的长短轴衰减关系进行地震动参数计算。三维设定地震解耦结果描述了不同震级-经纬度微元对目标危险性水平的贡献概率。如果对每一个震级-经纬度微元都进行条件谱的构建，然后，将所在潜源的方向性函数作为概率进行加权组合，最后，通过高斯混合分布就可以得到考虑所有潜源贡献与方向性概率的完备条件谱。

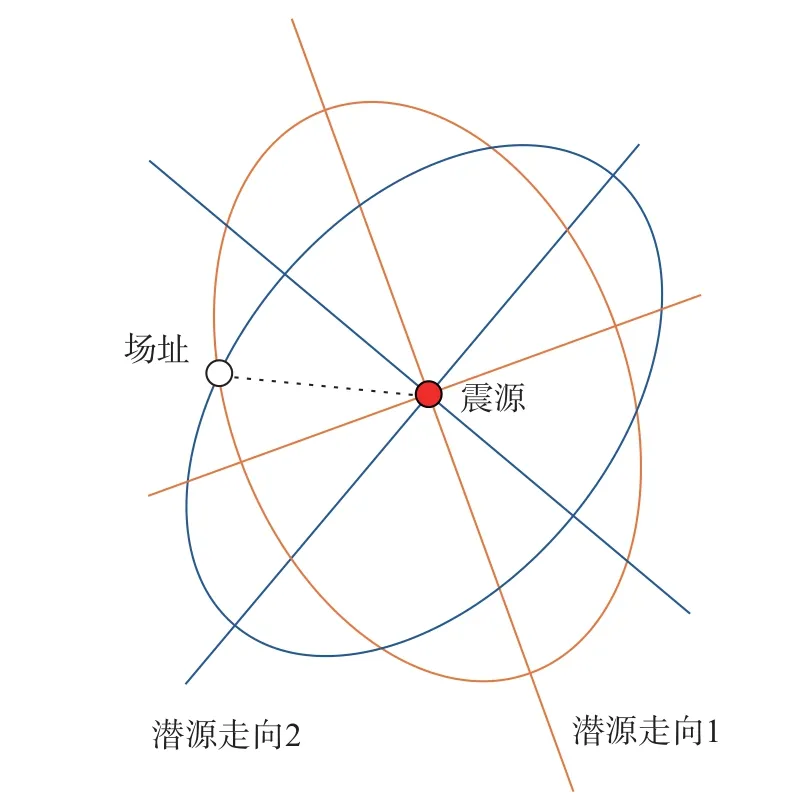
图2 潜源走向示意图Fig.2 Schematic diagram of strike directions of the source area

在目标危险性水平下，假设三维设定地震解耦得到的微元k的贡献率为Pk，该值基于三维设定地震解耦给出。则通过与微元所在潜源走向的概率相乘，即可得到微元k在走向s上的概率，记作Pk,s。将震级、距离和方位角代入俞言祥的长短轴衰减关系[22]后，则该微元k在走向s下的条件均值μlnSa(Ti)|lnSa(T*),k,s和条件标准差σlnSa(Ti)|lnSa(T*),k,s定义如下：

微元k在各走向s下的条件均值和条件标准差均服从高斯分布(正态分布)，且微元k在各走向s下具有相同的条件标准差：

那么考虑了各个潜源的可能方向后，微元k的条件均值μlnSa(Ti)|lnSa(T*),k和条件标准差σlnSa(Ti)|lnSa(T*),k为：

最后，将所有设定地震微元的条件均值和标准差进行相加后就得到了考虑所有设定地震微元与可能方向性贡献的完备条件谱，其均值和标准差为：

由于完备条件谱依据高斯混合分布构建，协方差矩阵并没有解析表达。

1.3 案例城市条件目标谱构建实例

衔接图2 的二维和三维解耦设定地震解耦结果，采用1.2 节中介绍的构建方法，分别构建50 年超越概率2%下条件周期T*=1.0 s 的粗略条件谱和完备条件谱。其中粗略条件谱分别采用了俞言祥等[22]衰减关系长轴，短轴，以及长短轴平均值三种方式计算。对比粗略条件谱与完备条件谱的条件均值和对数标准差如图3(a)和图3(b)所示。

图3 50 年超越概率2%下，条件周期为1.0 s 的条件谱Fig.3 Condition spectrum with conditional period of 1.0 s under the 50-year excess probability of 2%

从图3(a)可以看到，完备条件谱的均值介于使用长短轴衰减关系的粗略条件谱的结果之间。图3(a)的均值谱对比结果表明，就案例城市而言，采用衰减关系长短轴几何平均值构建的粗略条件谱，相较单独采用长轴或者短轴的结果要更接近完备条件谱。由于完备条件谱考虑了目标场址周围潜源所有栅格点的贡献，而不是单一设定地震，所以其包含了更多潜源信息。但是由于本案例城市的设定地震并不是二极分布类型(即在远场和近场均存在影响较大的控制潜源或设定地震事件)，所以采用加权平均贡献设定地震事件得到的粗略条件谱与完备谱基本一致。在进行震级-经纬度三维设定地震解耦比较困难，或者其他构建完备条件谱存在障碍的情况下，可以直接采用这种近似方式来估计条件目标谱的均值。图3(b)的标准差对比结果表明，完备条件谱的条件标准差要大于粗略条件谱。从式(12)也可以看出，完备条件谱的条件标准差除了包含与粗略条件谱一样的条件标准差外，还包含了潜源走向不确定性带来的离散性。值得指出的是，本研究仅考虑了潜源走向的不确定性，当不止一个地震动预测方程通过逻辑树权重参与了PSHA 计算时，则预测方程的权重需要在高斯混合分布中一并考虑进去。

2 加速度谱相关系数矩阵的区域性影响分析

在上述目标谱构建的过程中的相关系数ρ(Ti,T*)采用了BAKER 和JAYARAM[23]提出的BJ08 模型，此相关模型基于美国西部下一代衰减关系项目(Next Generation Attenuation-west Project, NGAwest)数据库和衰减关系拟合得到，周期范围为0.01 s～10.0 s。有学者基于不同的数据集来验证BJ08相关模型在不同地区的适用性：① JAYARAM等[24]针对日本台网的记录(包括俯冲带地震)；② CIMELLARO[25]使用来自欧洲地震数据库的记录；③ DANESHVAR 等[26]使用北美东部的典型记录；④ JI 等[27]选用了来自中国2007 年-2014 年的强震动记录数据集，震级从MS5.5 到MS7.0，震中距小于200 km。

图4 比较了JI 等[27]基于中国2007 年-2014 年地震记录集的获得相关系数，基于NGA-west1数据集的BJ08 相关系数，以及基于NGA-west2 数据集拟合的相关系数结果。

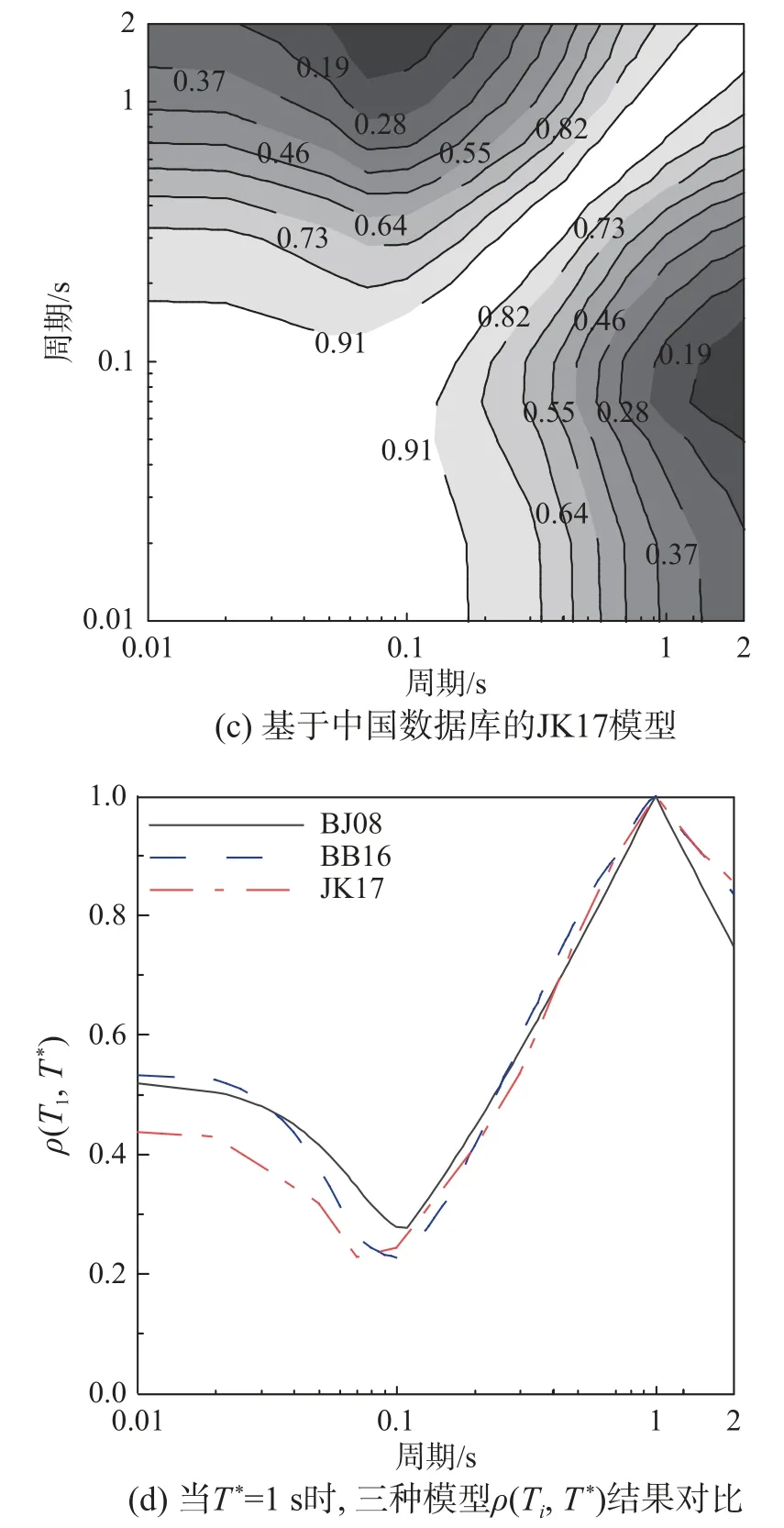
图4 相关系数对比Fig.4 Comparison of correlation coefficients

比较图4 中的相关系数结果可知，BAKER等[28]基于NGA-West2 拟合的相关系数结果、JI 等[27]基于中国记录拟合的相关系数结果和BJ08 相关系数模型趋势基本一致。当Ti接近Tj时，相关系数ρ(Ti,Tj)接近1；当Ti远离Tj时，相关系数ρ(Ti,Tj)减小。

为了进一步比较这些结果，图4(d)给出了条件周期T*=1.0 s 时，基于BJ08、BB16 和JK17 模型预测得到的反应谱相关系数ρ(Ti,T*)。可以看到，相关系数曲线形状是基本一致的，尤其是在0.1 s～2.0 s 之间，但是在相关系数较低的0.01 s～0.1 s 之间，基于中国数据拟合得到的JK17 模型下的相关系数值是显著低于其余两个模型的。以本研究的算例城市为例，分别建立了基于三种不同相关系数模型的条件周期为1.0 s 的完备条件谱和粗略条件谱，其条件均值和对数标准差对比结果见图5 和图6。其中粗略条件谱包括基于衰减关系长轴、短轴，以及二者几何平均值三种目标谱。可以看到，三种相关系数下的完备条件谱、粗略条件谱的条件均值以及条件标准差具有一致的变化趋势。但是基于我国JK17 模型得到的目标谱在0.5 s 附近区段是高于其他相关系数模型的结果的，条件标准差结果反而要低于其他模型。当选取记录数据集完全来自中国强震记录数据库时，相关系数模型的这一差异是需要考虑的，建议采用基于中国数据拟合的JK17 模型体现中国区域的地震动特征。

图5 三种相关系数下周期0 s～2 s 条件均值对比Fig.5 Condition mean spectrum of 0 s～2 s under three kinds of correlation coefficients

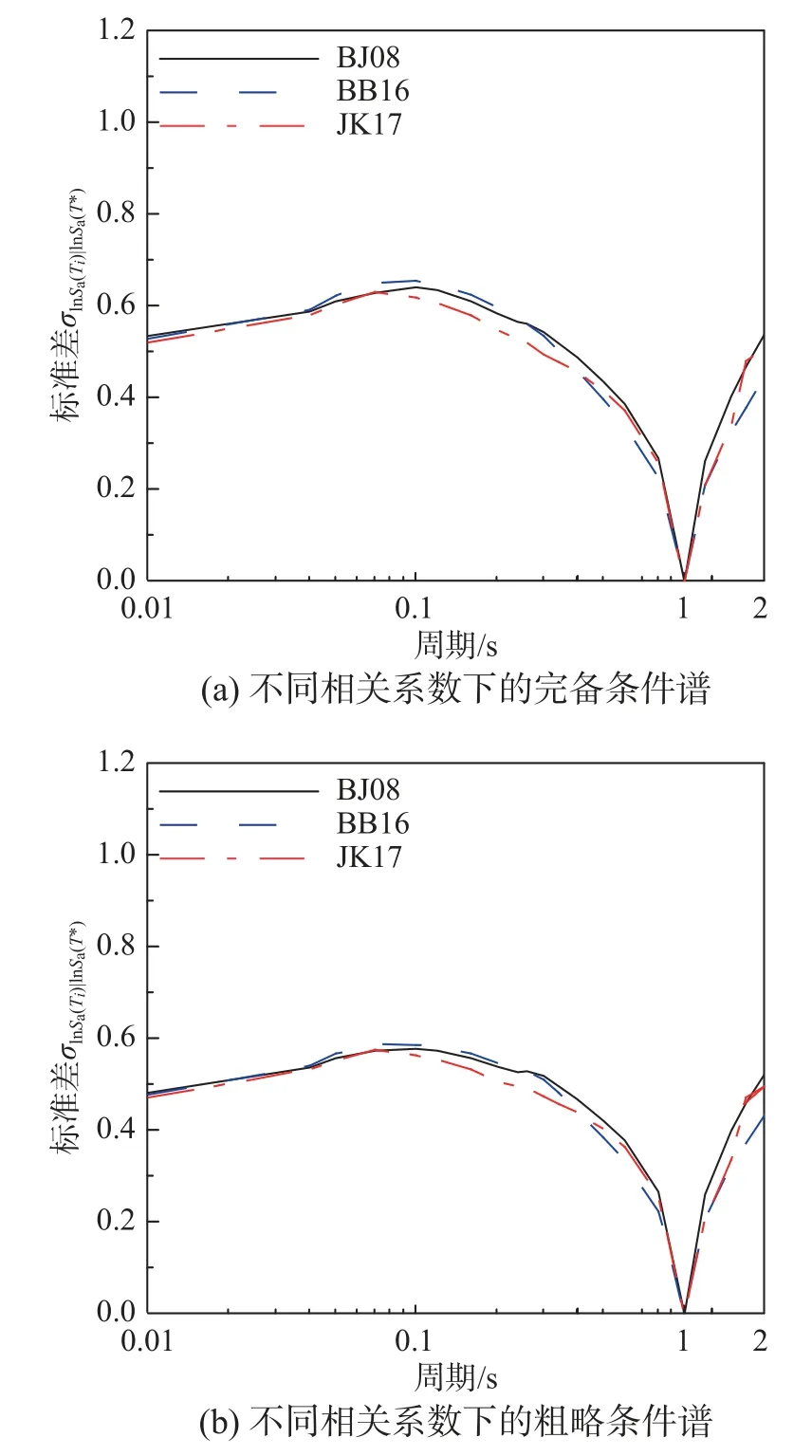
图6 三种相关系数下周期0 s～2 s 标准差对比Fig.6 Standard deviation of 0 s～2 s under three kinds of correlation coefficients

3 面向完备条件谱的记录选取方案

和单纯的匹配条件目标谱的均值不同，同时匹配目标条件谱分布是一个多维优化问题，即从一个大的记录数据库中搜寻N条记录，使其地震动强度指标(Sa)的分布情况与目标分布一致。对于粗略条件谱来说，其严格满足多元高斯分布，且均值、协方差矩阵都有直接的数学解析表达，因此可以通过拉丁超立方抽样方法直接得到符合分布的模拟谱。进而通过逐一匹配模拟谱实现最终的记录选取，采用贪心优化的思路逐一替换模拟谱记录搜寻具有较好匹配效果的记录[14]，记录匹配的思路见图7 的流程图。但是作为完备条件谱，其采用了高斯混合分布构造，综合考虑了目标场址所有潜源设定地震事件的权重，虽然条件均值和条件标准差可以求出解析表达，但是无法直接计算得出协方差矩阵，因而无法直接通过拉丁超立方抽样得到与选波数量相同的模拟谱作为目标来匹配。

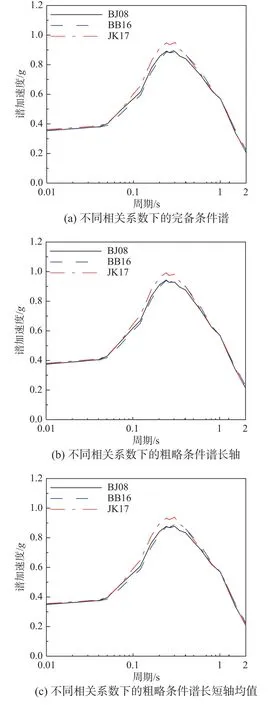
图7 服从高斯混合分布的完备条件谱的天然地震动记录选取流程Fig.7 Flow diagram of ground motion selection of exact conditional target spectrum obeying gaussian mixture distribution

BRADLEY[29-30]提出通过两步蒙特卡罗抽样的方式来获得模拟谱：首先，通过潜源微元贡献率进行蒙特卡罗抽样得到随机的潜源微元；然后，计算得到随机潜源微元下的条件谱作为模拟谱。这样做虽然可以得到满足完备条件谱高斯混合分布的结果，但是存在以下弊端：① 由于采用的是蒙特卡罗模拟技术，模拟谱的数量一般需要远超最终在后续时程分析中用的记录数量，才可以保证模拟谱的均值与标准差与目标分布一致。由图8的不同工况下的对比算例可以看到，采用模拟谱的均值和方差与模拟反应谱的条数有很大的关系。当模拟次数达到100 或者更多时，才能得到与目标谱的均值和标准差一致的一组模拟反应谱。同时，由于其基于三维设定地震解耦结果进行模拟谱的构建，当潜源出现二极类型(即近场和远场同时存在贡献率较大的设定地震事件)时，会导致模拟谱出现较大偏差，可能出现谱型截然不同的两簇模拟谱。② 由于记录选取时并非逐条匹配模拟谱，而是通过匹配地震动强度指标的累积概率分布曲线，因此无法很好地控制最后选取结果的均值和标准差[13]，这会影响后续结构响应的计算结果。

图8 随机模拟方法生成不同数量模拟反应谱的均值及标准差Fig.8 Mean and standard deviation of different numbers of simulated response spectra generated by stochastic simulation method

考虑到中国完备条件谱在构建过程中并不涉及多个衰减关系的逻辑权重，且采用的衰减关系本身形式较为简单，本研究提出一种简化的匹配思路，即采用多元高斯分布下的协方差矩阵(式(5))来替代没有解析式的高斯混合分布协方差矩阵，后面就可以直接衔接拉丁超立方抽样技术来生成与目标记录选取数量相同的模拟谱，抽样采用的均值目标谱采用完备条件谱的条件均值(式(11))。简化算法的计算流程如图7 所示。这样做虽然牺牲了协方差矩阵的构造精度，进而导致生成的模拟谱与目标理论分布存在一些差异，但是可以有效避免采用Bradley 两步蒙特卡罗模拟方法需要生成大量模拟谱才能逼近目标分布的弊端。由图9的算例可以看出，此方法所得到的模拟反应谱的均值、标准差与完备条件谱的目标基本一致。

图9 生成的模拟谱与完备条件谱对比Fig.9 Comparison of the simulated spectrum with exact conditional target spectrum

得到了模拟谱后，就可以采用贪心优化算法[14]做进一步的记录优选，最终得到满足条件的强震动记录集。贪心优化算法的步骤如下，对于模拟反应谱中的每一条反应谱，计算其与强震动记录库中的天然地震动记录反应谱在所考虑的全部周期谱加速度的误差值之和SSE，从强震记录数据库中选取与其最接近的一条，最终获得一个天然地震动记录集：

式中：lnSa(Ti)为所选记录周期Ti处谱加速度的对数值；(Ti)为模拟反应谱在周期Ti处的谱加速度的对数值；p为所考虑的振动周期点的个数；SSE为平方误差的总和。

当选取的地震动数量较少时，通过最小SSE得到记录的均值和标准差可能与目标谱略有偏差。因此，使用贪心优化算法来提高所选样本与目标谱之间的匹配度。贪心优化算法通过在迭代中不断地量化记录选取结果与目标之间的误差来得到一个局部的最优解。在初选得到的样本中，对每一条地震动进行替换，如果没有新的地震动使得SSEs改进，则保留样本中原来所选的地震动。记录选取结果与目标分布的误差SSEs如式(14)所示：

式中：SSEs为模拟反应谱与完备条件谱的误差总和；为选取记录反应谱周期Ti处谱加速度的对数值的均值；为选取记录反应谱周期Ti处谱加速度的对数值的标准差；μlnSa(Ti)|lnSa(T*)和σlnSa(Ti)|lnSa(T*)为周期Ti处目标条件谱的均值与条件标准差；w1、w2为控制各IM 指标权重的系数。

采用上述方法，针对前文构建的目标完备目标谱，数据库为NGA-west1，从7038 条记录中选取了20 条水平分量天然强震记录，权重设置为w1=1、w2=2。均值和标准差的匹配结果如图10 所示。可以看到经过贪心优化算法的优选之后，均值和标准差与目标基本一致，表明实现了较好的匹配效果。但是需要注意的是存在若干条记录具有较大离散性，该问题可以在记录选取初期设置上、下限值时进行初步筛选。

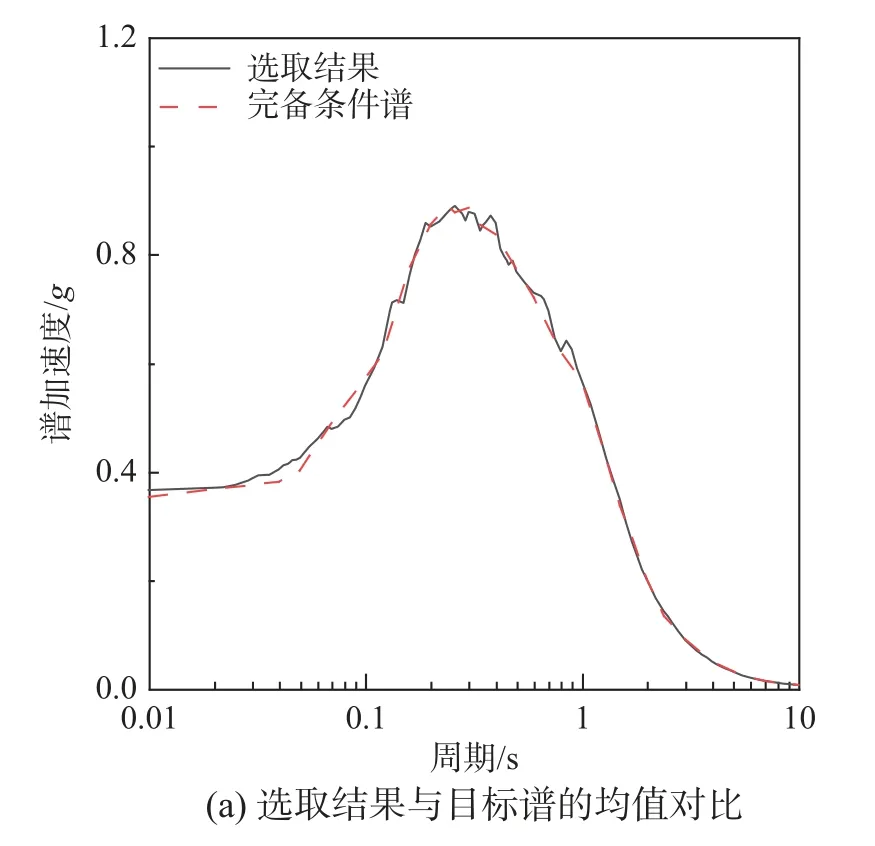
图10 匹配完备条件谱的天然强震动记录选取结果Fig.10 Results of selected ground motion matching exact conditional target spectrum

虽然本研究提出的简化算法可以实现均值与标准差的良好匹配，但仍然需要进一步衡量记录选取结果的反应谱分布与完备条件谱目标分布之间的差异。Kolmogorov-Smirnov 检验方法能够利用样本数据，推断样本来自的总体是否服从某一理论分布，通过比较选取的天然地震动记录的多个周期点Sa值的累积经验概率分布(Cumulative distribution function, CDF)曲线与目标之间的差异判断所选结果是否可靠。对于所选的天然地震动结果，如果CDF 曲线之间的偏差大于置信区间下的范围，则认为选取结果不可靠。天然地震动记录的选取结果在周期0.1 s、0.5 s、2.0 s 和5.0 s 的Sa的CDF 曲线如图11 所示。可以看出，除了Sa(5.0 s)外，在给定的显著性水平α=0.1 下，选取结果的Sa值分布基本都落在接受域中。因此，本研究提出的简化记录选取算法，虽然并没有以CDF作为记录选取的依据，但是同样实现了与目标分布较好的匹配效果。

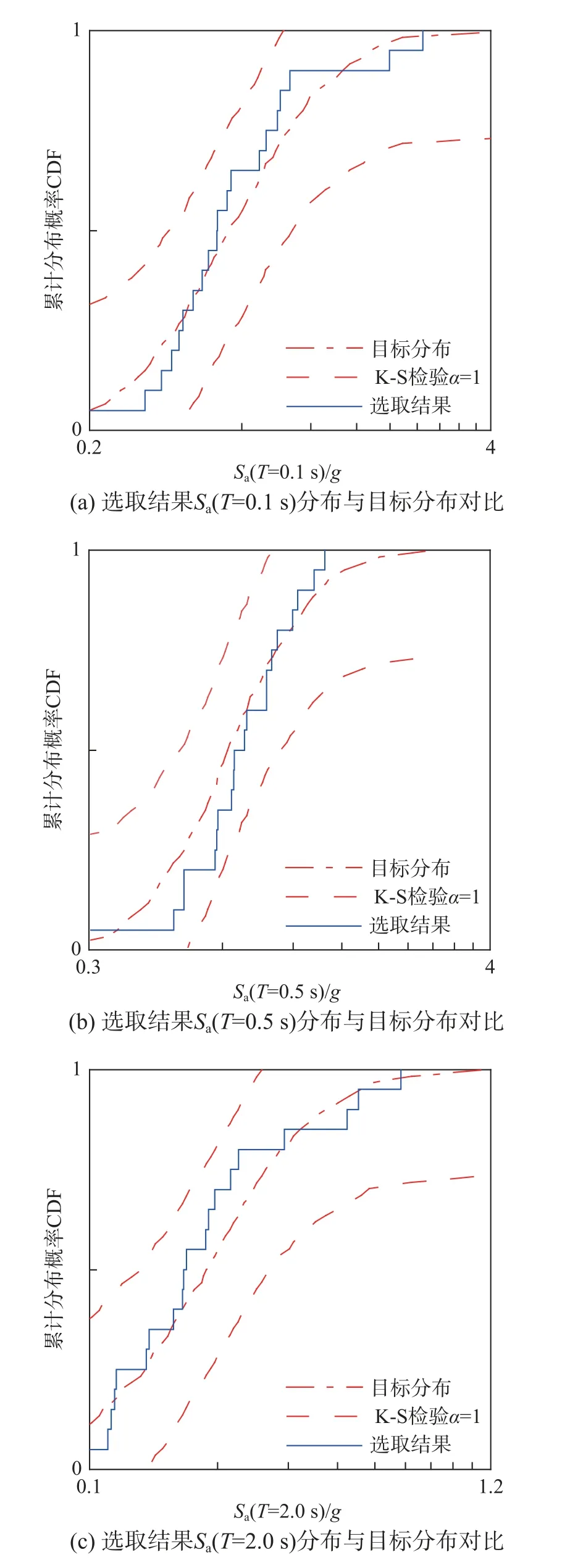
图11 选取结果在周期0.1 s、0.5 s、2.0 s 和5.0 s 与目标分布对比Fig.11 Comparison of the distribution in periods of 0.1 s,0.5 s, 2.0 s and 5.0 s with target

4 结论

本文与我国概率地震危险性分析的设定地震解耦结果相衔接，构造了考虑所有设定地震微元权重和潜源走向的完备条件目标谱，可以为场址危险一致地震动输入提供记录选取依据。相关工作与结论如下：

(1) 以北京近郊某城市为算例，构造了粗略条件目标谱与完备条件谱，对比结果表明：完备条件谱的均值介于分别使用长、短轴预测方程的粗略条件目标谱之间；完备条件谱的目标条件标准差要高于粗略条件谱。完备条件谱可以很好地体现潜源的空间分布特征与场址地震危险性之间差异。

(2) 对比了基于不同强震动记录数据库拟合得到的加速度反应谱相关系数模型对条件谱构造的影响。对比结果表明，不同相关系数模型下的精确条件谱以及粗略条件谱具有类似的谱型，但是基于我国JK17 模型得到的目标谱在0.5 s 附近区段是要略高于其他相关系数模型的结果的，而条件标准差结果反而要低于其他模型。当后续记录选取希望准确体现中国区域的地震动特征的时候，相关系数模型的这一差异是需要考虑的，建议采用基于中国数据拟合的JK17 模型计算。

(3) 针对中国完备条件目标谱的构造特点，给出了一种简化的天然强震动记录选取方案。采取多元高斯分布的协方差矩阵进行近似替换高斯混合分布的协方差矩阵，结合贪心优化算法进行记录优选，最终在实现均值、标准差的高效匹配的同时，在Sa指标分布方面也有较好的效果。较好实现了针对中国完备条件谱的记录选取。