近断层地震动作用下浅埋综合管廊地震易损性研究

张 海，王程西，王 岱，刘中宪，孟思博

(1.天津市土木建筑结构防护与加固重点实验室，天津 300384；2.天津城建大学土木工程学院基础设施防护和环境绿色生物技术国际联合研究中心，天津 300384)

历次地震中不乏地下综合管廊震害实例[1]，为此，诸多学者从地震输入[2-5]、结构体系[6-10]、工程场地[11-13]等方面研究了地下综合管廊的地震响应，袁勇等[14]进一步对目前综合管廊抗震分析研究进展进行了总结评述。众所周知，结构地震易损性分析有助于更早发现潜在风险并采取相应措施。因此，综合管廊等地下结构地震易损性研究也取得较为丰富的成果，如地铁车站[15-20]、隧道[21-25]、综合管廊[26]等。

针对地铁车站，HUH 等[15]以地面峰值加速度(Peak Ground Acceleration, PGA)作为地震动强度指标(Intensity Measure, IM)，以柱端塑性铰作为结构损伤指标(Damage Measure, DM)，研究分析了浅埋两层箱形结构的地震易损性；钟紫蓝等[16-18]采用增量动力分析(Incremental Dynamic Analysis，IDA)方法对地铁车站进行易损性分析，认为对于浅埋结构，地表PGA 宜为IM；陈之毅等[19]基于深度学习方法提出一种地震响应概率模型，采用正交化IM 选用贡献率最大的5 个相互正交主成分以此评价地铁车站易损性；JIANG 等[20]采用IDA方法进行了地铁车站地震易损性研究，结果表明：近场地震动对地铁车站具有更高的破坏概率。

针对隧道，王伯超等[21]采用IDA 方法对公路隧道进行易损性分析，认为PGA 宜作为IM；NGUYEN 等[22]以弯矩比为DM，通过分析箱形隧道结构的易损性，建议采用PGV/Vs30作为IM；HUANG 等[23]综合考虑PGA 和PGV，采用IDA方法计算分析了软土隧道的地震易损性，并进一步采用人工神经网络进行了研究，结果表明：PGV宜作为IM[24]；SILVA 等[25]采用有限差分法研究了软土隧道的地震易损性，研究表明，PGA 相关度最高。

针对综合管廊，张景威等[26]以PGA 为IM，以节点位移为DM，输入多条随机地震动进行非线性动力时程分析，研究了不同强度地震动作用下地下综合管廊结构的易损性。

由上述研究可知，目前地下结构地震易损性研究大多采用单一IM，且主要以PGA 为主；不同结构体系的抗震薄弱位置不同，DM 的选取也不尽相同。目前综合管廊损伤状态的判定尚缺乏明确的规范要求，而且对于近断层地震动作用下综合管廊地震易损性的研究仍比较匮乏。因此，本文针对地下双层综合管廊，以最大层间位移角作为DM，采用IDA 方法[27]进行结构地震易损性分析，从而为近断层地震动作用下综合管廊地震损伤预测提供参考。

1 数值模型与地震输入

1.1 数值模型

图1 为地下综合管廊场地模型示意图[28]。利用ABAQUS 建立土-综合管廊三维有限元模型[29-30]，模型上表面为自由边界，两侧及底面均采用粘弹性边界[31]，地震输入则通过等效节点力在边界输入[32]。其中，土体和管廊均采用C3D8R 单元，钢筋采用T3D2 单元进行模拟；土体选用Mohr-Coulomb 本构模型，C35 混凝土选用损伤塑性模型(Concrete Damaged Plasticity, CDP)；钢筋选用HRB335，采用无屈服点弹塑性本构模型；接触采用ABAQUS 自带的面与面接触，法向为Hard，切向为Penalty，摩擦系数为0.4。具体材料参数见表1。

表1 材料参数Table 1 Material parameters

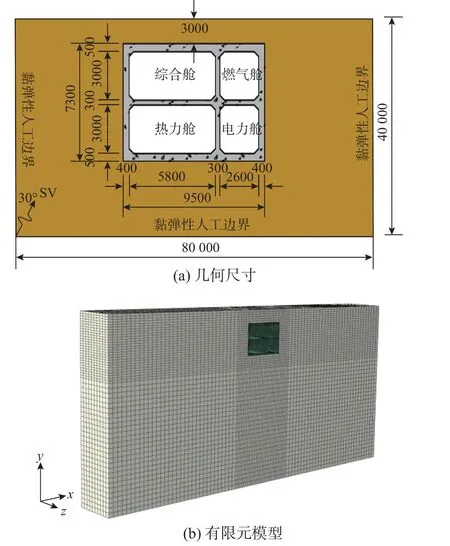
图1 地下综合管廊模型 /mmFig.1 The model of underground utility tunnel

1.2 地震输入

参考黄景琦等[33]关于斜入射地震波对地铁车站结构的不利影响，本文分析地下综合管廊在30 度斜入射SV 波作用下的动力响应。

根据场地条件、地震动强度、震中距大小为主要参考指标，参考FEMA P-58-1[34]从太平洋地震工程研究中心(Pacific Earthquake Engineering Research Center, PEER)选取了12 条近断层地震动记录[35](表2)，其加速度反应谱曲线如图2 所示。首先对12 条地震波进行截波及基线校正，而后进行调幅：①对峰值加速度(PGA)按比例调整为0.1g～1.0g(g=9.8 m/s2)范围内10 个不同峰值的地震动；②对谱加速度(Sa)按比例调整为0.3g～3.0g范围内10 个不同峰值的地震动，最后分别将240 条调幅地震波作为地震输入进行增量动力分析。

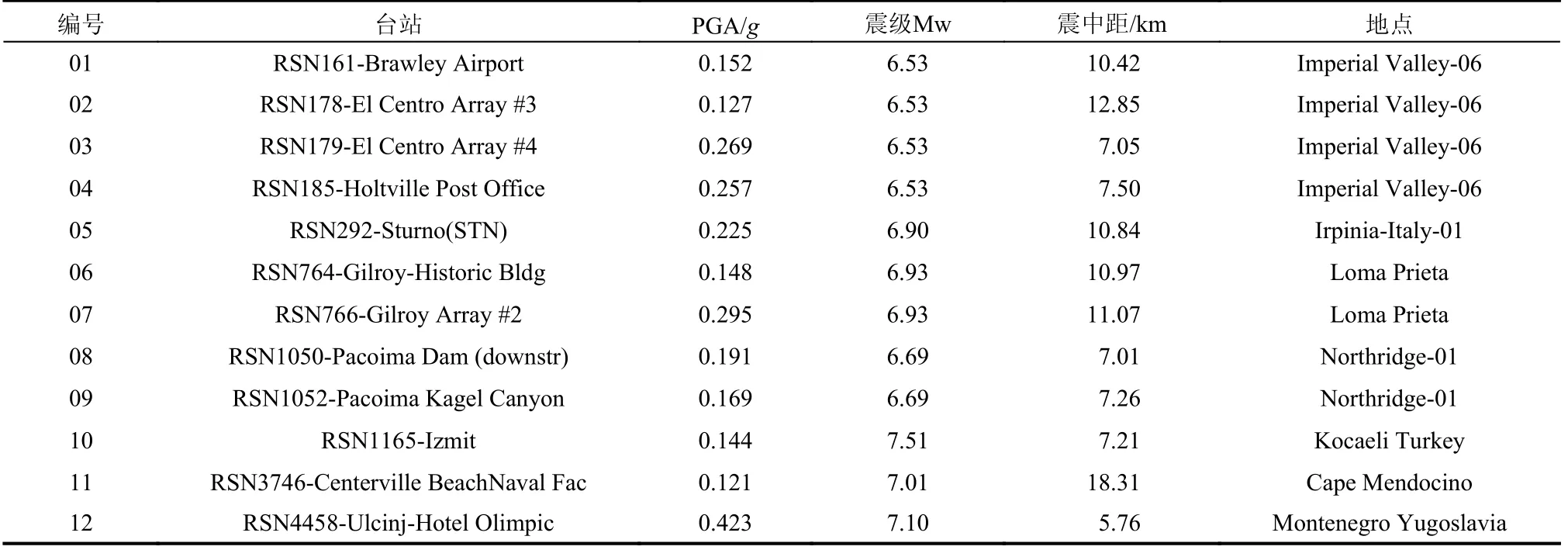
表2 近断层地震动记录Table 2 Near-fault ground motion records

图2 近断层地震动加速度反应谱Fig.2 Acceleration response spectra of near-fault ground motion

2 地下综合管廊的易损性分析

2.1 地震动强度指标选取与抗震性能水平划分

地震动强度指标(IM)的选取在一定程度上决定了易损性分析的结果是否可靠[17]，本文选取加速度型、速度型及位移型三类共计9 种地震动强度指标，即地面峰值加速度(PGA)、谱加速度(Sa)、均方根加速度(Arms)、地面峰值速度(PGV)、谱速度(Sv)、均方根速度(Vrms)、地面峰值位移(PGD)、谱位移(Sd)和均方根位移(Drms)。通过对比其作为地震动强度指标时对IDA 分析结果的离散性，确定出最合理的地震动强度指标[26]。本文选用层间位移角最大值θmax作为DM。

根据结构损伤指标和地震动强度指标近似满足幂函数关系[36]，进行对数线性回归并计算标准差。表3 给出了9 种地震动强度指标对应的标准差 βD，可以看出，加速度型指标的离散性小于速度型指标小于位移型指标，因此，本文易损性分析选用PGA 和Sa 作为IM。

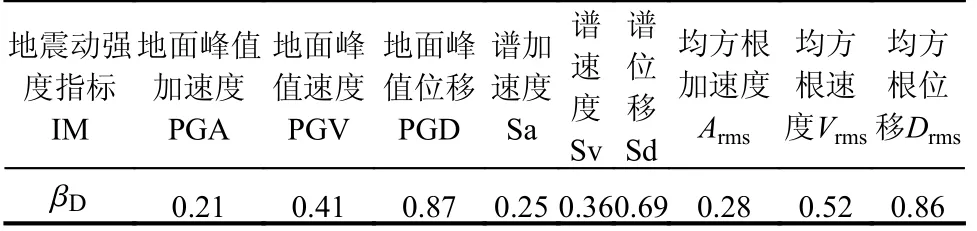
表3 地震动强度参数标准差Table 3 Standard deviation of parameters of ground motion intensity

将地下结构的抗震性能水平划分为四级[26,34]，即基本完好(OP)、轻微损坏(IO)、生命安全(LS)和防止倒塌(CP)。采用Pushover 法对综合管廊不同性能水平所对应的层间位移角限值进行标定[37-38]，可得到四个性能水平对应的层间位移角限值分别为0.000 31、0.000 45、0.001 26 和0.002 28。

2.2 以PGA 或Sa 为IM 的综合管廊易损性分析

浅埋地下结构地震易损性曲线近似服从对数正态分布[18,39-40]，即结构响应超越性能水平极限值的超越概率可表示为：

式中：dS为在给定地震动强度S下结构的地震响应；dSi为结构性能水准的临界值；Smi为结构处于某个性能水平限值； βtot为总的对数正态标准偏差。

经过一元线性回归分析得到基于PGA 或Sa 的易损性分析回归方程为：

将不同地震动的PGA 和Sa 分别代入式(2)和式(3)，再根据式(1)计算超越概率。

图3 给出了不同抗震性能水平下的综合管廊结构地震易损性曲线。根据前文定义的四级性能水平指标，可将综合管廊结构的损伤状态划分为五个等级，即基本完好、轻微破坏、中等破坏、严重破坏、倒塌。可以看出，结构易损性曲线的形状随着结构损伤状态的严重而呈现平缓的趋势；随着PGA 或Sa 的增大，综合管廊的各个性能水平的超越概率也逐渐增大，当PGA<0.3g或Sa<0.9g时，OP 和IO 状态下易损性曲线比较陡峭，超越概率快速增大，表明综合管廊的破坏向着更为严重的状态发展。

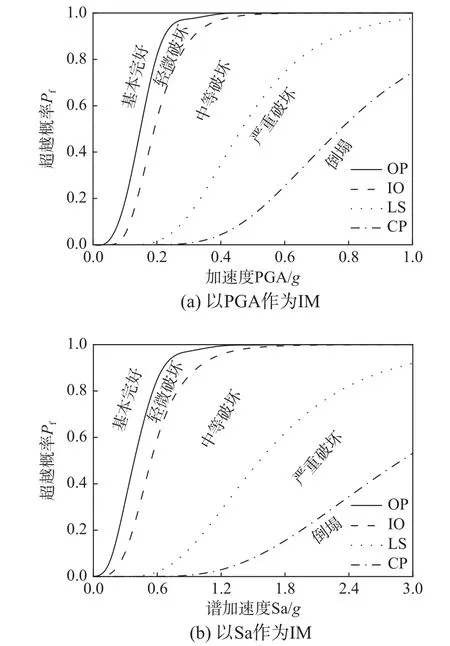
图3 以PGA 或Sa 为IM 的综合管廊结构地震易损性曲线Fig.3 Seismic fragility curve of utility tunnel structure with PGA or Sa as IM

2.3 基于神经网络的综合管廊易损性分析

当分别考虑峰值加速度、土体剪切模量等多个参数对综合管廊结构易损性的影响时，采用有限元计算综合管廊地震响应则需要大量的计算耗时，因此，以有限元计算数据为训练样本，基于BP 神经网络来预测综合管廊的地震损伤，则不失为一种简捷高效方法。众所周知，神经网络在预测过程中会存在不确定性，但从整体来看，相关性随训练数据集的增加而逐渐增加[41]。

表4 给出了输入参数即地震动强度指标PGA、Sa 及土体剪切模量G选取的基准值和变化范围，通过训练完成后的神经网络模型对各工况下的层间位移角进行预测。本文将600 个样本集作为训练数据，随机分配为训练集和测试集。其中，480个样本作为训练集供神经网络进行学习，120 个样本作为测试集用来测试神经网络的训练精度，训练数据集占比为80%。

表4 输入参数的基准值和变化范围Table 4 The reference value and variation range of input parameter

将PGA、Sa 及土体剪切模量G三个影响因素作为输入参数，用于反映地震动不确定性及场地不确定性[42]，将有限元计算得到的综合管廊层间位移角最大值作为输出参数，建立包含输入层、隐含层和输出层的三层神经网络，网络模型参数为：① 输入层含3 个节点，输出层含1 个节点，隐含层含10 个节点；② 最大迭代步数为1000 步；③ 学习速率设置为0.01；④ 误差容许值为0.0001；⑤ 动量常数设置为0.5。基于以上参数对神经网络进行训练，训练的归一化结果如图4 所示。通过实际值与预测值进行拟合分别得到3 条拟合曲线，虚线为理想条件下实际值与预测值相等的情况，结果表明，训练、测试及所有样本数据的相关系数均在0.9 以上，拟合效果较好，建立的关系模型可靠。

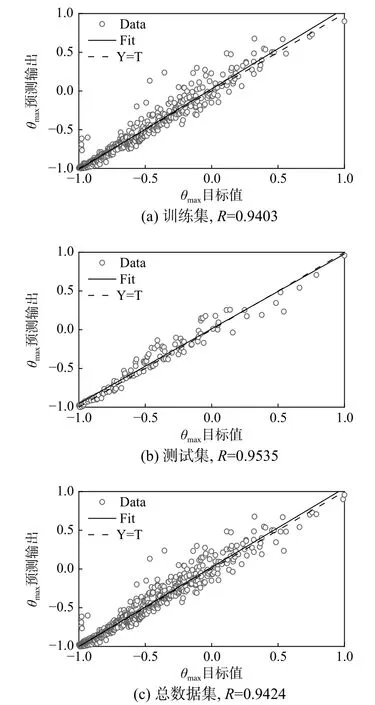
图4 BP 神经网络回归结果Fig.4 Regression results derived by BP neural network

图5 给出了神经网络预测值与有限元计算值(输入其它地震波)的对比。其中，神经网络预测值与有限元计算值最大相对误差为16.57%，神经网络的预测值与实际值误差不大，训练结果较为良好，能够在一定程度预测计算结果，可以作为地下综合管廊易损性分析的辅助工具进行初步评估。

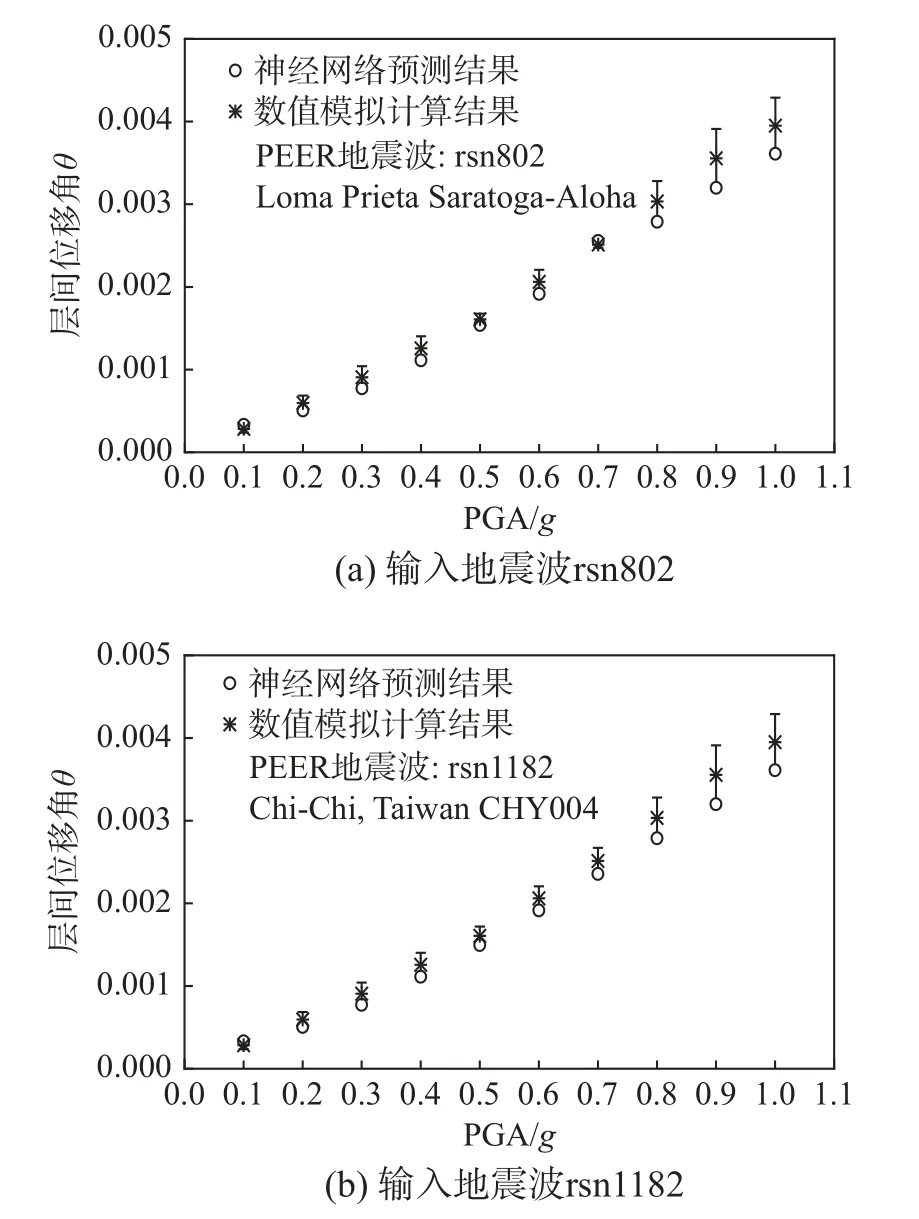
图5 BP 神经网络预测值与有限元计算值对比Fig.5 Comparison between the predictive values by BP neural network and the ones calculated by FEM

图6 给出了由神经网络预测数据计算得出的易损性曲线。可以看出，土体剪切模量对易损性曲线的影响非常显著，随着土体剪切模量的增大，超越概率变化区间范围增大。土体剪切模量对OP、IO 损伤状态的影响明显小于LS、CP 两种损伤状态，OP、IO 状态下易损性曲线较为陡峭，说明此状态易达到；在OP 状态下，当地震动峰值加速度超过0.5g时，五种场地土对应的结构超越概率均趋于1，管廊不能保持OP 状态；在IO 状态下，只有地震动强度足够大(约超0.7g)时，五种场地土对应的结构超越概率方趋于1，管廊不能保持IO 状态，向更严重的破坏状态发展。LS、CP 的易损性曲线较为平缓，结构进入塑性变形阶段，当地震动强度一定时，随着土体剪切模量的增大，超越概率逐渐减小(表5)，说明场地土越硬，对结构抗震越有利。因此，实际工程选址时应充分结合现场勘查确定所选场地是否合理。

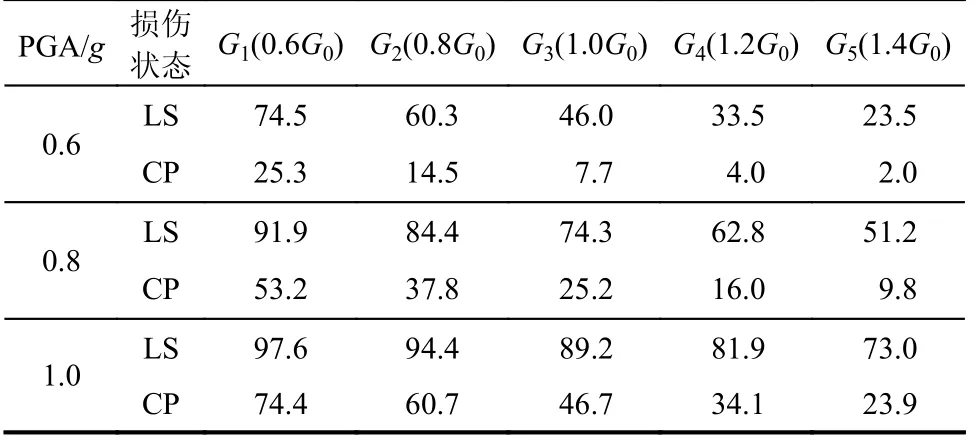
表5 不同场地土对应的综合管廊LS、CP状态超越概率/(%)Table 5 Exceedance probability of utility tunnel at LS and CP states for different site soils

图6 不同场地土对应的综合管廊结构地震易损性曲线Fig.6 Seismic fragility curve of utility tunnel structure for different site soils

2.4 以PGA 和Sa 为IM 的综合管廊易损性分析

以PGA 和Sa 作为地震动强度指标，分别记为IM1=im1和IM2=im2，θmax为结构损伤指标。对其进行回归分析得到：

将不同地震动的PGA 和Sa 代入式(4)得出θmax，而后根据式(5)计算超越概率，得到不同性能水平下的易损性曲面(图7)。从图7 可以看出，随着地震动强度PGA、Sa 的逐渐增大，超越概率不断增大。四种不同损伤状态下两侧易损性曲线陡峭程度也很相似，说明PGA 和Sa 对综合管廊超越概率的影响程度也相似。值得一提的是，地震动强度指标PGA、Sa 及土体剪切模量G的变化对易损性分析的敏感度贡献分别为37.89%、34.99%、27.12%。

图7 以PGA 和Sa 为IM 的综合管廊结构地震易损性曲面Fig.7 Structural fragility surface of utility tunnel with both PGA and Sa as IM

图8 给出了Sa=0.6g、1.2g、1.8g、2.4g及3.0g时的综合管廊结构地震易损性曲线。可以看出，超越概率随着Sa 的增大而增大，而单一IM对应的超越概率较大，显然，忽略Sa 的影响有可能高估结构的损伤。当PGA=0.11g时(多遇地震)管廊受到轻微破坏的最大概率为18.12%，倒塌概率为0，管廊能够保持OP 状态；当PGA=0.3g时(设防地震)管廊不能保持OP 状态，当Sa 大于1.2g时管廊超越IO 状态概率在60%以上，管廊易达到轻微损伤，在LS 状态下仅当Sa 为3.0g左右时管廊超越概率为17.36%，在设防地震作用下基本达不到CP 状态；当PGA=0.51g时(罕遇地震)管廊均不能保持OP、IO 状态，在LS 状态下Sa=2.4g和3.0g时管廊发生严重破坏的概率分别为48.92%和67.13%，管廊发生严重破坏可能性较大，应重点关注，在CP 状态下，Sa 小于2.4g时管廊相对安全，当Sa 在3.0g左右时管廊发生倒塌的概率为20.29%。因此，为准确评估地下结构的抗震性能，建议地下结构易损性分析应综合考虑PGA 和Sa 的影响。

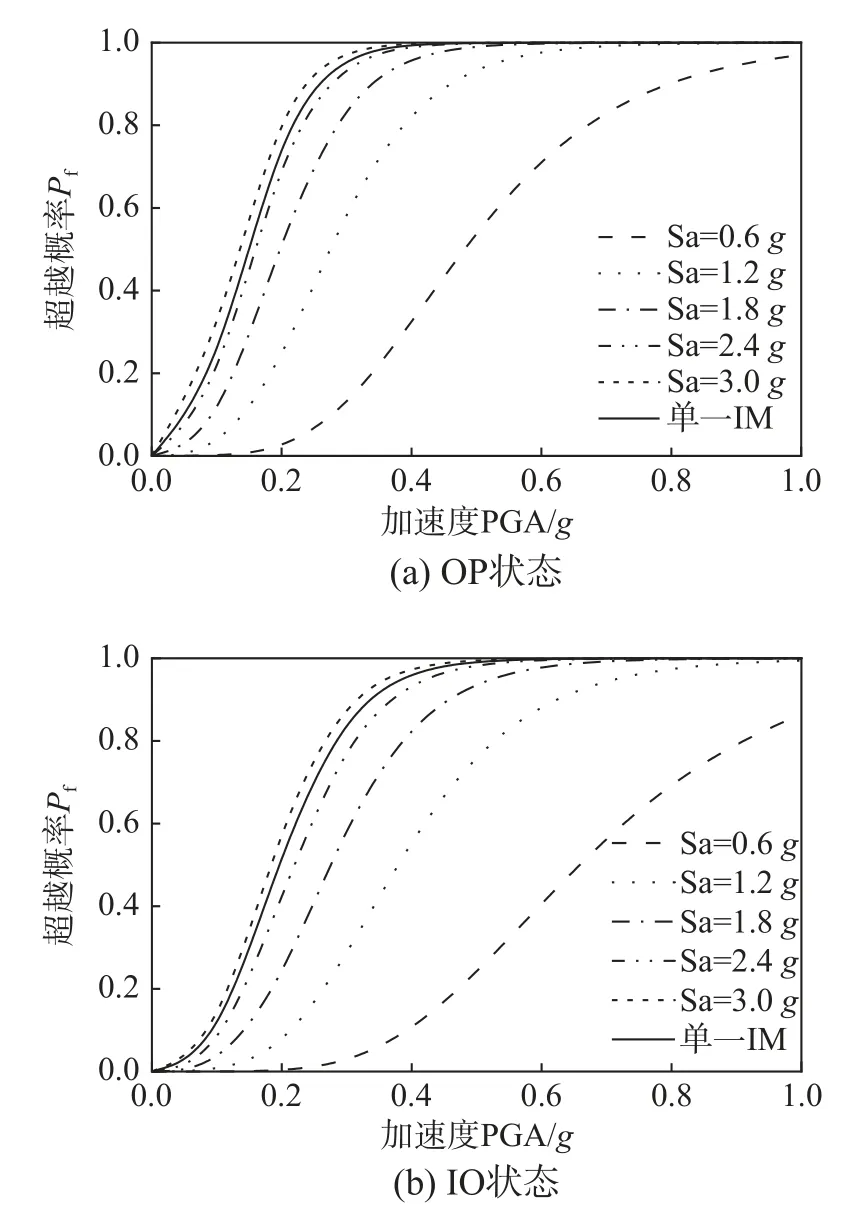
图8 Sa 不同时的综合管廊结构地震易损性曲线Fig.8 Seismic fragility curve of utility tunnel structure for different Sa

3 结论

本文以近断层地震动为输入，采用有限元法对浅埋双层综合管廊进行非线性动力时程分析，并采用IDA 方法进行结构易损性分析，给出不同地震动强度下浅埋双层综合管廊结构的破坏概率，为综合管廊等地下结构的地震损伤预测提供参考。相关研究结论如下：

(1) 地震动强度指标的离散性：加速度型指标＜速度型指标＜位移型指标，建议进行综合管廊等浅埋地下结构地震易损性分析时，选取加速度型指标PGA、Sa 作为地震动强度指标。

(2) PGA、Sa 及土体剪切模量对综合管廊结构地震易损性分析结果影响明显，随着土体剪切模量的增大，超越概率逐渐减小，且LS、CP 状态超越概率变化范围要明显大于OP、IO 状态。值得一提的是，神经网络预测具有较高的可靠性(90%以上)，可对综合管廊等地下结构地震损伤进行快速预测。

(3) 考虑PGA 和Sa 双参数的地震易损性分析能综合反映不同地震动强度指标对结构损伤超越概率的影响，而相比之下，仅考虑PGA 或Sa 单参数影响所得出的超越概率偏大，可能高估结构损伤程度。因此，在综合管廊等浅埋地下结构地震易损性分析中，建议同时考虑PGA 和Sa 的影响。