基于主动学习Kriging 模型的改进一次可靠度方法

刘 丞，范文亮,2，余书君，李正良,2

(1.重庆大学土木工程学院，重庆 400045；2.山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆 400045)

工程结构可靠度分析的主要目标是估计包含各类不确定性随机变量的实际工程结构的失效概率[1-2]。针对此类问题，已发展了一次可靠度方法(FORM)[3-6]、二次可靠度方法(SORM)[7-10]、代理模型方法[11-13]、矩方法[14-15]和蒙特卡罗模拟方法(MCS)[16-18]等一系列结构可靠度分析方法。

迄今为止，一次可靠度方法仍是应用最为广泛的可靠度分析方法。其中，HASOFER 和LIND[3]首先提出了一类验算点迭代算法-验算点法，通过在标准正态空间中搜索从原点到极限状态曲面的最小距离来获得验算点坐标，结构的失效概率可通过该最小距离解析计算。RACKWITZ 和FLESSLER[5]将该算法进一步扩展到了非正态随机变量的一般情况，即HLRF 方法。若引入Rosenblatt 变换[19]或Nataf 变换[20-21]，亦可将其方便地拓展至相关变量情形。上述一次可靠度方法的迭代过程简单、易于实现，但需求解迭代过程中所有迭代点处的函数值和梯度值，且对于隐式功能函数的梯度值计算尚需引入差分法[22]，计算效率不很理想。引入代理模型是改善一次可靠度方法效率的有效途径之一。目前，将代理模型中的Kriging 模型与一次可靠度方法相结合主要有两种方式：其一，通过随机选定的点集建立Kriging 模型，并以此模型近似计算迭代点处的函数值和梯度值，从而实现可靠度分析[23]；其二，通过随机选定的初始点集建立初始Kriging 模型，以此模型计算梯度值并确定新的迭代点，并将迭代点的计算结果用于更新Kriging 模型，从而实现验算点的搜索[24]。仔细考察不难发现，前者可视为Kriging 模型和一次可靠度方法的简单组合，由于仅由随机点集进行Kriging 模型的一次建模，计算精度依赖于该Kriging 模型对功能函数的近似精度，此外由于点集的随机性必然导致计算结果的随机性；后者则将Kriging 模型和一次可靠度的迭代过程实现了较好的融合，但初始点集的随机性依然会导致计算效率的随机性，且若初始Kriging 模型精度不高时可能会弱化一次可靠度方法的收敛性能，此外该方法未能充分利用Kriging 模型的统计特性。

图1 示出了一次可靠度分析的典型迭代收敛过程(即后文中算例1 中工况1 的迭代收敛结果)，仔细考察不难发现，整个迭代过程可分为两个阶段：1)全局搜索阶段，即前期迭代阶段，此阶段相邻迭代点相距较远；2)局部搜索阶段，即后期迭代阶段，此阶段迭代点在一个较小的局部区域内波动。若以全局搜索阶段的迭代点为基础建立Kriging 模型，且充分利用该模型的统计特性进行Kriging 模型的主动学习，进而实现局部搜索阶段迭代点的函数值及梯度值的自适应计算，将有助于改善一次可靠度方法的计算效率。为此，基于上述思路，本文提出了一种基于主动学习Kriging模型的改进一次可靠度方法。

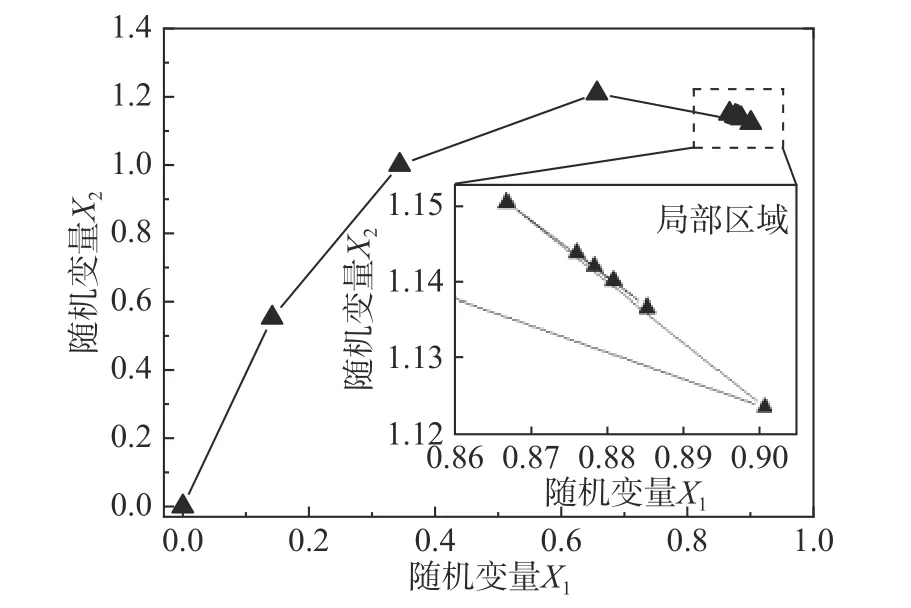
图1 一次可靠度方法迭代过程Fig.1 Iterative process of FORM

1 通用一次可靠度方法

假设结构可靠度问题的功能函数为：

式中：X={X1,X2,…,Xn}为基本随机向量；n为随机变量的数量。对Xi引入等概率变换，即：

式中：Ui为与Xi对应的标准正态变量；Φ(·)为其累积分布函数；为Xi的累积分布函数Fi(·)的反函数。于是，式(1)可改写为：

式中：U={U1,U2,…,Un}，且Ui和Uj的相关系数ρU,ij可由Xi和Xj的相关系数ρX,ij依下式确定，即[25]：

式中：µi和σi分别为Xi的均值和标准差；Hk(·)为Hermite 多项式；φ(·)为标准正态变量的概率密度函数；mi为由Xi的分布确定的常数。

式(3)所对应的可靠指标β 和验算点u＊为[20]：

显然，u*=和β 需由式(6)～式(8)迭代确定。后文中将在迭代过程中由式(8)更新的点称为迭代点。由式(6)和式(7)可见，在每一迭代步中均涉及h(U)在迭代点处的函数值和梯度值。

若h(U)为隐式功能函数，则u*处的梯度值可由差分法计算如下：

2 基于主动学习Kriging 模型的改进一次可靠度方法

考虑到一次可靠度方法在迭代搜索验算点时的收敛特性，可将迭代过程分为全局搜索阶段和局部搜索阶段两部分。文中以第k次迭代点u(k)与第k-1 次迭代点u(k-1)的距离||u(k)-u(k-1)||达到某一较小的阈值c作为两个阶段的划分准则，若||u(k)-u(k-1)||≥c，则属于全局搜索阶段，否则属于局部搜索阶段。文中取c=0.1。

2.1 全局搜索阶段

在全局搜索阶段，以均值点u(1)为初始迭代点，按照第1 节的通用一次可靠度方法确定迭代点，直至达到||u(k)-u(k-1)||<0.1。且将此阶段最终的k值记为q。

2.2 局部搜索阶段

在局部搜索阶段，将全局搜索阶段的迭代点{u(1),u(2),…,u(q-1)}及在迭代点处计算梯度值的差分点作为初始训练点集，基于此建立初始Kriging 模型，根据Kriging 模型在后续迭代点处的预测精确性自适应地更新模型并借助更新后的Kriging 模型提供预测值和梯度值，将Kriging 模型的更新与通用一次可靠度方法的迭代融合在一起，直至收敛。

2.2.1 初始Kriging 模型

为简便，将初始训练点集记为u={u(1),u(2),···,u(M)}，相应函数值其中M=(n+ 1) (q- 1)，由此可得h(U)的Kriging 模型(U)为[26-28]：

式中：f(U)为U的多项式基函数，文中取f(U)=[1,U]；P为回归系数向量；m(U)为方差为σ2的零均值高斯过程，其协方差满足：

式中：Rθ(u(i),u(j))为含参数θ 的相关函数方程，文中采用高斯相关函数，即：

由式(10)可给出h(U)在任意点u处的预测值和标准差，即：

式中：F为M×n维基函数矩阵；R为训练点之间相关函数矩阵；r为u与各训练点之间的相关函数列向量；R与r可分别表示为：

此外，由式(10)可知u处的函数值z满足：

Kriging 模型的详细介绍可参考文献[26 - 27]，且Kriging 模型的建模及运算均可由MATLAB 软件的DACE 工具箱实现。

根据显式表达式(13)，可方便地推导出梯度的显式表达式；由于梯度值的计算亦可由DACE工具箱直接计算，其表达式不再详述。

实用中，利用DACE 工具箱计算Kriging 模型在u处的预测值、梯度值以及方差命令为“[y,dy,mse]=predictor(u,dmodel)”。

2.2.2 Kriging 模型的误差估计

为考察Kriging 模型在u处的预测精确性，令：

由式(17)可得：

式中，Pr{·}表示概率。若取S(u)=50，则z的误差小于6%的概率达到99.7%。

值得指出的是，在AK-MCS[29]方法中，尽管Kriging 模型是针对功能函数建立的，但是其误差估计是针对功能函数的示性函数展开的[29-30]，因此仅适用于主动学习Kriging 模型(AK)与Monte Carlo 模拟(MCS)相结合的方法中。相比较而言，文中的式(19)直接针对功能函数进行误差估计，为主动学习Kriging 模型与其他类型可靠度分析方法的结合奠定了基础。

2.2.3 Kriging 模型的更新

同理，若已得到第l次更新的Kriging 模型(U)及与之对应的迭代点u(q+l)，可根据式(18)计算(U)在u(q+l)处的S(u(q+l))，并根据S(u(q+l))进行Kriging 模型更新，即：

式中，P(l+1)、m(U)(l+1)为将u(q+l)加入训练点集重新更新后P、m(U)的对应项。

不难发现，上述的Kriging 模型更新属于基于主动学习的Kriging 模型更新，S(·)则对应着其中的学习函数。

2.3 改进一次可靠度方法实现流程图

综合全局搜索阶段与局部搜索阶段，本文建议的改进一次可靠度方法的流程图如图2 所示。

图2 改进一次可靠度方法流程图Fig.2 Flow chart of the improved FORM

仔细考察不难发现，改进一次可靠度方法尽管引入了Kriging 模型，但是Kriging 模型所需的初始训练点集以及训练点的增加过程均是确定的，因此该方法的计算结果亦是确定的，与文献[23 - 24]的随机性结果具有显著区别。

3 算例分析

文中分别通过数值算例和工程算例验证建议方法的有效性，其中各算例均视为隐式功能函数情形。为考察改进一次可靠度方法的精度与效率，将其与通用的一次可靠度方法[21](即第1 节介绍方法，记为FORM)以及两种Kriging 模型与一次可靠度方法相结合的方法(即文献[23]和文献[24]的方法)进行对比。文献[23]采用LHS 方法抽取N1个样本点，计算对应的响应值并构建Kriging 模型，利用Kriging 模型替代功能函数并结合一次可靠度方法进行可靠度计算；文献[24]采用蒙特卡洛法随机抽取N2个样本点(N2≥n+1)，计算对应的响应值并构建Kriging 模型，基于此模型计算梯度值并结合一次可靠度方法确定新的迭代点，并将迭代点的计算结果用于更新Kriging 模型。显然，样本点集的随机性必然导致Kriging 模型的随机性，因此，与FORM 不同，文献[23]与文献[24]的计算结果是随机的。

由于文献[23]和文献[24]方法不适用于相关变量情形，因此将两种方法中的一次可靠度方法代之以文献[20]的通用一次可靠度方法，且分别简称为K-FORM-1 和K-FORM-2。由于文献[23]中未给出随机点数量的确定准则，后文中的K-FORM-1均采用30 个样本。为了算法比较的公平性，各方法迭代过程的收敛准则统一采用||u(k+1)-u(k)||<10-6。

各方法精度比较时，以抽样数为108的蒙特卡洛模拟方法(记为MCS)结果作为标准解，各方法的误差为：

式中：Value 为对应方法的可靠指标；MCS 为蒙特卡洛模拟方法计算的可靠指标。

各方法效率比较时，主要考察其调用功能函数的次数。此外，由于K-FORM-1 和K-FORM-2中初始选点的随机性导致可靠度计算结果在精度与效率上产生随机性。因此为了体现其随机性，上述两种方法的可靠度计算结果均为分别运算5 次的均值。

算例1.数值算例

考察如下功能函数[2,31]：

式中：X1～N(0,0.5),X2～N(0,0.5)且变量相互独立。根据k值的不同可分为2 种工况。

1)工况1：k=5

本文建议方法基于FORM 在全局搜索阶段迭代5 次后，迭代点u(6)与u(5)之间的距离(||u(6)-u(5)||=0.0863<0.1)满足设定精度，进入局部搜索阶段。在局部搜索阶段基于改进一次可靠度方法继续迭代了7 次，其中调用功能函数计算迭代点函数值并以此更新Kriging 模型4 次，因此本文建议方法的函数调用次数为5×(1+2)+4=19。结果示于表1。此外，表1 亦给出了抽样次数为108的MCS、FORM、K-FORM-1 和K-FORM-2 的计算结果；表2 给出了K-FORM-1 和K-FORM-2 各5 次运算的结果，其中由于K-FORM-1 各次运算效率相同，因此仅给出可靠指标，K-FORM-2 各次的可靠指标基本相同，因此仅给出功能函数调用次数。不难发现，建议方法与FORM 精度一致但效率最高；K-FORM-1 在与FORM 效率一致时，其精度是变化的，但总体而言，略低于FORM；K-FORM-2 与FORM 精度一致且效率高于FORM，但其效率是变化的。

表1 工况1 的可靠度计算结果Table 1 Reliability results for Case 1

表2 已有方法的随机性分析Table 2 Stochastic analysis of existing methods

2)工况2：k=10

各类方法的计算结果如表3 所示，K-FORM-1和K-FORM-2 各5 次运算的结果示于表2；其中，由于K-FORM-1 的5 次运算中仅2 次收敛，因此表3 中K-FORM-1 的结果为这2 次运算的平均值，而K-FORM-2 的5 次运算均不收敛。由上述结果可知，对于此工况，建议方法与FORM 精度基本相当，但效率显著提升；而在工况1 中较FORM 更优的K-FORM-2 不能给出收敛的结果；K-FORM-1 仍存在精度不高的问题，同时收敛性亦受到影响。

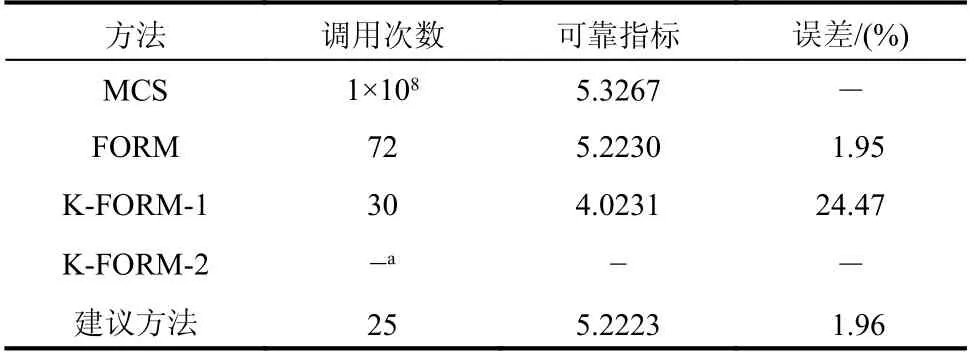
表3 工况2 的可靠度计算结果Table 3 Reliability results for Case 2

总体而言，算例1 的两种工况对比验证了本文建议方法能够在保证精度与FORM 一致的情况下显著提高计算效率；且相比K-FORM-1 和K-FORM-2，既避免了结果的随机性，尚能更好地兼顾精度、效率与收敛性。

算例2.抗力-效应工程算例

已知某工程功能函数形式为[1-2]：

式中：永久荷载效应G服从正态分布，µG= 5.3，σG=0.371；可变荷载效应Q服从极值Ⅰ型分布，µQ= 7，σQ= 2.03；抗力R服从对数正态分布，µR=30.92，σR= 5.26。

各类方法的计算结果如表4 所示。由于K-FORM-1 和K-FORM-2 在计算结果的精度与效率上分别存在随机性，因此将两种方法各5 次运算的结果示于表5。不难发现，建议方法与FORM精度一致但效率最高；K-FORM-1 相比FORM 而言计算效率有所提高，但其精度具有随机性，且平均误差大于FORM；K-FORM-2 与FORM 精度一致且效率高于FORM，但其效率具有随机性。比较而言，建议方法既避免了结果的随机性，尚能更好地兼顾精度、效率。

表4 算例2 的可靠度计算结果Table 4 Reliability results for Example 2

表5 已有方法的随机性分析Table 5 Stochastic analysis of existing methods

算例3.柔性基础沉降算例

考虑一个矩形基础沉降问题，功能函数为[32]：

式中：基础宽度B为30 m；基础长度L为40 m；基础嵌入深度D为3 m；地层厚度H为10 m；角数m为4；影响因素I1、I2和IF分别为0.073、0.089、0.95；均布荷载q0服从均值为280 kPa、标准差为40 kPa 的极值I 型分布，泊松比ν服从均值为0.25、标准差为0.08 的正态分布，弹性模量Es服从均值为80 MPa、标准差为2.5 MPa 的对数正态分布。

各类方法的计算结果如表6 所示，其中K-FORM-1 进行5 次运算的可靠指标在[3.4018,3.4163]内波动，K-FORM-2 进行5 次运算的函数调用次数在[23, 27]内波动。比较而言，不难发现各方法精度基本相当；建议方法仍然效率最高，K-FORM-2 优于K-FORM-1，且两者均优于FORM。

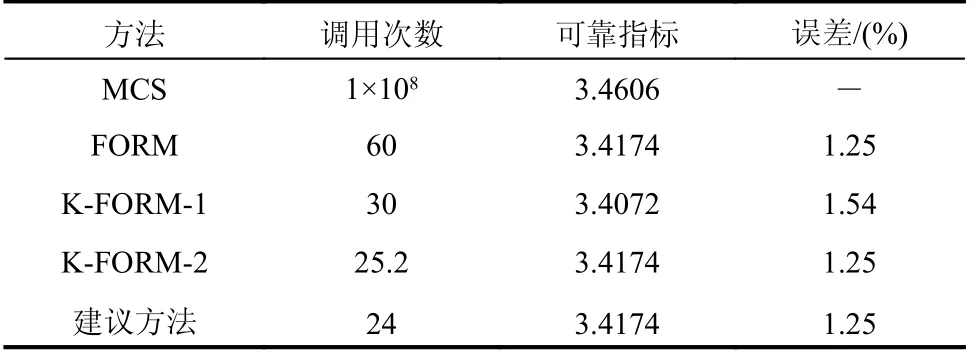
表6 算例3 的可靠度计算结果Table 6 Reliability results for Example 3

算例4.矩形截面悬臂梁算例

考察如图3 所示的矩形截面弹性悬臂梁的位移可靠度问题，功能函数为[21]：

图3 矩形截面悬臂梁Fig.3 Cantilever beam with rectangular section

式中：L为梁的跨度；q为均布荷载；E为材料的弹性模量；b、h分别为截面的宽和高，假设上述变量中E、L为确定性变量，分别取值为2.6×105MPa、6000 mm。q服从均值为1000 kN/m、标准差为200 kN/m 的对数正态分布，h服从均值250 mm、标准差为37.5 mm 的对数正态分布，b服从均值为100 mm、标准差为20 mm 的正态分布。假设b和h为相关变量，相关系数为0.6。

各类方法的计算结果如表7 所示。其中，采用建议方法时，由式(4)确定的等效相关系数为0.61888，与文献[33]直接求解二维积分方程得到的结果0.61887 非常吻合。

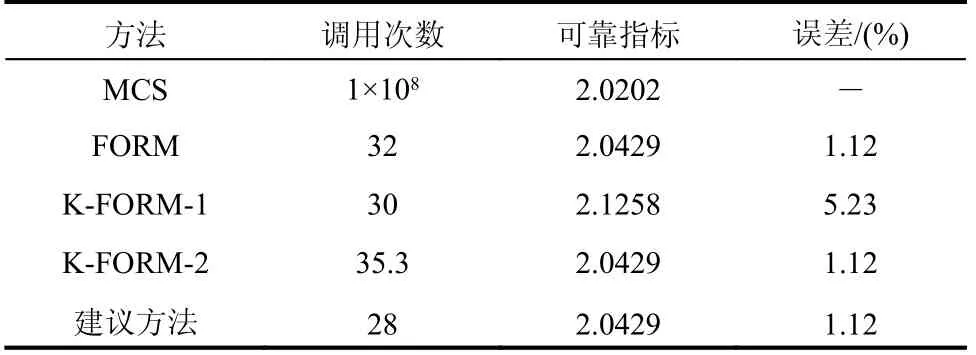
表7 算例4 的可靠度计算结果Table 7 Reliability results for Example 4

由表7 结果可知，建议方法与FORM 精度一致但效率最高；K-FORM-1 在效率上略高于FORM，但其精度低于FORM 且具有随机性；K-FORM-2与FORM 精度一致但效率低于FORM，且其效率亦具有随机性。

4 结论

为了进一步提高一次可靠度方法在可靠度分析时的计算效率，本文将一次可靠度方法分为全局搜索阶段和局部搜索阶段，在全局搜索阶段沿用通用的一次可靠度方法迭代过程，在局部搜索阶段充分利用全局搜索阶段的迭代结果建立初始Kriging 模型，并引入基于主动学习的Kriging 模型更新，借助更新后的模型提供迭代点处的预测值和梯度值，发展了基于主动学习Kriging 模型的改进一次可靠度方法，文中分析结果表明：

(1) 建议方法能够较好的处理具有隐式功能函数的结构可靠度问题，且能够在保证精度与通用一次可靠度方法一致的条件下显著提高其计算效率；

(2) 相比已有的结合Kriging 模型和一次可靠度方法的组合方法而言，建议方法对于特定的结构可靠度分析问题，其构建Kriging 模型的样本点集是唯一的，避免了可靠度分析结果的随机性，且能更好地兼顾精度、效率与收敛性。