基于增强内积矩阵的PMI 泡沫夹层结构损伤检测

田鑫海，王 乐

(西北工业大学航空学院，西安 710072)

结构损伤检测在复合材料结构的制造、服役及维护过程中发挥着重要作用[1]。聚甲基丙烯酰亚胺(polymethacrylimide, PMI)泡沫夹层复合材料结构因其质量轻、比强度高、比刚度大、易于加工等优点而被广泛应用于航空航天、交通运输、雷达天线等领域[2-5]。PMI 泡沫夹层结构作为复合材料的一种，与传统金属结构相比，在结构发生失效之前几乎不会发生变形，所以由于加工制造工艺、材料性能退化或疲劳载荷引起的结构内部损伤，如面板与PMI 泡沫的脱粘，难以及时发现，进而严重影响结构的完整性和安全性。因此，有必要发展一种对PMI 泡沫夹层结构脱粘损伤进行有效检测的方法，为保证结构可靠性、避免重大事故提供技术支持。

目前，针对PMI 泡沫A 夹层结构(面板+泡沫+面板)的传统损伤检测方法主要有[6]：用于检测面板缺陷、面板和芯材之间的脱粘以及芯材缺陷的空气耦合超声法，用于检测面板孔隙率及面板和芯材之间的脱粘的脉冲回波超声法，以及用于检测泡沫夹层结构的近表面缺陷的激光错位散斑干涉法。因泡沫本身对超声波的吸收作用，前两类基于超声的方法受泡沫性能及超声频率的严重影响，只有在特定情况下才能检测出结构损伤，而第三类方法直接受到损伤形式、加热时间以及操作人员熟练程度等因素的影响。近些年，随着太赫兹技术的发展，太赫兹无损检测技术也被用于PMI 泡沫夹层结构的损伤检测之中[7]，且相比于其他检测结果，太赫兹技术的检测结果相对理想，成像结果更清晰[8], 但太赫兹无损检测技术也刚起步，难以实现快速成像，离工程应用还有很长的路要走[9]。

近些年来，基于振动的结构损伤检测方法因其测量相对简单、容易实现在线监测等优点，在结构损伤检测领域受到国内外众多学者的广泛关注[10-16]。这类方法背后的思想是，损伤会导致结构力学性能的变化，进而体现在结构振动响应上，因此通常结合先进的数据处理方法，建立结构振动响应特征量与结构损伤状态的对应关系。通常，结构原始振动响应数据包含了丰富的结构损伤特征信息，直接对其进行加工处理不易丢失与结构损伤状态相关的信息。郑泓等[17]提出了一种基于马尔科夫状态转移向量自回归模型(MSVAR)的非线性损伤识别方法，构造信息熵作为结构损伤指标监测结构健康状态，并通过数值算例和试验验证了该方法在裂缝损伤识别中的有效性；LIU等[18]利用过桥车辆上的加速度响应信号和非线性降维技术提取结构代表性损伤特征，建立了桥梁损伤检测的诊断方法，并通过桥梁模型实验验证了所提方法的可行性；LU 和TANG[19]提出了基于自适应谐波小波变换(adaptive harmonic wavelet transform, AHWT)的方法，使用时频分析技术对兰姆波进行特征提取；左恒和郭惠勇[20]提出了基于自回归一般表达式模型和Itakura 距离的非线性损伤识别方法，并采用3 层框架非线性损伤实验验证了该方法的有效性。以上工作表明，对响应信号进行数据处理和损伤特征提取，是基于振动的结构损伤检测方法的核心。

同时，结合振动响应与数据驱动技术的结构损伤检测方法也受到了越来越多的关注。这类方法一般包括2 个步骤：通过数据处理技术构造结构损伤特征和通过分类算法实现损伤检测。构造结构损伤特征是在数据分析的基础上提取与结构损伤状态相关的损伤指标，以便降低输入数据维数和测量噪声[21-22]。在众多分类算法中，深度学习技术中的卷积神经网络(convolutional neural network,CNN)和堆栈自编码器(stack autoencoder, SAE)应用最为广泛。尤其是CNN，因其强大的特征提取能力和灵活的框架结构而广泛应用于结构损伤检测领域。LIN 等[23]提出了利用多个测点加速度响应作为深度CNN 输入的损伤定位方法，并利用仿真简支梁的损伤检测示例验证了方法的有效性；ABDELJABER等[24]提出使用一维CNN 的结构损伤快速检测系统，从原始加速度信号中自动提取最佳的损伤敏感特征，并在框架结构上验证了所提方法的性能和效率；ZHANG 等[25]提出了一种基于改进CNN的轴承故障诊断方法，将原始信号转换为二维灰度图像后进行特征提取，结果表明该方法能够满足故障检测的时效性要求；YANG 等[26]提出了基于CNN和双向门控循环单元并行的结构损伤检测模型，RASTIN 等[27]提出一种基于卷积自编码器的无监督深度学习结构损伤检测方法，他们都使用IASC-ASCE基准结构验证了所提模型和方法的有效性；TENG和CHEN[28]结合数字图像相关测量技术，提出了基于深度学习算法的渐进式结构损伤检测方法，以动态位移信号作为CNN 的训练数据，损伤识别准确率接近100%；卓德兵和曹晖[29]提出了一种结合小波时频图和轻量级卷积神经网络的螺栓连接损伤识别方法，使用声音信号进行预处理和连续小波变换得到小波时频图，以此为卷积神经网络输入识别螺栓松动。钢桁架模型的螺栓松动试验研究表明，所提方法能够准确识别不同位置、数目和程度的螺栓松动；韩淞宇等[30]提出了一种基于自适应权重和多尺度卷积的改进卷积神经网络，以提取故障样本的多尺度特征，并通过航空发动机高速轴承故障检测，验证了所提方法在不平衡数据检测中的可行性；在该领域，笔者所在团队提出了基于内积矩阵(inner product matrix,IPM)和深度学习的损伤检测方法，并通过对螺栓松动损伤的检测验证了该方法的可行性[31-32]。

虽然许多利用CNN 进行特征提取和损伤检测的方法已被提出并成功应用于不同结构的损伤检测，但依然存在以下问题值得进一步研究：

1) 损伤对激励点位置敏感，即通过有些激励点对结构进行激励难以获得有效的结构损伤特征，导致网络分类器漏检率和误判率较高。

2) 识别准确率受测点数量的影响较大，即测点的数量决定了损伤特征的质量，其数量的减少会导致识别准确率大幅下降。

针对以上不足，本文在文献[31]的基础上，提出基于增强内积矩阵(enhanced inner product matrix,EIPM)和CNN 的结构损伤检测方法，并通过PMI 泡沫A 夹层悬臂梁结构的损伤检测仿真算例及实验研究验证了所提方法的可行性和有效性。

1 理论基础

基于数据驱动的结构损伤检测方法的核心是通过数据处理技术构造损伤特征和通过分类算法实现损伤检测。因此，这里首先介绍内积矩阵和卷积神经网络的基本概念。

1.1 内积矩阵

假设结构上n个测点的加速度响应分别是a1(t),a2(t),···,an(t)，利用不同测点响应的互相关函数在时间延迟T=0时的值，组成一个n×n维的内积矩阵[31]：

式中，每一列均为参考点响应am(t)(m=1,2,···,n)和其他测点的响应作互相关函数计算得到的内积向量(inner product vector, IPV)：

式中，Rkm(0)为加速度响应ak(t)与am(t)的互相关函数在时间延迟T=0时的值，计算式如下：

式中，为向量x和y的内积。结构在白噪声激励下，利用振动响应及互相关函数的基本定义，内积向量(式(2))的理论公式如下[33]：

式中：系数 βj,r与结构的模态参数(包括固有频率、模态振型、模态阻尼、模态质量)，参考响应点的位置，白噪声激励(包括位置、个数及其双边功率谱密度)有关；φr=为第r阶模态振型。式(4)表明，在单点白噪声激励下，RIPV是由结构各阶模态振型加权叠加而成，且每一阶模态振型的加权系数均是与结构模态参数有关的常数。基于振动的结构损伤检测方法利用受监测结构的振动响应来评估其状态并识别损伤，结构的局部损伤会导致结构物理参数的改变，进而引起结构模态参数的变化，RIPV及M也会发生变化，因此M可以作为结构损伤特征应用于结构损伤检测中。

1.2 卷积神经网络

CNN 是一类包含卷积计算且具有深层结构的前馈型神经网络，通常由卷积层和池化层交替组成。与全连接网络相比，CNN 具有局部感知、权值共享、池化降维等优点，在提取重要特征的情况下，减少了训练参数的数量。

1.2.1 卷积层

卷积层(convolution layer)是CNN 的核心，主要作用是对输入的数据进行特征提取。每一层卷积层含有多个卷积核，一般认为卷积核的个数越多那么从输入数据中提取到的特征就会越丰富。从前一层l-1到当前层l的卷积运算表示如下：

1.2.2 池化层

输入数据在卷积层进行特征提取后，传入池化层(pooling layer)进行特征选择和信息过滤。这样一方面减少了可训练参数的数目，另一方面提高了网络的抗噪能力，使得对损伤特征的选择更加合理。其中常用的类型为最大池化，对于输入Xi，最大池化计算过程如下：

式中，r×r为池化窗口的尺寸，最后输出池化计算后的最大值。

1.2.3 损失函数

神经网络在训练过程中需要不断对权值和偏置进行调整，使得网络的输出值达到期望值，即实际输出值与期望值的误差最小。度量这个误差的函数称为损失函数(loss function)，针对分类问题，目前常用的损失函数为交叉熵函数：

式中：N为样本数量；M为类别数量；yik为符号函数，若样本xi的真实类别为k时取1，否则取0；p(ω,b,xik)为当前模型参数时样本xi属于类别c的预测概率。

2 结构损伤检测方法

在单点激励下，激励点位置与损伤位置之间的关系会影响结构振动响应的特征，激励点位置的选取直接决定了损伤特征的质量，进而影响损伤检测结果。因此，本文提出增强内积矩阵，被设计用来集成和融合与结构损伤相关的动力学特征。

2.1 增强内积矩阵

基于振动的结构损伤检测方法依靠多个测点采集各结构状态下的振动响应数据，分析各组响应数据之间的差异进而识别损伤。根据振动理论及相关仿真分析，若激励点位于某一损伤处附近，则该损伤附近的测点采集到的振动响应数据与无损状态下的响应数据之间的差异将会很小，导致两种状态的损伤特征差异不大，从而降低神经网络对各结构状态的识别精度。为解决以上问题，本文将单点激励增加至多点激励。

由式(4)可知，IPM 与结构的模态参数和白噪声激励有关。假设在响应的采集过程中，结构不发生突发损伤，白噪声激励的统计特性恒定不变，那么针对某一结构状态，在不同的激励位置均可以得到表征当前结构状态的不同的IPM，将不同激励点下的IPM 进行融合，可得到当前结构状态更为丰富的损伤特征——增强内积矩阵。其构造流程如图1 所示。

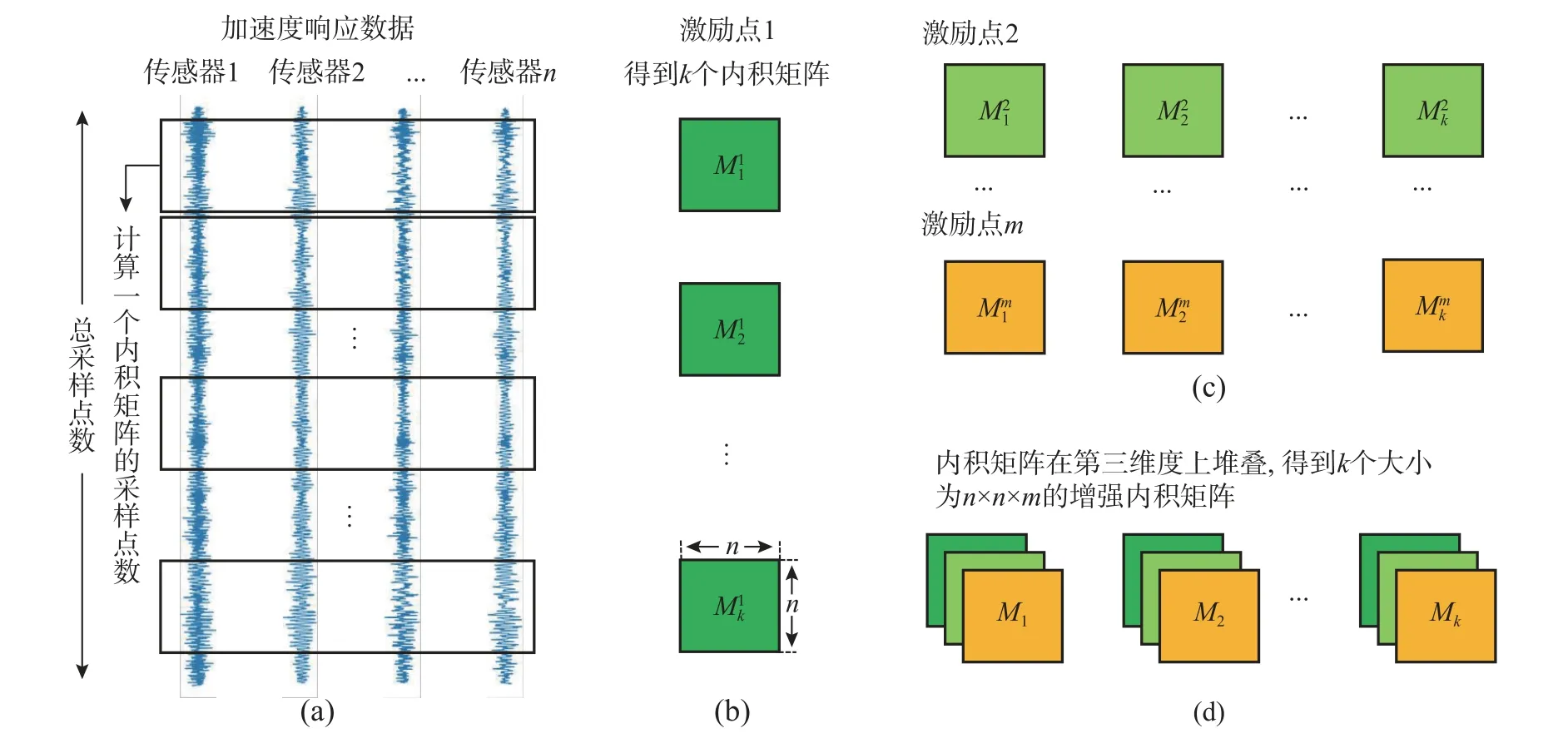
图1 增强内积矩阵构造流程Fig.1 EIPM construction process

由图1(a)～图1(d)可见，具体步骤如下：首先，任意选取被检测结构上的多个激励点分别施加白噪声激励，使用若干加速度传感器分别采集结构在各激励点下的加速度响应；然后，分别计算结构在各激励点下的IPM；最后，将各激励点下计算得到的IPM 在第三维度上进行堆叠，构造了EIPM。EIPM 是一个大小为n×n×m的三维矩阵，n和m分别代表测点及激励点的数量，每一维度上均含有与结构损伤状态相关的信息。该方法的主要思想是，生成一个包含丰富结构状态信息的损伤特征，能够更好地表征当前结构的健康状态。

2.2 卷积神经网络结构

本文提出的EIPM 是一个三维矩阵，但在第一、二维度上的维数却远小于文献[23 - 24]中使用的原始加速度响应，因此不需要大量循环堆叠卷积层与池化层进行数据降维。

本文采用的网络结构具体如表1 所示：顺序堆叠了3 层卷积层，中间没有交叉布置池化层。三层卷积层的卷积核数量依次为32、64、128，以逐渐增加特征提取能力。每层卷积核的大小均为3×3，以便提取更加具有代表性的特征。卷积步幅设置为1，每次进行卷积运算后对特征图周边进行填充处理，保持输出数据与输入数据的空间维数相同，尽可能多的保留损伤信息。通过3 层卷积运算，使得结构损伤特征更加突出；卷积层之后设置了一个批归一化层(batch normalization)和一个大小为2×2、步幅为2 的最大池化层，前者在加快网络训练和收敛速度的同时防止过拟合情况的发生，后者大大降低了网络的可训练参数；池化层之后设置了一个拉直层，将二维数据转换为一维数据，以便后续分类处理；接着是2 层全连接层，第一个全连接层有128 个神经元，第二个全连接层的数量减少至32，以整合池化层中具有类别区分性的局部信息；最后为Softmax 分类层，输出样本预测为各类别的概率。

表1 采用的CNN 结构的参数Table 1 Parameters of the adopted CNN architecture

2.3 基于EIPM 和CNN 的结构损伤检测方法

本节将提出的EIPM 与CNN 相结合应用于结构损伤检测，整个损伤检测过程如图2 所示。首先，采集结构在各结构状态不同激励点下的原始加速度响应并计算IPM，堆叠得到EIPM，将其作为样本数据库并划分为训练、验证及测试集。在输入网络之前，增强了各结构状态的损伤特征，使得各结构状态更具区分性，可以降低CNN 的学习难度，加快网络的训练及收敛速度。然后，以EIPM作为输入训练CNN 模型，逐层进行损伤特征再提取和学习，通过最小化预测标签和真实标签之间的交叉熵损失函数，反向传播优化网络每一层的参数。最后，将测试数据输入训练完成后的CNN模型，进行结构损伤状态的检测并可视化结果。

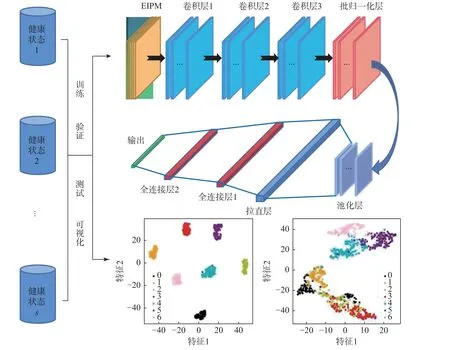
图2 结构损伤检测流程Fig.2 Structural damage detection process

3 仿真算例

PMI 泡沫夹层结构现已成功应用于航空航天等领域，其在制造和服役过程中不可避免地会受到加工工艺和冲击载荷的影响而发生损伤，尤其是面板与芯材之间的脱粘损伤，这种损伤难以从外观上目视检测，从而带来严重的安全隐患。本节通过对PMI 泡沫A 夹层悬臂梁结构面板与芯材之间的脱粘损伤进行检测，来验证所提结构损伤检测方法的可行性。

本文建立的PMI 泡沫A 夹层悬臂梁模型如图3所示，几何尺寸为320 mm×40 mm×6.55 mm。夹层结构的上、下面板为层合结构，材料为石英纤维和乙烯基树脂(弹性模量E11=24 GPa，E22=21 GPa，密度ρ=1537.76 kg/m3，泊松比ν12=0.18，剪切模量G12=G13=3.5 GPa)，其铺层方式与各层厚度如表2 所示。PMI 泡沫芯材的弹性模量、密度和泊松比分别为75 MPa 、75 kg/m3、0.3。

表2 铺层方式及各层厚度Table 2 Laminating method and thickness of each layer

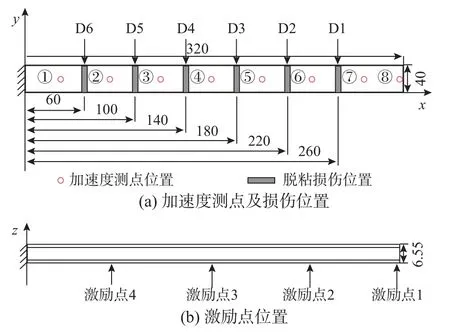
图3 PMI 泡沫夹层结构模型 /mmFig.3 Model of PMI foam sandwich structure

在仿真中一共模拟了7 种结构状态，包括1 种完好状态和6 种损伤状态，将其分别命名为U、D1、···、D6，其中 D1发生在距夹持端260 mm 处，D2 ～D6 距 D1的距离以40 mm 为间隔减少，每处损伤均设置为宽度为10 mm 的贯穿脱粘损伤。针对每一种结构状态，以40 mm 为间隔在悬臂梁模型中心轴线上设置了8 个加速度测点，如图3(a)所示。以20 kHz 的采样频率采集结构在单点白噪声激励下指定测点的加速度响应，采样时间为60 s，即采样点数为1.2×106个。根据EIPM 的构造方法，原则上可以在结构上任意选取激励点的位置，为简便，本文分别选取悬臂梁结构自由端、距自由端1/4处、2/4处和3/4处中轴线上的点作为激励点对结构施加白噪声激励，如图3(b)所示。

对每种结构状态分别进行了4 次随机激励，共获得28 组数据，每组数据由8 个测点的加速度响应数据组成。对每组数据，取各测点同一时间段的1024 个采样点计算得到1 个IPM，每种结构状态在每个激励点下取1024 个IPM，再将4 个激励点在同一时间段计算得到的IPM 在第三维度上堆叠，那么每种结构状态有1024 个EIPM，即1024 个数据样本。7 种结构状态共有7168 个数据样本构成样本数据库，将它们以8∶1∶1 的比例用于CNN 模型的训练、验证和测试。

3.1 结果与分析

基于振动的结构损伤检测方法通过分析多个测点采集的结构振动响应中含有的损伤信息完成对损伤的检测。通常，测点数量越多，响应数据中含有的损伤信息就越丰富，损伤特征就越显著，对结构损伤的识别准确率就越高。然而，在实际结构中通常难以布置足够多的测点。为检验所提方法的稳定性，本节将测点数量分别减少至6 个、4 个、3 个和2 个。为了使测点减少后的分布尽可能均匀，针对6 个测点，取①、②、④、⑤、⑦、⑧号测点；针对4 个测点，取①、③、⑤、⑦号测点；针对3 个测点，取②、④、⑥号测点；针对2 个测点，取③、⑥号测点。作为对比，单点激励下的IPM 也将作为CNN 模型的输入(即IPM 法)对PMI 泡沫夹层悬臂梁的损伤进行检测。

表3 给出了EIPM 法和IPM 法在不同测点数量下对测试集的平均识别准确率及损失函数值。可以看出：不同激励点下利用IPM 法的识别准确率不尽相同，说明结构损伤对激励点位置敏感，不同激励点下的结构振动响应计算得到的损伤特征不同；EIPM 法在不同测点数量下均能较好地识别损伤，尤其是在3 个测点及以上时，平均识别准确率均在99%以上，在2 个测点时也能达到81.31%的识别准确率。IPM 法在8 个测点时的准确率与EIPM 法均达到了100.00%，但EIPM 法的损失函数值远低于IPM 法，说明本文构造的EIPM 更易于CNN模型的学习。随着测点数量的减少，IPM 法的平均识别准确率迅速降低，尤其是激励点1 和激励点3，当测点数减少为4 个时，其平均识别准确率分别降低至59.83%和71.26%，受测点数量减少的影响较大。分析这一现象的原因，主要是减少测点后与结构状态相关的损伤信息也随之减少，使得表征各结构状态的损伤特征不显著，网络无法学习到足够的具有类别区分性的特征，导致各结构状态互相混淆识别，识别准确率下降。对比IPM，EIPM 表现出了较好的稳定性，说明EIPM受测点数量减少的影响较小，可在较少测点下识别PMI 泡沫夹层结构的脱粘损伤。

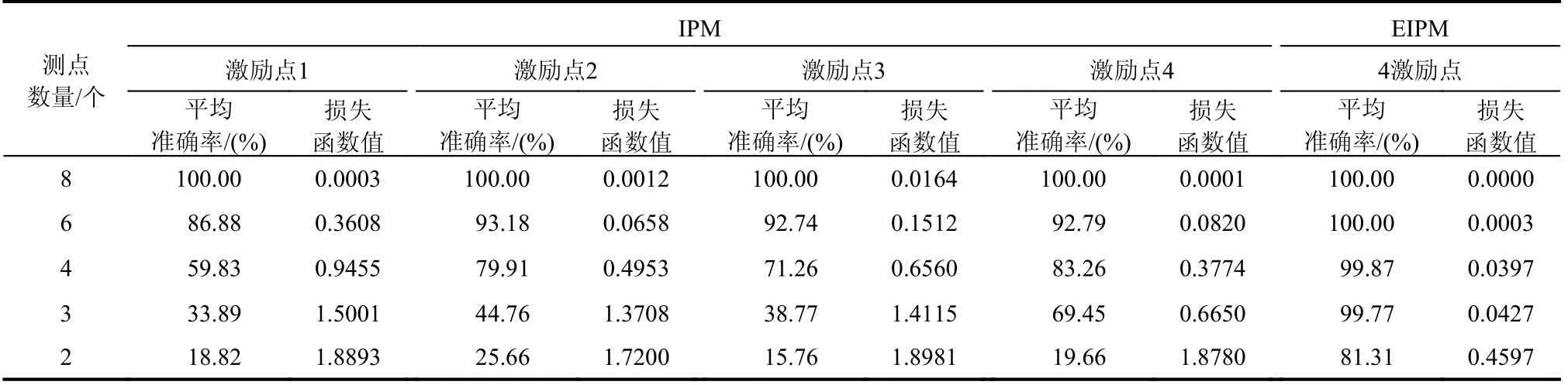
表3 不同测点数量下的平均识别准确率与损失函数值Table 3 Average recognition accuracy and loss function value for different number of measuring points

平均识别准确率反映了网络的整体识别性能，并不能反映对各结构状态的识别效果。而精确率和召回率是针对每种结构状态的评价指标，与之对应的分别是误判率和漏检率。因此，以6个测点的识别结果为例，图4 给出了EIPM 法及IPM 法对7 种结构状态的识别精度和召回率。从图4(a)可以看出，IPM 法对U状态的识别精度均降低至80%以下，即20%以上的无损状态会被错误识别为损伤状态，并且对D1～D6状态也会发生不同程度的误判；而EIPM 法对各结构状态的识别精度均为100%，表现出很好的稳定性。从图4(b)可以看出，IPM 法对各结构状态会发生不同程度的漏检，不能准确地检测出结构的损伤位置，这是由于减少测点数量后，损伤特征中含有的损伤信息减少，各结构状态的损伤特征不明显，导致漏检率增大；而EIPM 法对各结构状态的召回率均为100%，即没有出现漏检情况，表现出很好的可靠性。

图4 EIPM 法与IPM 法对7 种结构状态的评价指标比较Fig.4 Comparison of EIPM method and IPM method on the evaluation indicators of seven structural states

为了说明不同方法在识别准确率相同时的训练收敛速度，图5 给出了EIPM 法与IPM 法在8个测点时对验证集的平均识别准确率与损失函数随训练迭代次数的变化曲线。结果表明，虽然各方法的最终识别准确率均为100%，但网络的迭代收敛速度各不相同，EIPM 法的收敛速度明显大于IPM 法，说明EIPM 可以拓展IPM 中含有的损伤信息，使得构造的损伤特征更加显著，加速CNN进行特征再提取并学习具有类别区分性的特征。

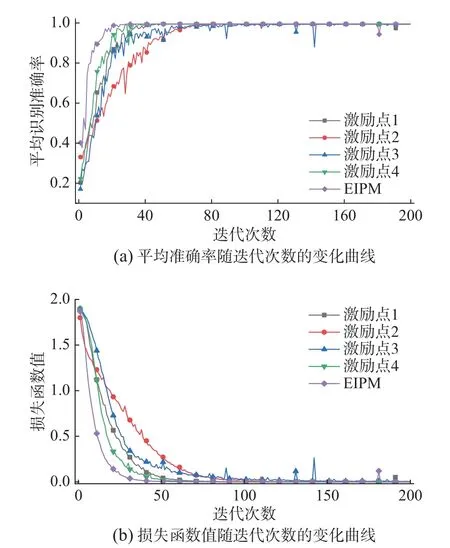
图5 网络训练过程(8 个测点)Fig.5 Training process of network (8 measuring points)

图6 给出了EIPM 法在不同测点数量下对验证集的平均识别准确率与损失函数值的变化曲线。从结果可以看出，测点数量的减少会影响网络的迭代收敛速度，因为网络需要从较少的损伤信息中提取与结构当前状态相关的信息，使得特征学习变得困难。但结合表3 分析可知，在3 个测点以上时，所提方法的最终识别准确率均达到99%上，远高于IPM 法。

图6 EIPM 法的网络训练过程Fig.6 Training process of network for EIPM method

综合分析上述结果可知，本文提出的EIPM 方法可融合不同激励点下得到的损伤信息，增强各测点响应数据的相关性，进而得到各结构状态增强后的损伤特征，以EIPM 作为网络的输入更利于CNN 模型的特征再提取和学习，使得网络的收敛速度更快，识别准确率更高。与IPM 法相比，EIPM法表现出更好的稳定性和可靠性。

3.2 数据量的影响

在基于数据驱动的结构损伤检测领域，一般认为，数据量越大，经过网络充分学习后输出的结果就越好。EIPM 集成并融合了各激励点下得到的IPM，其数据量相当于IPM 的4 倍。为消除数据量在各方法对比中带来的不平衡性，本节将每个激励点分别进行4 次白噪声激励，并将每次激励下得到的IPM 在第三维度进行堆叠，构造与EIPM具有相同层次结构的三维矩阵，即EIPM 法和IPM法的网络输入均为大小为n×n×4的三维矩阵。

将单点单次激励增加至单点多次激励后，从表4 可以看出：IPM 法采用6 个测点时，准确率稍有提升(提升5%至10%)；采用4 个和3 个测点时，准确率显著提升(提升4%至20%)；采用2 个测点时，准确率也略有提升。结果表明，单点激励的次数对IPM 法的识别准确率有一定的影响，多次激励得到的IPM 堆叠为三维矩阵后增加了损伤特征中含有的数据量，网络的识别准确率随之提升。但IPM 法的识别准确率在测点数量为4 个及以下时仍远低于EIPM 法，分析这一现象出现的原因，主要是EIPM 是由各激励点下的IPM 在第三维度上堆叠拓展而成，不同激励点下的IPM 表征着结构当前状态的不同的损伤特征，所以EIPM各通道上的损伤信息不尽相同。EIPM 输入CNN后，卷积层对各通道上的损伤信息进行特征再提取和融合，使得网络提取到的损伤特征更能代表结构当前的损伤状态，识别准确率更高。对于IPM 法，虽然增加了激励次数，但每一次激励均在同一点，IPM 中的损伤信息大多相同，无法为网络带来更多的损伤信息，所以单点多次激励仅仅在数据量层面提升了识别准确率，没有增加新的损伤信息。

表4 相同数据量下的平均识别准确率与损失函数值Table 4 Average recognition accuracy and loss function value for the same amount of data

上述分析结果表明，本文提出的EIPM 方法可以集成并融合多个激励点下与结构状态相关的损伤信息，为网络提供具有鉴别性的损伤特征输入，即使在少量测点下也能获得不错的识别准确率，较传统的IPM 方法更具有稳定性。

4 实验验证

4.1 实验设置

本节将采用PMI 泡沫A 夹层悬臂梁结构的脱粘损伤检测来验证本文所提方法的有效性。PMI泡沫A 夹层悬臂梁的实验段几何尺寸及材料属性与仿真算例保持一致，固支端由宽度为20 mm、厚度为30 mm、长度为200 mm 的钢块固定于水平台上。

实验采用0 kHz～2 kHz 的带通白噪声作为激励，采集加速度响应信号构造EIPM，进而对结构的脱粘损伤进行检测。激励点位置及测点布置均与仿真算例保持一致。实验现场布置如图7 所示，使用LMS Test.Lab 试验分析软件生成带通白噪声激励，驱动非接触式电磁激振器激励悬臂梁，利用LMS SCADAS Mobile 移动式数据采集装置和PCB Piezoelectrics 333B30 加速度传感器对悬臂梁指定测点的加速度响应信号进行采集。

图7 实验现场及局部脱粘损伤Fig.7 Experimental site and local debonding damage

实验中共模拟了7 种结构状态，包括1 种完好状态和6 种损伤状态。由于更换实验件不可避免地会带来实验件原始状态及边界条件的细微变化，为避免这一变化给实验件带来除损伤之外的新的变量，本节将在同一实验件上以损伤累加的形式模拟不同的结构损伤状态，如表5 所示。为消除数据量带来的不平衡问题，本节依然对同一个激励点进行4 次白噪声激励，使得EIPM 法与IPM法的网络输入大小均为n×n×4。针对每一种结构状态，采用20 kHz 的采样频率采集加速度响应信号，采样时间为60 s。

表5 损伤状态设置Table 5 Damage state settings

4.2 实验结果分析

表6 给出了EIPM 法与IPM 法在不同测点数量下对测试集的平均识别准确率与损失函数值。从中可以看出：1) 得到了与仿真算例结果相同的规律，即不同激励点下的识别准确率和损失函数值各不相同，这表明在不同的激励点下会生成不同的损伤特征；2) 随着测点数量的减少，IPM法的识别准确率降低、损失函数值增大，说明IPM 法受测点数量减少的影响较大，无法在少量测点下准确构造与结构状态相关的损伤特征，而EIPM 法克服了这一不足之处，通过融合各激励下生成的IPM，能够较为准确地表征出结构当前状态的损伤特征；3) 比较表4 和表6 可以发现，实验结果优于仿真结果。分析其原因，主要是实验中的损伤是以累加的形式模拟的，损伤累加得越多，对结构的模态参数影响越大，所以IPM 中的损伤特征就越显著，那么网络的识别准确率就随之增加。

为了直观展示各方法对各结构状态的识别性能，采用T-SNE(T-distributed stochastic neighbor embedding)降维技术可视化3 个测点时网络对测试集样本的识别结果，如图8 所示。结果显示，EIPM法与IPM 法相比，类间距更大，类内间距更小，即EIPM 法更容易使得同一类别的样本彼此靠近。结果表明，EIPM 使得各个结构状态的损伤特征更加显著，网络更容易区分各个结构损伤状态，最后实现高准确率的损伤识别。

图8 3 个测点时各方法输出层T-SNE 可视化结果Fig.8 T-SNE visualization results of the output layer of each method at 3 measuring points

4.3 数据量的影响

对于文献[30]中所提出的IPM 方法，计算一个IPM 所使用的采样点数及每种结构状态的IPM 数量均会影响最后的识别准确率。本节将数据量降低1/2，即分别使用512 个采样点计算一个IPM、每种结构状态取1024 个IPM，简称为构造方式1；1024 个采样点计算一个IPM、每种结构状态取512 个IPM，简称为构造方式2。使用以上两种方式构建样本数据库分别训练CNN 模型，研究采样点数和样本数对各方法的影响。

识别结果如表7 和表8 所示，可以看出：数据量减少1/2 后，IPM 法在3 个、4 个测点时的识别准确率均有明显的下降，这是因为减少数据量的同时减少测点数量，使得损伤特征中的损伤信息变得更少，网络难以从较少的损伤信息中提取到足够的具有类别区分性的特征，而EIPM 法在3 个测点时的识别准确率依然有93.8%和96.7%，远高于IPM 法；分别降低采样点数和IPM 数量对平均识别准确率的影响程度各不相同，降低采样点数对平均识别准确率的影响更大，这是因为计算IPM 的采样点数直接决定了构造的损伤特征的质量，降低采样点数导致各结构状态的损伤特征区分度下降，识别准确率降低。

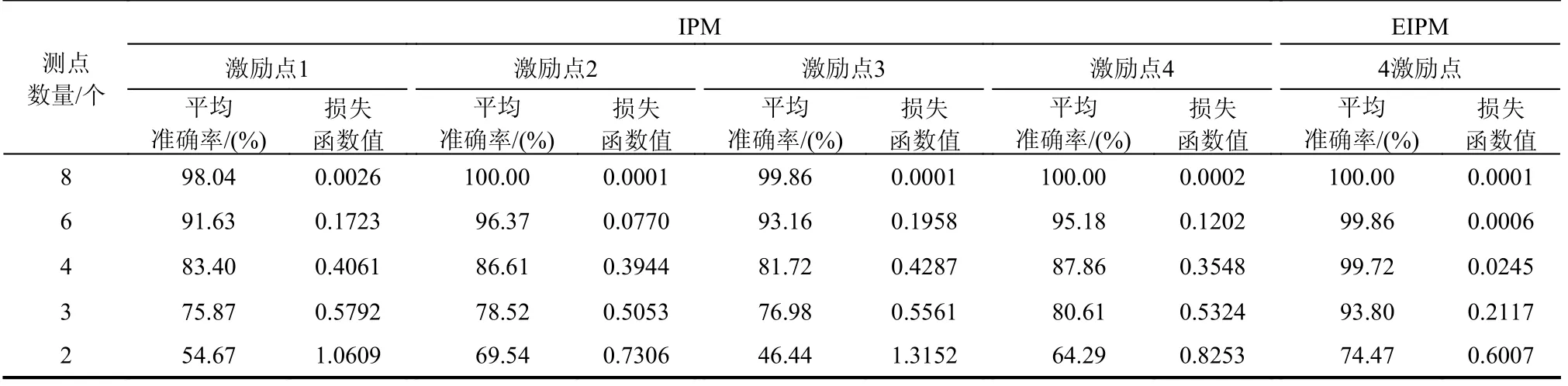
表7 构造方式1 下各方法的识别结果Table 7 The identification results of each method under construction mode 1

表8 构造方式2 下各方法的识别结果Table 8 The identification results of each method under construction mode 2

上述研究结果表明：损伤特征的质量比样本数量更重要，一个较优的损伤特征能使网络对各结构状态的识别准确率更高，即该损伤特征含有更多的损伤信息，更能表征结构当前的损伤状态。本文提出的EIPM 可融合各激励点下的损伤特征，仅利用3 个测点下的少量数据，便可有效识别PMI 泡沫夹层悬臂梁结构的各个损伤状态。

5 结论

本文以IPM 为基础，利用四个激励点的加速度响应数据分别计算得到IPM，并将各激励点在同一时间段计算得到的IPM 在第三维度进行堆叠，得到EIPM，以此作为CNN 的输入，结构损伤状态为输出，提出了基于EIPM 和CNN 的结构损伤检测方法。利用PMI 泡沫A 夹层悬臂梁结构的仿真算例和实验，验证了所提方法的可行性和有效性，得到以下主要结论：

(1) EIPM 可以集成并融合不同激励点下的损伤特征，有效解决损伤对激励点位置敏感、单次激励得到的损伤特征不佳的问题，使得表征结构状态的损伤特征更加显著。与IPM 相比，EIPM更利于CNN 模型学习到具有类别区分性的特征，网络的收敛速度更快，识别准确率更高。

(2) EIPM 能够有效解决测点数量减少后识别准确率大幅降低的问题。仿真算例和实验测试结果均表明，仅使用3 个测点的加速度响应信号就能达到99%以上的平均识别准确率，远高于基于IPM 的损伤检测方法，更具稳定性。

(3) 总数据量的减少对所提方法的影响不大。在同等数据量时，损伤特征的质量比样本数量更重要，一个较优的损伤特征能使网络对各结构状态的识别准确率更高。

(4) 结构损伤必然会导致结构模态参数以及IPM 的改变，定性分析可知，EIPM 方法仍然适用于复合材料层合板的分层损伤检测，但如何区分同一位置不同层的分层损伤是后续研究的一个重点。