基于新的改进Bouc-Wen 模型的预制RC 桥墩滞回模型研究
徐亚洲,魏克伦,丁艳琼
(西安建筑科技大学土木工程学院,陕西,西安 710055)
钢筋混凝土桥墩在强震作用下通常会表现出明显的强度退化、刚度退化和捏缩效应等非线性滞回特性。建立能够反映钢筋混凝土桥墩滞回特性的非线性滞回模型,是准确、有效地预测其在强震作用下地震响应的基础[1]。
目前,研究人员已经提出了多种可以用来模拟非线性滞回性能的滞回模型。根据光滑程度,这些滞回模型可以分为折线型滞回模型和光滑型滞回模型[2]。折线型滞回模型采用线段直观描述滞回曲线的加卸载规律,如Clough 模型[3]、Takeda模型[4]等。折线型滞回模型虽然相对简单,但是存在刚度变化不连续、程序实现不方便等缺点。相比之下,光滑型滞回模型的刚度变化连续且易于程序化[2]。BOUC[5]首先提出了用微分形式的数学模型来模拟滞回非线性系统,即Bouc 模型,但该模型不能考虑强度退化、刚度退化和捏缩效应。WEN[6]通过对原有的Bouc 模型进行改进,建立了用于结构随机振动分析的光滑型滞回模型,称为Bouc-Wen 模型。BABER 和WEN[7]通过引入刚度退化和强度退化参数改进了Bouc-Wen 模型,其中刚度退化和强度退化参数通过累积滞回耗能准则定义,并广泛应用于磁流变阻尼器[8]、消能减震结构[9]、阻尼耗能支撑[10]等。该模型虽然可以考虑刚度和强度的退化,但是不能模拟捏缩效应。
鉴于此,BABER 和NOORI[11]以考虑刚度、强度退化的Bouc-Wen 模型为基础,通过构建含有6 个参数的“捏缩效应”函数提出了改进Bouc-Wen 模型,称为Bouc-Wen-Baber-Noori(BWBN)模型。该模型能综合考虑非线性系统的滞回性能,包括强度退化、刚度退化和捏缩效应等。余波等[12]采用BWBN 模型,结合微分进化算法研究了钢筋混凝土柱的恢复力模型。韩强等[13]运用无迹卡尔曼滤波(UKF)对BWBN 模型进行参数识别,建立了钢筋混凝土桥墩的滞回模型。郭秀秀等[14]基于BWBN 模型建立了木排架结构的恢复力模型,并以此为基础研究了木排架结构在强震作用下的地震响应。上述研究成果表明:BWBN 模型已广泛应用于非线性系统的滞回性能模拟。但是BWBN模型也存在函数复杂、参数太多的问题,导致其计算效率较低。因此,有必要在Bouc-wen 模型的基础上,提出一种计算效率更高的光滑型滞回模型。
本文基于近似狄拉克δ函数构建更简单、高效的“捏缩效应”函数,进而提出了一种新的改进Bouc-Wen(MBW)模型。与BWBN 模型相比,MBW模型需要识别的参数更少。本文基于预制RC 桥墩的拟静力试验数据,利用MATLAB 遗传算法工具箱对BWBN 模型和MBW 模型进行参数识别。结果表明:本文提出的MBW 模型能够很好地模拟预制RC 桥墩在往复荷载作用下的滞回性能,并具有更高的计算精度。
1 Bouc-Wen-Baber-Noori 模型
Bouc-Wen-Baber-Noori(BWBN)模型是以考虑刚度、强度退化的Bouc-Wen 模型为基础,通过构建含有6 个参数的“捏缩效应”函数来实现捏缩效应。BWBN 模型可以较好模拟钢筋混凝土结构的滞回性能,包括强度退化、刚度退化和捏缩效应等[15-19]。
基于BWBN 模型,预制RC 桥墩的恢复力可以表示为:
式中:F(u,z)为桥墩恢复力;k0为初始线弹性刚度; α为屈服后刚度比;u为桥墩顶部位移;z为滞回位移。
桥墩顶部位移u与滞回位移z之间的关系为:
式中:A、 β 、 γ和n为控制滞回曲线形状的模型参数; δη和 δν分别为控制滞回曲线刚度退化和强度退化的模型参数; ε为累积滞回耗能;h(z)为“捏缩效应”函数,可以表示为:
本文用MATLAB 编程实现了BWBN 模型,分别研究了控制捏缩效应的模型参数对滞回曲线的影响,如图1~图6 所示。参数q控制捏缩效应的开始。参数p主要控制捏缩效应的捏缩斜率。参数ζs控制总滑移量。参数 ψ 、 δψ和 λ对滞回曲线的影响基本一致,随着参数 ψ 、 δψ和 λ的增大,滞回曲线的捏缩量逐渐增大,捏缩效应越来越强烈,可以认为参数 ψ 、 δψ和λ共同控制滞回曲线的总捏缩量。
综上所述,滞回曲线的捏缩效应由4 个因素控制:捏缩效应的开始、捏缩斜率、总滑移量和总捏缩量。同时,由图4~图6 可知,参数 ψ、δψ和 λ对滞回曲线的作用相似,说明BWBN 模型存在功能冗余,具有进一步优化的空间。
2 新的改进Bouc-Wen 模型
本文提出的改进Bouc-Wen (MBW)模型的恢复力表达式与BWBN 模型的恢复力表达式一致,如式(1)所示。与BWBN 模型的不同之处在于,MBW 模型采用更简单、高效“捏缩效应”函数来实现捏缩效应。MBW 模型中,桥墩顶部位移u与滞回位移z之间的关系如式(10)所示:
式中:u为桥墩顶部位移;z为滞回位移;A、 β、γ和n控制滞回曲线形状的模型参数; η和ν分别控制滞回曲线的刚度退化和强度退化,其计算公式见式(3)和式(4)。h(u,ε)为新的“捏缩效应”函数,可以表示为:
式中: ρ 、 θ、φ和τ为控制捏缩效应的模型参数;ε为累积滞回耗能。
“捏缩效应”函数h(u,ε)对滞回曲线的影响如图7 所示。

图7 “捏缩效应”函数对滞回曲线的影响Fig.7 Effect of pinching function on hysteretic curve
当h(u,ε)=1,滞回模型为不考虑捏缩效应的Bouc-Wen 光滑模型,如图7(a)所示。
“捏缩效应”函数h(u,ε)的函数形状为U 形,如图7(b)所示。在原点附近为函数曲线平直,函数值最小;两侧是光滑曲线,随着远离原点其函数值逐渐增大,而斜率逐渐减小。
“捏缩效应”函数(图7(b))通过控制Bouc-Wen 光滑模型(图7(a))滞回位移z的变化来实现捏缩效应,得到考虑捏缩效应的MBW 模型滞回曲线,如图7(c)所示。由式(10)可知,在原点附近“捏缩效应”函数h(u,ε)可以通过函数值的降低直接减小滞回位移z。又由式(1)可知,滞回位移z的减小会直接降低恢复力F(u,z),由此实现滞回曲线在原点附近的捏缩。
2.1 “捏缩效应”函数
本文提出的改进Bouc-Wen (MBW)模型,创新之处在于基于近似狄拉克δ函数[20]构建一个更简单、高效的“捏缩效应”函数h(u,ε)。该函数只有4 个参数,每个参数都有明确的物理意义。MBW模型的“捏缩效应”函数h(u,ε)分3 步构建,如图8所示。
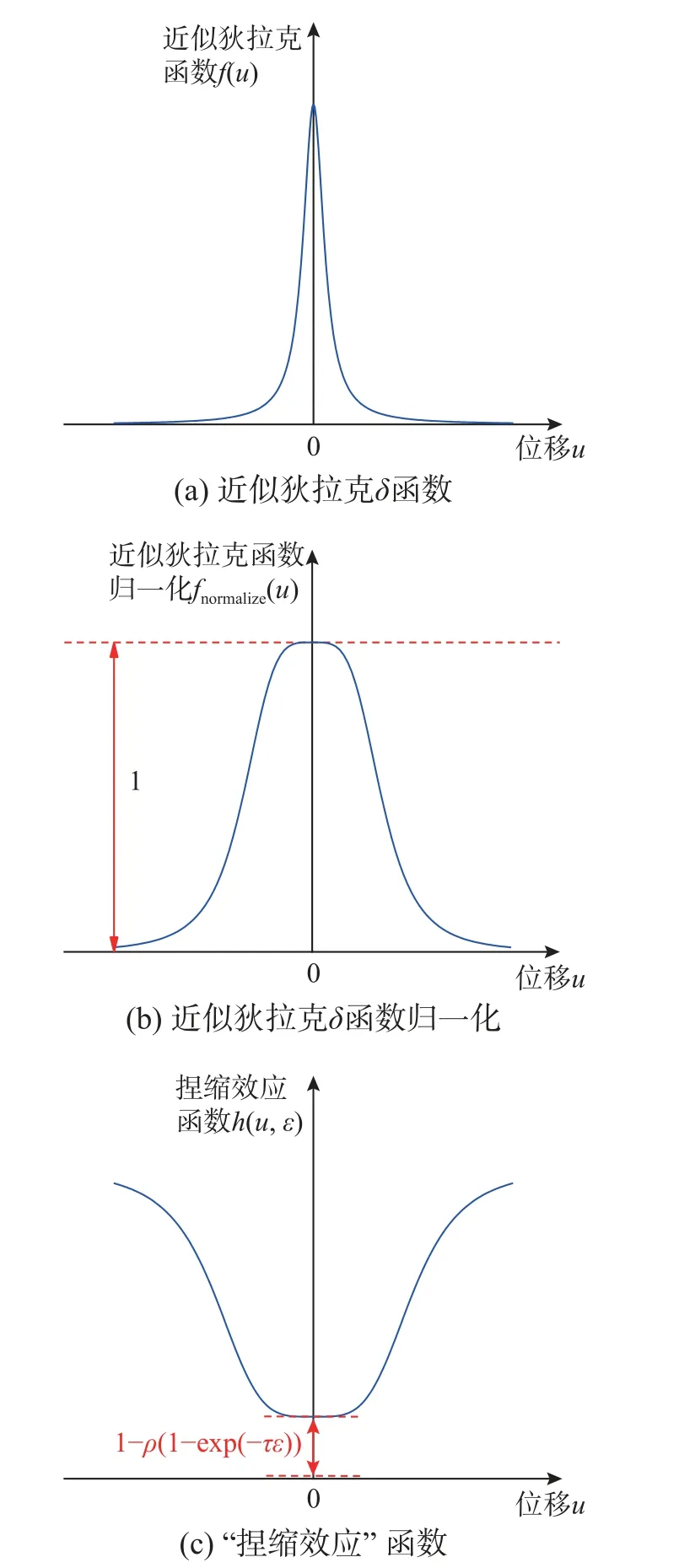
图8 “捏缩效应”函数的构建过程Fig.8 Process of constructing the pinching function
1) 构建近似狄拉克δ函数f(u)。
式中:u为桥墩顶部位移;φ和θ为“捏缩效应”函数的参数。参数φ的建议取值范围为[0,umax],参数θ的建议取值范围为[2, 8]。其中u取绝对值是为了保证参数 θ可以取值连续,从而使基于函数f(u)构造的“捏缩效应”函数更加精确。
近似狄拉克 δ函数f(u)如图8(a)所示。函数f(u)在原点附近急剧增加,并在原点处达到最大值;在远离原点的地方,函数f(u)基本为0。
2) 进行近似狄拉克δ函数f(u)归一化[21],得到fn(u)。
函数fn(u)如图8(b)所示。函数的最大值为1,函数形状为倒U 形,顶部为平直区,两侧是光滑曲线,其斜率随着远离原点而逐渐减小。
3) 构建“捏缩效应”函数h(u,ε)。
在式(13)的基础上构建“捏缩效应”函数h(u,ε),如式(11)所示。
图8(c)模拟了单个滞回环中函数h(u,ε)随u变化的规律。为了便于研究,不考虑累积滞回耗能ε的变化。
如图8(c)所示,在单个滞回环中,当u=0,“捏缩效应”函数值最小,h(0,ε)=1-ρ(1-exp(-τε)),此时“捏缩效应”函数h(u,ε)在该滞回环中引起的捏缩效应最强。
参数 θ和φ对“捏缩效应”函数的影响如图9所示。从图9(a)中可以看出,随着参数θ的增大,函数曲线两侧的斜率逐渐变大,曲线越来越陡。从图9(b)可以看出,随着参数φ的增大,函数曲线顶部平直区的宽度逐渐增加。
本文基于加载过程中累积滞回耗能ε的变化来考虑捏缩效应的发展。由图8(c)可知,h(0,ε)可以衡量试验加载过程中各个滞回环的捏缩幅度。
根据某现浇桥墩的拟静力试验数据,得到累积滞回耗能ε随滞回环数的变化曲线。并以此为基础,研究了在试验加载中各个滞回环中h(0,ε)随着累积滞回耗能ε增加的变化规律,如图10 所示。
由图10 可以看出,在试验加载中h(0,ε)的变化可以分为3 个阶段:1) 在试验初期,试件处于弹性阶段,累积滞回耗能 ε很低,此时h(0,ε)的值近似等于1,滞回曲线不发生捏缩效应;2) 随着试件进入塑性阶段,累积滞回耗能ε逐渐增加,此时h(0,ε)的值逐渐减小,滞回曲线开始出现捏缩效应并逐渐加强; 3) 当累积滞回耗能 ε增大到一定水平时,h(0,ε)的值下降到1-ρ,并保持恒定,此时滞回曲线捏缩效应最强,同时捏缩量达到整个试验加载中的最大值。
由图10(a)可以看出,参数 ρ控制总捏缩量,随着参数 ρ的增加,总捏缩量呈现线性增加。由图10(b)可以看出,参数τ控制捏缩效应的开始。随着参数τ的增大,捏缩效应开始的时间越来越早,捏缩效应的发展速率越来越快。
2.2 控制捏缩效应的模型参数对滞回曲线的影响
本文用MATLAB 编程实现了MBW 模型,分别研究了控制捏缩效应的模型参数对滞回曲线的影响,如图11~图14 所示。
从图11 可以看出,参数 ρ控制着总捏缩量。随着参数 ρ的增大,捏缩量逐渐增大。从图12 可以看出,参数θ控制滞回曲线的捏缩斜率。随着参数θ的增大,滞回曲线变得越来越陡,斜率逐渐增大。从图13 可以看出,参数φ控制滞回曲线的总滑移量。随着参数φ的增大,滞回曲线滑移区的宽度逐渐增大,同时捏缩量也逐渐增加。由图14 可知,参数τ控制着捏缩效应的开始。随着参数τ值的增大,捏缩效应的发展速率逐渐增大,捏缩效应出现的时间越来越早。
由图11~图14 可知,MBW 模型的“捏缩效应”函数能够有效地模拟捏缩效应。“捏缩效应”函数的各个参数都具有明确的物理意义,同时参数之间也存在相互影响。
值得注意的是,BWBN 模型的“捏缩效应”函数是一个包含6 个参数的非常复杂的函数,如式(6)~式(9)所示。而MBW 模型的“捏缩效应”函数只包含4 个模型参数,函数表达式也更简单明了,如式(11)所示。
综上所述,与BWBN 模型相比,MBW 模型“捏缩效应”函数的参数更少,同时其简洁的函数表达式也更有利于程序化和提高计算效率。
3 模型验证
3.1 参数识别
BWBN 模型和MBW 模型中参数的作用如表1和表2 所示,BWBN 模型包括14 个模型参数(k0、 α、A、 β 、 γ、n、 δη、 δν、q、p、 ζs、 ψ 、δψ和 λ),而MBW 模型包括12 个模型参数(k0、 α、A、 β 、 γ、n、 δη、 δν、φ、 θ 、 ρ和τ)。BWBN 模型和MBW 模型的参数较多,同时参数之间相互影响,无法直接通过计算公式确定模型参数的准确值。

表1 BWBN 模型参数[12]Table 1 BWBN model parameters[12]
表2 MBW 模型参数Table 2 MBW model parameters
本文利用MATLAB 遗传算法工具箱[22]进行参数识别。滞回模型的参数识别过程为优化问题,通过寻找最优的模型参数使得目标函数值最小。其中,目标函数为滞回模型计算得到的恢复力预测值与恢复力试验值之间的误差,可以表示为[12]:
本文参数识别过程中,MATLAB 遗传算法工具箱的设置为,种群个数100 个,迭代代数100 代。
3.2 模型验证算例
本文选取的预制RC 桥墩试验数据为西安建筑科技大学徐亚洲等[23]于2021 年所做的螺纹钢法兰连接预制装配桥墩拟静力试验,包括一个现浇试件(CIP)和两个预制试件(PC1 和PC2),试件参数见表3,具体试验方案见文献[23]。利用MATLAB遗传算法工具箱,对BWBN 模型和MBW 模型进行参数识别,并结合试验结果对BWBN 模型和MBW模型的数值模拟结果进行对比分析。
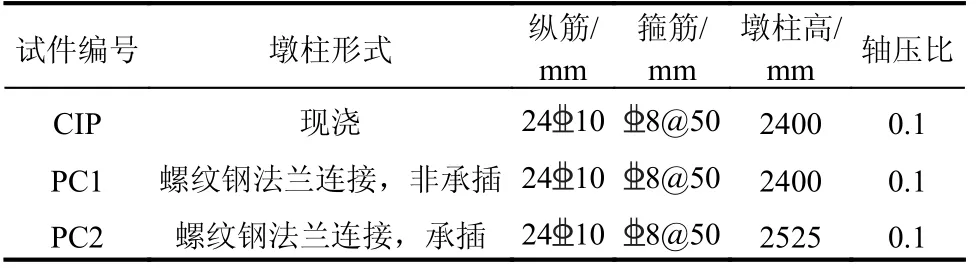
表3 试件参数Table 3 Details of specimens
CIP 试件、PC1 试件和PC2 试件滞回模型的初始线弹性刚度k0,通过拟静力试验数据计算得到:21.56 kN/mm、15.23 kN/mm 和20.19 kN/mm。
CIP 试件、PC1 试件和PC2 试件的BWBN 模型第100 代的参数识别结果见表4,MBW 模型第100 代的参数识别结果见表5。表6 显示了BWBN模型和MBW 模型的数值模拟结果与试验结果之间的误差。

表4 BWBN 模型参数识别结果Table 4 Parameter identification results of BWBN model

表5 MBW 模型参数识别结果Table 5 Parameter identification results of MBW model

表6 试验结果与滞回模型之间的误差Table 6 Error between test results and hysteretic model
图15 显示了三个桥墩试件在参数识别过程的目标函数值随进化代数变化的轨迹,图中水平参考线(虚线)为BWBN 模型第100 代目标函数值。从图15 可见,CIP 试件、PC1 试件和PC2 试件的MBW 模型分别在第15 代、34 代和16 代达到BWBN 模型第100 代目标函数值,表明参数识别过程中MBW 模型需要的进化代数降低了66%以上,具有更高的计算效率。参数识别过程中第100 代的目标函数值见表6。从表6 中可见,MBW 模型具有更高计算精度。

图15 目标函数值随进化代数变化的轨迹Fig.15 Trace of objective function values along with evolutionary generations
图16 将BWBN 模型和MBW 模型模拟的滞回曲线与试验数据进行对比分析。从图16 可以看出,MBW 模型模拟的滞回曲线与试验数据吻合更好。调用Matlab 中的corrcoef 函数,计算得到BWBN 模型和MBW 模型模拟的恢复力预测值与恢复力试验值之间的相关性系数见表6。结果表明:MBW 模型模拟的滞回曲线与试验数据具有更高的相关性。
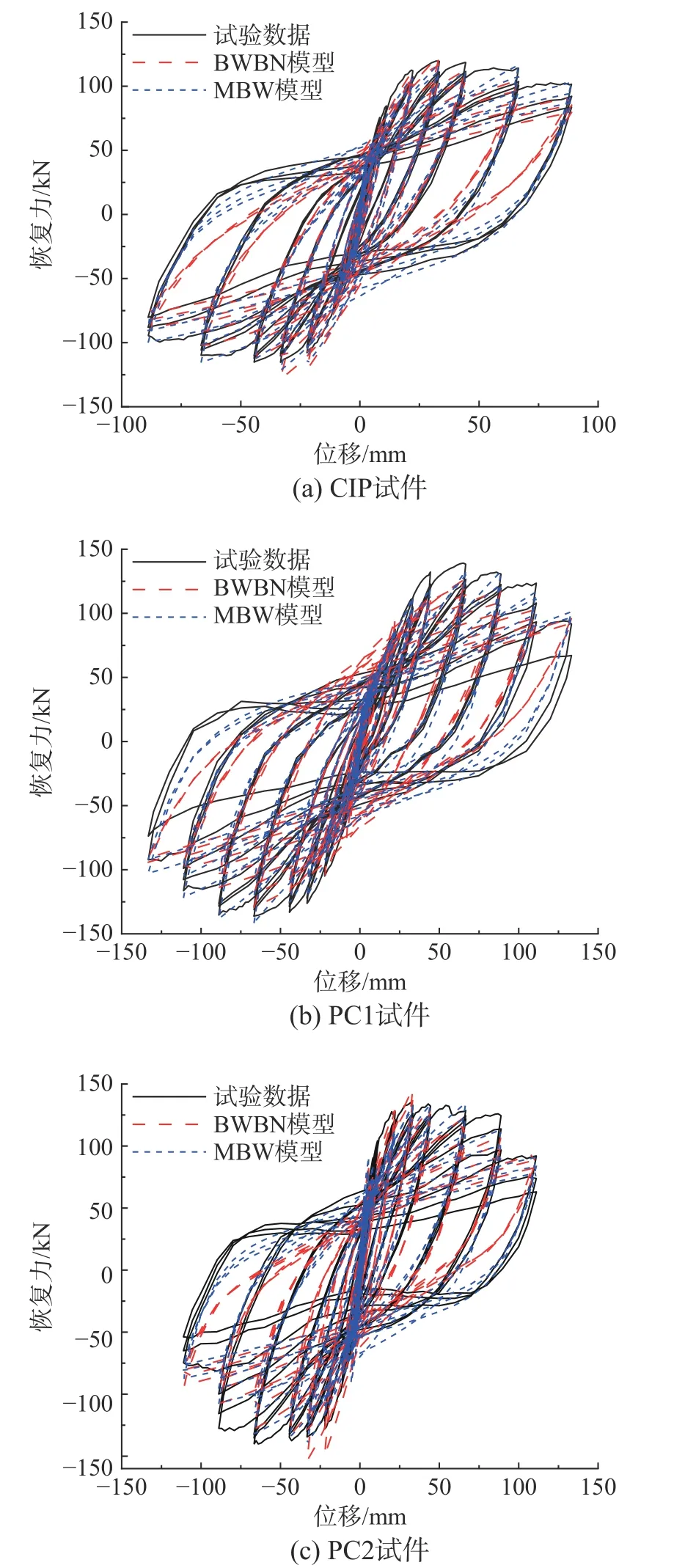
图16 试验结果与滞回模型之间滞回曲线对比Fig.16 Comparison of hysteretic curves between test results and hysteretic model
图17 将BWBN 模型和MBW 模型模拟得到的骨架曲线与试验数据进行对比分析。从图17 中可以看出,BWBN 模型和MBW 模型模拟的骨架曲线与试验数据在弹性阶段、屈服阶段和下降阶段具有相同的趋势。骨架曲线的正向峰值荷载和负向峰值荷载见表6,结果表明:MBW 模型模拟的骨架曲线与试验数据之间误差更小。
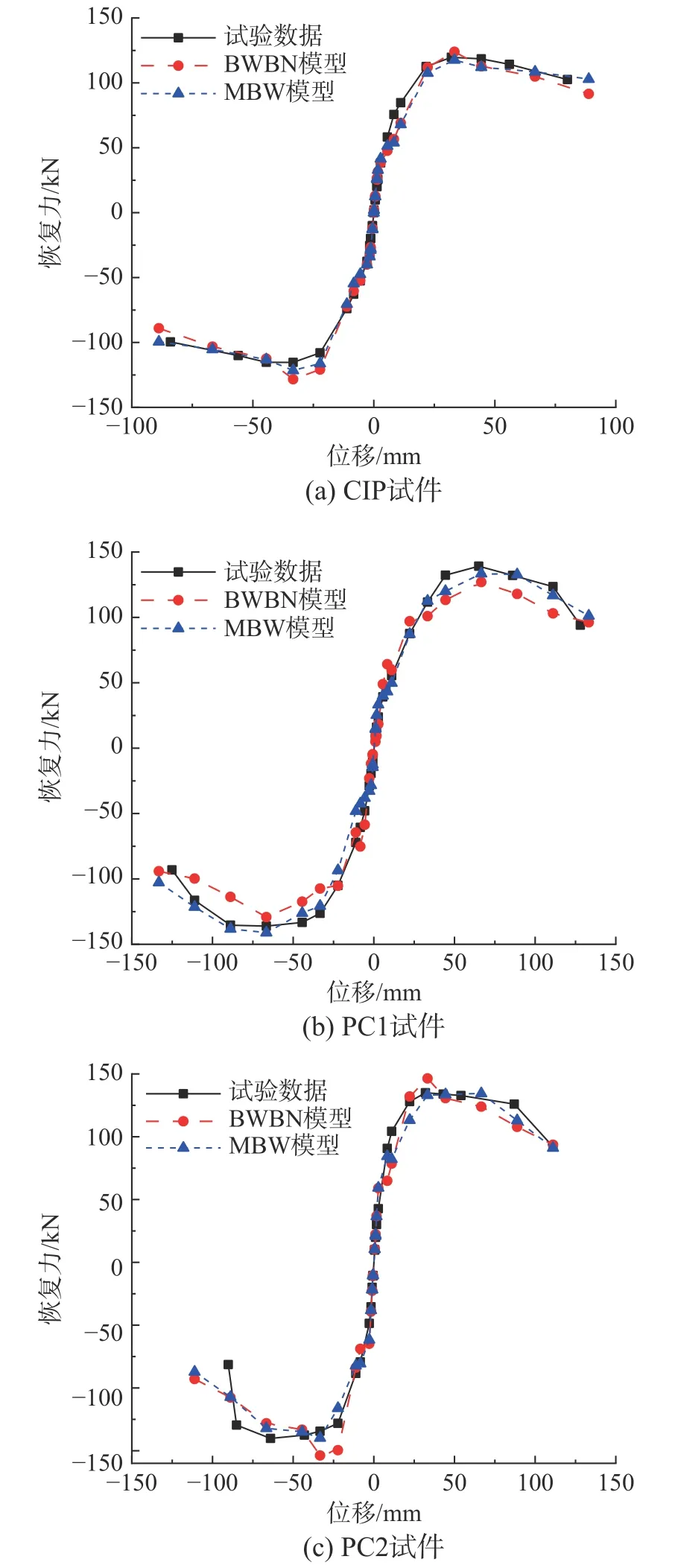
图17 试验结果与滞回模型之间骨架曲线对比Fig.17 Comparison of skeleton curves between test results and hysteretic model
图18 将BWBN 模型和MBW 模型模拟得到的累积滞回耗能与试验数据进行对比分析。从图18中可以看出,MBW 模型模拟得到的累积滞回耗能曲线与试验数据吻合更好。最终的累积滞回耗能见表6,结果表明:MBW 模型模拟得到的累积滞回耗能与试验数据之间误差更小。
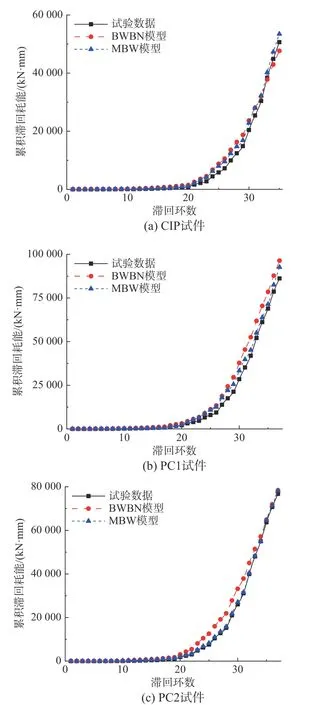
图18 试验结果与滞回模型之间累积滞回耗能对比Fig.18 Comparison of cumulative dissipated energy curves between test results and hysteretic model
综上所述,MBW 模型不但可以很好地模拟预制RC 桥墩的强度退化、刚度退化和捏缩效应等滞回性能,而且,与BWBN 模型相比,MBW 模型具有更高的计算精度。需要指出的是,由图15 可以看出,在第100 代时BWBN 模型的目标函数值轨迹仍有下降趋势,这说明,BWBN 模型具有继续进行参数识别、优化的空间,但是需要更多的进化代数、更大的计算代价才能达到MBW 模型第100 代结果的精度。
4 结论
由于Bouc-Wen-Baber-Noori (BWBN)模型中“捏缩效应”函数复杂且参数较多,其计算效率较低。鉴于此,本文基于近似狄拉克δ函数提出了新的改进Bouc-Wen (MBW)模型,并结合预制RC 桥墩的拟静力试验数据验证了MBW 模型的有效性,所得结论如下:
(1) 相比于BWBN 模型,MBW 模型的“捏缩效应”函数更加简单,能够以更少的参数实现捏缩效应。
(2) 本文建立的MBW 模型可以很好地模拟预制RC 桥墩的强度退化、刚度退化和捏缩效应等滞回性能。
(3) 与BWBN 模型相比,MBW 模型所得到的滞回曲线、骨架曲线、累积滞回耗能曲线与试验数据吻合更好,并具有更高的计算精度。

