基于哈里斯鹰算法的采摘机械臂机构优化设计

谢石璞

（长安大学，陕西 西安 710064）

0 引言

《“十四五”机器人产业发展规划》指出，要重点推进工业机器人、服务机器人、特种机器人重点产品的研制及应用，推动产品高端化、智能化发展[1]。采摘型机器人作为服务机器人的一种，承载着科技兴农、乡村振兴的重任。因此，采摘机器人的研发是十分关键的，其中，采摘机械臂又是采摘机器人的研究重点[2]。大多数的采摘机器人都会通过使用机械臂来拓宽其采摘范围，提升采摘性能。因而，机械臂设计的好坏将会直接影响机器人的采摘质量、采摘精度和采摘效率[3]。本文主要从结构尺寸设计的角度，对一种采摘机器人可重构模块化机械臂进行优化研究，而目前机械臂的结构尺寸优化一般是多目标的。

梁喜凤等[4]面向番茄采摘，以工作空间最大和结构最轻为目标，对机械手机构尺寸进行优化。赵江波等[5]针对救援机械臂，采用模糊层次分析法综合考量机械臂工作空间、末端运动速度以及负载，并以此建立优化目标函数，进行结构优化设计。马国庆[6]以高刚度、轻质量、运动灵活且平稳为设计目标，设计出一款符合人体工程学的服务型机器人。Gao等[7]以高系统刚度与灵巧度为目标对空间六自由度并联机器人进行优化。Zhang 等[8]归纳总结了近年来出现的机械臂性能指标，并将其分为两类，一类是运动性能指标，另一类是全域性能指标。针对采摘机械臂，一方面，要求其足够灵活可靠，即高的运动传递能力和运动传递精度；另一方面，要求其耗能较低，以适应田野环境。参考上述文献，本文使用能耗指标、可操作性指标、速度最小值、运动传递准确度来评价机械臂结构参数的好坏。

大多数情况下，难以对机械臂优化目标函数进行求导，即无法使用传统优化算法，因此智能算法应运而生。Yan 等[9]采用多目标粒子群优化算法求解空间机器人优化问题。王鑫等[10]采用多目标遗传优化算法，使机械臂各关节总功率以及各连杆长度达到最优。本文采用哈里斯鹰算法，该算法具有原理简单、参数少、稳定性高、收敛速度快等特点。本文的主要研究目标是针对采摘机器人的具体应用，从结构设计的角度，提出一套基于哈里斯鹰算法的机械臂设计优化方案。本文由机械臂运动学分析、指标分析与表述、约束条件的数学表述、机械臂优化模型、基于哈里斯鹰算法的模型求解与结果分析、结论六大部分组成。

1 机械臂运动学分析

1.1 物理模型的建立

机械臂构型示意图如图1 所示。图中采摘机械臂一共具有6 个转动副，分别位于图中的位置1 至位置6。机械臂6 个自由度中，前3 个自由度负责定位，后3 个自由度负责机械臂末端姿态。由于本文主要研究机械臂定位问题，所以将机械臂简化为如图2 所示形态。保留前3 个关节，并将后3 个关节等效为质点。其中，Oxyz为机械臂基础坐标系，d1为关节一的安装高度，θ1为关节一所转过的角度，L2为连杆二的长度，θ2为关节二所转过的角度，L3为连杆三的长度，θ3为关节三所转过的角度。

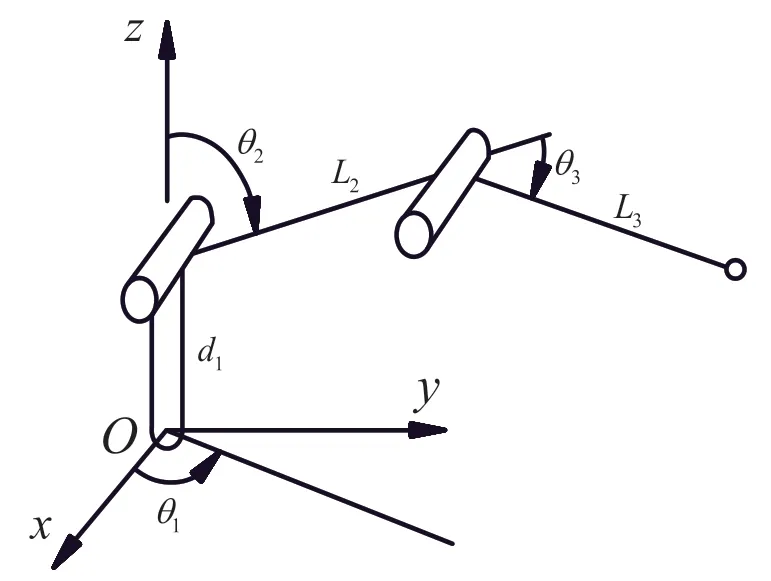
图2 简化运动模型

将简化后模型转化为标准D-H形式，标准D-H参数如表1所示。

表1 标准D-H参数表

1.2 雅可比矩阵的求解

由标准D-H 模型，可列出旋转、平移矩阵。旋转、平移矩阵相乘，可得关节间的齐次变换矩阵。一方面，由齐次变换矩阵依次两两相乘可得到机械臂末端相对于基础坐标系的姿态变换矩阵。另一方面，由齐次变换矩阵也可以得出相对雅可比矩阵。最终，由姿态变换矩阵与相对雅可比矩阵可求出雅可比矩阵，具体形式如式（1）所示。

2 指标分析与表述

2.1 功耗指标

采摘型机械臂的工作地点通常在种植园地，为获得稳定的电力供给，一般采用电池作为其能量来源。但是，电池本身也存在诸多问题，一方面，电池本身存储电力有限，限制了机械臂采摘工作的工作量。另一方面，将大量时间浪费在频繁地更换电池和电池充电上，也降低了整体的采摘效率。为解决上述问题，提高续航能力，从设计的角度来看，要寻找一组最优的设计参数使得机械臂功耗尽可能小。

机械臂的功耗，即机械臂采摘时的功率，其与机械臂运动时的角速度和工作力矩成正比。在获取到各部件具体的动力学参数之后，通过调节结构尺寸的办法，降低工作力矩并非难事。而对于角速度，其数值受采摘工况需求的限制，无法对其进行优化。

总之，提高采摘效率、续航能力的问题就转化为降低机械臂功耗的问题，最终转化为调节结构尺寸降低工作力矩的问题。为方便计算，本文将各机械臂关节的最大工作转矩和视作机械臂功耗。另外，为了厘清结构尺寸与工作力矩的关系，下一步需要对机械臂建立数学模型。

2.1.1 简化模型的建立

为方便进一步计算，对机械臂模型做出如下简化：

1）视各部件质量均匀，并将其简化为质点。

2）将关节质量分为两部分，减速器质量与其他质量，其他质量为常数，大小可通过称量法获得，减速器质量可通过查询减速器参数获得，减速器参数如表2所示。

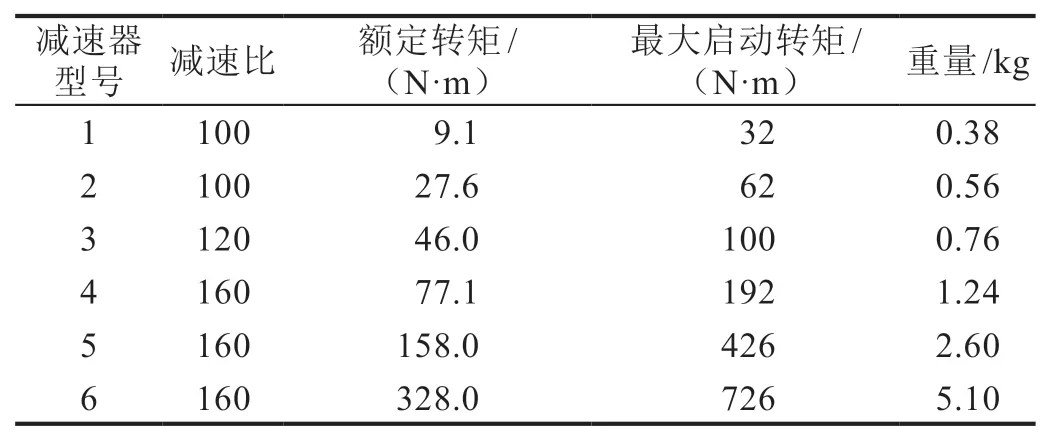
表2 减速器参数表

3）假设各连杆线密度相同。

4）将末端三自由度部件及负载简化为一质点，质量为ML。

简化后的机械臂物理模型，如图3所示。

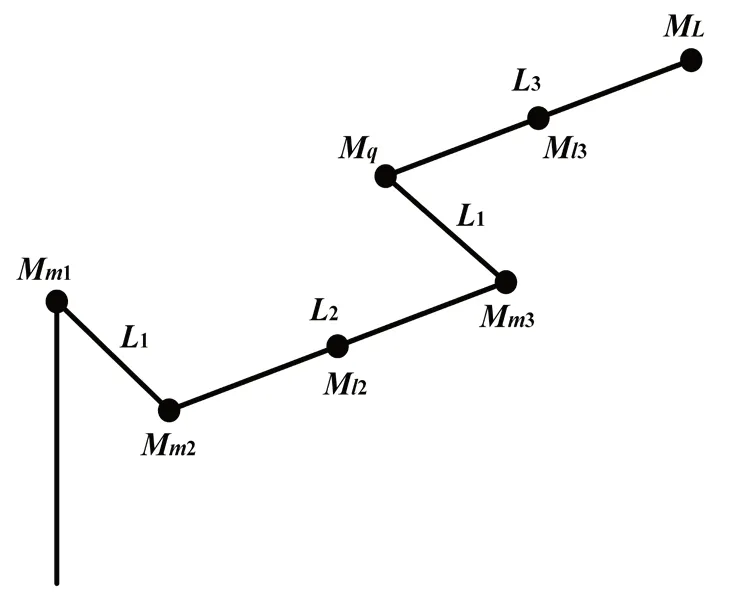
图3 简化模型的重量分布图

其中，Mm1表示关节一质量，Mm2表示关节二质量，Ml2表示连杆二质量，Mm3表示关节三质量，Mq表示空关节质量，Ml3表示连杆三质量，ML表示负载质量，L1表示连杆一长度，L2表示连杆二长度，L3表示连杆三长度。

2.1.2 数学关系的确定

由上述简化物理模型，计算各关节力矩：

其中，Mqi为第i个关节力矩，Mmi为第i个关节重力矩，Mgi为第i个关节惯性力矩，Jmi为第i个关节电机惯量，Joi为第i个关节的其他惯量，r是质量块的回转半径。式（2）中的r和L与结构尺寸L2、L3的取值密切相关。

结合简化模型和上述公式，可以明显得出：结构尺寸L2、L3和各部分的质量是影响工作力矩大小的主要因素，此时的工作力矩指的是各关节的力矩和。其中，结构尺寸L2、L3可以根据需求来确定。而对于质量因素，从实际出发，各部分质量存在变化和不变的部分，可视为质量不变的部分包括空关节、末端负载以及各活动关节中除减速器以外的部分；可视为质量变化的部分包括各活动关节中的减速器部分与各连杆。值得注意的是，关节中的减速器占关节总重的一半以上，且不同型号的减速器质量差异明显。

此时，各关节力矩和仍难以表示，主要是因为各关节中的减速器型号难以确定。究其原因，主要有两点：1）关节受到的负载力矩不同，设计时所选择的减速器型号也就不相同，负载力矩小的关节，可以选用小规格的减速器，其质量比较轻，反之，所选用的减速器就比较重。2）从机械臂末端到基座部分，前端的关节影响后端的关节，若前端关节质量比较大，则只能选用足够大的减速器，导致后端关节质量也会增加。

为克服上述两点问题，对于一组特定的L2、L3参数，本文将关节减速器选型工作融入求解力矩和的算法中，其算法流程如图4 所示。

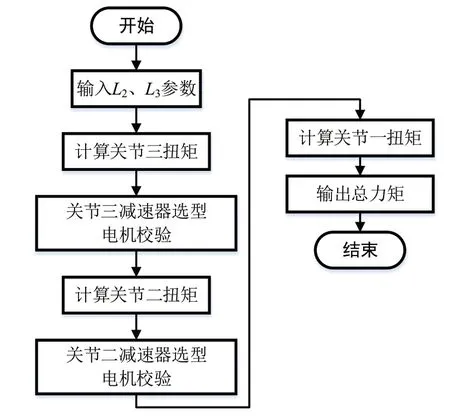
图4 计算机械臂总力矩的流程图

如图4 所示，算法倒序求解各机械臂关节力矩，求和得出最终结果。其过程为：根据L3、连杆三质量、负载质量以及关节三最大角加速度，即可求得关节三工作扭矩，进而根据减速器参数表完成对关节三减速器的选型工作，另外，对电机进行校验保证了电机的选型成功，至此，可计算出关节三质量。按此步骤，依次求解关节二、关节一工作扭矩，最终汇总得出减速器的总力矩。

设定初始域为L2∈[0.3，0.7]，L3∈[0.3，0.7]，利用上述计算机械臂总力矩的算法遍历初始域，可得如图5所示的结果。

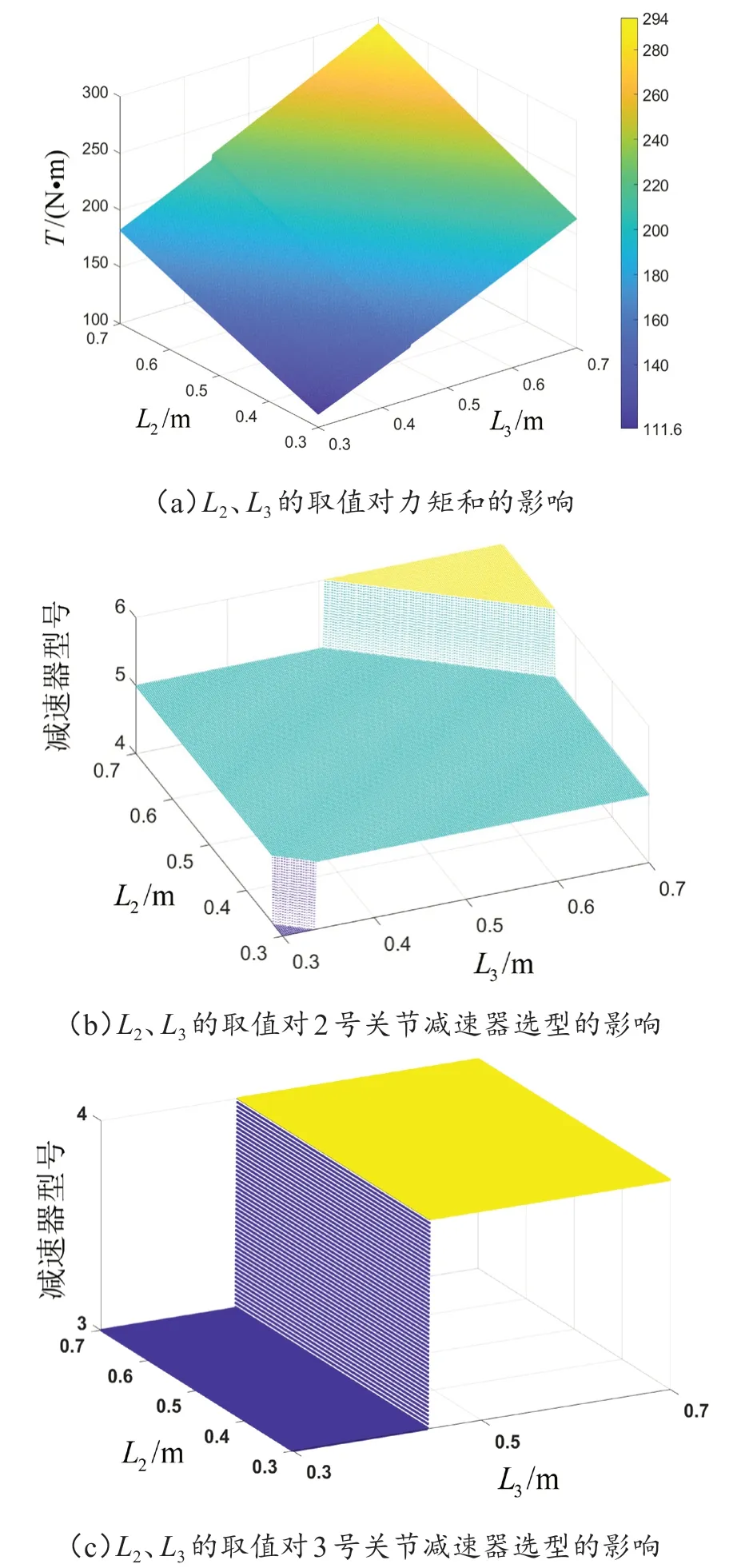
图5 L2、L3对力矩和与机械臂关节减速器的影响

由图5 可知，随着尺寸参数L2、L3的减小，力矩和也逐渐减小。当L2和L3均取最大值0.7 m 时，力矩和取最大值294.0 N·m。当L2和L3均取最小值0.3 m时，力矩和取最小值111.6 N·m。

2 号关节减速器的选型与L2、L3的取值有关，L2、L3越大，所选减速器的型号就会越大，其主要选取的减速器型号为5。3 号关节减速器的选型与L3有关，其主要选取的减速器型号为3与4。

2.2 可操作性指标

Mr代表机械臂末端的平均可操作性能。其值愈大，工作空间内平均运动传递能力就越强，直观表现为可操作性能越优异，在电机调速范围一定的前提下，机械臂末端运动速度的平均可调范围就越大。

其中，λ1、λ2、λm为JJT的特征值，m是特征值的数量，l为机械臂杆长之和。

2.3 速度最小值

vrmin代表工作空间中运动传递性能的最差值。若vrmin的数值过小，则即使面对末端速度变化很小的情况，关节处所需的速度变化范围也会很大，这显然是不可接受的，因此要求vrmin要足够大。

其中，min(λi)为JJT特征值中的最小值，min(σi)为J奇异值中的最小值。

2.4 运动传递准确度

kJ代表运动传递受制造装配等误差的影响程度。kJ越小，运动传递时受机器人制造、控制误差的影响就会越大，机器人运动准确性就越差，甚至最终导致机器人失控。总之，其值越大，运动传递受机器人本身误差的影响就越小，机器人的运动准确性越好。

其中，J+为雅可比矩阵的逆矩阵。σmin、σmax分别为J奇异值中的最小值与最大值。

运动学性能可分为运动传递能力和运动传递精度，本文中涉及有关运动传递能力的性能指标为可操作性指标与速度最小值，有关运动传递精度的性能指标为运动传递准确度。

2.5 全域性能综合评价指标

当涉及机械臂杆长参数优化设计时，通常考虑其在全域工作空间下的性能指标分布情况，而不是关注其在某工作点性能指标的具体数值。由描述统计学理论可知，若要综合评价指标的全域性能，则应同时关注其中心趋势、分散程度、分布形状。另外，在综合不同指标时，也应去除性能指标之间单位不同所带来的影响。

2.5.1 平均值指标

ξavg相当于评价指标在工作空间中的平均值，代表评价指标的集中趋势。其值愈大，代表评价指标整体水平愈高。

其中，ξ代表评价指标的数值，W代表机械臂的工作空间。

2.5.2 波动性指标

ξvol代表评价指标在工作空间中的波动性，其值愈高，指标在空间中离散程度越高，整体性能越差。

其中，ξsd代表评价指标在工作空间中的标准差数值。

2.5.3 偏度指标

ξskew代表评价指标在工作空间中的偏度，主要描述指标在空间中分布的不对称性，其绝对值越小，其相对于空间中心越对称。偏度的正负仅仅代表分布偏离中心的方向。

2.5.4 峰度指标

ξkurt代表评价指标在工作空间中的峰度，是衡量评价指标相较于正态分布是尖锐还是扁平的工具。当峰度为0 时，其尖锐程度同正态分布；当峰度为正值时，其分布相较于正态分布更加尖锐；当峰度为负值时，其分布外观更为平坦。

3 约束条件的数学表述

3.1 工作空间约束

图6 为根据实际采摘场景提取出的工作空间示意图，其中，连杆结构为机械臂，长方体为工作区域，其长度为d，宽度为b，高度为h。机械臂关节一与工作空间的最短距离为Lx，其中心位于工作空间上下等分面上。空间距离中心最远点为A、B、C、D。因此，若要使机械臂达到最远点，则关节二与关节三的长度之和要大于最远距离。即式（10）所示：

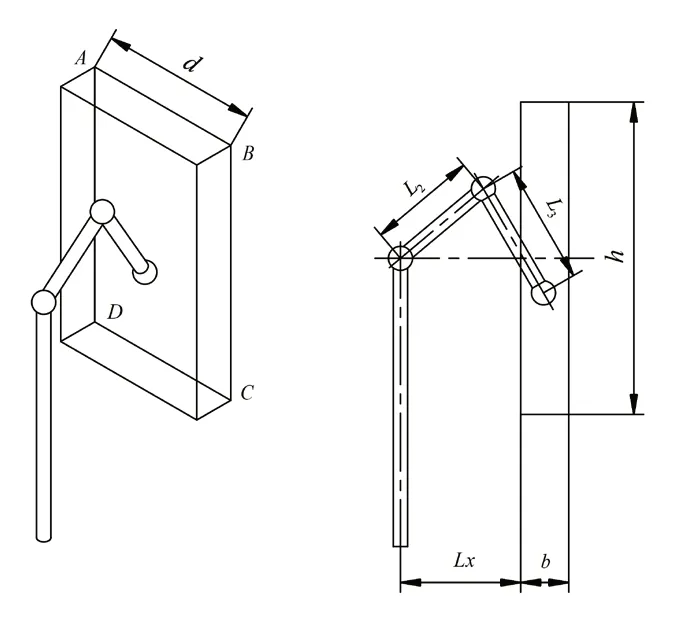
图6 工作空间约束示意图

为了保证机械臂能够有较大的工作空间，连杆二与连杆三的杆长相差不能过大，且工作空间内侧边界应该至少能够在行走底盘上方空间内，如图7 所示。其数学表述形式为：

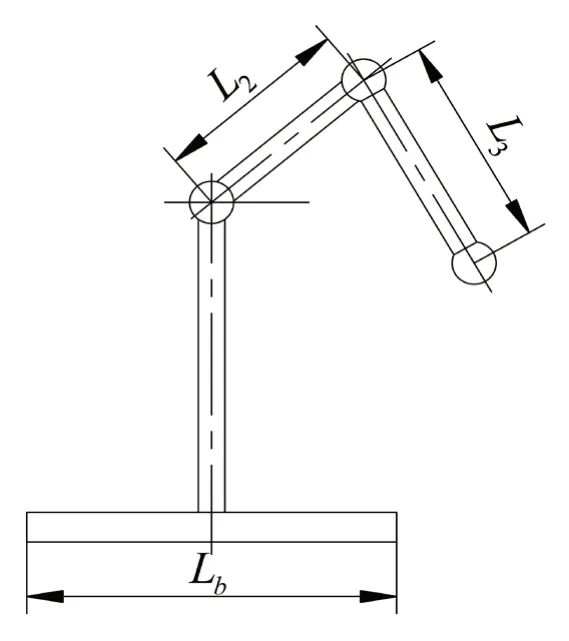
图7 带有行走底盘的机械臂示意图

其中，Lb为行走底盘宽度。

3.2 工作条件约束

采摘时，在连杆二与水平方向夹角θ为90°左右时，随着连杆二的左右摆动，连杆二末端质量块会使连杆二受到近似对称循环变应力作用，导致杆件结构产生疲劳形变，丧失定位精度，造成机械臂提前失效（机械臂的主要失效形式为定位精度丧失）。为避免连杆二处于此受力状态，规定夹角θ应小于89°。取两种极限状态，对其进行约束。

状态一，当末端位于长方体工作空间靠近机械臂一侧上沿终点时，夹角θ有可能取得最大值，如图8所示。由三角函数公式，经化简可得：

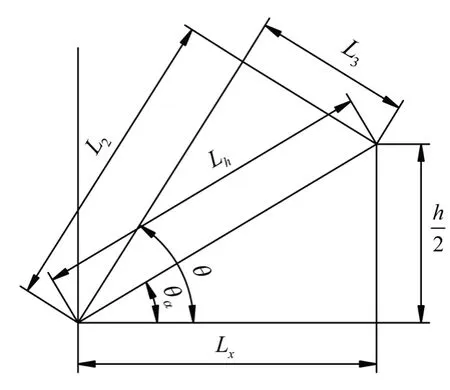
图8 状态一构型示意图

状态二，当末端位于长方体工作空间中距离关节一中心最近点时，夹角θ有可能取得最大值θβ，如图9所示。由余弦定理可得：

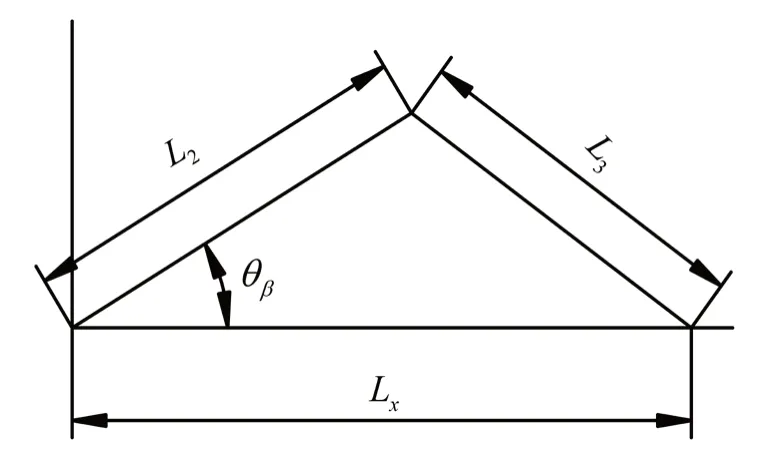
图9 状态二构型示意图

4 机械臂优化模型

本章综合第二章所提到的关键性能指标与第三章所归纳的约束条件，建立数学优化模型。

综合考量上文所提性能指标，提出目标函数（也称适应度函数）公式：

其中，β1、β2、β3、β4为各性能指标所属的权值，T为关节力矩和，Mr为可操作性指标，vrmin为速度最小值指标，kJ为运动传递准确度，下标为integr的参数为全域性能评价指标。式（14）去除了各指标单位与绝对大小的影响。

要使得目标函数全局达到最优，则功耗指标应尽可能小，可操作性指标应尽可能大，速度最小值应尽可能大，运动传递准确度应尽可能高。一般优化算法将目标函数的全域最小值视作最优，因而β1应为正值，β2、β3、β4应为负值。同时作为采摘型机器人，以低功耗与高运动传递准确度为重，同时考虑可操作性与速度最小值因素。因此，令β1=1，β2=-0.1，β3=-0.1，β4=-1。

将上述权值代入目标函数式（14），可得：

下面将使用ξ指代性能指标，即Mr、vrmin、kJ，则全域性能评价指标(ξ)integr的计算公式可以表述为：

其中，α1、α2、α3、α4为各全域分布特征的所属权值，ξavg为分布平均值特征，ξvol为分布波动性特征，ξskew为分布偏度特征，ξkurt为分布峰度特征。

据某文献所述，可取α1=1，α2=-ξavg，α3=-0.1ξavg，α4=-0.1ξavg。将上述值代入式（16）可得：

即采摘机器人尺寸优化数学模型可表述为：

其中，Lmin=0.3 m，Lmax=0.7 m，Dmax=1.0 m，Lb=0.62 m。

由约束条件可得，可行域可进一步缩小为如图10所示的黄色区域，横坐标为L2，纵坐标为L3。

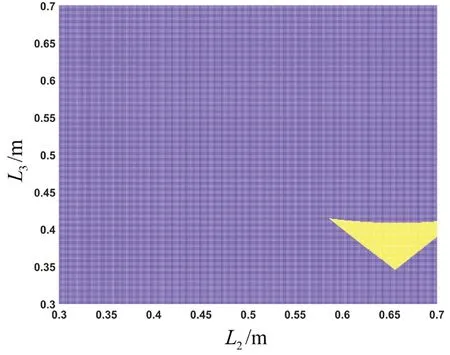
图10 初始域与可行域范围

5 基于哈里斯鹰算法的模型求解与结果分析

5.1 哈里斯鹰算法简介

哈里斯鹰作为自然界中最聪明的鸟类之一，其围捕猎物时，总是成群结队，相互合作。它们会从发现猎物开始，轮流袭扰猎物，消耗其精力；直至猎物疲惫，鹰群转换为围捕模式，并施展突袭策略，此时猎物同样会释放假动作来迷惑鹰群，但随着猎物力竭，鹰群终会获胜。2019 年，Heidari 等[11]受上述狩猎行为的启发，提出了哈里斯鹰算法，其同蚁群算法、人工蜂群算法一样属于群智能优化算法。值得注意的是，它们与共轭梯度法或最速下降法等传统方法并不相同，并不依赖于问题本身的梯度信息或其他数学特性，降低了对问题的要求，拓展了算法的适用性。尤其是在优化问题无法用简洁的公式表示的情况下，群智能优化算法具备明显优势。

5.2 算法原理

哈里斯鹰算法模仿了鹰群的狩猎行为，鹰群的位置代表着一组候选解，而猎物的位置代表当前最优解，鹰群追捕猎物本质上就是算法在不断寻求最优解。算法运行过程可分成三个阶段：探索阶段、探索到开发过渡阶段以及开发阶段。

在探索阶段中，鹰群会随机分布在其栖息地内等待并寻找猎物，此时鹰群位置的更新会依赖于两种策略。一种是鹰群会在栖息地内随机选取落脚点，另一种是其落脚点的选取会依赖于猎物与其他鹰的位置。而这两种策略的选择完全随机。

在探索到开发过渡阶段中，算法指出猎物在鹰群的追捕下，其精力总体上会不断地被消耗。猎物精力比较旺盛，代表着此时鹰群正在栖息地内的不同区域不断搜寻猎物，此时鹰群处于探索阶段。当猎物的精力低于某一数值时，暗示着鹰群正在某特定区域不断围捕猎物，此时鹰群处于开发阶段。

在开发阶段中，鹰群不断围捕猎物，并时常发动俯冲突袭，而猎物也会不断释放假动作来迷惑捕食者。视猎物成功突破包围的概率与失败的概率相同。鹰群会依照猎物的具体情况不断切换进攻策略。当猎物未能突破包围且精力比较充足时，鹰群采用软包围策略，不断消耗猎物的精力；当猎物未能突破包围且没有精力时，鹰群采用硬包围策略，不断靠近猎物；当猎物突破包围且精力比较充足时，鹰群采用渐进俯冲的软包围策略，鹰不断发动随机俯冲，猎物也会不断施展更多的假动作，算法采用列维飞行函数来描述上述运动随机性；当猎物突破包围且没有精力时，鹰群采用渐进俯冲的硬包围策略，不断向猎物聚集，鹰与猎物的平均距离不断缩小。

综上所述，HHO算法流程如图11所示。

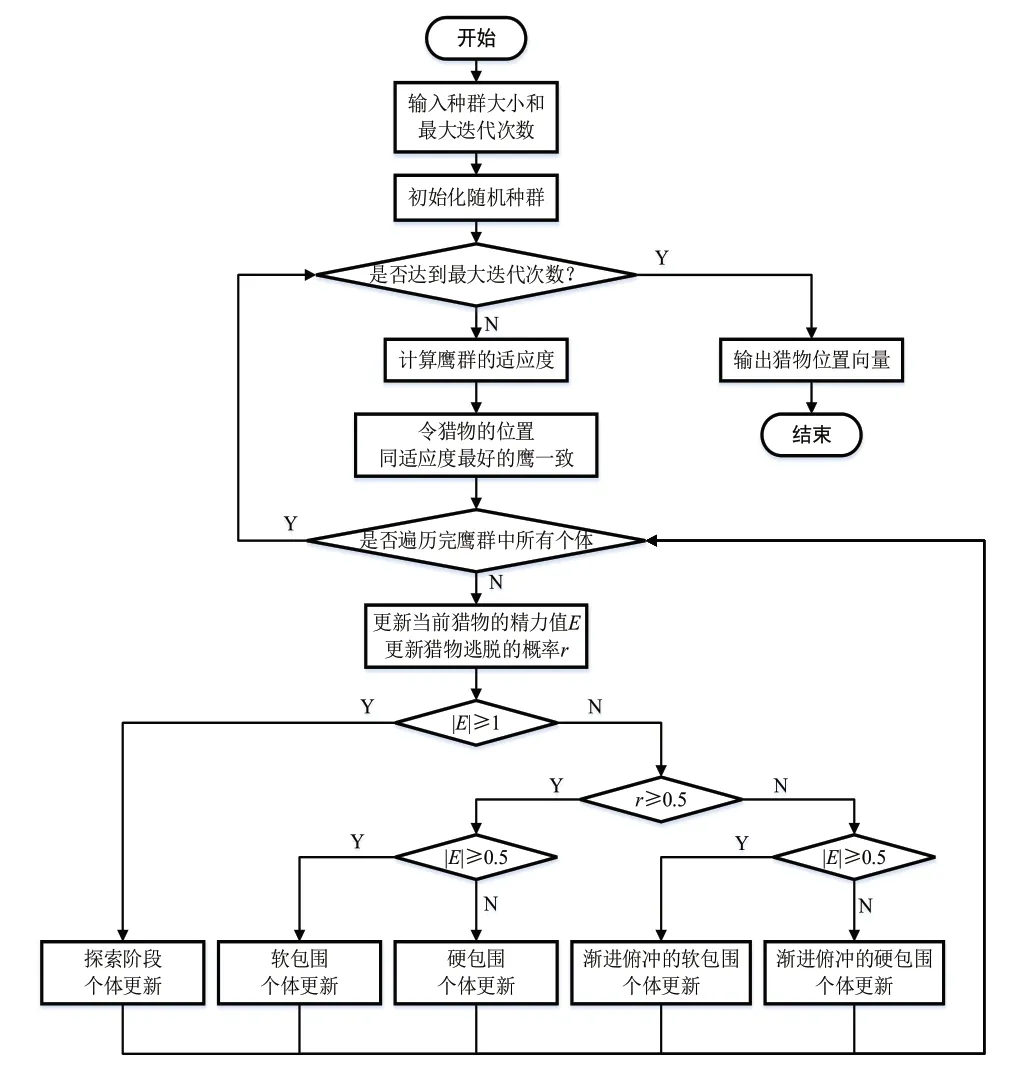
图11 HHO 算法流程图

5.3 机械臂优化问题求解

5.3.1 求解优化案例

通过对哈里斯鹰群狩猎活动的深度理解并对过程进行抽象建模，建立其群体狩猎行为与HHO 算法中各要素之间的对应关系，如表3所示。

对于本文所讨论的采摘机械臂杆长优化问题，其相关求解参数具体为：适应度函数为式（18），栖息地范围为式（19）所限定的区域，鹰的种群大小设定为5，其狩猎时长，即最大迭代次数设定为20。

将上述参数代入HHO 算法中进行求解，获得迭代次数达到最大值时的优化变量取值以及相应的目标函数值，即目标函数最小值。

5.3.2 优化结果分析

优化求解结果如图12 所示，由计算结果图像可知，HHO 算法仅迭代一次，就获取了最优的结果，当L2=0.656 m，L3=0.346 m 时，目标函数取得最小值，为-0.952。

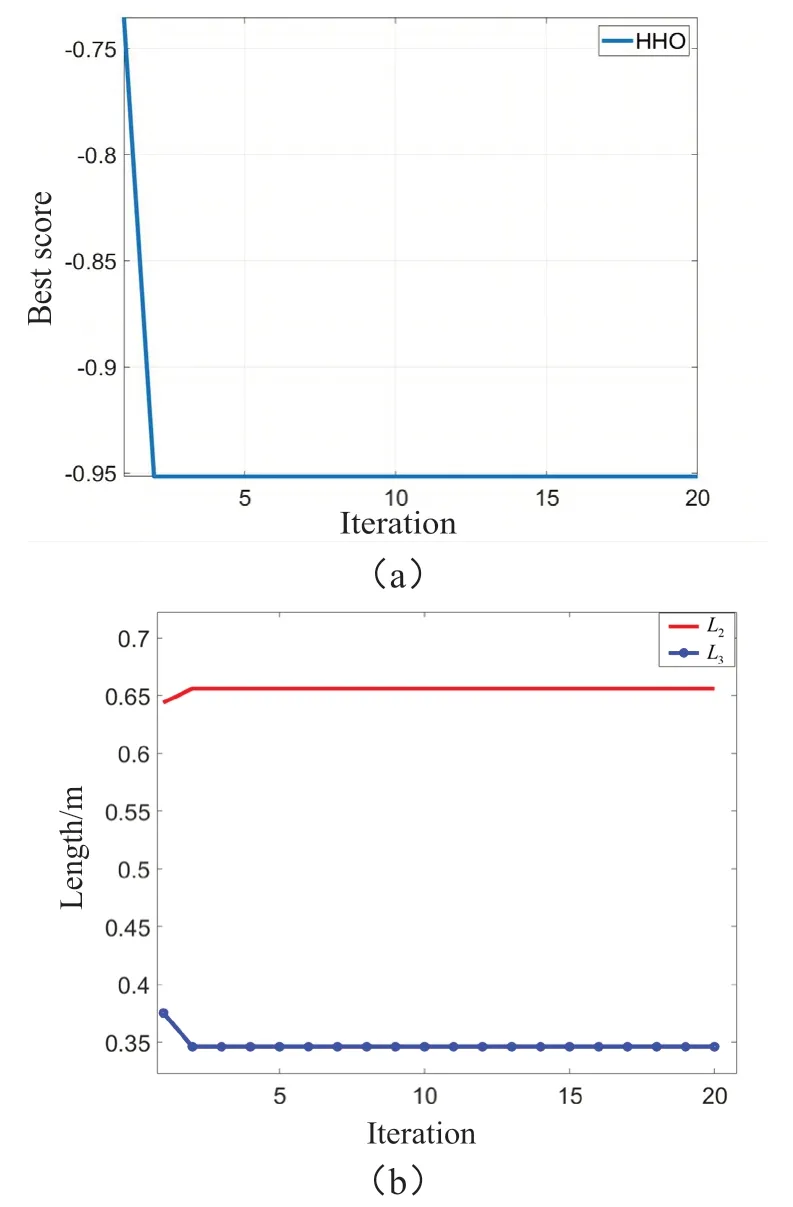
图12 优化求解结果

借助性能指标求解公式，求得此时关节力矩和为185.7 N·m，为初始域中的最大值（294.0 N·m）的63%，又因其在可行域中的值域为[185.2，210.6]，可视作当前处于关节功耗最小状态。同理，求出(Mr)integr、(vrmin)integr、(kJ)integr的当前值和其在可行域内的值域，结果如表4所示。

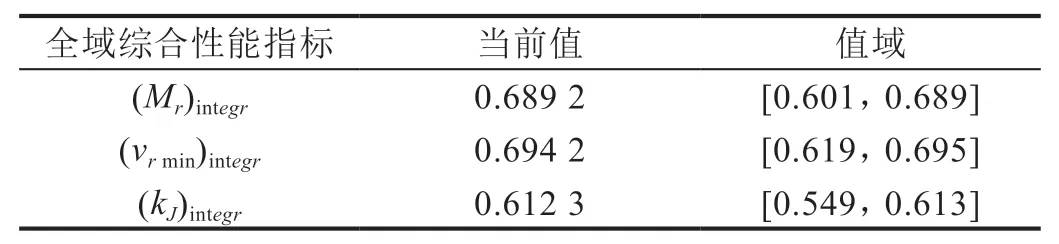
表4 全域综合性能指标的当前值与值域

由表4 可以看出，各项全域综合性能指标的当前值均已达到最优结果。因此，可将L2=0.656 m，L3=0.346 m 视作可行域内的最优结构参数。

6 结论

1）从采摘机械臂实际设计需求出发，以低功耗与高运动传递能力为目标，采用功耗指标、可操作性、速度最小值、运动传递准确度等多种尺度对机械臂进行综合评价，并考虑工作空间与工作条件等因素，搭建了采摘机械臂机构优化模型。通过对上述模型进行求解寻优，获取一组最优的关键设计参数，为机械臂后续的设计工作提供指导。

2）以采摘机械臂中负责定位的三个关节所受最大力矩之和为功耗指标。在求解关节最大力矩时，抓大放小，将减速器质量作为关键影响因素，将计算力矩与减速器选型过程相融合，解决了无法确定关节质量的问题，进而确定了力矩。并由于关节之间的影响具有方向性，即靠近末端的关节影响靠近基座的关节，求解过程采用倒序求解的方法。上述求解过程提供了在设计阶段估算关节力矩的一种方便可行的思路。

3）本文采用HHO 算法提供了一种针对目标函数无法求导的优化问题的求解思路，其迭代过程仅进行了一次，就获得了可行域中的最优解，展现了其高效的求解过程。