混合果蝇优化算法PID 参数整定方法的研究*

陈 亮 ，李助军 ，邹伟全 ，李西兵

（1.福建农林大学机电工程学院，福建 福州 350000；2.广州铁路职业技术学院机电工程学院，广东 广州 510000）

0 引言

在工业4.0 时代背景下，精密控制技术的应用将变得更加广泛。例如，外科手术中的医用机器人可用更精准、侵入性更小的方式进行手术[1-2]。精密控制涉及多种技术和方法，包括传感器技术、控制算法、运动控制技术、机器视觉等。其中，控制算法是精密控制的核心部分，常用的控制算法包括比例积分微分（PID）控制、模糊控制、神经网络控制等。PID 控制器作为最常见的控制器，算法实现简单，应用范围广。自从PID 控制器产生以来，如何快速、方便地整定PID 参数一直是学术界、产业界的研究重点。传统的PID 控制器往往容易出现超调、响应时间长、易发生震荡等缺点。由于计算机的处理性能不断提升，越来越多的智能优化算法运用在PID 参数优化中。台湾学者Pan 在2011 年提出了一种模仿果蝇觅食行为的群智能算法——果蝇优化算法（FOA）[3]。该算法具有简单、计算量小、适用度高、容易和其他算法结合得到更优的算法等优点，被多个学者进行优化并且运用在不同领域[4-5]。李明辉等提出一种自适应果蝇优化算法的PID 参数优化法，以控制偏差绝对值和输入平方项的时间积分作为适应度函数，经过迭代寻优得到最优的PID 参数值[6]。Liu 等将混沌搜索与FOA 算法结合来整定PID 参数，有效降低了适应度波动[7]。韦修喜等将混沌映射、判别因子与变步长机制引入果蝇优化算法得到改进后的自适应混沌果蝇优化算法（fruit fly optimization algorithm with chaos and discriminant factors, CDFOA），利用CDFOA 优化BP神经网络的初始权值与阈值，解决了BP 神经网络存在预测精度不佳、预测结果不稳定的问题[8]。李猛等采用变换函数确定自适应步长，提出一种动态步长果蝇优化算法（dynamic step fruit fly optimization algorithm, DSFOA），提升了算法的收敛精度和搜寻效率[9]。

对基本果蝇优化算法（FOA）的PID 参数整定在收敛过程中比较缓慢且容易过早陷入局部最优的缺陷的问题进行了研究，提出了混合果蝇优化算法（HFOA）PID 参数整定方案。通过粒子群搜索机制和适应度函数选择出多个优秀粒子，在优秀粒子周围生成果蝇种群，再用FOA 对种群进行迭代寻优，寻找出最优参数。仿真结果表明，该算法收敛速度快并且能够准确地寻找到最优参数，很大程度上避免了陷入局部最优的情况，有效提高了PID控制器的控制精度。

1 PID控制器基本原理

PID的控制规律为：

式中，KP为比例系数；KI=KP/TI，为积分增益；微分增益为KD=KPTD。

比例系数KP用于反映系统的偏差信号e(t)，当系统输出结果出现偏差，控制器立即成比例地产生控制作用，减少误差，KP越大系统达到目标越迅速，但过大的比例系数容易使系统产生超调。积分增益KI主要用于消除系统静态误差，提高系统的无差度，KI越大系统越容易达到目标位置，但过大的积分增益也容易导致积分过饱和从而出现超调。微分增益为KD反映了偏差信号的变化率，并在偏差信号过大时引入一个有效的矫正信号，从而减少系统的调节时间，KD越大越能有效减少系统超调，但同时也会延长系统的调节时间。所以，要选择合适的控制参数才能够使系统的输出满足稳定、准确、快速三个指标。

2 算法介绍及改进

2.1 基本果蝇优化算法

果蝇优化算法（FOA）是一种模仿果蝇觅食过程的区域内全局优化的新方法。果蝇本身在感官知觉上优于其他物种，尤其在嗅觉与视觉上。果蝇的嗅觉器官能很好地搜集飘浮在空气中的各种气味，甚至能嗅到40 km 以外的食物源，在果蝇个体依靠嗅觉发现食物源位置方向后，立刻朝该方向飞去，到达食物位置附近后再依靠敏锐的视觉发现食物和同伴聚集的位置，并且往该方向飞去[10]。果蝇觅食行为示意图如图1所示。

图1 果蝇觅食行为示意图

果蝇优化算法寻优过程如下：

1）初始化果蝇种群数量、迭代次数和每个果蝇个体的初始位置（x，y）。

2）每个果蝇（x，y）随机向不同方向和不同距离前进到（xi，yi）。

其中，a为随机生成的值。

3）由于不能确定食物的具体位置，计算果蝇到原点的距离Di，然后得到味道浓度判定值Si，代入适应度函数F(Si)中得到果蝇个体的味道浓度Smelli。

4）在果蝇种群中找到最优的味道浓度和个体。

5）记录最优味道浓度Smellbest=bestSmell并将坐标（xb，yb）保留下来。

重复步骤2 至步骤5 进行迭代寻优，记录当前浓度并判断是否优于前一次的最佳浓度，如果是便替代最佳浓度进行下一次迭代。

2.2 混合果蝇优化算法

由于果蝇算法无论在寻优初期还是后期均根据式（2）进行位置分配，固定搜索位置就导致在算法搜索前期搜索效率低而在搜索后期又容易错过最优解。通常情况下，在寻优过程初期，需要更好的全局搜索能力[11]。混合果蝇优化算法流程如图2 所示，由于算法的初始解是随机生成的，为了减少迭代过程中的计算次数，可以根据优化目标函数值对初始解进行初步筛选[12]。在果蝇迭代寻优前，利用粒子群算法优秀的全局搜索能力在范围内标记出多个优质粒子，优质粒子在果蝇觅食过程中代表的就是食物更容易出现的点，再在优质粒子附近生成若干果蝇形成的种群，种群内每个果蝇随机向不同方向和不同距离前进并进行迭代。根据适应度函数对所有果蝇筛选出最优的果蝇个体以及对应的种群，记录下所在种群经过迭代后的最优果蝇个体位置。

图2 混合果蝇优化算法流程图

3 基于HFOA的PID参数优化步骤

3.1 控制性能指标的选取

为了防止初始误差较大影响获取理想的动态特性，采用误差绝对值的时间积分性能指标作为最小目标函数[13]。所以本文在粒子群优秀个体的筛选和果蝇迭代过程中都采用绝对误差积分作为主要的性能指标：

其中，e(t)=rin(t)-yout(t)，rin(t)为输入量，yout(t)为经过PID控制系统后的输出。

为了避免系统出现超调，应当引入w2|e(t)|作为惩罚机制。当系统出现超调时，即当e(t)＞0 时，性能指标为：

其中，w2＞＞w1，本文取w2=100，w1=1。

优质粒子的适应度范围为：

其中，ITAEh(i)为达到优秀粒子条件的最大适应度，ITAEmin(i)为最佳适应度，n为常数。

3.2 HFOA在PID参数优化中的应用

基于混合果蝇优化算法的PID 参数整定原理如图3所示。

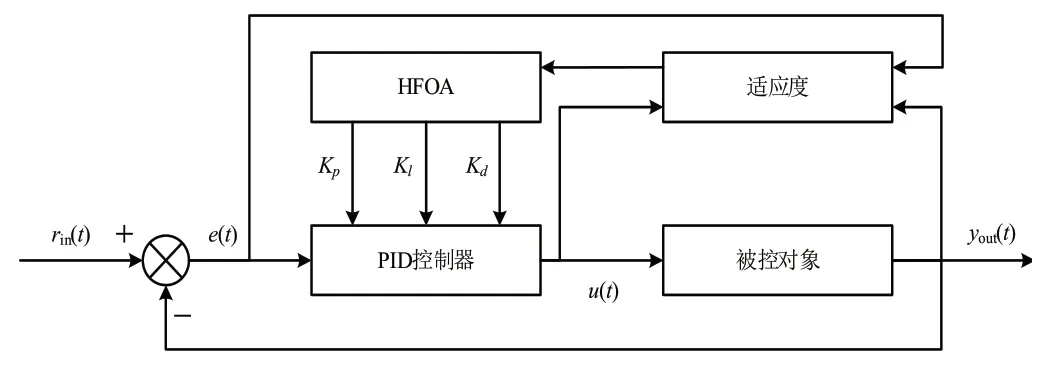
图3 HFOA 的PID参数整定原理

HFOA 算法用于PID参数整定的步骤如下：

1）粒子群初始化，如粒子群规模、粒子群生成范围、粒子所在位置等，由于PID 控制器有KP、KI、KD三个参数，故选定粒子位置为：

2）通过式（7）计算各粒子适应度ITAE(i)，用式（8）筛选出优质粒子并进行保存。优质粒子所在位置为：

3）在优质粒子周围区域生成果蝇种群，设置果蝇种群大小sizepop 最大迭代次数maxgen。初始化每个果蝇个体位置X。可以根据实际应用场景限定果蝇个体位置出现范围：

其中，X(1)、X(2)、X(3)对应优质粒子X的三个坐标kp、ki、kd，a、b、c为选定的常数。

4）根据式（12）随机分配果蝇寻找食物的方向和距离，为了保证果蝇迭代后种群收敛，引入收敛系数wn=w*λi，其中λ=0.95，w为常数，i为当前种群个体迭代次数。

5）通过式（7）计算每个种群适应度，从果蝇种群中寻找最优的浓度和个体，果蝇自适应搜索位置更新。

6）进行果蝇迭代寻优，步骤4、步骤5 循环进行，判断此次浓度是否优于上一次最佳浓度、是否小于最大迭代次数，如果是，便更新最佳浓度。输出最优个体气味浓度Smellbest和PID控制的最优参数Xbest。

4 仿真实验与结果分析

4.1 控制对象以及仿真条件确定

在工业控制中，大多数控制对象可以看作二阶延迟系统。将两个典型二阶带延迟的传递函数作为控制对象进行研究，分别用FOA、PSO、HFOA 对PID 控制器的参数进行整定。选定的两个控制对象传递函数为：

对系统进行仿真，仿真环境为MATLAB2021a。输入信号采用单位阶跃信号，采样周期为0.001 s。

在FOA 和PSO 算法中，设置粒子群规模为300，初始控制参数KP、KI、KD为5、0.1、0.1。KP的随机范围为[0，100]，KI的随机范围为[0，20]，KD的随机范围为[0，20]。设定果蝇种群大小为30，迭代次数为100。

在HFOA 算法中，设置粒子群规模为300，KP的随机范围为[0，100]，KI的随机范围为[0，20]，KD的随机范围为[0，20]。设定果蝇种群大小为30，迭代次数为100。迭代过程中果蝇个体出现的范围KP、KI、KD根据式（2）、式（10）确定，其中，收敛系数wn=w*λi，w1=1、w2=0.02、w3=0.1、λ=0.95，i为当前种群个体迭代次数，a、b、c分别取10、0.2、0.05。

4.2 仿真结果分析

选取上升时间、调节时间、超调量和ITAE作为控制性能衡量指标；使用三种算法对PID 参数分别进行优化，计算100 次取平均值，所得出的计算结果如表1所示。

表1 3种算法的 PID 优化参数对比

其中，上升时间是输出信号从稳态值10%上升到90%所需的时间；超调量是响应过程中输出量超出稳态值的最大偏差值所占稳态值的百分比；调节时间是输出衰减到稳态值的偏差小于2%或5%所经历的时间，在本文中选定偏差小于2%所经历的时间。由此可见，上升时间越短，系统响应越快；超调量越小，系统越稳定；调节时间越短，系统达到稳态值越迅速，系统越准确。

由表1 计算结果中的ITAE值可知：基于HFOA 的PID 控制方法的收敛精度要高于其他两种方法。此外，由表1 给出的上升时间和调节时间也可以得出：基于HFOA 的PID 控制方法在控制过程中，被控系统达到稳定的时间相对较短。

被控系统G1(S)、G2(S)分别采用三种算法控制的系统单位阶跃响应输出曲线和运算迭代曲线如图4、图5、图6和图7所示。

图4 系统1的阶跃响应

图5 系统1的适应度函数曲线

图6 系统2的阶跃响应

图7 系统2 的适应度函数曲线

由图中的系统运算结果可以得出：HFOA 相对于其他两种算法迭代次数更少，误差积分波动更小，表明了HFOA 算法收敛更加迅速并且更加稳定，体现了HFOA 在PID参数优化中的有效性。

5 结论

针对基于基本果蝇优化算法（FOA）的PID 参数整定由于算法局限性而出现参数收敛速度慢且容易过早陷入局部最优的问题，对基本果蝇算法进行算法协同学习优化研究，提出了一种将粒子群算法和果蝇算法融合的PID 参数的整定方法，该算法在迭代前期使用具有更高的全局搜索效率的PSO 算法提高收敛速度；在迭代后期使用具有较强局部寻优能力的FOA 算法提高收敛精度，实现对全局搜索和局部搜索过程的优化。使用MATLAB2021a 进行仿真，仿真结果表明，相比于PSO 算法和FOA 算法，基于HFOA的PID 控制器参数整定的上升时间、调节时间和超调量等指标更优，能够使系统有更好的响应性能。与FOA 算法和PSO 算法相互比较可知，HFOA 算法迭代次数少并且迭代稳定性好。同时，使用HFOA 算法对PID 参数进行整定不需要初始的KP、KI、KD控制参数，相对于基本FOA 算法具有更高的适用性。因此，基于HFOA 算法的PID 参数优化研究对精密控制领域具有一定的参考价值。