基于响应灵敏度方法的螺栓连接结构参数识别及实验*

廖华松， 陈海， 汪利， 杨达豪， 吕中荣

中山大学航空航天学院，广东 深圳 518107

在航空航天等领域中，常用的结构连接装配方式有3 种：焊接、铆接及螺栓连接（Shen et al.，1999）。螺栓连接因具有良好的灵活性和互换性，在精密构件和工程制造中应用较广。然而，螺栓连接导致接触表面存在机械摩擦，带来显著的阻尼效应、刚度折减以及能量耗散，呈现出复杂的非线性动力响应（Argatov et al.，2011）。该非线性特性可以由微观滑移-宏观滑移描述。发生滑移时，螺栓孔周围的区域位移仍然被限制，而该区域的边缘开始滑动，这种现象称为微滑移。只要滑移仍在微滑移阶段，螺栓连接部位的刚度都会呈现轻微下降的趋势，而阻尼会呈现出显著增加的趋势（Shetty et al.，2023）。一旦外激励达到足以发生相对滑移的程度，结构之间发生宏观滑移，结构刚度便会显著降低。

为描述螺栓连接部位的粘滞-滑移特性，相关学者提出了Ⅰwan 模型。Ⅰwan 模型由大量的Jenkins单元（往往含有10-100个状态变量）并联组合而成。每个Jenkins单元由单个弹簧和库仑滑块并列而成，具有典型的粘滞-滑移特性，是显著的非光滑单元（Segalman， 2001）。为求解Ⅰwan模型所表征的滞回响应曲线，需要求解几十个Jenkins 单元滑块的状态变量，存在计算量大、非线性程度高等不足。Bouc-Wen 模型的非线性主要来源于绝对值算子并且由唯一的微分方程所控制。相较于Ⅰwan 模型，Bouc-Wen模型计算效率较高。Lacey团队研究了不同表面光滑度的钢材料进行螺栓连接时的初滑移系数及初始刚度（Laceya et al.， 2023）。该结构伴随着滞回现象的同时还存在着一些其他的残余刚度特性（Mayergoyz， 1986）。本文将讨论用Bouc-Wen模型描述和预估螺栓连接结构准静态滞回响应曲线的潜力，以及残余刚度的来源因素。

在螺栓模型校正相关研究中，常常使用准静态位移荷载，得到相关的滞回响应力。基于该滞回响应数据，开展参数辨识。常用的参数识别方法有：高斯-牛顿法（Yar et al.，1987）、最小二乘法（Sues， 1988）、简化梯度法（Zhang et al.， 2002）、遗传算法（Kwok et al.， 2007）等。常用的群算法具有较高的计算需求，神经网络拟合需要建立复杂的网络且实现程度较为繁琐。而本文将采用响应灵敏度方法（Lu et al.， 2017）对Bouc-Wen 模型螺栓连接结构的准静态实验数据进行参数识别。

结合ABAQUS 螺栓搭接结构三维有限元仿真（Ⅴaina et al.， 2023），本文评估了Bouc-Wen 模型的螺栓连接表征能力；开展准静态实验研究，验证所提方法的有效性。并通过仿真与物理实验，对实验存在的刚度残余现象进行了力学机理分析。

1 Bouc-Wen模型

Bouc-Wen模型（Chang et al.， 2016）是目前应用广泛的滞回模型，它通过a参数表现各类软化、硬化以及接近双线性的现象（Guo et al.， 2008）。根据等效归一化Bouc-Wen 模型（Pellecchia et al.，2021），有

其中ż表示滞回力变化的快慢；ẋ为滑移的相对速度；a= [A，γ，β，n] 为无量纲滞回环参数，影响滞回环的形状和大小。相比Ⅰwan 模型，Bouc-Wen模型本身是一个半物理半数学的模型，其参数对滞回响应曲线的影响有：1）参数A表征滞回曲线原点处刚度，二者呈现正相关；2）参数γ的增加会使得滞回曲线整体以原点为中心顺时针旋转，如图1 所示；3）参数β表征模型弹性非线性的本构关系，能量耗散大小随β的增加而增加，如图2所示；4）参数n表征弹性-塑性程度，n值越小，滞回曲线越平滑（Yang et al.，2022），如图3所示。

图1 参数γ对迟滞环的影响Fig.1 The influence of γ on hysteresis loop

图2 参数β对迟滞环的影响Fig.2 The influence of β on hysteresis loop

图3 参数n对迟滞环的影响Fig.3 The influence of n on hysteresis loop

因此，Bouc-Wen模型与Ⅰwan模型的滞回响应曲线具有相似性，且具备表征螺栓连接结构的能力。

2 螺栓滞回参数识别

利用三维有限元仿真，本文讨论了Bouc-Wen模型的拟合能力。为此，建立关于螺栓连接结构参数辨识的目标函数。

2.1 目标函数

参数识别问题可归结为一个非线性最小二乘优化问题，即寻找参数a∈Rm，使得

其中B为待识别参数的可行域；i= 1，2，3，…，n即螺栓连接结构滞回响应实验数据；R(a) =[z(xi) ∈Rq]，i= 1，2，3，…，n为求解微分方程（1）后得到的理论解；为权重矩阵W的加权范数。

2.2 增强响应灵敏度方法

非线性目标函数可以使用迭代法进行求解，其关键在于通过已知参数aˉ来确定一个合适的迭代更新量δa，使得g(+δa)尽可能的小。将̂在aˉ的领域进行一阶Taylor展开并忽略高阶项，得

其中

其中

线性化后的目标函数往往是非适定的，此时需要引入Tikhonov正则化处理，即

其中λ≥0 为正则化参数。增量具有以下求解表达式

其中I为单位矩阵。λ≥0 为正则化参数，其值直接关系到不同的更新量δaλ，本文采用L 曲线法确认正则化参数λ，记为.

为了获取合理的迭代更新量，引入置信域限制，使得更新步长‖ ‖δa应该尽可能地小。为了衡量该更新步长是否合适或足够小，需引入一致性指标，使式（9）中的迭代增量满足

由此保证线性化后的目标函数与原目标函数足够接近。由上式可知，合理增大正则化参数会使更新步长足够地小，满足置信域限制，因此该正则化也被称为增强的正则化。

3 算例研究

3.1 有限元准静态实验仿真

螺栓连接结构在承受准静态荷载时，可以模拟成单个Bouc-Wen 模型承受位移激励。螺栓连接结构尺寸如图4 所示（Abad et al.，2014），在ABAQUS 平台上对螺栓连接结构开展有限元仿真，其模型如图5所示。

图4 实验钢板元件尺寸Fig.4 Experimental steel plate element dimensions

图5 有限元仿真模型Fig.5 Finite element simulation model

螺栓连接结构的材料密度为7 830 kg/m3，杨氏模量为2.07 × 1011Pa，法向表面接触摩擦系数为0.3。使用预紧力3 000 N的M12六角头螺栓连接两块板，如图5（b）所示施加螺栓预紧力。如图5（c）所示，其接触-摩擦界面的切向特性为库伦摩擦且最大弹性滑移量设置为特征面尺寸的0.01 %；法向刚度采用允许一个物体的表面穿透到另一个物体的罚函数设置方法。该ABAQUS 设置可以准确求解接触-摩擦界面所产生的滞回曲线，且提供收敛速度。当循环载荷下位移幅值为0.1 mm 时，螺栓连接部位的滞回响应如图6（a）所示。

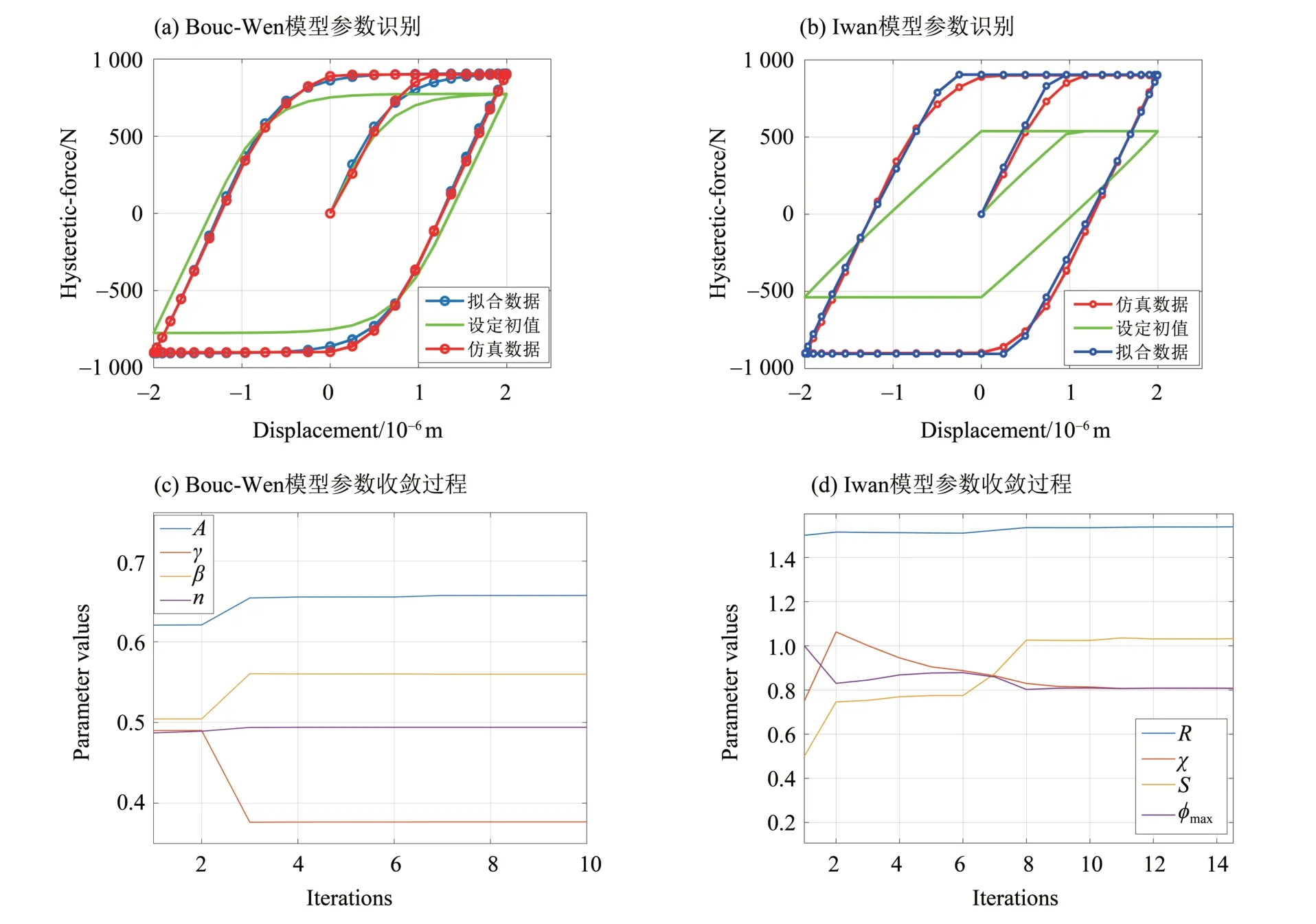
图6 Bouc-Wen、Ⅰwan模型的参数识别与收敛过程Fig.6 The parameter identification and convergence procedure of Bouc-Wen and Ⅰwan model

考虑Bouc-Wen 与四参数Ⅰwan 模型，使用所提响应灵敏度方法对仿真模型开展参数辨识。由于模型参数之间的量级相差较大，引入归一化方法对参数进行预处理。Bouc-Wen 与Ⅰwan 模型的归一化矩阵为IB=diag(2×109，2×103，2×103，4) ，II= diag(1 × 109，1，1 × 109，1 × 10-6).参数识别结果如表1-2所示。

表1 Bouc-Wen参数识别结果Table 1 Bouc-Wen parameter identification results

表2 Ⅰwan参数识别结果Table 2 Ⅰwan parameter identification results

基于识别结果，绘制滞回曲线，如图6 所示。结果表明，Bouc-Wen 和Ⅰwan 模型都能够准确的表征螺栓连接所带来的接触摩擦滞回能量耗散特性。然而，当连接界面从粘滞向滑移状态转变时，如图6（a）左上角和右下角所示，Bouc-Wen 模型的辨识结果可以充分表征该特性。因此，本文所提方法可以准确地从率无关角度对螺栓连接模型开展参数校准。图6（c）和6（d）进一步阐述了参数收敛过程。Bouc-Wen、Ⅰwan 模型的迭代收敛步数分别为7、11 次，然而所需时间分别是2.378 3、271.153 s。这是因为Ⅰwan 模型由一系列的强非线性Jenkins单元并联组合而成，容易产生刚性方程，需要较大计算资源。而Bouc-Wen 模型仅由单自由度微分方程控制，具有较高的计算效率。综上所述，本文所提的基于Bouc-Wen 模型和响应灵敏度的螺栓连接模型参数辨识方法具有准确、高效的特性，能够很好地表征连接界面的接触摩擦滞回能量耗散特性。

3.2 螺栓搭接结构物理实验

3.2.1 实验设计采用304 不锈钢制作与仿真模型一致的螺栓搭接构件。使用扭力扳手对M12 螺栓施加65 N·m 扭矩，将构件连接在一起。使用Ⅰnstron8801 伺服液压机施加简谐位移激励，并测量连接界面所产生的接触摩擦滞回力。在小幅度位移加载下，螺栓与圆孔内壁不会产生接触。考虑正弦位移响应幅值分别为0.1、0.15 mm 时的滞回响应。本文将对0.15 mm 时的位移响应数据开展参数辨识，然后基于该辨识结果校准0.1 mm 的位移响应数据。

3.2.2 参数辨识图7（a）所示实验滞回响应曲线中的微观滑移段落存有一定的斜率，即残余刚度K1.通过求解滞回响应曲线粘滞-滑移与滑移-粘滞转换点之间的斜率，得K1= 2.826 × 107N/m。考虑螺栓连接结构所产生的残余刚度，Bouc-Wen 模型的表达式改写为

图7 基于Bouc-Wen模型的计算拟合与数据预测Fig.7 Computational fitting and data prediction based on Bouc-Wen model

基于本文响应灵敏度方法，对位移幅值为0.15 mm 的实验数据开展参数辨识，参数结果如表3 所示，响应曲线如图7（a）所示。使用识别到的4个参数，对另一组数据（幅值为0.1 mm）的滞回曲线进行预测，其结果如图7（b）所示。在微观滑移段落，由于实验产生的结构磨损及螺栓松动等原因，预测曲线与实验曲线存在一定的偏移，误差处于可以接受的范围；在宏观滑移段落的拟合效果良好，误差较小。结果表明，所识别参数可以很好地拟合实验曲线。

表3 响应幅值为0.15 mm时实验数据的参数识别Table 3 Experimental data parameter identification when response amplitude is 0.15 mm

由于滞回曲线所围成的面积表征了该加载-卸载过程中能量的损耗，计算预测曲线面积与实验数据面积的残差和比值。对响应幅值为0.15 mm 的实验数据识别结果，开展耗散性能分析。有

式中S1是基于实验数据的滞回耗散能力，S2是基于参数辨识曲线的滞回耗散能力。分析可知，β小于10%，表明预测曲线的能量损耗与原数据的能量损耗的误差较小。所提参数识别方法所识别的Bouc-Wen 模型参数，可以真实地反应螺栓搭接结构的滞回曲线响应。

3.3 仿真与实验数据对比

有限元仿真的滞回曲线数据来源于两个钢板连接界面的接触摩擦力，而实验中输出的滞回力的监测点位于钢板的两端，其中包含了螺栓、螺帽处的接触面所产生的接触摩擦。实验前后螺栓和钢板单元均发生了一定程度的沿预紧力方向的变形、磨损。残余刚度很可能来源于螺帽对钢板施加的摩擦力。

对有限元模型开展变形分析，如图8所示，预紧力的施加使得钢板与螺帽接触的部分发生了较为明显的挤压形变。实验和有限元仿真表明，由于钢板单元与螺栓、螺母受预紧力发生了变形，由此导致两者的接触关系不仅存在摩擦力，同时还伴有变形后的残余力。因此，螺栓连接部位在正常服役状态下，其残余刚度来源之一为螺栓、螺母接触面处。

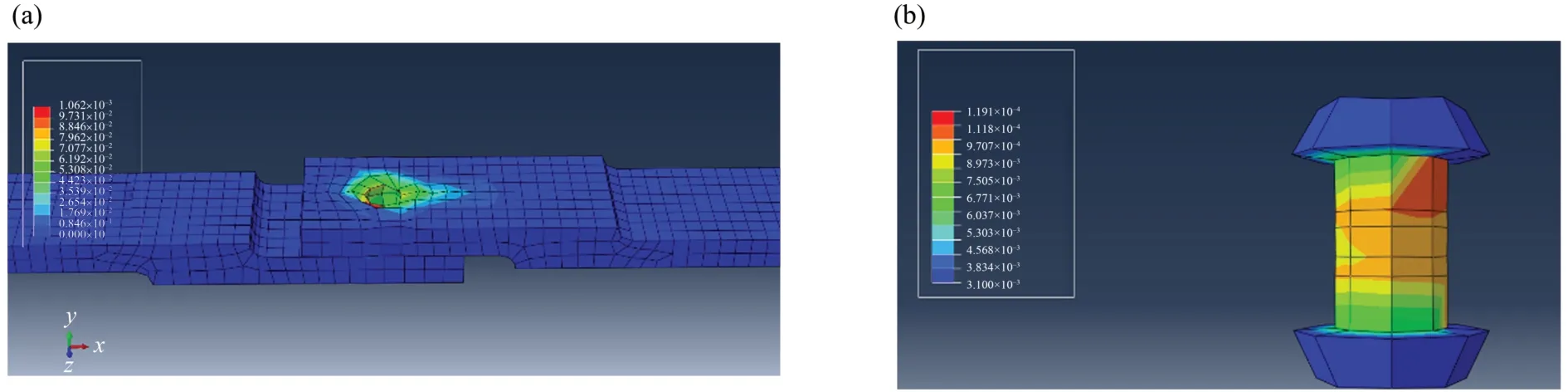
图8 形变的有限元仿真Fig.8 Finite element simulation of deformation

除了残余刚度外，仿真与实验的滞回响应曲线也存在一定差异。这是因为在进行仿真时，所设定的接触面摩擦因数恒为0.3，而实际实验中的摩擦系数未知。对于两种不同的响应幅值情况，本文所提方法对有限元仿真、物理实验都实现了准确的螺栓连接参数辨识。这也说明本文所提方法具有较强的鲁棒性。

4 总 结

本文通过有限元仿真和准静态实验研究，对螺栓搭接结构的接触摩擦、滞回能量耗散进行了研究。结果表明：

（1）本文基于Bouc-Wen 模型，提出了一种响应灵敏度方法，对螺栓连接结构仿真模型、准静态实验数据进行了参数识别，成功预测了不同荷载下的响应。所提方法具有较高效率和准确性。

（2）通过有限元仿真和准静态实验研究，在螺栓预紧力作用下，平板与螺母、螺帽等接触部位发生凹陷变形。在切向振动作用下，螺母、螺帽会发生磨损。在宏观层面上，该特性表现为残余刚度。

（3）与Ⅰwan 模型相比，Bouc-Wen 模型不仅可以有效地表征切向振动下的螺栓搭接结构模型，而且具有计算效率高、非线性强度弱等特点。