双轴应变调控下单层双面神结构MoSSe拉曼光谱的理论研究

孙薇，孙鸿智，赵波，郭怀红

双轴应变调控下单层双面神结构MoSSe拉曼光谱的理论研究

孙薇，孙鸿智，赵波，郭怀红

（辽宁石油化工大学 理学院，辽宁 抚顺 113001）

双轴应变； 拉曼光谱； 单层双面神结构； 应力表征

自2004年石墨烯被成功剥离以来，二维材料，尤其是二维过渡金属硫化物，由于其在机械、光学、电子等领域表现出新奇的物理特性而引起了科学界的广泛关注[1⁃12]。与电场调控手段相比，通过应变调控手段更容易实现对过渡金属硫化物材料的电子特性、光学特性的调控[13⁃17]。据文献[2]报道，单轴、双轴应变可以实现过渡金属硫化物的半导体⁃金属的转变。B.AMIN等[18]通过改变衬底晶格参数，对过渡金属硫化物（TMDC）施加了压应变、拉应变。结果表明，施加压应变、拉应变前后，过渡金属硫化物的能隙、有效质量和载流子迁移率等电子特性都发生了明显变化。S.D.GUO等[19]基于第一性原理计算方法，研究了单层双面神结构过渡金属硫化物的电子结构、传输特性与双轴应变的相关性。综上所述，过渡金属硫化物的基本物性及应力效应研究具有重要的意义。

2017年，A.Y.LU等[20]、J.ZHANG等[21]使用化学气相沉积法制备单层MoSSe，然后使用远程氢等离子体法将S原子替换为H原子。在不破坏真空的情况下，热硒化使Se原子取代H原子，形成结构稳定的单层双面神结构MoSSe。单层双面神MoSSe结构中Mo原子与6个相邻的S/Se原子结合形成六方晶格结构。该结构通过用Se层取代单层MoS2中的一个S层，打破原有的沿垂直于平面外方向的镜像对称性，降低晶体的整体对称性（空间对称群从3h降为3v）。由于单胞中存在上下层Se原子和S原子之间的电负性差，因而产生额外的垂直方向的电偶极场，出现压电性以及增强的光催化、Rashba分裂、二次谐波产生的大压电效应、拓扑等新奇现象[22⁃23]。

通常通过透射电子显微镜技术及高能光谱等实验技术提供材料的结构和电子信息。但是，上述方法存在对材料的要求苛刻、耗时长等问题，甚至会出现破坏材料本身的结构及电子结构特性等问题。拉曼光谱可完全规避上述实验方法的缺点，实现对材料结构、声子结构甚至是电子结构的快速、无损、精准表征。因此，拉曼光谱法被广泛应用于石墨烯及过渡金属硫化物的层数、堆垛方式、边缘方向、掺杂、晶向和应变效应等多方面的研究[2]。但是，针对双面神结构材料进行的拉曼实验研究有限，而且需要进行进一步的理论研究才能更好地诠释实验结果；需要建立双面神结构材料的应力表征标准，才能更好地对实验进行解读。

单轴应变和双轴应变在现实中都很常见，因此对应变进行研究时原则上都需要加以考虑。但是，基于二维材料在电子器件方面的应用，以及单轴应变和双轴应变的特点，本文采用第一性原理，研究双轴应变对单层双面神结构MoSSe的原子结构、电子结构、拉曼光谱特征峰的影响，并系统地讨论了双轴应变调控下振动模式的变化规律，以期辅助拉曼光谱快速、无损、准确地表征单层双面神结构MoSSe材料的应变。

1 计算方法

本文中的结构优化、电子和声子结构计算都是基于密度泛函理论的Quantum Espresso软件包进行的[24]。在计算过程中，使用带有模守恒势的平面波基矢。电子间的交换关联能量泛函中使用的近似是局域密度近似（LDA）。离子⁃电子相互作用采用投影缀加波（PAW）描述[25]。平面波基矢的能量截断为80 Ry（1 Ry=13.605 692 3eV），力和能量收敛分别为5×10-2eV/nm和10-8Ry。根据Monkhorst⁃Pack方法[26]，对布里渊区的点设置11×11×1。为了避免层间相互作用，沿方向设置了2 nm的真空层。通过密度泛函微扰理论计算，获得力常数矩阵（Hessian矩阵）和相应的动力学矩阵，再将相应的动力学矩阵对角化，得到声子谱。

双/单轴应变的计算式见式（1）。

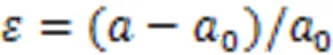
式中：0、分别为应变前、应变后的晶格常数，nm。的正负值分别对应单层结构的拉应变和压应变。需要指出的是，文中所取的应变为－3%～3%，是考虑到在实验测试中容易获取。通过单/双层的纳米压痕等方法，单层石墨烯的双轴拉伸甚至可高达25%。

计算双轴应变下的单层双面神结构MoSSe结构时，六方晶格以特定的比例均匀放大至3%，或均匀缩小至－3%，同时允许所有的原子充分弛豫。通过这种方式，布里渊区除了尺寸发生变化，仍可保持完美的六边形形状。

2 结果和讨论

2.1 单层双面神结构 MoSSe的结构

单层双面神结构 MoSSe是六方晶格结构，Mo原子与6个相邻的S/Se原子结合，其原子结构如图1所示。

2.2 单层双面神结构MoSSe振动模式的对称性分析

对单层双面神结构MoSSe进行了对称性的群论分析，结果见表1—2。表中第一行的、23和3分别表示群元素的操作类，其中3和前面的数字表示该类操作的阶，表示属于该类对称操作的数目，也就是说，属于3对称操作的有2个，属于对称操作的有3个。其中，红外活性的晶格振动模由红外光谱表示，拉曼活性的晶格振动模由拉曼光谱表示。

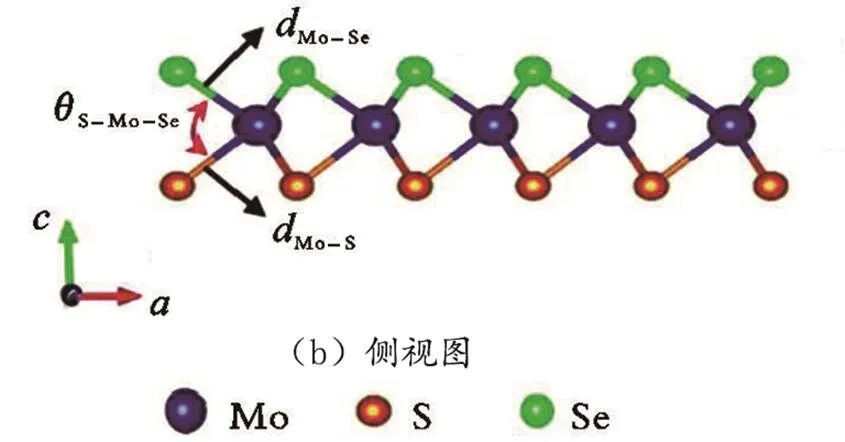
图1 单层双面神结构MoSSe

表1 单层双面神结构MoSSe所属C3v点群的特征标表

表2 单层双面神结构MoSSe所属C3v点群的对称分析结果

由表1—2可知，单层双面神结构MoSSe所属的3v点群含有包括3度转动、垂直镜面等3个对称操作及3个不可约表示：1、2和。进行对称操作后，所产生的不动原子数的可约表示为as，三维直角坐标的变换矩阵迹的可约表示为vec；晶格振动的可约表示为vib，vib可以写成前2个可约表示的直积，即vibas􀱋vec。对vib进行不可约分解，可得：vib3+31。减去3个平移对称操作的不可约表示（1），便可得单层双面神结构MoSSe中所有6个光学振动模式2+21。

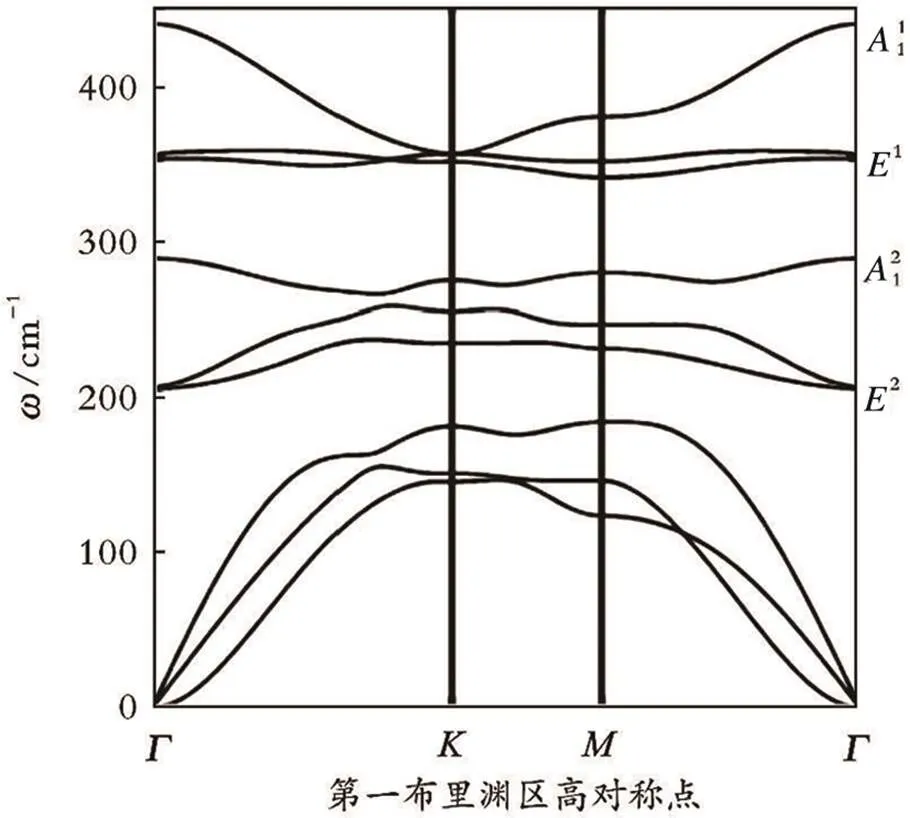
图2 单层双面神结构MoSSe的声子色散图

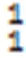
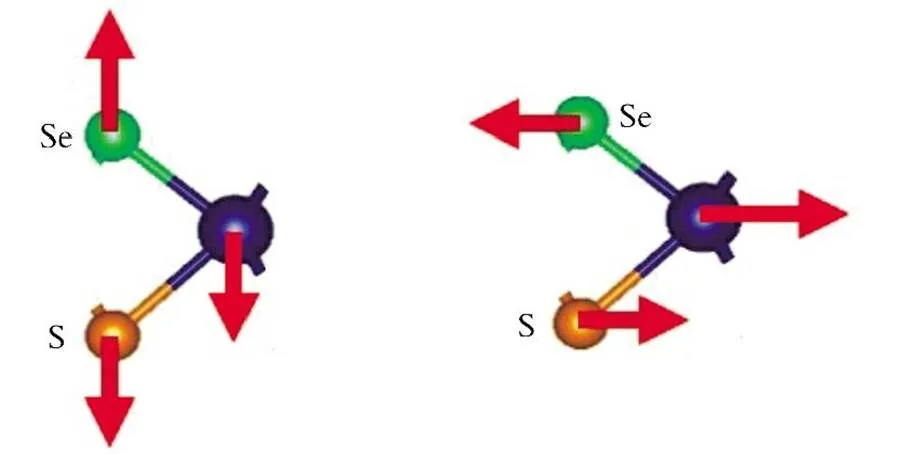
图3 单层双面神结构MoSSe在第一布里渊区中心点的拉曼活性光学模的振动模式

Fig.3 Raman⁃active optical modes of Janus MoSSe single⁃layeratpoint in the center of the first Brillouin Zone

2.3 双轴应变下的拉曼光谱

讨论了双轴应变对单层双面神结构MoSSe的拉曼光谱的作用，以及原子结构、电子结构的相应变化。

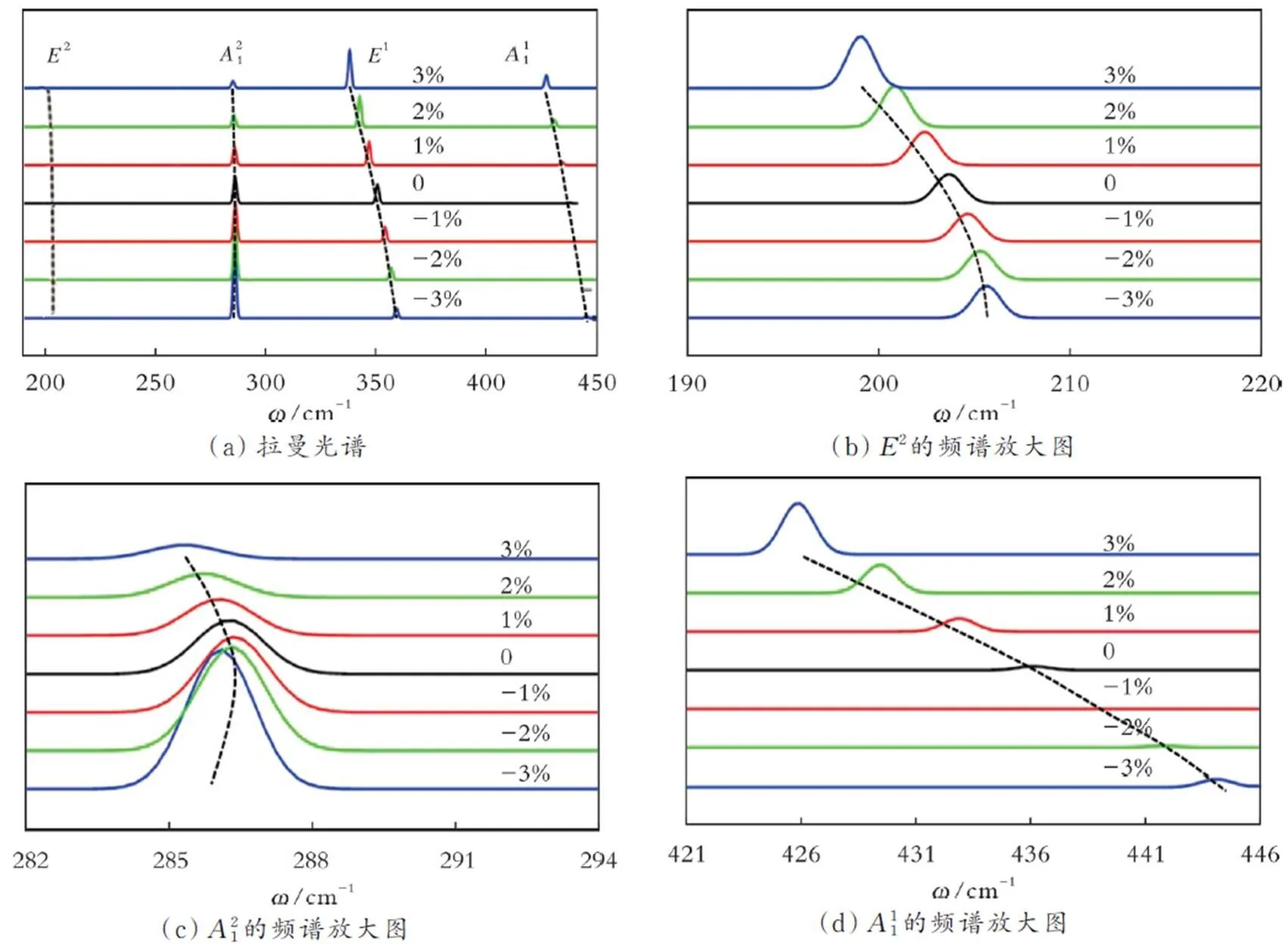
图4 双轴应变下的单层双面神结构MoSSe的拉曼光谱以及E2、A、A的频谱放大图

在双轴应变下，单层双面神结构MoSSe也出现了面外振动模的拉曼峰强随应变的变化出现极小值的情况，与前期研究发现的二维过渡金属硫化物材料中普遍存在的面外振动模式强度极小的现象相似，导致该现象的原因是该材料的介电常数对应变并不敏感[22]。与单层二维过渡金属硫化物材料不同的是，在双轴应变下，单层双面神结构MoSSe的面外振动模的拉曼强度极小值出现在压应变区域。这种差异应该来自应变引起的介电系数或电磁屏蔽能力的变化。单层过渡金属硫化物材料中拉应变引起能带能隙的快速减小，增强介电屏蔽能力，因此降低介电对应变的敏感度，造成拉曼强度的降低[7⁃8]。同理，在单层双面神过渡金属硫化物中，如果压应变也会造成能隙的快速减小，则拉曼强度的最小化也是可以理解的。

（a）拉曼频率 （b）拉曼强度

图5 双轴应变下的单层双面神结构MoSSe的4个拉曼光谱模的拉曼频率和拉曼强度随应变的变化曲线

Fig. 5 Bi⁃axial strain dependence of frequency and intensity of four Raman modes of Janus MoSSe single⁃layerat

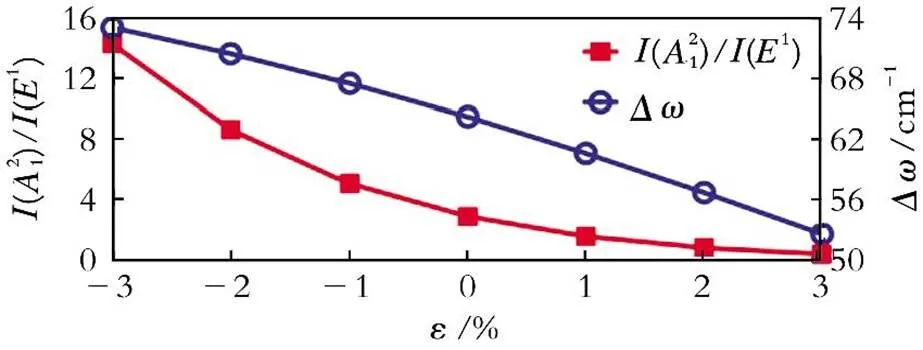
图6 单层双面神结构MoSSe的拉曼振动模式E1与A的拉曼频率差(Δω)及强度比(I(A)/I(E1)）随应变的变化曲线

2.4 双轴应变下的电子能带结构和晶胞参数

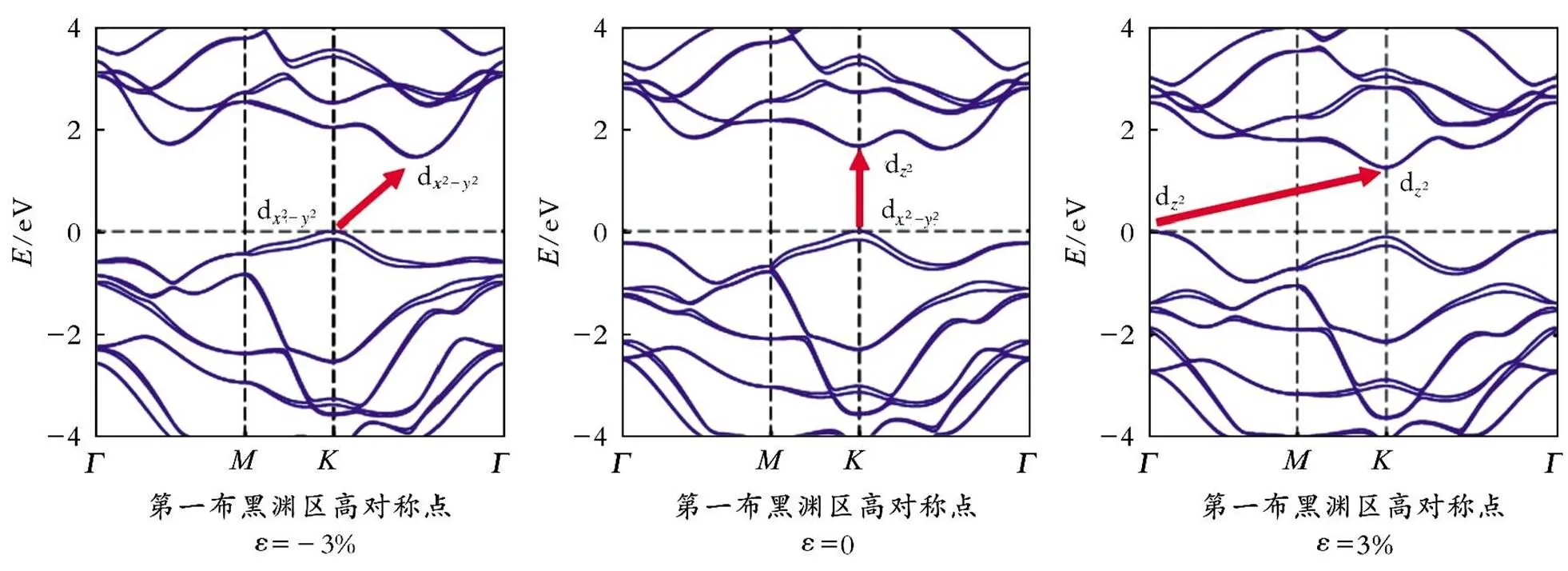
（a）电子能带结构

（b）态密度分波（DOS）

图7 不同应变下单层双面神结构MoSSe的电子能带结构和态密度分波（DOS）

Fig.7 Electron band structure and density of states (DOS) of Janus MoSSe single⁃layerat under different strains

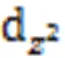
单层双面神结构MoSSe的能隙g与应变的关系曲线如图8所示。从图8可以看出，间接带隙大小随拉应变和压应变的增加而单调减小，不过能隙对拉应变比对压应变的响应更敏感。

与单层过渡金属硫化物在一定的压应变下出现能隙最大值不同[23]，单层双面神结构MoSSe的能隙最大值出现在零应变处。这意味着无论是拉应变还是压应变，能隙快速减小会增强介电常数或电磁屏蔽能力，相应地减弱介电常数对应变的响应敏感度，引起拉曼强度的降低。

图8 单层双面神结构MoSSe的能隙Δg与应变ε的关系曲线

应变下能带的变化趋势与晶胞参数密切相关。绘制了单层双面神结构MoSSe的键长、键角与应变的关系曲线，结果如图9所示。由图9可以看出，无论是压应变还是拉应变，Mo—S、Mo—Se的键长随应变的变化规律与S—Se的键长变化规律完全相反。由此可知，单层双面神结构MoSSe无论是压应变还是拉应变都具有正的泊松比。

（a）（b）

图9 单层双面神结构MoSSe的晶胞参数（、）与应变的关系曲线

Fig. 9 Straindependence of cell parameters（,） of Janus MoSSe single⁃layerat

2.5 偏振拉曼光谱的特征峰

从单层双面神结构MoSSe的几个振动模式的拉曼张量出发，获取线偏振激光激发下拉曼峰强的角度，以及圆偏振光下的选择定则，为可能的实验研究提供一定的理论指导。

振动模的不可约表示和1，分别具有如下的拉曼张量形式：

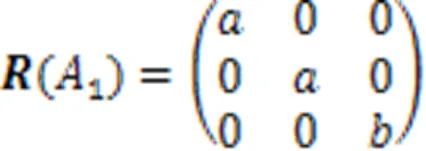
式中：、、、、均为张量元。

拉曼强度（）与张量、入射激光偏振矢量i和散射激光偏振矢量s相关，即：

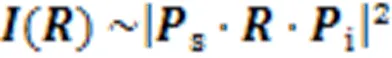
在线偏振情形下，通过式（4）进行计算不难发现，在入射光和散射光的偏振矢量相互平行（例如，i=s=（cos，sin，0））或相互垂直（例如，i=（cos，sin，0），s=（-sin，cos，0））的情况下，所有模式的拉曼强度都与偏振矢量的角度无关（例如，当i∥s时，(1)～2，()～2；当i⊥s时，(A1)=0，(E)～2），这与材料平面内的各向同性不无关系。值得注意的是，当入射光和散射光的线偏振矢量垂直时，1模式的拉曼强度消失，这个偏振设置可用于判断1模式。

与单层过渡金属硫化物的情况类似[24]，在圆偏振情形下，和1模式分别在入射光和散射光的偏振矢量相互垂直和相互平行设置下出现非零强度，即在i∥s时，（i，s）=（+，+）或（-，-），(1)=42≠0，()=0；而在i⊥s时，（i，s）=（+，-）或（-，+），(1)=0，()=42≠0。其中，+和-分别对应于左旋和右旋的圆偏振极化的Jones矢量，±=(1，±i，0)（i为虚数）。当然，由于双面神结构中存在垂直平面方向的电偶极化，除了形变势的电声耦合，Frolich型的电声耦合也会产生作用，从而产生所谓的反常选择定则[25]，例如，在（i，s）=（+，+）或（-，σ-）时，出现()≠0。

3 结 论

系统地研究了双轴应变对单层双面神结构MoSSe的晶格结构、电子结构和拉曼光谱的影响。结果表明，在双轴应变的作用下，单层双面神结构MoSSe表现出从直接到间接的带隙转换。双轴应变使其能带结构改变的根本原因在于导带底和价带顶电子轨道组合成键能量的相对变化。

通过简单建模，针对具有普遍性和特殊性的应变效应进行了梳理。结果表明，由于单层双面神结构MoSSe的面内结构是各向同性的，因此其偏振拉曼谱与单层过渡金属硫化物相似，但是存在更强的电偶极子，可能存在更强的圆偏振反常拉曼信号，期待实验证实。

研究结果表明，基于特征峰频率和强度随应变的变化差异，可以通过特征峰之间的频率差和强度比快速、准确、无损地定量化双面神结构材料的应变类型及其大小。

［1］ RIVERA P，SCHAIBLEY J R，JONES A M，et al.Observation of long⁃lived interlayer excitons in monolayer MoSe2⁃WSe2heterostructures［J］.Nature Communications，2015，6（1）：6242.

［2］ 郭怀红，赵波.拉曼光谱探究二维原子晶体结构和物性的研究进展［J］.辽宁石油化工大学学报，2018，38（6）：1⁃9.

GUO H H，ZHAO B. Research progress of Raman spectroscopy in exploring structural and physical properties of two dimensional atomic crystal［J］. Journal of Liaoning Shihua University，2018，38（6）：1⁃9.

［3］ FARKOUS M，BIKEROUIN M，PHUNG H T T，et al.Electronic and optical properties of layered van der Waals heterostructure based on MS2（M=Mo，W） monolayers［J］.Materials Research Express，2019，6（6）：065060.

［4］ XIA C X，XIONG W Q，DU J，et al.Universality of electronic characteristics and photocatalyst applications in the two⁃dimensional Janus transition metal dichalcogenides［J］.Physical Review B，2018，98（16）：165424.

［5］ CAI H F，GUO Y F，GAO H J，et al.Tribo⁃piezoelectricity in Janus transition metal dichalcogenide bilayers：A first⁃principles study［J］.Nano Energy，2019，56：33⁃39.

［6］ KANDEMIR A，SAHIN H.Bilayers of Janus WSSe：Monitoring the stacking type via the vibrational spectrum［J］.Physical Chemistry Chemical Physics，2018，20（25）：17380⁃17386.

［7］ LEE C，YAN H G，BRUS L E，et al.Anomalous lattice vibrations of single⁃and few⁃layer MoS2［J］.ACS Nano，2010，4（5）：2695⁃2700.

［8］ Molina⁃Sánchez A，WIRTZ L.Phonons in single and few⁃layer MoS2and WS2［J］.Physical Review B，2011，84（15）： 155413.

［9］ ZHU Z Y，CHENG Y C，SCHWINGENSCHLÖGL U.Giant spin⁃orbit⁃induced spin splitting in two⁃dimensional transition⁃metal dichalcogenide semiconductors［J］.Physical Review B，2011，84（15）：153402.

［10］ HUANG J Q，LIU Z Y，YANG T，et al.New selection rule of resonant Raman scattering in MoS2monolayer under circular polarization［J］.Journal of Materials Science & Technology，2022，102：132⁃136.

［11］ ZHAO Y，ZHANG S S，SHI Y P，et al.Characterization of excitonic nature in Raman spectra using circularly polarized light［J］.ACS Nano，2020，14（8）：10527⁃10535.

［12］ 孙鸿智，孙薇，赵波，等.单层Janus MoSSe双共振拉曼散射的理论研究［J］.辽宁石油化工大学学报，2022，42（3）：30⁃36.

SUN H Z，SUN W，ZHAO B，et al. Theoretical study on double resonant Raman scattering in Janus MoSSe monolayer［J］. Journal of Liaoning Petrochemical University，2022，42（3）：30⁃36.

［13］ MOHIUDDIN T M G，LOMBARDO A，NAIR R R，et al.Uniaxial strain in graphene by Raman spectroscopy：peak splitting，Grüneisen parameters， and sample orientation［J］.Physical Review B，2009，79（20）：205433.

［14］ JOHARI P，SHENOY V B.Tuning the electronic properties of semiconducting transition metal dichalcogenides by applying mechanical strains［J］.ACS Nano，2012，6（6）：5449⁃5456.

［15］ BERTOLAZZI S，BRIVIO J，KIS A.Stretching and breaking of ultrathin MoS2［J］.ACS Nano，2011，5（12）：9703⁃9709.

［16］ LIU H T，HUANG Z Y，HE C Y，et al.Strain engineering the structures and electronic properties of Janus monolayer transition⁃metal dichalcogenides［J］.Journal of Applied Physics，2019，125（8）：082516.

［17］ ZHANG Y，GUO H H，SUN W，et al.Scaling law for strain dependence of Raman spectra in transition⁃metal dichalcogenides［J］.Journal of Raman Spectroscopy，2020，51（8）：1353⁃1361.

［18］ AMIN B，KALONI T P，SCHWINGENSCHLÖGL U.Strain engineering of WS2，WSe2，and WTe2［J］.RSC Advances， 2014，4（65）：34561⁃34565.

［19］ GUO S D，DONG J.Biaxial strain tuned electronic structures and power factor in Janus transition metal dichalchogenide monolayers［J］.Semiconductor Science and Technology，2018，33（8）：085003.

［20］ LU A Y，ZHU H Y，XIAO J，et al.Janus monolayers of transition metal dichalcogenides［J］.Nature Nanotechnology，2017， 12（8）：744⁃749.

［21］ ZHANG J，JIA S，KHOLMANOV I，et al.Janus monolayer transition⁃metal dichalcogenides［J］.ACS Nano，2017，11（8）： 8192⁃8198.

［22］ JI Y J，YANG M Y，LIN H P，et al.Janus structures of transition metal dichalcogenides as the heterojunction photocatalysts for water splitting［J］.The Journal of Physical Chemistry C，2018，122（5）：3123⁃3129.

［23］ LI F P，WEI W，ZHAO P，et al.Electronic and optical properties of pristine and vertical and lateral heterostructures of Janus MoSSe and WSSe［J］.The Journal of Physical Chemistry Letters，2017，8（23）：5959⁃5965.

［24］ GIANNOZZI P，BARONI S，BONINI N，et al.QUANTUM ESPRESSO：A modular and open⁃source software project for quantum simulations of materials［J］.Journal of Physics：Condensed Matter，2009，21（39）：395502.

［25］ BLÖCHL P E.Projector augmented⁃wave method［J］.Physical Review B，1994，50（24）：17953.

［26］ MONKHORST H J，PACK J D.Special points for Brillouin⁃zone integrations［J］.Physical Review B，1976，13（12）：5188.

Theoretical Study on Raman Spectra of Janus MoSSe Single⁃Layer under Bi⁃Axial Strain

SUN Wei， SUN Hongzhi， ZHAO Bo， GUO Huaihong

（College of Sciences，Liaoning Petrochemical University，Fushun Liaoning 113001，China）

Biaxial strain； Raman spectroscopy； Janus monolayer； Strain characterization

O482.31

A

10.12422/j.issn.1672⁃6952.2024.01.006

2023⁃03⁃21

2023⁃04⁃30

辽宁省教育厅面上项目（LJKZ0391）。

孙薇（1996⁃），女，硕士研究生，从事低维材料物性方面的研究；E⁃mail：sunwei_961109@163.com。

郭怀红（1980⁃），女，博士，副教授，从事低维材料物性调控方面的研究；E⁃mail：hhguo@alum.imr.ac.cn。

孙薇,孙鸿智,赵波,等.双轴应变调控下单层双面神结构MoSSe拉曼光谱的理论研究[J].辽宁石油化工大学学报,2024,44(1):35-42.

SUN Wei,SUN Hongzhi,ZHAO Bo,et al.Theoretical Study on Raman Spectra of Janus MoSSe Single⁃Layer under Bi⁃Axial Strain[J].Journal of Liaoning Petrochemical University,2024,44(1):35-42.

（编辑 宋锦玉）