二元广义反码与最优LCD码
李瑞虎, 付 强, 宋 昊, 刘 杨
(空军工程大学基础部,西安,710051)
二元反码是由Farrell[1]首先提出的,反码在小码长最优码构造和局部修复码研究方面得到广泛应用[2-3]。近年来,人们证明线性补对偶(linear complementary dual,LCD)码能够用于经典与量子信息保护、防止侧信道攻击[3-5],从而掀起研究LCD码的热潮[5-15]。研究一般码长的LCD码时,用组合构造、计算机辅助搜索和解方程等方法确定出一些小码长(n≤40)最优LCD码以及维数k≤4的LCD码,但是却难以确定码长超过40的最优LCD码以及维数更大的最优LCD码[6-14]。为突破现有方法的局限性,借鉴文献[17~19]中线性码的定义向量(defining vector)理论,本文引入广义反码及其定义向量、定义向量的重复度概念,确立广义反码、其参数与定义向量之间的联系。利用广义反码描述任意码长线性码的参数,将确定任意码长线性码的参数问题转化为确定小码长广义反码问题。
设Nm=2m-1, 关于二元最优[sNm+Nm-a,m]的LCD性,可得到如下结果:
1)m=3,且a=2时,存在二元最优[sNm+Nm-a,m]码为LCD码[8-10]。
2)m=4,5,6且a=5,9时,存在二元最优[sNm+Nm-a,m]码为LCD码[10-13]。
本文将利用线性码的定义向量和广义反码理论,研究二元最优[sNm+Nm-a,m]的根维数以及LCD性,设法证明1≤a≤11,m适当大时, 二元最优[sNm+Nm-a,m]线性码不是LCD码。
1 基本理论
本文中F2为二元域,线性码C指二元线性码,C的Euclid对偶表示为C⊥,定义为:
若C⊆C⊥,C叫做自正交 (self-orthogonal,SO) 码。Hull(C)=C∩C⊥叫做C的根码[3,15],又称为C的包壳,Hull(C)的维数记为h(C)。
若Hull(C)={0}(或h(C)=0),C叫做线性补对偶码[3]。
若[n,k,d]码存在, 定义:
h([n,k,d])=min{h(C)∣C=[n,k,d]}。
如果存在置换将码C变成C′,C和C′ 称为等价码,C≅C′。若G1与G2生成等价码, 则记为G1≅G2。等价码性能一样,故可以不区分等价码与置换等价的生成矩阵,将它们视作同一对象进行。
约定: 由二维Simplex 码的生成矩阵S2结合递归构造方法,可构造k-维 Simplex的生成矩阵:
记αi为i(1≤i≤N=2k-1) 的二进制k-维向量表示, 即α1=(1,0,…,0)T,…,αN=(1,1,…,1)T, 则Sk=(α1,…,αN)。
记Sk的后2k-2m列(1≤m≤k-1)构成的矩阵为Mk,m,Mk,m生成Mk,m=[2k-2m,k,2k-1-2m-1] MacDonald码[21]。
若G是C=[n,k] 的生成矩阵,G中有li,αi(1≤i≤N),称L=(l1,…,lN)为G的定义向量,并记G为G=(l1α1,…,lNαN)。
设ljl(1≤l≤t)为L=(l1,l2,…,lN)的不同坐标且lj1 例如L1=(s+1,s-1,s,s,s+1,s-1,s+1) 具有类型]](s-1)2∣(s)2∣(s+1)3]],L2=(3,1,1,3,1,3,1) 具有类型]](1)4∣(3)3]]。 设Pk为Sk中全体非零向量为行的(2k-1)×(2k-1)矩阵,Jk为(2k-1)×(2k-1) 全一矩阵,Qk=Jk-Pk。线性码C=[n,k]的距离和性质可由定义向量L=(l1,…,lN)得到。若C=[n,k]具有生成矩阵G=(l1α1,…,lNαN)和定义向量L=(l1,…,lN),WT=PkLT,则W=(w1,w2,…,wN) 对应C中2k-1个非零向量的重量,d=min1≤i≤2k-1{wi}为C最小距离[16-17]。记W=(w1,w2,…,wN)=d12k-1+Λ,其中Λ=(λ1,λ2,…,λN)且λi=wi-d≥0则至少有一个λi=0.设σ=λ1+λ2+…+λN, 则σ=2k-1n-d(2k-1) 。 可由WT=PkLT得到L=(l1,…,lN),由如下方程解出: 引理1.1设C=[n,k,d]的生成矩阵和定义向量分别为G与L,有: 1)若lmin 2) 若k≥3,则GGT=Ga(Ga)T; 3)C为LCD码当且仅当Ga(Ga)T可逆。 证明1)从sSk中删除G的列得到Ga,sSk生成等重码[s(2k-1),k,s2k-1],而Ga中行的2k种线性组合向量的最大重量为δ,故d=s2k-1-δ。 GGT=Ga(Ga)T 3)C为LCD码当且仅当GGT可逆,由(2)可得C为LCD码当且仅当Ga(Ga)T可逆。 下文要用到C的约化码和扩展码的h(C)[15]。 引理1.2[15]若C1为C的约化码,h(C1)=h≥2, 则h(C)≥h-1≥1,C不是LCD码。 引理1.3[15]设d为奇数,Ce为C=[n,k,d]的扩展码,若h(Ce)=h≥2,则h(C)≥h-1≥1,C不是LCD码。 本文的主要结论如下: 定理1.1设s≥0,Nk=2k-1,1≤a≤11.若(k,a)满足条件 :①k≥4,a=1,3,4,7,8;②k≥5,a=2,6,10; ③k≥7,a=5,9,11。则相应条件下二元[sNk+Nk-a,k]最优码不是LCD码。 本节证明引理1.1, 分3步进行:①a=1,3,4,7,8;②a=2,6,10,11;③a=5,9。 引理2.1若s≥0,k≥4 ,Nk=2k-1且a=1,3,4,7,8,则[Nks+Nk-a,k]最优码不是LCD码。 证明设a=1,3,7, 则相应有a=2r-1,其中r分别对应1,2,3。1≤r≤k-1时[18],有: C=[sN+2k-2r,k,s2k-1+2k-1-2r-1] 唯一,C=Ms(k,r)=[sN+2k-2r,k,s2k-1+2k-1-2r-1]是s个Simplex码与MacDonald码的并置;故r对应为1,2,3时C的根维数h(C)分别为k-1,k-2,k。从而C不是LCD码。 当a=4,8时,二元最优[Nks+Nk-a,k]的距离分别为2k-1s+2k-1-3和2k-1s+2k-1-5,这时它们的扩展码分别对应a=3,7的最优码。 由扩展码的根维数可推出a=4,8, 最优码[Nks+Nk-a,k]的根维数分别为k-2≥2以及k,故二元最优[Nks+Nk-a,k]是根维数不小于1的码,不是LCD码。 引理 2.2若k≥5,则二元最优[Nks+Nk-2,k,2k-1s+2k-1-2]码不是LCD码。 证明若k≥5, 记Nk=N, 则C=[n,k,d]=[Nks+Nk-2,k,2k-1s+2k-1-2]为二元最优码。 对此码有σ=2k-1n-d(2k-1)=2k-1+d,且L满足s-1≤li≤s+2,1≤i≤N。 1)若lmax=s+2, 则C有约化码:[Nks+Nk-4,k-1,2k-1s+2k-1-2]=[(2s+1)Nk-1+Nk-1-3,k-1,(2s+1)2k-2s+2k-2-2] 此约化码的h≥(k-1)-2=k-3。故h(C)≥k-4。 2)若lmax=s+1且lmin=s, 则有广义反码(2,2k,{2}),此广义反码(2,2k,{2})的秩为2,因此h(C)≥k-2。 3)若lmax=s+1且lmin=s-1, 则C的定义向量L以及Lc分别具有以下形式: L:]](s-1)1∣(s)0∣(s+1)N-1]], 从而此时C为自正交码,h(C)≥k。 总结以上讨论结果,可得到: h([Nks+Nk-2,k,2k-1s+2k-1-2])≥k-4,引理成立。 引理2.3若k≥5,则二元最优[Nks+Nk-6,k]码不是LCD码。 证明记C=[n,k,d]=[Nks+Nk-6,k,2k-1s+2k-1-4]为二元最优码,对此码有σ=2k-1n-d(2k-1)=2k-1+d, 且L满足s-1≤li≤s+2,1≤i≤N。 1)若lmax=s+2,则C有约化码: [Nks+Nk-8,k-1,2k-1s+2k-1-4]= [(2s+1)Nk-1+Nk-1-7,k-1,(2s+1)2k-2s+2k-2-4] 其为自正交码,因此h(C)≥k-2。 2)若lmax=s+1且lmin=s, 则有广义反码(6,2k,{4}),此广义反码(6,2k,{4})的秩至多为4,故h(C)≥k-4。 3)若lmax=s+1且lmin=s-1, 则C的定义向量L以及Lc分别具有形式: ①L1:]](s-1)1∣(s)4∣(s+1)N-5]], ②L2:]](s-1)2∣(s)2∣(s+1)N-4]], ③L3:]](s-1)3∣(s+1)N-3]]; 以上3种定义向量L分别对应码的h(C)值为h≥k-4,h≥k-2以及h=k。 总结以上各种情况,可得到h([Nks+Nk-6,k,2k-1s+2k-1-4])≥k-4,故引理成立。 引理2.4若k≥7,则二元最优[Nks+Nk-5,k]码不是LCD码。 证明记C=[n,k,d]=[Nks+Nk-5,k,2k-1s+2k-1-4]为二元最优码,σ=2k-1n-d(2k-1)=2×2k-1+d, 且s-2≤li≤s+3,1≤i≤N。 1)若lmax=s+3, 则C有约化码[Nks+Nk-8,k-1,2k-1s+2k-1-4]=[(2s+1)Nk-1+Nk-1-7,k-1,(2s+1)2k-2s+2k-2-4]为自正交码。 因此h(C)≥k-2。 2)若lmax=s+2, 则C有约化码[Nks+Nk-7,k-1,2k-1s+2k-1-4]=[(2s+1)Nk-1+Nk-1-6,k-1,(2s+1)2k-2s+2k-2-4],此约化码的h值为h≥k-1-4=k-5.因此h(C)≥k-6。 3)若lmax=s+1 且lmin=s, 则有广义反码(5,2k,{4}),此广义反码(5,2k,{4})的秩至多为4,故h(C)≥k-4。 4)若lmax=s+1 且lmin=s-1, 则C的定义向量L以及Lc分别具有以下形式: ①L1:]](s-1)1∣(s)3∣(s+1)N-4]], ②L2:]](s-1)2∣(s)1∣(s+1)N-3]], 以上2种定义向量L分别对应码的h(C)值为h≥k-3,h≥k-1。 5)若lmax=s+1 且lmin=s-2,则C的定义向量L以及Lc分别具有形式: ②L2:]](s-2)1∣(s-1)1∣(s)0∣(s+1)N-2]], 以上2种定义向量L分别对应码的h(C)值为h≥k-3,h≥k-1。 总结以上各种情况,可得到h([Nks+Nk-5,k,2k-1s+2k-1-4])≥k-6,故引理成立。 引理2.5若k≥5,则二元最优[Nks+Nk-10,k]码不是LCD码。 证明记[n,k,d]=[Nks+Nk-10,k,2k-1s+2k-1-6], 则C=[n,k,d]为二元最优码,并有σ=2k-1n-d(2k-1)=2k-1+d,且L满足s-1≤li≤s+2,1≤i≤N。 首先, 我们可断言lmax=s+2不会出现,否则C有约化码[Nks+Nk-12,k-1,2k-1s+2k-1-6]=[(2s+1)Nk-1+Nk-1-11,k-1,(2s+1)2k-2+2k-2-6]违背Griesmer界,矛盾。从而可得lmax=s+1。 1)若lmax=s+1,lmin=s,则C对应的反码为(10,2k,{6}),此广义反码生成矩阵Ga的秩至多为6,下面证明Ga的秩至多为5。 否则,可设Ga≅(I6∣u1,u2,u3,u4),ui(1≤i≤4)是互不相同的向量且重量都大于2。 若ui中有一个具有奇重量, 则反码具有码字 的重量δ≥7,矛盾。若ui都具有偶重量,则由4×2/6=2可知(u1,u2,u3,u4)具有一行的重量不小于2,于是Ga中存在5行的线性组合得到的码字重量δ≥7,矛盾。故可得出Ga的秩至多为5。 根据文献[20], 秩不超过5的(10,2k,{6})反码仅有2个,分别满足rank(Ga(Ga)T)=4,2故此种情况下h(C)≥k-4。 2)若lmax=s+1,lmin=s-1,则C的定义向量L以及Lc分别具有形式: ①L1:]](s-1)1∣(s)8∣(s+1)N-9]], ②L2:]](s-1)2∣(s)6∣(s+1)N-8]], ③L3:]](s-1)3∣(s)4∣(s+1)N-7]], ④L4:]](s-1)4∣(s)2∣(s+1)N-6]], ⑤L5:]](s-1)5∣(s)0∣(s+1)N-5]], 若L(Lc)具有形式Li,(3≤i≤5),则有rank(Ga(Ga)T)≤4。 总结上面2种情形,即证明引理成立。 推论2.6若k≥6,则二元最优[Nks+Nk-11,k]码不是LCD码。 证明参数[Nks+Nk-11,k,2k-1s+2k-1-7]的码是二元最优码,它的扩展码是[Nks+Nk-10,k,2k-1s+2k-1-6]二元最优码,此扩展码的根维数h≥k-4。 当k≥6, 扩展码的根维数h≥k-4≥2,故二元最优[Nks+Nk-11,k]码的根维数h≥k-5,不是LCD码。 引理2.7若k≥7,则二元最优[Nks+Nk-9,k]码不是LCD码。 证明记C=[n,k,d]=[Nks+Nk-9,k,2k-1s+2k-1-6]为二元最优码,对此最优码有σ=2k-1n-d(2k-1)=2×2k-1+d,且s-2≤li≤s+3(1≤i≤N)。 仿照引理2.4可证明lmax=s+3不会出现,于是lmax≤s+2。 1)lmax=s+2, 则C有约化码[Nks+Nk-11,k-1,2k-1s+2k-1-6]=[(2s+1)Nk-1+Nk-1-10,k-1,(2s+1)2k-2s+2k-2-6], 此约化码的h值为h≥=k-5,因此h(C)≥k-6。 2)若lmax=s+1,lmin=s,则C的则有广义反码(9,2k,{6}),此广义反码(9,2k,{6})的秩至多为6,故h(C)≥k-6。 3)若lmax=s+1,lmin=s-1,则C的定义向量L以及Lc分别具有形式: ①L1:]](s-1)1∣(s)7∣(s+1)N-8]], ②L2:]](s-1)2∣(s)5∣(s+1)N-7]], ③L3:]](s-1)3∣(s)3∣(s+1)N-6]], ④L4:]](s-1)4∣(s)5∣(s+1)N-5]], 若L(Lc)具有形式Li,(2≤i≤4),则有rank(Ga(Ga)T)≤5。 于是, 我们仅需要确定情形1)下广义反码(9,2k,{6})的秩,仿照情形1)可证明广义反码生成矩阵Ga的秩至多为5。这表明lmax=s+1且lmin=s-1时h(C)≥k-5。 4)若lmax=s+1,lmin=s-2, 则C的定义向量L以及Lcs分别具有形式: ①L1:]](s-2)1∣(s-1)0∣(s)6∣(s+1)N-7]], ②L2:]](s-2)1∣(s-1)1∣(s)4∣(s+1)N-6]], ③L3:]](s-2)1∣(s-1)2∣(s)2∣(s+1)N-5]], ④L4:]](s-2)2∣(s-1)0∣(s)3∣(s+1)N-5]], ⑤L5:]](s-2)2∣(s-1)1∣(s)1∣(s+1)N-4]], ⑥L6:]](s-2)1∣(s-1)3∣(s)0∣(s+1)N-4]], ⑦L7:]](s-2)3∣(s-1)0∣(s)0∣(s+1)N-3]], 总结以上4类情形,即证明引理成立。 本文利用广义反码理论与方法研究形如[sNk+Nk-a,k]的二元性质,证明1≤a≤11,k≥7时,二元最优码不是LCD码。这为确定对应码长最优LCD码的距离以及研究如何构造最优LCD码奠定了基础, 为研究高维二元LCD提供了可借鉴的新理论和新方法。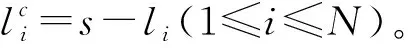
2 定理1.1的证明
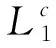
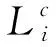
3 结语

