双基地米波MIMO雷达低空目标俯仰维DOD和DOA联合估计方法
王鸿帧,宋玉伟,辛 波,游志远
(1.空军工程大学防空反导学院,西安,710051; 2.93575部队,河北承德,067000;3.93501部队,北京,100010)
近年来,阵列信号处理技术[1]中大量理论创新成果在雷达领域得到广泛应用,空间谱估计[2]作为阵列信号处理技术中的核心问题,相比于单脉冲等传统测向技术,其可突破“瑞利限”从而实现超分辨估计。在阵列信号处理技术发展的同时,双基地雷达因其反隐身、抗干扰和收发分置的优势成为专家学者们的研究热点[3]。将空间估计理论应用到双基地雷达,由此衍生出一个新的研究方向,即双基地雷达波离方向(direction of departure, DOD)和波达方向(direction of arrival, DOA)联合估计。
与单基地雷达不同,双基地雷达是根据目标DOD和DOA对信源进行交叉定位,测向模型更加复杂,从而导致谱估计复杂度增加,且会出现三大同步(空间、时间、频率和相位同步)问题[4]。多输入多输出[5](multi input multi output, MIMO)技术的引入,不仅有效解决了双基地雷达三大同步问题,并且提高了目标测向精度和最大估计数,由此双基地MIMO雷达作为研究热点得到进一步发展。2008年,Liu和Chen等提出了基于旋转不变子空间 (estimating signal parameters via rotational invariance techniques, ESPRIT)算法[6,7]的双基地MIMO雷达目标DOD和DOA联合估计方法。2009年,Li和Liu等人采用基于摩尔伪逆矩阵和SVD的ESPRIT算法[8]实现DOD和DOA的自动配对,并且提高了测向精度。2010年,Zhang等提出了降维Capon[9]和多重信号分类(multiple signal classification,MUSIC)算法[10],降低算法复杂度的同时提高了测向精度。2012年,Zheng等提出了一种酉ESPRIT算法[11],利用中心Hermitian矩阵求出信号子空间的实值旋转不变性方程来估计目标DOD和DOA。2013年,Wang等利用改进传播算子算法[12]精确估计目标DOD和DOA,在保证精度的同时极大减小了算法复杂度。2014年,Zheng等利用离散傅里叶变换矩阵还原范德蒙结构[13],以求根MUSIC算法估计目标DOD和DOA,并实现自动配对,有效降低了算法复杂度。2017年,Wen等在考虑空间色噪声平稳特性的基础上利用张量变换的协方差差分方法[14-15]来实现更精确的角度估计,并且计算复杂度较其它基于张量的子空间方法有所降低。2020年,Wen和Shi等利用接收信号的噪声协方差矩阵的稀疏结构,设计了一种新的基于双基地MIMO雷达的去噪方法[16],该方法由于不会带来任何虚拟孔径损失从而提升目标估计性能。
利用常规子空间类算法估计相干信源DOD和DOA时,信号和噪声子空间存在相互渗透现象,此时满秩协方差矩阵会发生秩亏,从而无法准确估计相干信源数目。为解决上述问题,学者们提出了两种方法,分别是非降维类和降维类处理算法,前者主要有频域平滑算法[17]、Toeplitz方法[18],后者主要有空间平滑算法[19]和矩阵重构类算法[20],均可有效解决相干目标测向问题。2015年,Hong等人提出了一种空间差分平滑算法[21],通过基于阵列旋转不变式的发射分集非对称空间平滑方式估计目标DOD和DOA,该算法测向效果更好,但相干信源估计数目受到限制。2017年,Shi等人提出一种联合收发阵列的分集平滑算法[22],通过获得更多协方差矩阵用于空间平滑来提升目标DOD和DOA估计精度,但其计算复杂度过高。
当前,双基地MIMO雷达相干目标测向存在很多待解决问题,尤其是双基地米波MIMO雷达低空目标俯仰维测向问题,多径效应严重影响了DOD和DOA估计精度和稳定性。为应对现代战争中复杂空中威胁,开展双基地米波MIMO雷达低空目标俯仰维测向研究具有重大意义。为此,本文基于双基地米波MIMO雷达抗干扰、反隐身目标和抗击反辐射武器的天然优势,以提升低空目标俯仰维测向性能为出发点,结合经典超分辨测向算法,进一步开展高精度和高分辨率的非相干多目标测向研究。
1 信号模型
如图1所示,考虑一个双基地米波MIMO雷达系统,发射和接收天线为均匀线阵且垂直放置,阵元数分别为M和N个,天线高度分别为ht和hr,阵元间距dt=dr=0.5λ,λ为信号波长。这里假设反射面为光滑平坦地面。
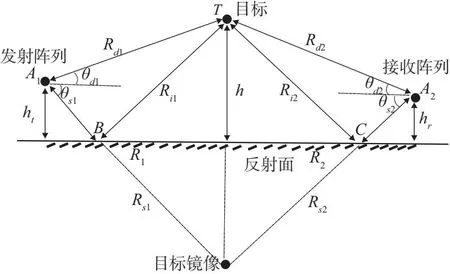
图1 双基地米波MIMO雷达镜面反射信号模型
米波MIMO雷达需考虑发射多径,则经空气传播到达目标处的发射信号为:
x(t)=[at(θd1)+ρ1e-jk0ΔR1at(θs1)]Tφ(t)
(1)
式中:k0=2π/λ;ρ1为发射地面反射系数;θd1和θs1分别表示发射直达波和反射波入射角。观察图1不难发现,发射直达波与反射波波程差ΔR1≈2htsinθd1。at(θd1)和at(θs1)为发射导向矢量,其表达式为:
at(θd1)=[1,e-j2πdtsinθd1/λ,…,e-j2π(M-1)dtsinθd1/λ]T
(2)
at(θs1)=[1,e-j2πdtsinθs1/λ,…,e-j2π(M-1)dtsinθs1/λ]T
(3)
考虑接收多径,则第n个阵元的接收信号为:
zn(t,τ)=[ar,n(θd2)+ρ2e-jk0ΔR2ar,n(θs2)]·
β(τ)x(t)+vn(t,τ)
(4)
式中:β(τ)=αej2πfdτ为不同脉冲下目标复反射系数;fd为多普勒频率;ρ2为接收地面反射系数;θd2和θs2分别表示接收直达波和反射波入射角,接收直达波与反射波波程差ΔR2≈2hrsinθd2。
则整个阵列接收信号为:
z(t,τ)=[ar(θd2)+ρ2e-jk0ΔR2ar(θs2)]β(τ)·
[at(θd1)+ρ1e-jk0ΔR1at(θs1)]Tφ(t)+v(t,τ)
(5)
式中:ar(θd)和ar(θs)为接收导向矢量,表达式为:
ar(θd2)=[1,e-j2πdrsinθd2/λ,…,e-j2π(N-1)drsinθd2/λ]T
(6)
ar(θs2)=[1,e-j2πdrsinθs2/λ,…,e-j2π(N-1)drsinθs2/λ]T
(7)
MIMO雷达发射信号φ(t)满足下式:
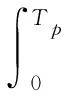
(8)
式中:Tp为1个脉冲持续时间。
利用发射信号对式(5)匹配滤波后可得:
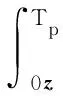
[ar(θd2)+γ2ar(θs2)]β(τ)·
[at(θd1)+γ1at(θs1)]T+V(τ)
(9)
这里,γ1=ρ1e-jk0ΔR1,γ2=ρ2e-jk0ΔR2。
对Z矢量化操作得:
Y=vec(Z)=[at(θd1)+γ1at(θs1)]⊗
[ar(θd2)+γ2ar(θs2)]β(τ)+vec[V(τ)]=Aβ(τ)+V
(10)
式中:vec代表矢量化操作;⊗代表kron积;V为经匹配滤波和矢量化操作后的噪声,若原始噪声为高斯白噪声,则V仍为高斯白噪声,A为复合导向矢量,其表达式如下:
A=[at(θd1)+γ1at(θs1)]⊗[ar(θd2)+γ2ar(θs2)]
(11)
为方便讨论,上述为单目标模型,且只有一条反射路径。对于非相干多目标,其回波信号是单目标回波的叠加,这里不再赘述,直接给出结论。
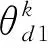
则矢量化后的回波信号矩阵表达式为:
Y=At⊙ArΨ+V=AΨ+V
(12)
式中:⊙为Khatri-Rao 积;Ψ=[β1,β2,…,βK]为目标复反射系数矩阵;复合导向矢量A表达式为:
A=At⊙Ar=At(θd,θs)⊙Ar(θd,θs)=
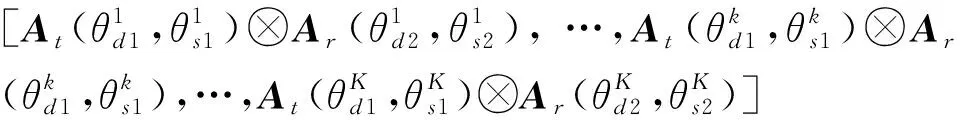
(13)
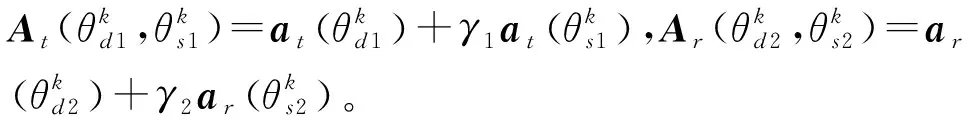
2 DOD和DOA估计
双基地米波MIMO雷达与单基地一样,回波信号矩阵中同样包含多径反射波,即收发导向矢量存在耦合问题,这致使导向矢量与噪声子空间失去正交性。利用空间平滑等解相干算法对仰角估计性能的提升有限,本文提出一种基于新的导向矢量矩阵的广义MUSIC (generalized MUSIC,GMUSIC)和最大似然算法(maximum likelihood,ML)ML算法,该导向矢量矩阵仍与噪声子空间正交。
2.1 基础算法
对式(10)化简变形得:

(14)


(15)
依据最大似然准则,回波数据协方差矩阵可从下式得到:
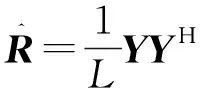
(16)
式中:L为快拍数。
此时广义MUSIC算法谱峰搜索函数为:
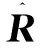
θs1=-arctan(tan(θd1)+2ht/R1)≈-θd1
(18)
θs2=-arctan(tan(θd2)+2hr/R2)≈-θd2
(19)
式中:R1和R2分别为目标在地面垂直投影至发射接收阵列的水平距离。

(20)
则ML算法谱峰搜索函数如下:
式中:trace代表求迹操作。
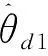
2.2 实值处理算法
为降低算法复杂度,可对回波数据和阵列导向矢量实值处理。定义维度为MN×MN的变换矩阵Π和酉矩阵U如下:
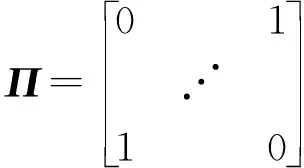
(22)
若MN为奇数,采用式(23),且KM=(MN-1)/2;若MN为偶数,采用式(24),且KM=MN/2。
则经过实值处理的回波数据协方差矩阵和导向矢量表达式如下:
则实值GMUSIC (UGMUSIC)和实值ML(UML)算法谱峰搜索函数如下:
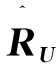
式(27)和式(28)为四维搜索,同理可利用式(18)和式(19)进行降维。
3 算法分析
3.1 算法步骤
步骤 1计算双基地米波MIMO雷达发射、接收直达波和反射波导向矢量;
步骤 2利用式(18)和式(19)进行降维,并根据式(15)计算复合导向矢量,需要降低算法计算量时利用式(26)进行实值处理;
步骤 3对回波信号数据矢量化,然后根据式(16)计算数据协方差矩阵并进行特征值分解得到噪声子空间En;需要降低算法计算量时,利用式(25)对协方差矩阵进行实值处理并进行特征分解得到实值噪声子空间Un;
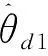
3.2 算法复杂度
本文所提算法复杂度主要包含以下部分:①协方差矩阵构造;②协方差矩阵特征分解;③谱峰搜索。实值处理算法和加法运算增加的计算量很小,在此忽略。此外,1次复数乘法相当于4次实数乘法。则各算法复杂度计算公式如下:
CGMUSIC=4P2L+4P3+4Θ(8P+2P2)
(30)
CML=4P2(L+P)+4Θ(8P+2P2+P3)
(31)
CUGMUSIC=P2L+P3+Θ(8P+2P2)
(32)
CUML=P2(L+M)+Θ(8P+2P2+P3)
(33)
式中:Θ为谱峰搜索次数;P=MN为虚拟阵元数。
图2为所提算法复杂度随虚拟阵元数目变化图,不失一般性,这里假设快拍数L=30,目标数为1,谱峰搜索次数Θ=1 000。不难发现,GMUSIC算法较ML算法计算复杂度更低,随着虚拟阵元数增多,实值处理算法可极大地降低计算复杂度。
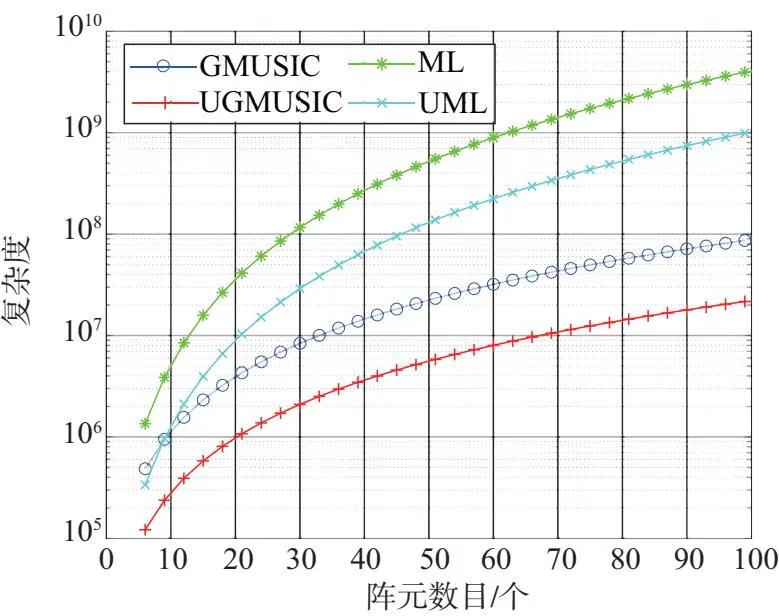
图2 各算法复杂度随虚拟阵元数目变化图
4 仿真实验
假设一个双基地米波MIMO雷达采用垂直放置的均匀线阵作为收发天线,发射接收阵元数分别为M=10和N=8,阵列高度分别为ht=5 m和hr=4 m,阵元间距dt=dr=0.5λ,雷达工作频率为300 MHz。空间低空非相干目标数为K,接收噪声为高斯白噪声,地面平坦光滑,且发射接收地面反射系数分别为ρ1=-0.98和ρ2=-0.95,分别利用GMUSIC、ML、UGMUSIC和UML算法进行DOD和DOA估计,角度搜索范围均为0°~10°,搜索间隔为0.1°。本文采取蒙特卡洛重复实验对比不同算法的测角精度,实验次数为500次,角度均方根误差(root mean square error, RMSE)计算式为:
(34)
(35)
4.1 空间谱对比实验
此组实验条件为信噪比SNR=10 dB,快拍数L=10,低空目标数K=1,DOD和DOA角度分别为θd1=6°,θd2=5°。图3为各算法空间谱,谱峰所在位置为目标DOD和DOA估计值。仿真结果表明,各算法都能准确估计目标DOD和DOA,实值处理算法与基础算法角度估计性能相近,GMUSIC算法谱峰较ML算法尖锐。
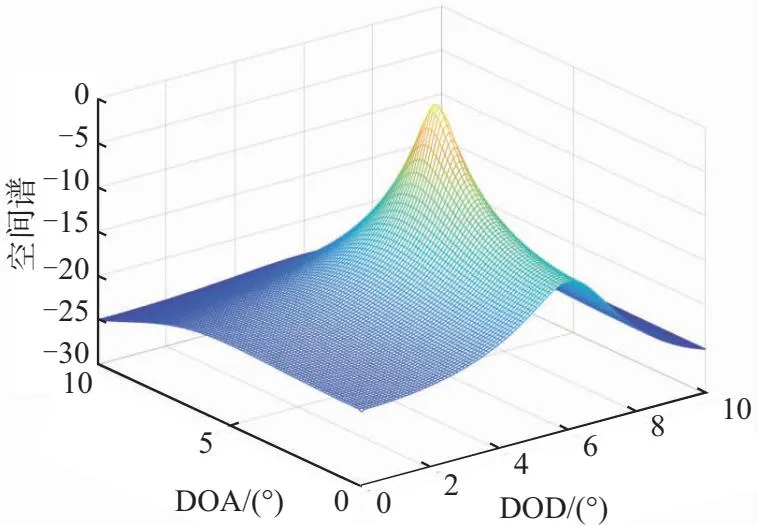
(a) GMUSIC算法
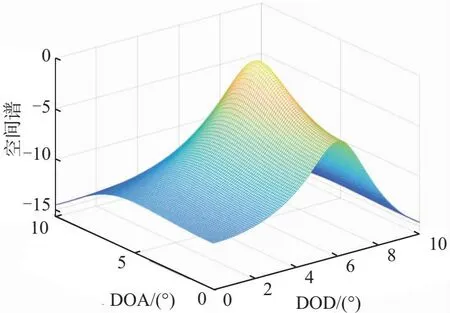
b) ML算法
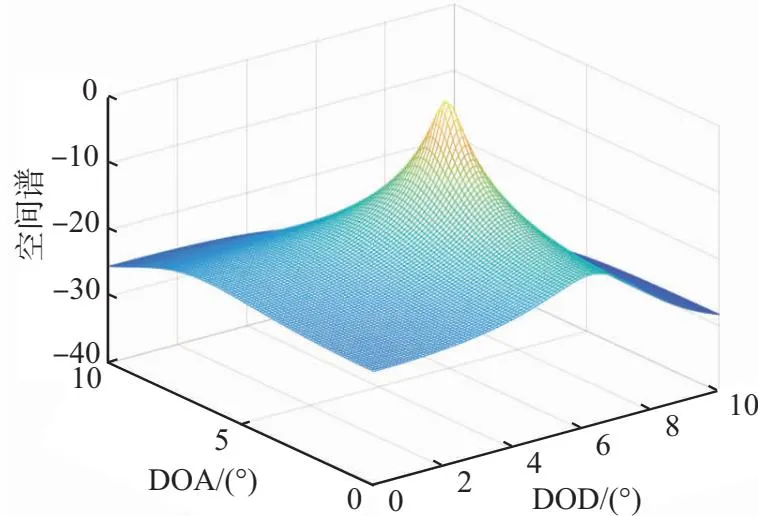
(c) UGMUSIC算法

(d)UML算法
4.2 角度分辨力对比实验
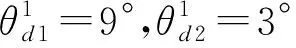
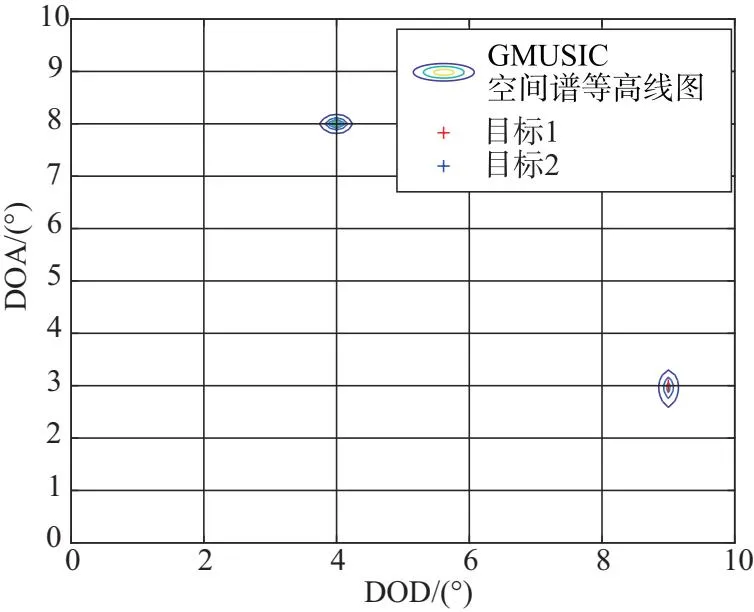
(a) GMUSIC算法

(c) UGMUSIC算法
4.3 信噪比影响测角精度实验
此组实验条件为低空目标数K=1,DOD和DOA角度分别为θd1=6°,θd2=5°,快拍数L=10,信噪比SNR取值范围为-10~10 dB,间隔5 dB,各算法角度RMSE与SNR关系如图5所示。仿真结果表明:在同等信噪比下,GMUSIC算法与ML算法测角精度相近,而实值处理算法测角精度总体上比基础算法低,主要原因是实值处理丢失了回波数据协方差矩阵虚部信息。
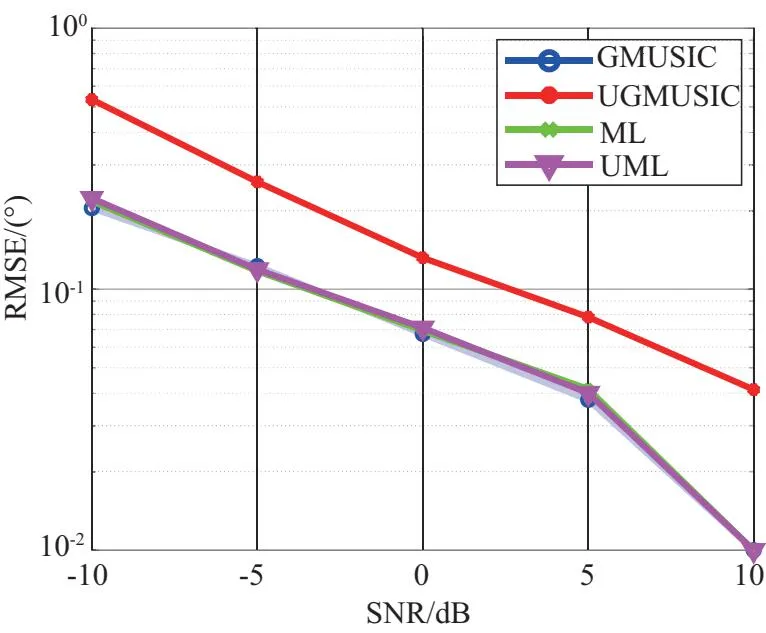
(a) DOD
4.4 快拍数影响测角精度实验
此组实验条件为低空目标数K=1,DOD和DOA角度分别为θd1=6°,θd2=5°,信噪比SNR=0 dB,快拍数L取值范围为10~50次,间隔10次,各算法角度RMSE与快拍数关系如图6所示。仿真结果表明:在同等快拍数下,GMUSIC算法与ML算法测角精度相近,而实值处理算法测角精度总体上比基础算法低,主要原因是实值处理丢失了回波数据协方差矩阵虚部信息。

(a) DOD
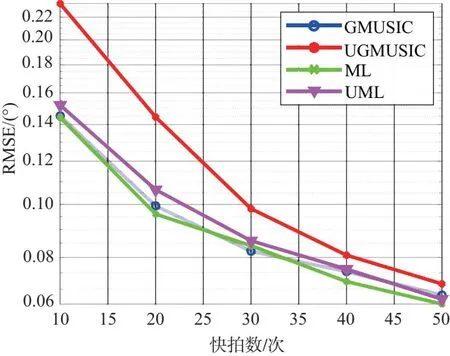
(b) DOA
4.5 幅相误差影响测角精度实验
此组实验条件为低空目标数K=1,DOD和DOA角度分别为θd1=6°,θd2=5°,快拍数L=10,信噪比SNR=0 dB,幅相误差均服从均匀分布,幅度误差变化范围为10%~50%,间隔10%,相位误差变化范围为5°~45°,间隔10°。图7为各算法角度RMSE与幅相误差关系图。仿真结果表明:在同等幅相误差条件下,各算法测角精度总体排序为ML≈UML≈GMUSIC>UGMUSIC,实值处理算法是在牺牲估计精度的前提下降低了计算复杂度。
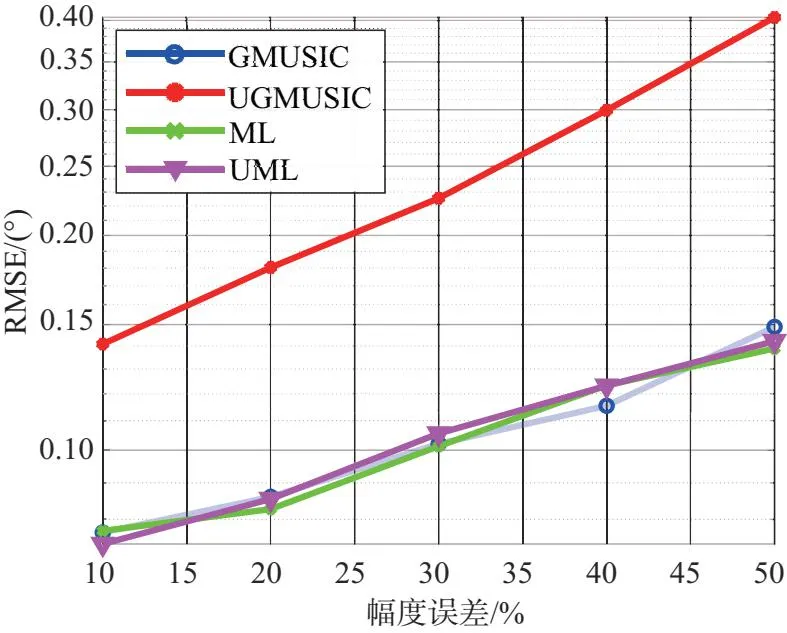
(a)DOD RMSE随幅度误差变化情况
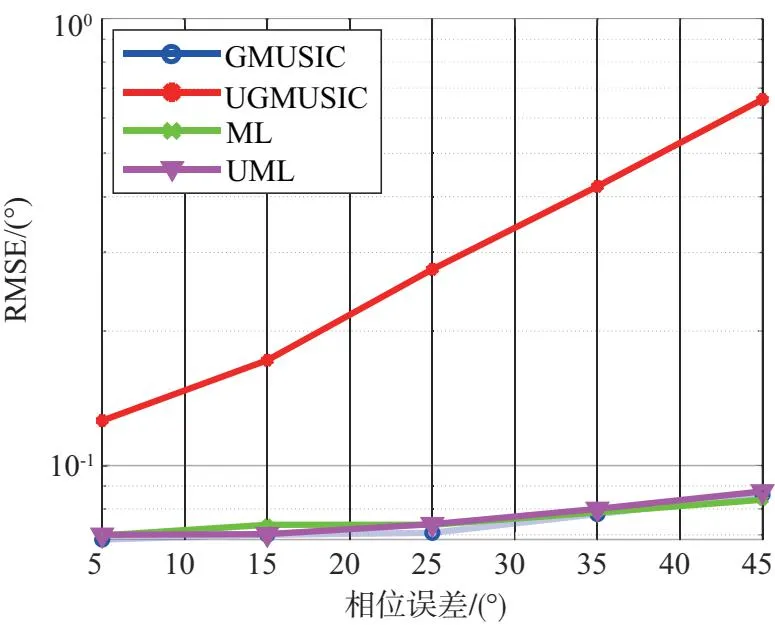
(b)DOD RMSE随相位误差变化情况
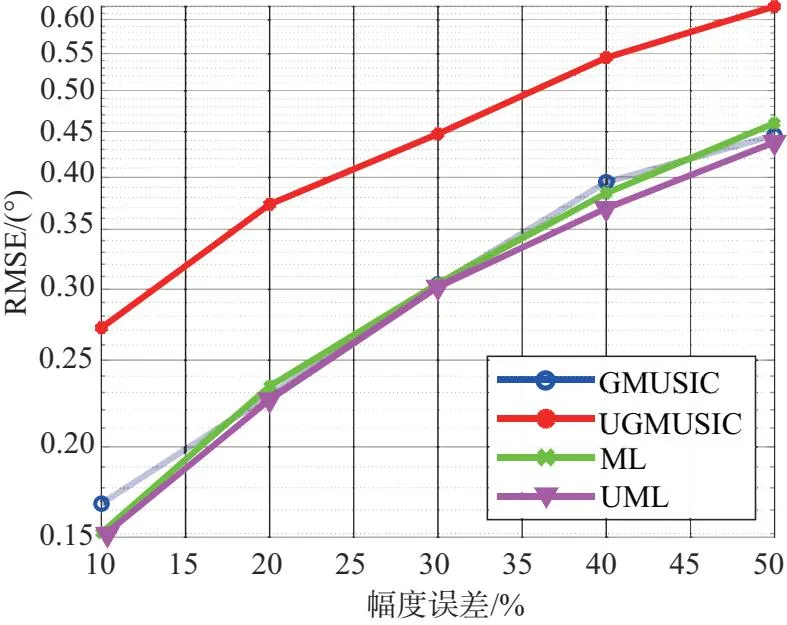
(c)DOA RMSE随幅度误差变化情况
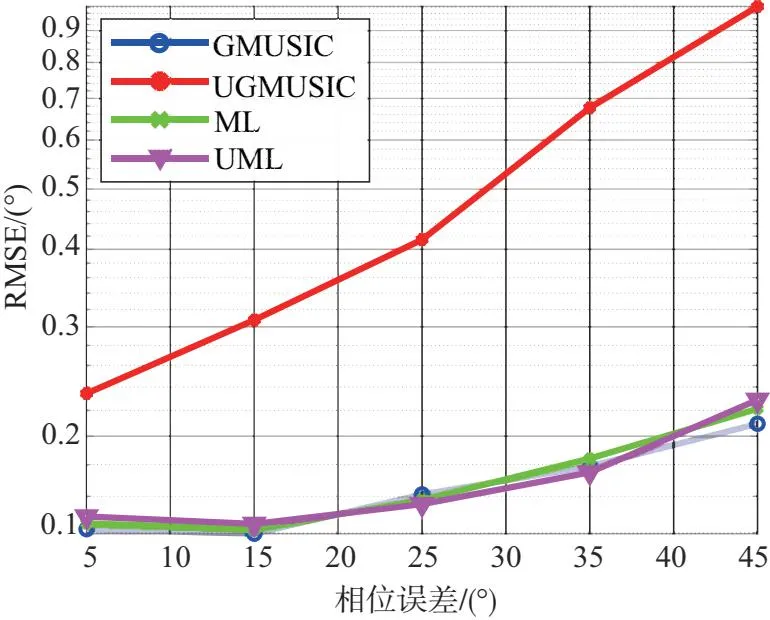
(d)DOA RMSE随相位误差变化情况
5 结语
对于双基地米波MIMO雷达低空目标俯仰维DOD和DOA联合估计问题,本文建立了适用于该场景的镜面反射信号模型,找到了一种新的仍与噪声子空间正交的导向矢量,并结合GMUSIC和ML算法提出了多个非相干目标俯仰维DOD和DOA联合估计方法。实验结果表明:本文所提算法较好解决了多径效应下双基地米波MIMO雷达多个非相干低空信源的俯仰维DOD和DOA估计问题,实值处理算法在损失测角精度前提下降低了运算复杂度,可根据需求选择相应算法。本文信号模型是在理想镜面反射条件下建立的,而实际阵地是复杂的,且电磁环境中充满大量相干信号,对于复杂阵地条件下双基地米波MIMO雷达多个低空相干目标的DOD和DOA估计问题将是下一步研究重点。

