突破函数零点问题区间端点赋值的一种思维策略*
白志峰 张 力 王 辉
⦿ 北京市通州区潞河中学 ⦿ 北京市通州区教师研修中心
函数的零点问题涉及的知识面广、综合性强,解决问题时常常需要把问题转化为探求某个单调区间上存在异号的函数值,结合函数的单调性进一步说明该区间上零点的唯一性.但是,面对灵活多变的函数关系,如何合理赋值,是一个难点.对于含参数的问题,往往更加复杂.有些试题的答案给出的方法取值巧妙,构思灵活,似有突如其来之感,实际解答时很难想到.极限分析法又似乎缺乏理论依据.正所谓“横看成岭侧成峰,远近高低各不同”.本文中通过实例,探析突破解决这一难点的一种易于操作的思维策略——合理放缩,探析零点存在的充分条件.
1 典例分析
例已知函数f(x)=ae2x+(a-2)ex-x有两个零点,求a的取值范围.
解析:求导,可得f′(x)=2ae2x+(a-2)ex-1=(aex-1)(2ex+1).
(1)当a≤0时,f′(x)=(aex-1)(2ex+1)<0恒成立,故函数f(x)递调递减,最多一个零点.

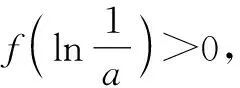


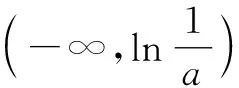
因为ae2x>0,所以
f(x)=ae2x+(a-2)ex-x>(a-2)ex-x.
又因为0 f(x)>(a-2)ex>a-2-x. 到此,证明了x0的存在性,无需再取特值验证.事实上,鉴于以上思路,取x0=a-2,a-3,a-4,……,均可,例如f(a-3)>a-2-(a-3)=1>0. 证法二:f(x)=ae2x+aex-2ex-x>-2ex-x,只需存在x0<0,使f(x0)>0. 鉴于以上思路,取x0=-3,-4,……,均可. 证法一:因为ex>x,所以 证法二[1]:整理得f(x)=ae2x+(a-2)ex-x=ex[aex+(a-2)]-x. 注意到ex>x,所以只需aex+(a-2)≥1. 综上,a的取值范围为(0,1). 本例中我们的目标是寻求函数存在一个正值,在函数具备单调性的条件下,通过加强条件,利用合理缩小,证明了x0的存在性,同时也找到了特值的选取方法.同样地,如果需要证明一个函数存在负值,可以适当放大,放大以后存在负值即可. 本题解题的思维策略是通过合理的放缩进行转化与化归,减少参数的干扰或降低超越函数的复杂程度,拨云见雾,化生为熟,化繁为简,逐步分析、探究零点存在的充分条件.在此,一个简单的不等式链lnx≤x-1 练习1已知函数f(x)=(x-2)ex+a(x-1)2(a>0)有两个零点,求实数a的取值范围. 提示:f(x)在(-∞,1)上是减函数,在(1,+∞)上是增函数. 因为f(1)=-e<0,f(2)=a>0,所以(1,+∞)上f(x)有唯一零点;当x<1时,考虑x<0,ex<1,且x-2<0,所以f(x)=(x-2)ex+a(x-1)2>(x-2)+a(x-1)2=ax2-(2a-1)x+a-2. 练习2已知函数f(x)=xe2x-a,x>0,讨论该函数零点的个数. 提示:f(x)在(0,+∞)上是增函数,f(x)>f(0)=-a. 当a≤0时,f(x)无零点. 当a>0时,f(0)=-a<0,注意到e2x>2x,所以f(x)=xe2x-a>2x2-a. 因为f(0)=b-1≤2a-1<0,注意到ex≥x+1,不妨考虑x>1,可得 f(x)=(x-1)ex-ax2+b≥(x-1)(x+1)-ax2+b=(1-a)x2-1+b.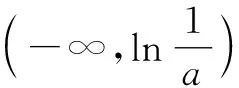
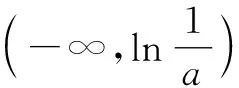
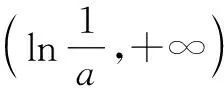


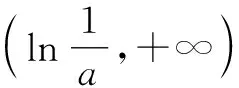
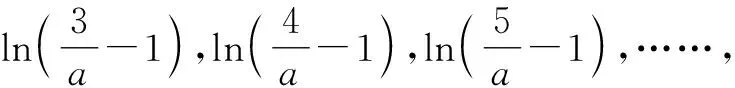


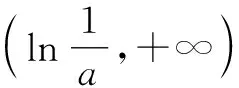
2 思维策略
3 类比练习






