基于覆盖树的自适应均值漂移聚类算法

温柳英，庞 柯

(西南石油大学 计算机科学学院，四川 成都 610500)

0 引 言

经典高效的聚类算法有：K-Means、DBSCAN、Mean Shift(MS)、DPeak等[1-4]。K-Means算法往往只适用于球形数据集或者凸型数据集[5，6]。DBSCAN和DPeak算法通过计算数据的密度，可以识别具有任意形状的数据集，一般情况下密度较高的区域数据质量较高，而密度较低的区域数据更有可能是噪声点。然后现实世界中的数据往往既是非球形，同时也含有噪声，给聚类算法带来了巨大的挑战。

研究人员提出了MS的各种优化算法[7-10]。比如文献[11]提出了一种避免更新全部数据集的方法，该方法减少了算法的时间复杂度，但是算法的精度有所下降。文献[12]结合MS过程，提出一种新的提高聚类精度的方法，但是引入了几个需要人工调整的参数。

鉴于此，本文对原始的均值漂移算法进行了优化，提出了一种基于Cover-Tree[13]的自适应均值漂移聚类算法(MSCT)，在计算漂移向量的过程中引入了最近邻的概念，通过样本点在Cover-Tree数据结构中的K个近邻来计算一个新的KnnShift向量。

1 相关算法介绍

1.1 均值漂移算法介绍

均值漂移聚类算法的基本原理是使用迭代的方法遍历数据集中的所有样本点，搜索点将沿着样本点密度增加的方向“漂移”到当前数据集样本局部密度最大的区域。该算法是通过密度函数梯度的非参数估计方法推导获得的，其中非参数估计方法是从数据集出发对样本密度函数的估计。它不需要任何先验知识，在任意形状的数据分布下都有效，其中最常用的是核密度估计方法。

给定一个大小为n的数据集Xi∈Rd，i=1，2，…n。 使用核函数K(x) 的密度估计为

(1)

其中，h是核函数的半径参数(也被称为带宽)。式(1)中的K(x) 核函数被定义为

K(x)=ck(x2)

(2)

其中，c是一个标准常量，式(2)就是均值漂移过程的数学理论依据，密度函数估计f(x) 是每个样本点处的核函数加权求和的结果。

图1表示了一个均值漂移的迭代过程，其中圆点表示数据集中的一个实例，在大小为n的d维数据集Xi∈Rd中，任意选择一个数据点xi进行一次均值漂移过程，直到数据集中所有的数据点都进行过一次完整的均值漂移过程。

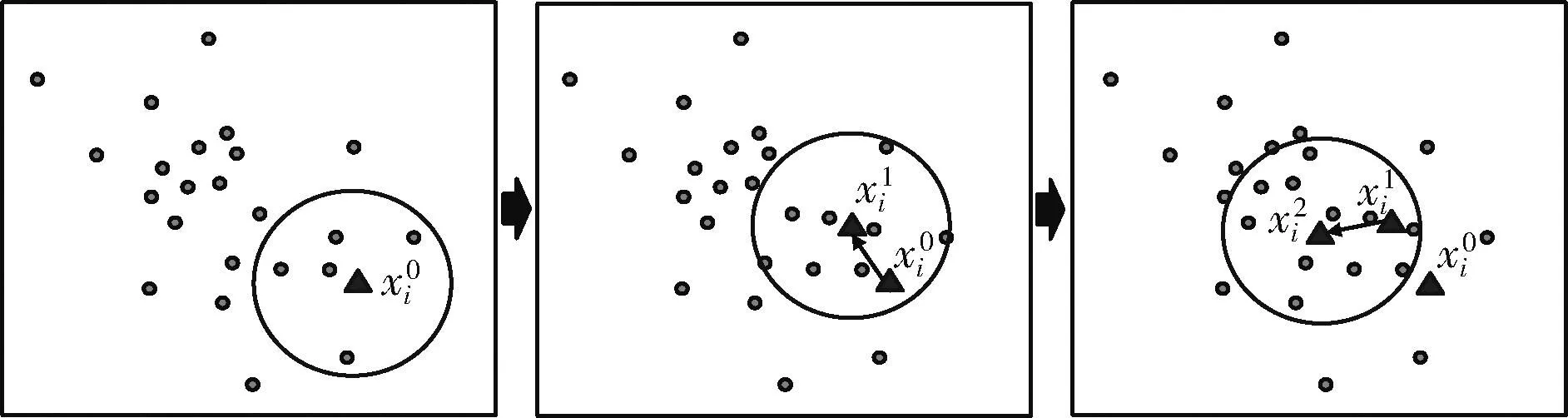
图1 一个均值漂移过程

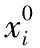
1.2 最近邻算法介绍

作为邻近搜索[14，15]的一种形式，最近邻居搜索是在给定集合中找到最接近给定点的点的优化问题。紧密度通常用不相似函数表示：对象越不相似，函数值就越大。

在最近邻搜索算法中，基于树的各种优化算法不断提出，且被应用于各种密度聚类算法的优化中。比如K-D Tree[16]，虽然K-D Tree非常的有效，但是它只能在低维数据集上有较好的表现。之后人们提出了一种和K-D Tree原理相似的算法——VP Tree。与K-D Tree使用一个超平面来将数据点划分为两个部分相似，VP Tree使用了优势点的概念，通过计算其它点与优势点的距离来将数据点一分为二。之后Alina等提出了一种新的最近邻优化算法Cover-Tree，它可以以O(log(n)) 的时间复杂度完成一次最近邻查找，提高了最近邻算法的效率。

2 基于Cover-Tree的均值漂移聚类算法

2.1 MSCT原理

原始的MS算法聚类效果十分依赖于带宽参数的主观选取，在处理分布不均匀，密度变化大的数据集时，算法的聚类结果不够精确。在原始算法计算均值漂移向量的过程中，会计算一个数据点在某个带宽范围内所有的点。这样一个计算过程可以被转换为Knn问题。

本文将最近邻的概念引入到了MS算法局部密度的计算过程中，获得密度梯度估计公式如式(3)所示

(3)

式(1)中核函数K(x) 会先计算出点x带宽范围h内所有的点，之后计算出这些点的重心。对于数据集中所有的xi来说，在数据集不同的密度范围内，这个带宽范围h是一个固定的值，无法自适应数据集不同密度区域。

式(3)中核函数K(x) 的带宽参数被替换为最近邻问题中的k，根据样本点x在Cover-Tree数据集中的k个近邻来计算每一步的漂移向量，记此时的漂移向量为Knn-Shift。此方法在不同数据集以及不同数据密度上都能自适应的产生一个带宽范围h。

f(x) 被定义为点x具有核函数K(x) 的多元核密度估计，此时结合核函数式(2)可获得式(4)计算结果

(4)

式中的第二部分，即为Knn-Shift如式(5)所示

(5)

给定一个点xi，其第t次迭代过程可以由如下公式表示

(6)

图2展示了通过最近邻k获得Knn-Shift向量的一个示意图，此时k=3。MSCT算法首先会使用输入的数据构建一个Cover-Tree数据集，之后会通过输入的参数k计算每一个样本点的Knn-Shift。

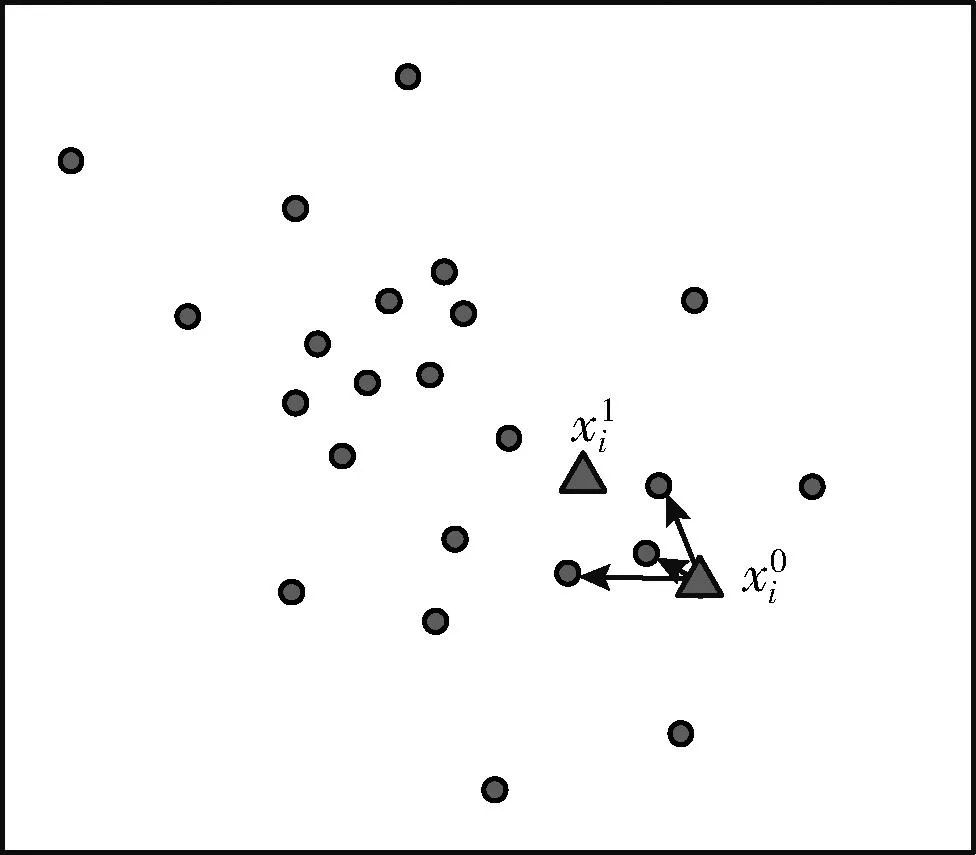
图2 Knn-Shift 漂移过程

2.2 Cover-Tree的构建算法

数据集S上的Cover-Tree数据结构是一个有层级结构的树，它的每个层级都是其下方层级的“覆盖”。树的每个层级都有一个下标i，该下标随着树层级的下降而减小。

令Ci表示数据集S中与Cover-Tree第i层节点相关的点集，我们有如下定义：

定义1 嵌套：Ci⊂Ci-1

即一旦点p∈S出现在Ci中，那么树中的每个比i低的层级都有一个与p关联的节点。

定义2 覆盖：∀p∈Ci-1，∃q∈Ci。

使得d(p，q)<2i， 且q是p的父节点。其中d(p，q) 表示两点之间的距离。

定义3 分隔：∀p，q∈Ci， 有d(p，q)<2i。

算法1的Cover-Tree构建算法是一个递归算法，算法中的第一步会创建一个空的Cover-Tree数据结构Q，Qi是第i层所有点的集合。之后的步骤会对数据集S中的每一个样本点p进行插入操作，每一次的插入操作都从Q的根节点开始，并根据定义2对距离的定义来进行插入，将数据集S中的所有点进行插入操作后获得一个Cover-Tree数据集Q。

算法1: BuildCoverTree

输入: 数据集S, Cover-TreeQi, 层级i

输出: Cover-Tree数据集Q

(2)Ifd(p,q)<2i then

(4)IfBuildCoverTree(p,Qi-1,i-1)=null&&d(p,Qi)≤2ithen

(5) 选择q∈Q且满足d(p,q)≤2i的p

(6) 将p插入children(q)中

(7)EndIf

(8)else

(9) returnnull

(10)else

(11) returnnull

(12)EndIf

2.3 MSCT算法

图3展示了MSCT算法的框架，对于任意一个数据集，MSCT首先会使用算法1来构建一个Cover-Tree数据集，之后在MeanShift过程中结合该数据集和输入的参数k计算出一个新的Knn-Shift量，通过Knn-Shift的值来判断一个样本点的漂移过程是否结束。当数据集所有样本点完成漂移过程后，按照MeanShift算法的分配策略进行最终的举例，获得聚类结果。

图3 MSCT算法框架

MSCT算法的具体步骤如算法2所示。

算法2: MSCT算法

输入: 数据集S, 近邻k

输出: 聚类结果C

(1)Q=BuildCoverTree(S,Qi,i)//算法1

(2)Forxq∈Sdo

(3)KnnShift=∞ //初始化漂移向量

(4)FSOld=∅,FSNew=∅//初始化频率数组

(5)While(KnnShift≠0)

(6)M=FindNearrest(Q,xq,k)

(7) 集合M中的点FxM访问频率加1

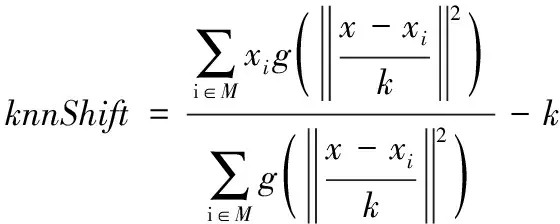
(9)xq=xq+KnnShift

(10)Endwhile

(11)IfC=∅then

(12)C.Add(cq)

(13)else

(14)IfFSOld>FSNewthen

(15)xq∈COld

(16)else

(17)xq∈CNew

(18)C.Add(cNew)

(19)endif

(20)endif

(21)endfor

在MSCT算法中，第(1)行首先通过算法1构建一个Cover-Tree数据集。第(2)行对数据集S中的每一个样本点进行一次Knn-Shift操作。第(3)、第(4)行为初始化过程，记此时的Knn-Shift向量为一个极大值，数据集S中的每一个样本点都有两个名为频率计数标志的量，分别记为FSOld、FSNew。第(5)行通过Knn-Shift量的值来控制漂移过程的结束。第(6)行为在Cover-Tree数据集Q中找到当前样本点xq的k个最近邻，记为集合M。第(7)行将集合M中的元素频率计数标志量加1。第(8)行通过获得的集合M使用式(5)来计算一个新的Knn-Shift量。第(9)行使用新的Knn-Shift计算下一个虚拟的样本点xq。第(11)～第(20)行执行MeanShift算法最后的聚类分配策略，按照漂移过程中不断更新的频率计数标志来划分最终的聚类。

2.4 复杂度分析

MSCT算法的主要过程分为两个部分，首先第一部分为通过输入的数据集创建并初始化一个Cover-Tree数据结构即算法1，这个过程的空间复杂度为数据集的维度O(n)， 时间复杂度为O(nlog(n))。 第二部分为算法2的第(2)行至第(21)行，这个部分为对数据集的每一个点进行一次Knn-Shift操作，总的时间复杂度为O(tnlog(n))，t为一次Knn-Shift过程中的迭代次数。所以MSCT算法总的时间复杂度为O(nlog(n)+tnlog(n))=O(tnlog(n))， 空间复杂度为O(n)。

3 实验结果与分析

为了验证实验算法的有效性，本文采用了一系列的数据集进行详细的对比实验，数据集使用了聚类算法评测时常用的一些数据集，其中包括UCI(University of California Irvine)数据集和人工数据集。

实验对比部分，我们选取了几种常见的聚类算法作为对比，分别为MeanShift、DBScan、K-means。评价指标选择调整互信息(adjusted mutual information，AMI)、调整兰德系数(adjusted rand index，ARI)、FMI指数(Fowlkes-Mallows index，FMI)。它们的取值范围分别为：AMI∈[0，1]、 ARI∈[-1，1]、 FMI∈[0，1]。 在之后的表格实验数据中，这3种指标的值越大，就表明该算法越有效，算法效果越好，它们的取值范围为-1到1之间的浮点数。

实验中使用到的数据集如表1和表2所示。本次实验使用Java编程实现，Windows10操作系统，硬件配置为Inter Core i7-9700k CPU @ 3.60 GHz，16 GB RAM， RTX2080S显卡。

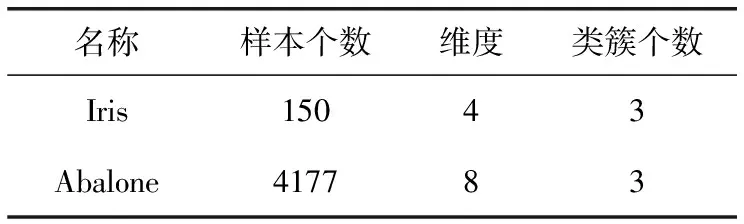
表1 UCI数据集信息

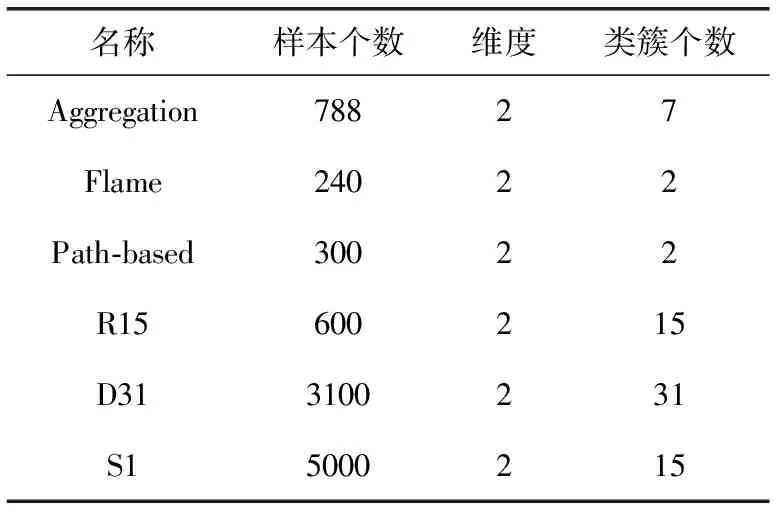
表2 人工数据集信息

本文中使用了6个人工数据集，以及2个UCI数据集进行了仿真实验，数据集的基本信息见表1、表2。

由表中数据可知，选取的数据集包含了不同的数据维度和数据数量。

表3给出了MSCT算法与标准的MS算法以及DBScan，K-means算法的详细实验对比，表中的各评价指标值均保留结果小数点后三位，表格中的数字加粗值表示当前算法相比其它对比算法有较好的聚类结果，其中MSCT的输入参数为最近邻的个数K(整数)，MS算法的输入参数为带宽参数(浮点数)，参数输入设置参考了文献[5]。

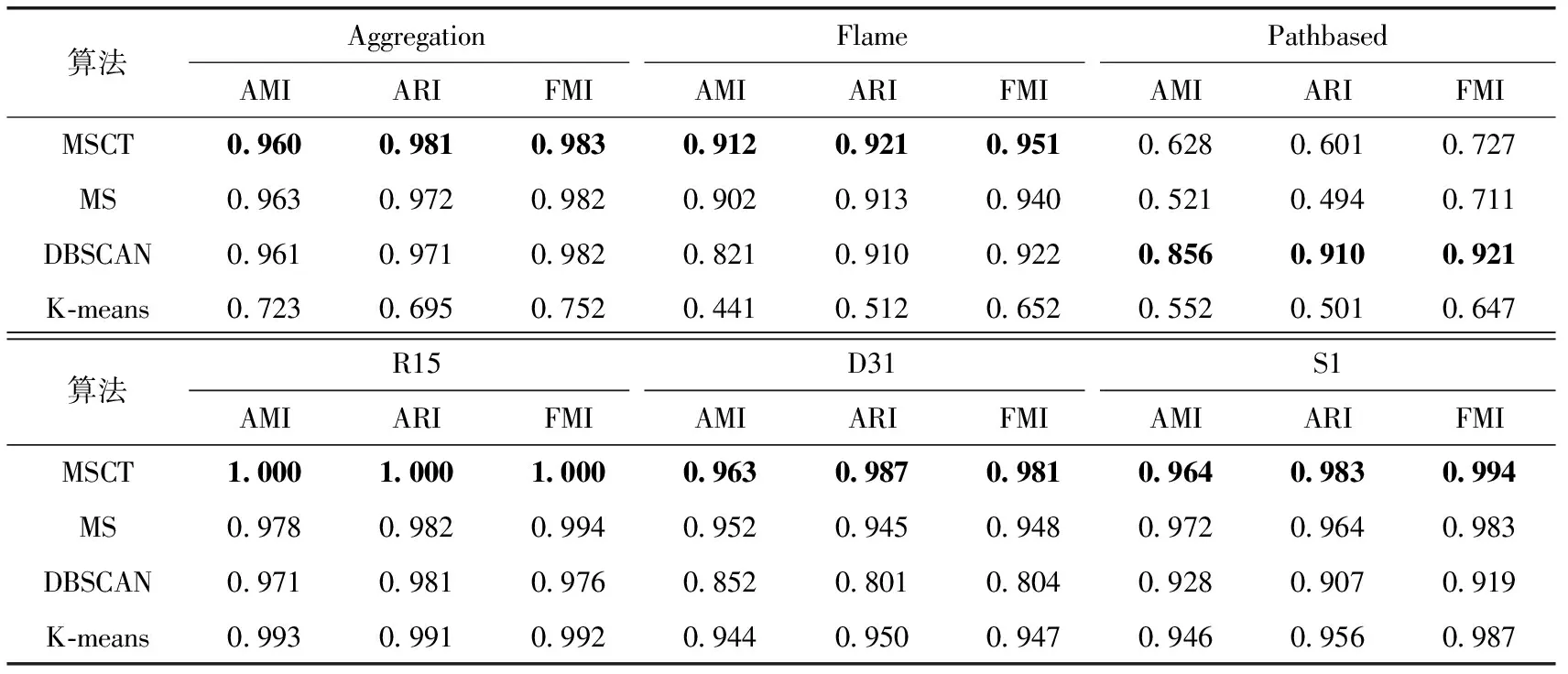
表3 各聚类算法评价指标

表3中的数据都是人工数据集的实验结果。从表中可以看出，在AMI、ARI、FMI评价指标上，自适应MSCT算法在Aggregation、Flame、R15、D31、S1数据集上获得了最优的聚类效果，自适应MSCT算法是在原始MS算法上进行改进获得的结果。

图4图5是Iris数据集和Abalone数据集分别使用DBSCAN、MS、MSCT算法进行实验获得的结果。

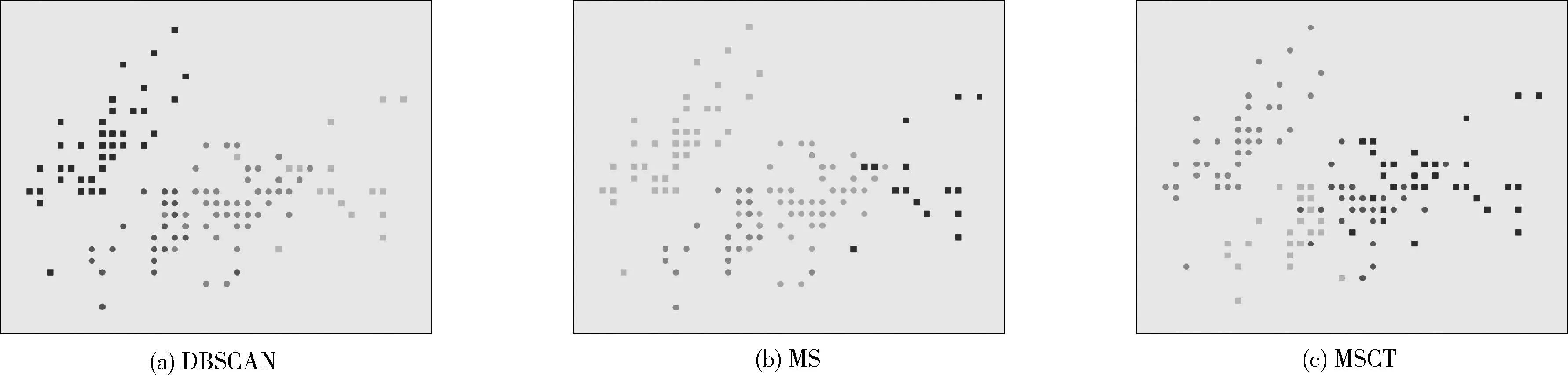
图4 Iris数据集聚类效果

图5 Abalone数据集聚类效果

这两个数据集都选自于UCI数据集，其中Iris数据集有150个样本数据，3个类簇，除了一个密度较大的类簇以外，其余两个类簇的样本点的分布较为接近且分散，数据集的密度分布不均匀。由图4可以看出，DBSCAN算法在这一数据集上获得了4个类簇，图上的4个方框区域，原算法MS和改进的算法MSCT获得的结果总体是相似的，都得到了3个聚类的正确结果，但是在中心密度较大的区域，一部分数据样本上，MSCT算法获得了更好的聚类结果，而DBSCAN算法在聚类过程中获得了不太精确的聚类结果。图5的Abalone数据集有4177个样本数据，8个属性，3个簇类，这一数据集数据样本维度较多，数据分布复杂，由图5可以看出，在这一数据集上DBSCAN算法聚类效果不太理想，而原始的MS算法在聚类过程中在数据密度分布变化较明显的区域(图5上方的区域)获得了错误的类簇个数，MSCT算法得到的聚类结果明显好于MS算法。

图6是R15数据集，该数据将有600个样本数据，15个类簇，数据集分布分为外围的低密度区域，以及中心的高密度区域两个部分。能看到3种算法都获得了比较好的结果，这是因为作为一种密度聚类算法，该数据集在不同的密度区间上的划分有明显区别，3种算法都能在该种类型数据集上获得很好的聚类结果。

图6 R15数据集聚类效果

从表3以及图6至图8的数据中可以看出，在大多数人工数据集上，自适应MSCT算法相较于其它对比算法在3个评价指标上都获得得更好的结果，MSCT算法提出的针对数据集分布不均匀，密度变化大的Knn-shift方法，能够很好解决带宽参数选取敏感的问题，解决人为参与实验时的主观性问题。在表3中我们发现。MSCT算法在Pathbased数据集上的表现不如其它对比算法表现好，通过分析数据集发现，该数据集的数据分布与其它实验数据集有很大区别，MSCT算法在聚类过程中正确的获得了聚类个数，但是在分配过程中，由于其中一个聚类的分布区域过大，将这一聚类中的某些数据点进行了错误的分类。

对MSCT算法在这一类数据集出现的问题进行了分析，主要原因如下：

(1)对于某些数据集来说(如实验中的Pathbased数据集)，不同类之间的密度差异较小，且类中的数据点分布较为接近，这对于MSCT算法来说有较高难度进行正确划分。

(2)MSCT算法在对所有数据集进行Knn-shift之后的合并过程中，优先选取了类间距离最近的类簇进行了合并，在Pathbased这类数据集上，这种合并方法并不是最优的。

针对以上发现的问题，之后的研究会在现有基础上改进类簇的合并过程，在合并过程中考虑多种因素的影响，如簇内相似性、簇间相似性等等，来优化合并过程。

图7和图8是Aggregation，S1数据集的聚类结果图，由图中可以看出，两种数据集不同密度区域的样本点有比较接近的一部分，3种对比算法算法主要在每一部分样本点的边缘部分的分类上有不同的聚类结果，从图7个图8中可以看出在某些样本点的聚类结果上，MS算法没有正确获得聚类结果(图7和图8中使用虚线方框标记的部分样本点)，再结合表3中的有效性评价指标AMI、ARI、FMI的值，可以得到结论MSCT算法在大多数密度变化较大的数据集上获得了比原算法更优的聚类结果，聚类效果更好。

图7 Aggregation数据集聚类效果

图8 S1数据集聚类效果

4 结束语

本文中将Cover-Tree算法应用到了原始的MeanShift算法中，得到了新的MSCT算法，解决了带宽参数对聚类结果的影响，实验结果表明能获得更加精确的聚类结果，MSCT算法适用于处理样本密度变化大的数据集，在这些数据集上有比原始算法更好的表现。

实验过程中也发现一些可以进一步优化的问题，本文主要是针对漂移过程进行了改进，之后会尝试对漂移过程之后的类簇合并过程进行优化，以及将MSCT算法应用于实际问题。