基于深度强化学习的复杂网络可扩展社区检测
马玉磊,钟潇柔
(1.新乡学院 继续教育学院,河南 新乡 453000;2.新乡学院 计算机与信息工程学院,河南 新乡 453000)
0 引 言
复杂网络[1]具有无尺度性、高聚类系数以及小世界性的特点,常用于表达现实系统中客体之间的关系,在生物领域的蛋白质网络、无线通信领域的蜂窝网络及计算机领域的社交网络中具有很大的应用价值。社区性是复杂网络的一个重要特性,社区内客体的相似性与关联性较高,社区间客体的相似性与关联性则较低,社区检测[2]是分析复杂网络的一个重要步骤。
传统的社区检测算法主要包括基于启发式与基于模块度两类算法。格文-纽曼算法[3]是一种经典的基于启发式的算法,自Newman提出模块度的概念起,基于模块度的社区检测算法层出不穷,如模糊模块度社区检测算法[4]、局部模块度社区检测算法[5]。大多数基于模块度的社区检测算法核心思想是以网络模块度为目标函数,采用不同的启发式算法对模块度进行优化,提高社区划分的质量,其中蚁群算法[6]、多目标演化算法[7]以及凸优化算法[8]均取得了良好的效果。
近年来,深度学习技术被成功用于复杂网络的社区检测任务。文献[9]利用多层自编码器与森林编码器构成二级级联模型,对相似度矩阵进行降维和表征学习处理,最终使用K-means得到准确的社区划分结果。文献[10]采用基于s跳的方法对网络图的邻接矩阵进行预处理,采用K-means算法对低维特征矩阵进行聚类得到网络社区结构。虽然深度学习具有较强的感知能力,能提取丰富的网络拓扑结构特征,但深度学习缺乏一定的决策能力,导致通过深度学习识别的社区边界准确性不足。考虑强化学习[11]具有较强的自适应决策能力,因此将深度学习与强化学习结合,出现了深度强化学习模型[12]。目前,深度强化学习在交通信号控制[13]、路由策略决策[14]以及功能链迁移[15]等任务上取得了突出的效果,在多个领域中的性能优于基于启发式的学习算法。
受此启发,本文借助深度强化学习为复杂网络的社区检测问题提出新的解决思路。为了在复杂网络社区检测的效率与准确性之间取得平衡,设计了两阶段的社区检测框架。第一阶段基于网络拓扑结构初始化社区结构,第二阶段基于深度强化学习对网络社区结构进行微调与优化,利用深度强化学习强大的感知能力与决策能力提高社区结构的准确性。本文的主要贡献有以下3点:①提出新的相似性度量指标,该指标度量了节点在网络拓扑结构上的相似性;②将深度强化学习模型应用于社区检测问题,采用经验重复机制增强神经网络的收敛稳定性;③提出新的社区局部优化算子,改善社区边界划分的准确性。本文算法的两个阶段均为无监督学习,通过深度强化学习对不同规模与结构特点的网络均能进行较好的感知与决策,因此具有较好的可扩展性。
1 系统框架设计
将复杂网络建模为图,表示为G=(V,E), 其中V与E分别为图的节点集与连接集,社区发现问题可描述为将G化分成若干个子图 {G1,G2,…,Gn}, 子图内节点间的相关性较高,而子图之间节点的相关性较低。
为了加快复杂网络社区检测的效率,本文采用两阶段的社区检测框架,社区检测流程如图1所示。第一阶段基于网络拓扑结构初始化社区结构,该阶段根据邻域度方差检测网络中的候选社区中心,然后基于相似性进行标签传播并建立网络的初始化社区。第二阶段基于深度强化学习对网络社区结构进行微调与优化,利用深度强化学习强大的感知能力与决策能力提高社区结构的准确性。

图1 基于深度强化学习的社区检测流程
2 复杂网络的社区初始化
2.1 候选社区中心估计
为了识别网络中的中心节点,计算每个节点在其邻域内的度数方差,称为邻域方差(neighbor variance,NV)。邻域方差(NV)的计算方法定义为
(1)
输入网络的实例如图2(a)所示,估计的候选社区中心如图2(b)所示。
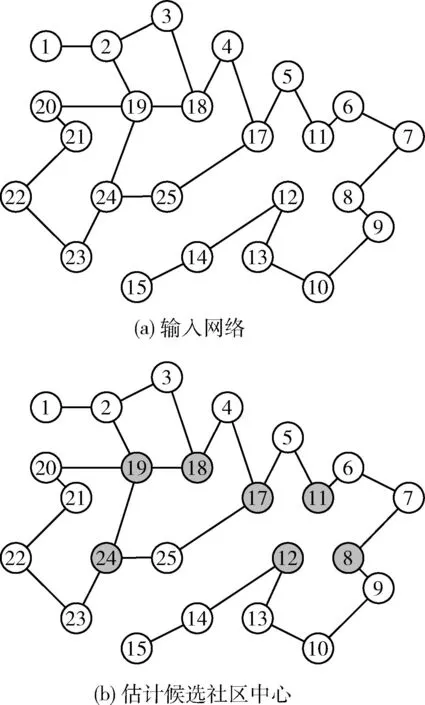
图2 社区中心
候选社区中心估计步骤如下:
步骤1 计算网络G每个节点的NV值保存于向量HV中,将HV的元素按数值降序排列。
步骤2 将第1个节点(HV值最高)作为一个候选社区中心。
步骤3 遍历HV的每个节点,计算当前节点与候选社区中心之间的平均距离,如果两者之间的距离大于网络的平均距离,那么认为当前节点为另一个候选社区中心,否则为普通节点。
平均距离的计算方法如下
(2)
式中:d(u,v) 为节点u与v之间的最短路径,V为网络的节点数量。
2.2 节点相似性评估
2.2.1 网络结构相似性度量
本文提出节点相似性度量方法,该方法在网络拓扑结构上评估节点间的相似性。该度量方法基于两点理由而来:①两个节点的邻域结构越相似,两者的相似性应当越高;②两个节点包含的共同邻居数量越多,两者的相似性应当越高。本文分别提出了邻域结构相似性与共同邻居数量两个度量方法。
(1)邻域结构相似性
首先,计算节点vi与其邻居节点的度数差值,计算方法如下
(3)
式中:vi表示目标节点,δ()函数计算节点的度数,vm为vi的邻居节点,即vm∈N(vi),k为vi的邻居数量,m与i均为节点的索引。
图3(a)所示是网络实例的NSI计算结果,NSI(vi)=|5-4|+|4-4|=1,NSI(vj)=|5-3|+|5-4|+|5-5|=3。
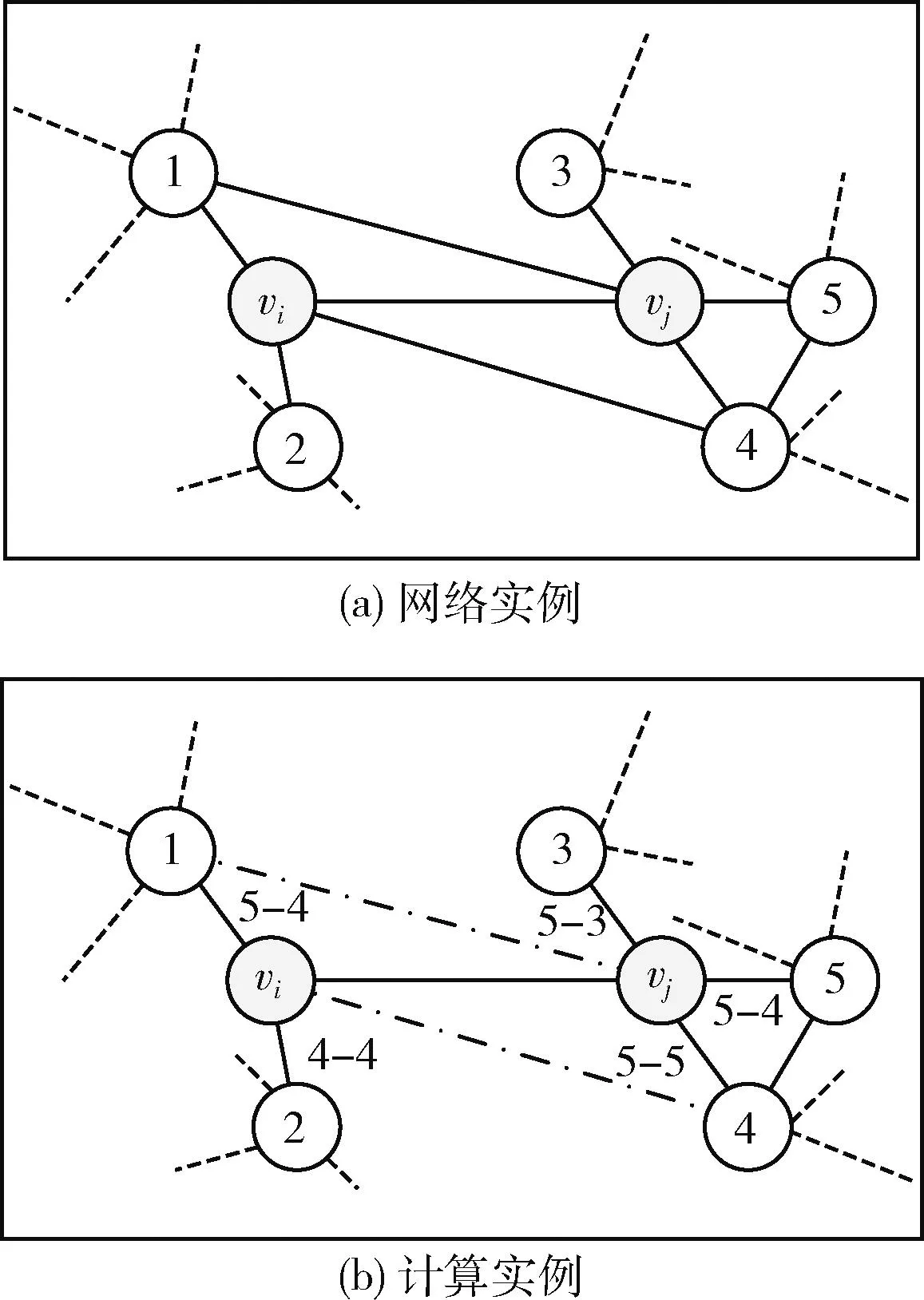
图3 节点相似性度量的实例
然后,计算节点vi与vj之间的度数差值差异,计算方法如下
DNSI(vi,vj)=|NSI(vi)-NSI(vj)|
(4)
式中:vi与vj表示两个节点。
(2)共同邻居数量
共同邻居数量的数学式可表示为
(5)
式中:vp∈N(vi),vq∈N(vj),N(vi) 表示vi的邻居节点。 λ(a,b) 为指示函数:如果a与b为邻居节点,那么λ(a,b)=1, 否则λ(a,b)=0。
图3(a)是网络实例的DNSI(vi,vj)=|1-3|=2, 图3(b)实例中的点化线表示vi与vj的共同邻居连接,即NS(vi,vj)=2。
将邻域结构相似性与共同邻居数量结合,给出两个节点在网络拓扑结构上的相似性度量方法,计算方法如下
(6)
式中:vp为vi的邻居节点,P为vi的邻居节点数量,vq为vj的邻居节点,Q为vj的邻居节点数量。
2.2.2 构建近邻矩阵
搜索网络中各节点的k-近邻集,将节点vi的k-近邻集按相似性降序排列,该处理的数学模型可表示为
DN(vi)=desort(kN(vi))
(7)
式中:kN(vi) 输出节点vi的k-近邻节点集,desort()函数将节点集降序排列。
函数DN()为每个节点产生一个k-近邻列表,基于每个节点的k-近邻列表为网络全部节点创建一个近邻矩阵。一个简单的近邻矩阵如图4所示。
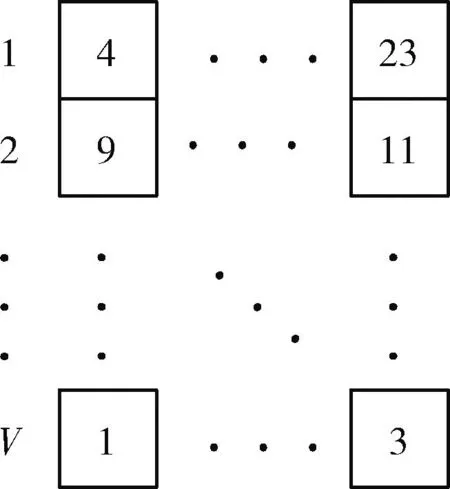
图4 近邻矩阵
2.3 基于标签传播的社区初始化
由候选社区中心开始标签传播过程,每个节点根据近邻矩阵将其标签初始化为最相似邻居的标签,该初始化策略的数学式可表示为
(8)
式中:Li与Lj分别表示节点vi与vj的社区标签,vj是与节点vi最相似的节点,argmax()表示返回最大值。
标签传播处理后的社区划分结果如图5所示。

图5 基于标签传播建立的社区结构
3 基于强化学习的社区优化方法
3.1 社区局部优化
3.1.1 社区局部结构评价指标
模块度是评估复杂网络社区结构的经典指标,广义的模块度计算公式可表示为
(9)
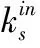
3.1.2 社区局部结构优化算子
社区性是复杂网络的一个重要特性,社区内客体的相似性与关联性较高,社区间客体的相似性与关联性则较低。本文基于社区性的特点提出了新的社区局部结构优化算子:如果当前社区内的某个节点与其它社区存在密集的连接,那么将该节点迁移至其它社区,评估迁移前后网络模块度的增减情况。算法1总结了社区局部结构优化算子的处理过程。
算法1:社区局部优化算子
输入:Trymax,网络G
输出:优化后的社区结构NewModularity,优化后的网络模块度Gmodularity
(1)Foreachtryfrom 1 toTrymax//Trymax与网络结构有关
(2) Community=InitCommunit(); //输入当前社区结构信息(强化学习的状态信号)
(3) Foreach node in Community
(4)SC←CommunityofNode(node);
(5)Nout←节点连接到其它社区的边数;
(6) Endfor
(7)Noutlist←SortDescend(Nout); //按外部连接数降序排列
(8)Nmax←Nout值大于Nth的节点数量; //基于阈值判断外部连接数
(9)InitModularity←当前网络的模块度;
(10)j←1;LModularity←InitModularity;
(11) Foreach iter from 1 toNmax
(12) 将Noutlist[iter]节点迁移到最相似的外部社区; //度量相邻节点间的相似性
(13)NewModularity←计算网络的模块度; //计算迁移后的网络模块度
(14) If (NewModularity>LModularity)
(15)LModularity←NewModularity;//更新局部模块度
(16) 更新社区结构; //强化学习的状态信号
(17) End if
(18) Endfor
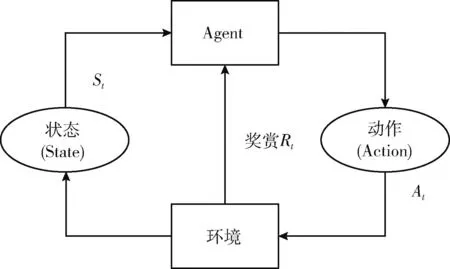
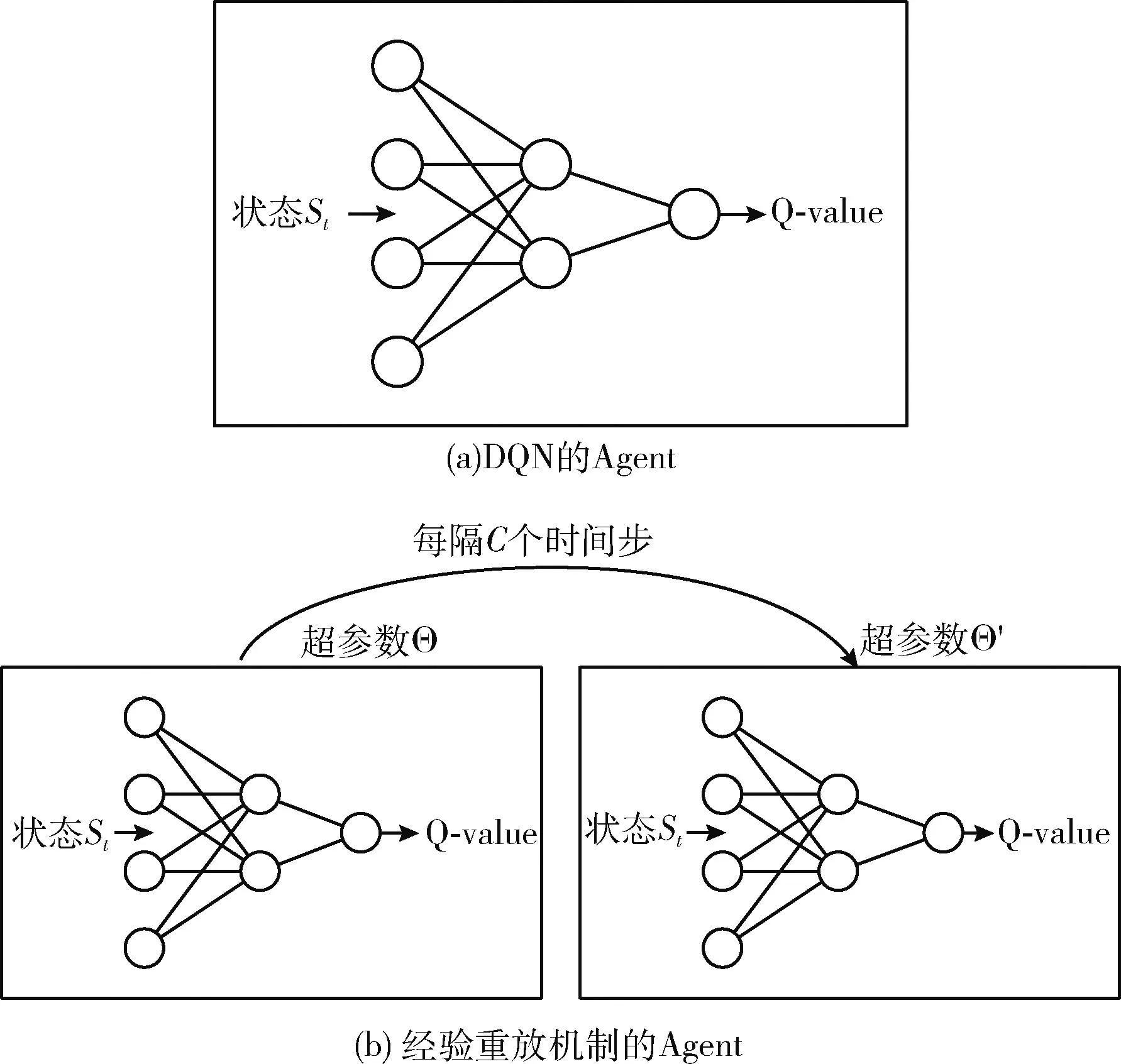
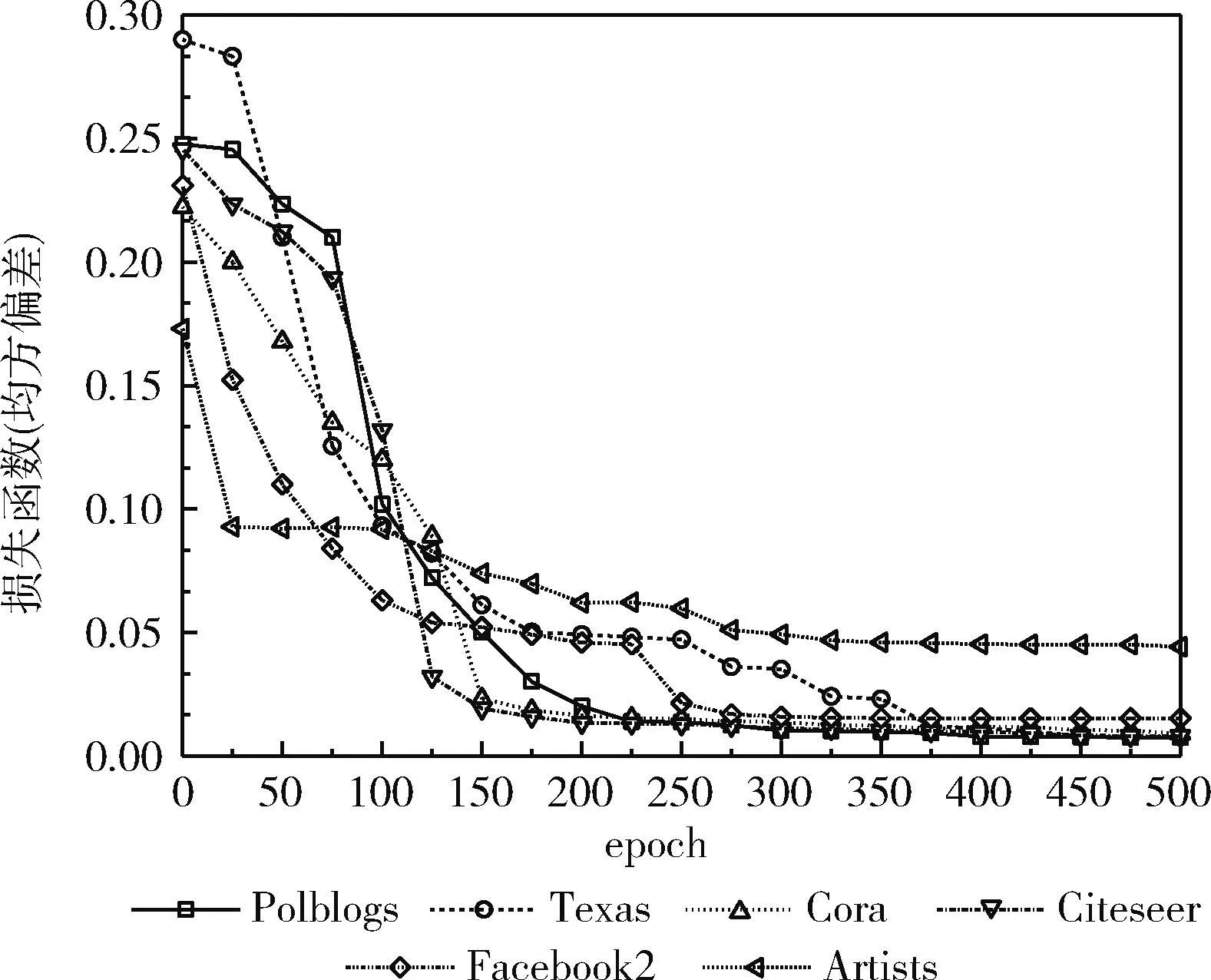
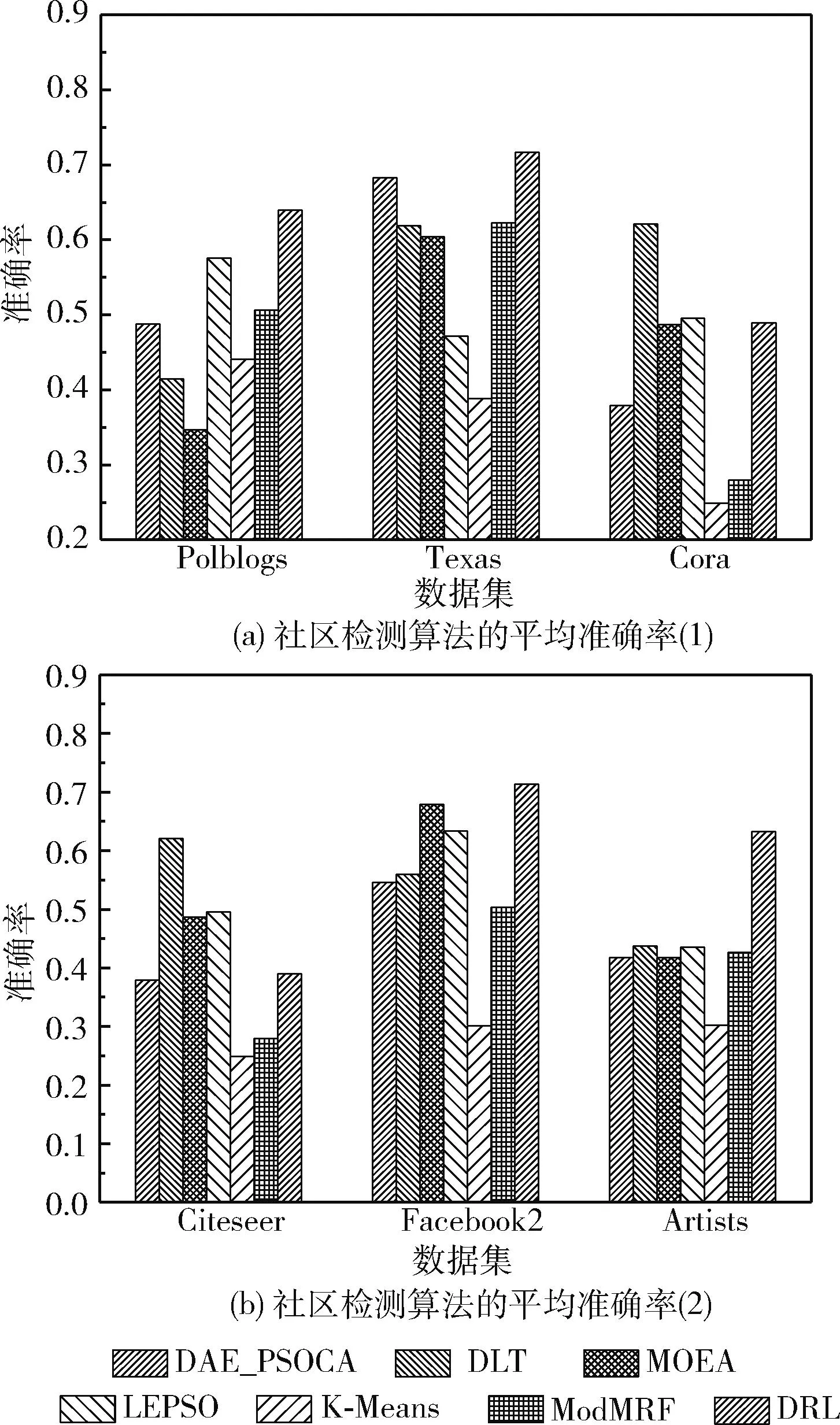
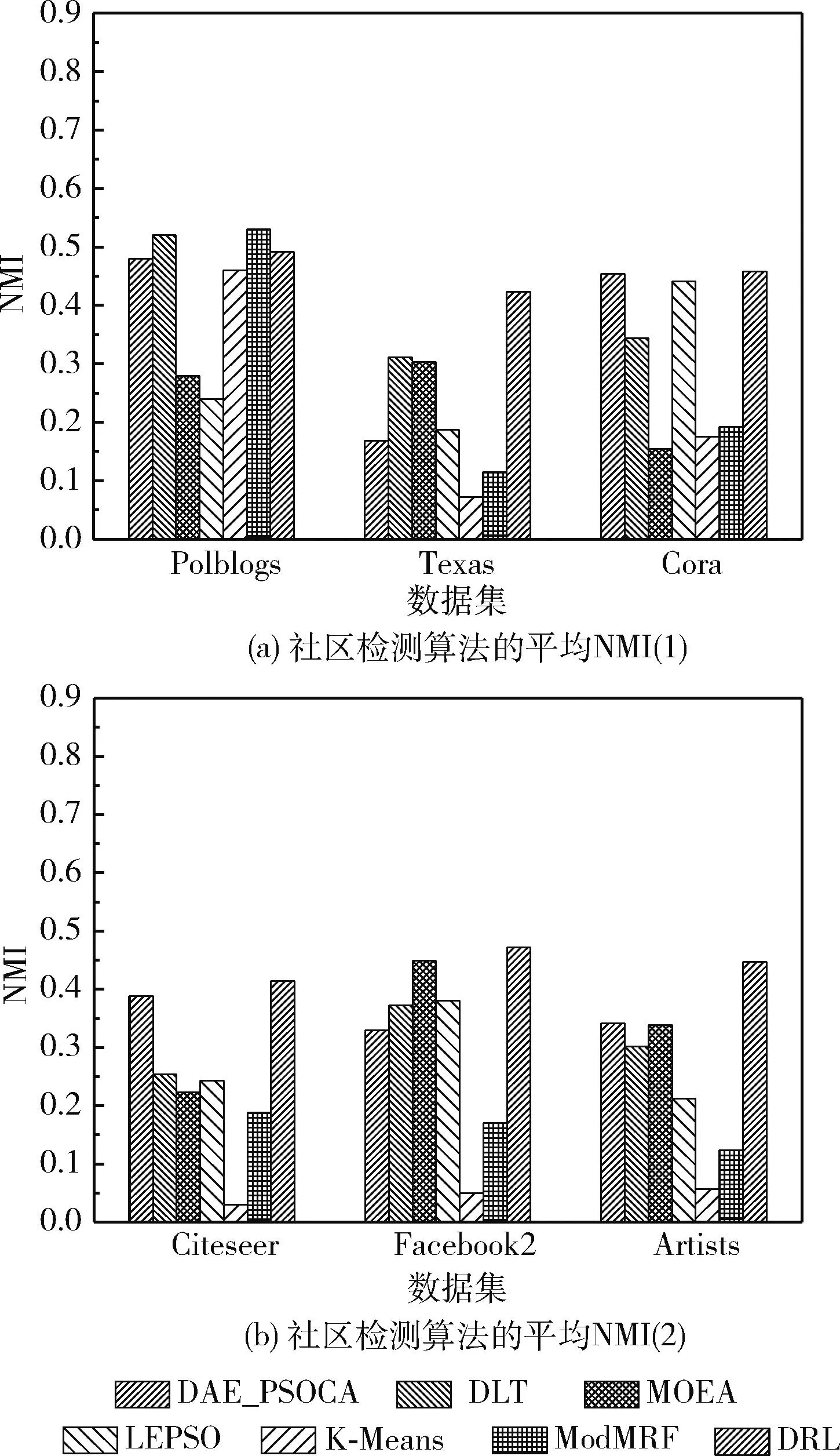
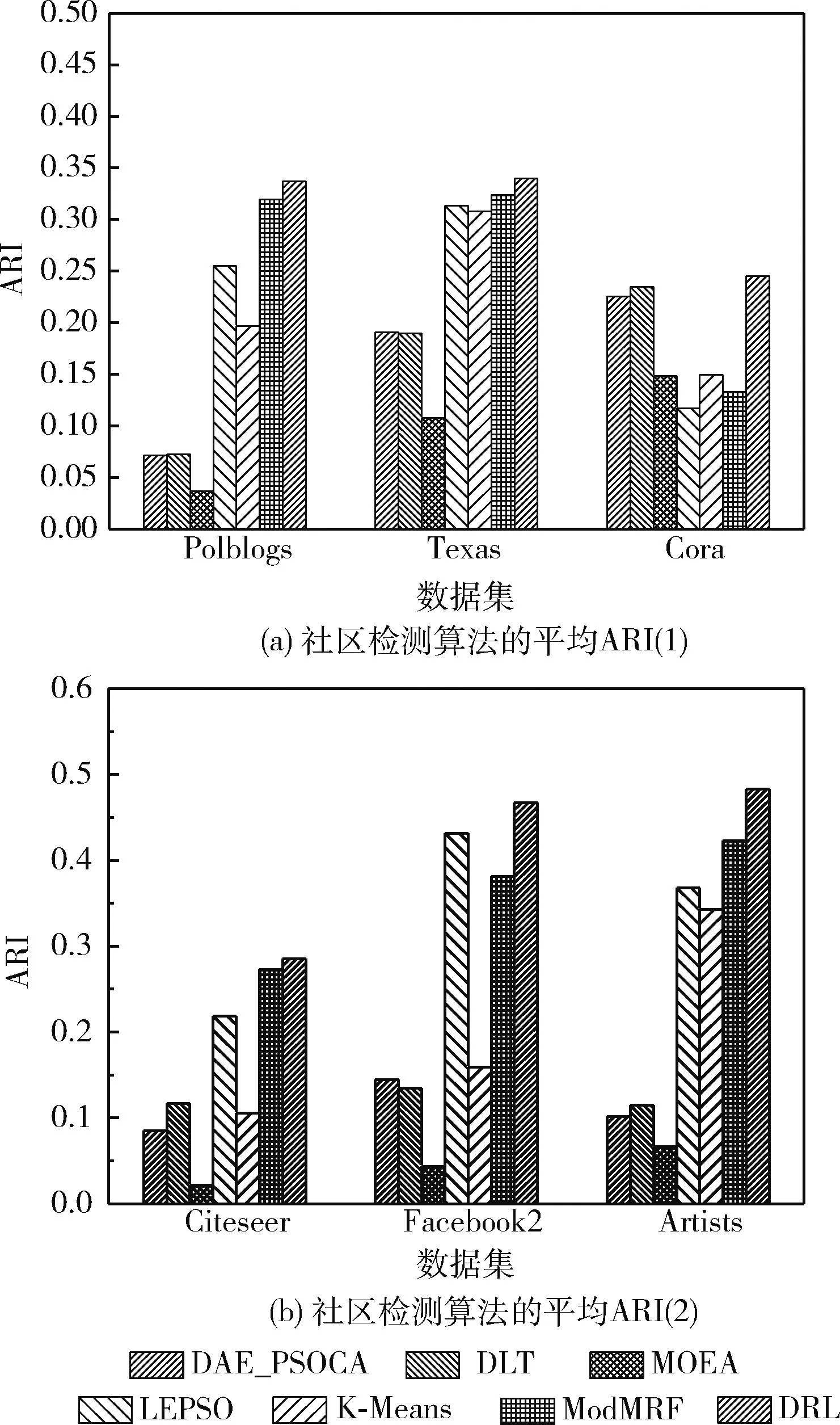
(19) If (GModularity (20)GModularity←LModularity; //更新全局模块度 (21) Endif (22)Endfor 以一个简单实例描述社区局部结构优化算子的处理过程:一个初始化的网络社区结构如图6(a)所示,节点3的外部连接数为2个,节点7与节点8的外部连接数为1个,其它节点的外部连接数均为0,因此该网络的外部连接列表降序排列为 {3,7,8,0,0,0,0,0,0,0}。 首先,遍历列表的第一个节点,计算节点3与其它社区内邻居节点的相似性SS(),如果SS(v3,v7)>SS(v3,v8), 那么将v3由社区a迁移至社区b中,该过程如图6(b)所示。如果SS(v3,v7) 图6 社区局部优化算子 本文利用深度强化学习的感知能力与自适应决策能力决定网络的社区数量与社区结构,将社区检测问题建模为一个优化问题,其目标是最大化网络的模块度密度函数。Q-learning技术是一种基于自动agent的强化学习技术,该技术通过不断采取动作与环境交互,以最大化累积的总奖赏。Q-learning的工作原理如图7所示。Agent根据当前状态St感知环境的变化,Agent根据当前环境选择执行一个动作At,环境向Agent反馈一个奖赏,并将状态变量St更新为St+1,该状态变量迁移的概率可表示为P(St,At,St+1)。 Q-learning的目标是学习最优策略π(At|St), 以最大化当前的累积奖赏。 图7 Q-learning的工作原理 Q-learning框架中的状态迁移过程可表示为 (10) 式中:φ∈[0,1] 为奖赏折扣因子。 给定一个策略π,Q-value函数可估计状态St下动作At的累积奖赏期望值,Q-value函数可表示为:Qπ(St,At)=E[R|St,At,π]。 将每个状态下Q-value值最高的策略作为最优策略,将最优Q-value记为 Q*(St,At)=max(Qπ(St,At)) (11) Q-value函数的计算方法记为 Qπ(St,At)=Rt+φ·Q*(St+1,At+1) (12) Q-value的动态更新方法记为 Qπ(St,At)←Qπ(St,At)+η·Δ (13) 式中:η∈[0,1] 为学习率,Δ为时间差分误差。Δ的计算方法如下 Δ=Rt+φ·maxAt+1[Qπ(St+1,At+1)-Q(St,At)] (14) Q-learning框架将Q-value保存于一张查找表中,如果可选状态的数量过大,那么根据查找表搜索最优策略的速度较慢。深度强化学习中的DQN(deep q-network)模型可加快Q-learning的学习速度,DQN采用神经网络估计强化学习的Q-value。DQN模型的输入为状态向量,输出为Q-value,采用均方偏差函数作为DQN的损失函数。DQN的损失函数可定义为 L(Θt)=(QT-Q(St,At,Θt))2 (15) QT=Rt+φ·maxAt+1Q(St+1,At+1,Θt) (16) 式中:Θt为第t次迭代的神经网络参数。 通常神经网络作为损失函数存在收敛稳定性不足的问题,本文采用经验重放机制改善DQN的收敛稳定性。该机制采用两个相同结构的神经网络,两个网络的超参数分别记为Θ与Θ′,前者用于计算Q-value,后者用于保存训练过程中的全部Q-value,每隔C个时间步将Θ更新为Θ′。该机制的原理如图8所示。 图8 深度强化学习的经验重放机制 3.2.1 状态信号 状态St表示复杂网络被划分成P个社区,将St表示为一个向量形式 St=[wt,1,wt,2,…,wt,P] (17) 式中:向量元素wt,i=[vm,…,vn] 表示第i个社区包含的节点集。 设Sp表示指定社区p对应的全部状态集,Sp可表示为 Sp=[S1,p,S2,p,…,ST,p] (18) 式中:T为社区p的状态数量,即该社区在每个时间步包含的节点集。 3.2.2 动作信号 将AgentAt,p的动作表示为一个向量形式,表示社区局部优化算子(第3.1.2部分)的节点迁移方案,动作信号可表示为 At=[ct,1,ct,2,…,ct,P] (19) 式中:P为发生迁移的节点数量,t为当前的时间步,动作信号的元素ct,i为迁移方案向量,如ct,i=[1,2,3] 表示节点1从第2个社区迁移到第3个社区。 3.2.3 奖赏信号 相较于广义密度函数,模块度密度函数对社区尺寸差异大的网络效果更好,因此采用复杂网络的模块度密度函数作为Agent的奖赏函数。奖赏函数可表示为 (20) 式中:Gi表示复杂网络G第i个社区的子图,l为网络的社区数量,Vi为子图Gi的顶点集。 模块度密度值越大,说明网络的社区划分越准确。Q-learning中Agent的任务是寻找状态集与动作集之间的最优映射关系,该最优映射集关系最大化累积奖赏,即最大化网络的模块度密度。 实验使用Gephi version 0.9.2软件分析社交网络数据,使用Python 3.6实现文中相关算法,编程环境为PyCharm与Eclipse集成的开发平台。PC机的配置为Intel Core i7-11700,主频为2.5 GHz,内存为32 GB,操作系统为Ubuntu 18.04。 为评估本文算法的有效性,使用6个不同规模的真实社区检测数据集,分别为Polblogs、Texas、Cora、Citeseer、Facebook2与Artists。一方面,所选数据集在社区数量、连接数量与节点数量上均有所区别,具有较好的多样性;另一方面,所选数据集被广泛用作benchmark数据集,便于进行对比实验。 表1总结了各数据集的相关属性,Polblogs、Texas、Cora与Citeseer属于中小规模的网络,Polblogs与Texas数据集的连接较密集,Cora数据集的连接较稀疏。Citeseer数据集的连接最为稀疏,难以通过连接直接度量出节点间的相似性。Facebook2与Artists属于大规模的网络,两个网络的连接较密集,Facebook2的社区结构较简单,Artists的社区数多达20个,社区检测的难度更大。 表1 社区检测数据集的相关属性 为便于进行对比实验,采用3个常用指标评估各社区检测算法的性能,分别为准确率、正则化互信息(norma-lized mutual information,NMI)与兰德指数 (adjusted rand index,ARI)。 准确率评价了社区检测结果中被正确划分的社区比例。准确率越高,社区检测算法的性能越好。准确率的计算公式如下 (21) 式中:n为节点数量,Ci为节点i的正定社区,C′i为本文算法为节点i分配的社区。k(x,y) 为一个指示函数,如果x=y,那么k(x,y)=1, 否则k(x,y)=0。 NMI能客观地评价检测算法所划分社区与正定社区之间相比的准确度。NMI值越高,社区检测算法的性能越好。NMI的计算公式如下 NMI(A,B)= (22) 式中:A与B分别为实际社区与检测社区,NMI值越高说明社区检测的性能越好。 ARI通过比较社区检测结果与正定社区划分之间的误差来评价社区检测的正确性。ARI值越高,社区检测算法的性能越好。ARI的计算公式如下 (23) 式中:E为ARI的期望值,E的取值范围为[-1,1]。Rand()函数的计算方法如下 (24) 式中:A表示聚类与类之间邻居对的数量,B表示邻居对的数量被分成聚类与分类。 选择6个社区检测算法与本文算法进行对比实验,横向评估本文算法的性能。对比算法如下: DAE_PSOCA[16]:该算法是基于深度自编码器与粒子群优化算法的复杂网络社区检测算法。它利用粒子群优化算法训练深度自编码器,缓解深度自编码器在复杂网络上容易收敛于局部极值的问题。 DLT[17]:该算法是基于自编码器与卷积神经网络的社区检测算法。它包含网络邻接矩阵重建、空间特征提取以及社区检测3个步骤。利用卷积神经网络提取网络的空间结构特征,利用自编码器重建邻接矩阵,以此增强社区检测所需的相关信息。 MOEA[18]:该算法是基于多目标演化算法的社区检测算法。它通过改进遗传变异算子与交叉算子提高对社区模块度的优化效果。 LEPSO[19]:该算法是基于协作粒子群优化的动态社区检测算法。它通过多粒子群间协作机制解决社区不平衡与不显著导致社区划分不准确的问题。 K-Means[20]:该算法是基于K-means聚类的社区检测算法。它通过余弦距离度量节点间的相似性,采用K-means聚类算法对复杂网络进行无监督聚类处理。 ModMRF[21]:该算法是基于乘积和信息传递置信度传播的社区检测算法。它使用模块度作为能量函数驱动置信度传播过程。 将式(7)中k-近邻的k参数设为网络的平均度数,权重因子γ设为0.1,Nth的设为网络的平均度数,Trymax设为30。在TensorFlow框架与Keras深度学习库上编程实现文中所提及的神经网络,在MATLAB 2019B上编码非深度学习算法。神经网络训练过程终最大epoch次数为500。 DRL在各数据集上训练的损失曲线如图9所示。观察图中曲线可知,Cora与Citeseer两个数据集大约经过150次epoch达到收敛,Polblogs数据集大约经过200次epoch达到收敛,Texas数据集大约经过350次epoch达到收敛,Facebook2数据集大约经过300次epoch达到收敛,Artists数据集大约经过250次epoch达到收敛。 图9 各数据集训练的损失曲线 各社区检测算法在6个benchmark数据集上的平均检测准确率结果如图10所示。DAE_PSOCA算法在Texas数据集与Artists数据集上的检测准确率较高,在其它4个数据集上的检测准确率较低。Texas与Artists数据集的网络连接较密集,DAE_PSOCA算法利用深度自编码器强大的感知能力提取网络连接的信息,利用粒子群优化算法缓解深度自编码器在复杂网络上容易收敛于局部极值的问题,在Texas与Artists数据集上性能较好。DLT算法在Texas数据集与Citeseer数据集上的检测准确率较高,在其它4个数据集上的检测准确率较低。DLT算法利用卷积神经网络提取网络的空间结构特征,提取了Texas数据集密集的连接信息,因此在Texas数据集上性能较好。此外,DLT算法利用自编码器重建邻接矩阵,增强了社区检测所需的相关信息,因此在Artists数据集上性能也较好。MOEA算法与LEPSO算法均为基于启发式算法优化复杂网络模块度的社区检测算法,比较这两个算法在6个数据集上的实验结果可得出结论,多目标演化算法的优化效果好于多目标粒子群算法。ModMRF用置信度传播代替传统标签传播,将模块度作为驱动传播的能量函数,该算法的准确率较低。本文算法利用新的相似性度量指标度量了节点在网络拓扑结构上的相似性,利用深度强化学习模型发现网络的社区结构,并通过社区局部优化算子改善社区边界划分的准确性。本文算法在Polblogs、Texas、Facebook2与Artists共4个数据集上均取得了最优的检测准确率,且大幅领先于其它对比社区检测算法,而在Cora与Citeseer两个数据集上的检测准确率低于DLT算法,本文算法对连接密度低的网络性能较低,对连接密度较高的网络性能较好。其原因在于:本文算法在社区初始化阶段以网络度数为社区中心判定依据,在社区局部优化算子中以网络连接为节点迁移依据。综上所述,连接过少难以发挥本文算法的优势,容易出现误判与漏判的情况;而连接密集度越高,本文算法的优势越大。 图10 社区检测算法的平均准确率 各社区检测算法在6个benchmark数据集上的平均检测NMI值如图11所示。DAE_PSOCA算法与DLT算法在Artists数据集上的NMI结果较好,在其它5个数据集上的NMI结果较低。MOEA在Texas、Facebook2与Artists数据集上的NMI结果较高,LEPSO则在Cora数据集上的NMI结果较高,由此可知基于启发式的社区检测算法发现的社区结构与正定社区结构的偏差较大。ModMRF用置信度传播代替传统标签传播,将模块度作为驱动传播的能量函数,该算法高连接密度小规模数据集Polblogs上的NMI性能最佳,在其它大规模数据集或低连接密度数据集上的NMI性能较低。本文算法利用新的相似性度量指标度量了节点在网络拓扑结构上的相似性,利用深度强化学习模型发现网络的社区结构,并通过社区局部优化算子改善社区边界划分的NMI值。本文算法在6个数据集上均取得了最优的检测NMI值,由此可知,本文算法发现的社区结构与正定社区结构最为接近。 图11 社区检测算法的平均NMI 各社区检测算法在6个benchmark数据集上的平均检测ARI值如图12所示。DAE_PSOCA、DLT、MOEA这3个算法在6个benchmark数据集上的平均检测ARI值较低,由此可知,这3个算法发现的社区结构与正定结构存在较大的误差。ModMRF用置信度传播代替传统标签传播,将模块度作为驱动传播的能量函数,该算法发现的社区结构误差较小,但产生较多的小尺度社区,所产生的社区数量与正定社区结构存在较大的偏差。本文算法在6个数据集上均取得了最优的检测ARI值,由此可知,本文算法发现的社区结构与正定社区结构的误差最小。 图12 社区检测算法的平均ARI 为提高复杂网络社区检测的准确性,本文利用深度强化学习为复杂网络的社区检测问题提出新的解决思路。第一阶段基于网络拓扑结构初始化社区结构,第二阶段基于深度强化学习对网络社区结构进行微调与优化,利用深度强化学习强大的感知能力与决策能力提高社区结构的准确性。该算法在社区初始化阶段以网络度数为社区中心判定依据,在社区局部优化算子中以网络连接为节点迁移依据。因此,连接过少难以发挥本文算法的优势,而连接密集度越高,本文算法的优势越大。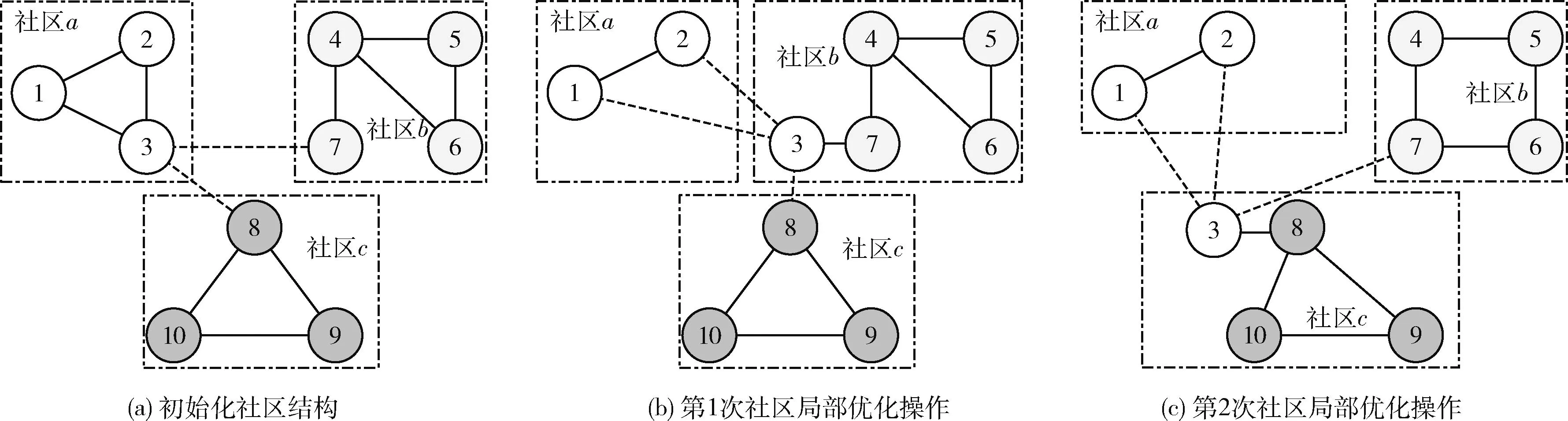
3.2 深度强化学习
4 实验与结果分析
4.1 实验数据集

4.2 性能评价指标
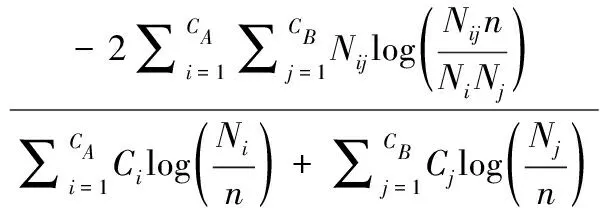
4.3 对比算法
4.4 参数设置与训练
4.5 实验结果与分析
5 结束语

