基于可逆水印的神经网络模型完整性验证算法

杨奥松，王 雷，曹仰杰，庄 岩+，李 颉，3，任红军

(1.郑州大学 网络空间安全学院，河南 郑州 450001；2.汉威科技集团股份有限公司 汉威研究院，河南 郑州 450001；3.上海交通大学 计算机系，上海 200030)

0 引 言

深度神经网络已被广泛应用于各个领域，为了便利深度学习模型的应用，实现自动化部署，许多IT公司为深度学习模型提供基于云的训练和服务，通常被称为机器学习即服务[1](machine learning as a service，MLaaS)。使用在云中部署的模型时，模型完整性的保障是用户关注的重点，复杂网络的训练需要经历多个阶段，在此期间易遭受非法访问，攻击者可能会利用网络或存储协议中的潜在漏洞[2]访问传输中或已部署的目标模型，修改其参数以达到攻击目的。例如，攻击者可能会在模型中注入后门[3]，使得模型可以表现出攻击者想要的行为，或者利用数据中毒攻击[4]，使用带错误标签的数据对目标模型进行恶意微调，使得模型的性能严重下降。

现有模型完整性验证方法大多基于修改模型参数，大致分为两种：一种是黑盒方法[5，6]，利用模型特有的决策边界，使模型对修改敏感，从而验证模型的完整性，然而黑盒方法只能判断模型的完整性是否遭受到了攻击，无法评估模型遭受攻击程度即失真度；另一种是白盒方法，Botta等[7]在模型参数频域中嵌入脆弱水印，根据提取的水印差异度量模型完整性失真值。原则上，即使网络参数的微小变化也可能影响网络性能，任意篡改可能导致严重的破坏性事故。因此，本文提出了一种快速神经网络模型完整性验证算法Fast-MIV，在不影响原始模型性能的情况下实现卷积神经网络(convolutional neural network，CNN)的可逆水印嵌入，可完全恢复模型参数。基于模型剪枝理论，构建目标模型的待嵌入参数序列，嵌入哈希加密信息，在高保真度要求下，可实现模型参数的完全恢复，并提出了一种新的评价指标来评估模型的完整性失真度。

1 相关工作

He等[5]构建对神经网络的最小改动敏感的特殊样本，在验证阶段将此类样本输入更改后的模型将产生与预期不同的输出，从而能够识别网络已被更改。Zhu等[6]借助触发器思想[8]，对模型进行两阶段的交替训练，使得模型能够对特定的触发器序列，生成预定义的预测结果，这种触发模式是脆弱的，一旦模型遭受微调或其它完整性威胁，对触发器图像的分类精度就会严重下降，因此可用于验证模型的完整性。然而模型重新训练往往是一个复杂的过程，研究表明，基于触发器的方法很容易被检测[9]甚至删除[10]。

Botta等[7]采用脆弱水印来保护网络结构和权重，将脆弱水印嵌入由KL(Karhunen loève)变换定义的秘密频域，模型一旦遭受篡改，所提取的脆弱水印会和原嵌入水印产生差异，从而验证模型的完整性。然而大多任务对模型质量有很高的要求，要求嵌入水印后，模型原始性能不会受到影响，在高保真度场景下，模型参数的篡改造成模型性能差异是不可取的。

2 本文方法

2.1 问题定义

形式上，考虑模型M的m层卷积层C={c1，c2，…，cm}， 其中第i层所有的参数为Wi∈Rni×ni+1×k×k， 其中ni为输入通道(channel)数，ni+1为输出通道数，k为卷积核(kernel)的尺寸。将待嵌入水印信息，利用哈希加密算法转化为二值向量b={b1，b2…bn}，bi∈{0，1} 嵌入Wi中，其中b的长度取决于哈希算法。

首先，利用加密哈希算法hash生成b， 为了尽可能减小验证过程对模型原始任务的影响程度，同时将水印嵌入模型参数中，使用模型剪枝方法，筛选对模型原始任务影响较小的位置构建待嵌入参数序列。

在嵌入阶段，使用可逆编码算法ε将b嵌入到模型M中

M′=ε(M，b)，M′≈M

(1)

生成的模型M′， 在性能上接近原模型M， 不影响模型的原始分类任务或其它任务。

然后，在提取阶段，使用ε对应的解码算法φ提取水印信息

(2)

在高保真度要求的场合下，可以将M′恢复成M。

为了验证模型的完整性，首先对目标模型使用提取器φ提取加密信息b′， 然后与保留的b进行对比，如果b′=b， 则可认为模型的完整性没有遭到破坏。

具体流程图1所示：在待保护的预训练模型上筛选卷积层，借助模型剪枝理论，筛选filter进行预处理并构建待嵌入水印的参数序列，使用差值扩展可逆水印嵌入加密后的信息，具体的算法在2.2、2.3和2.4小节介绍。

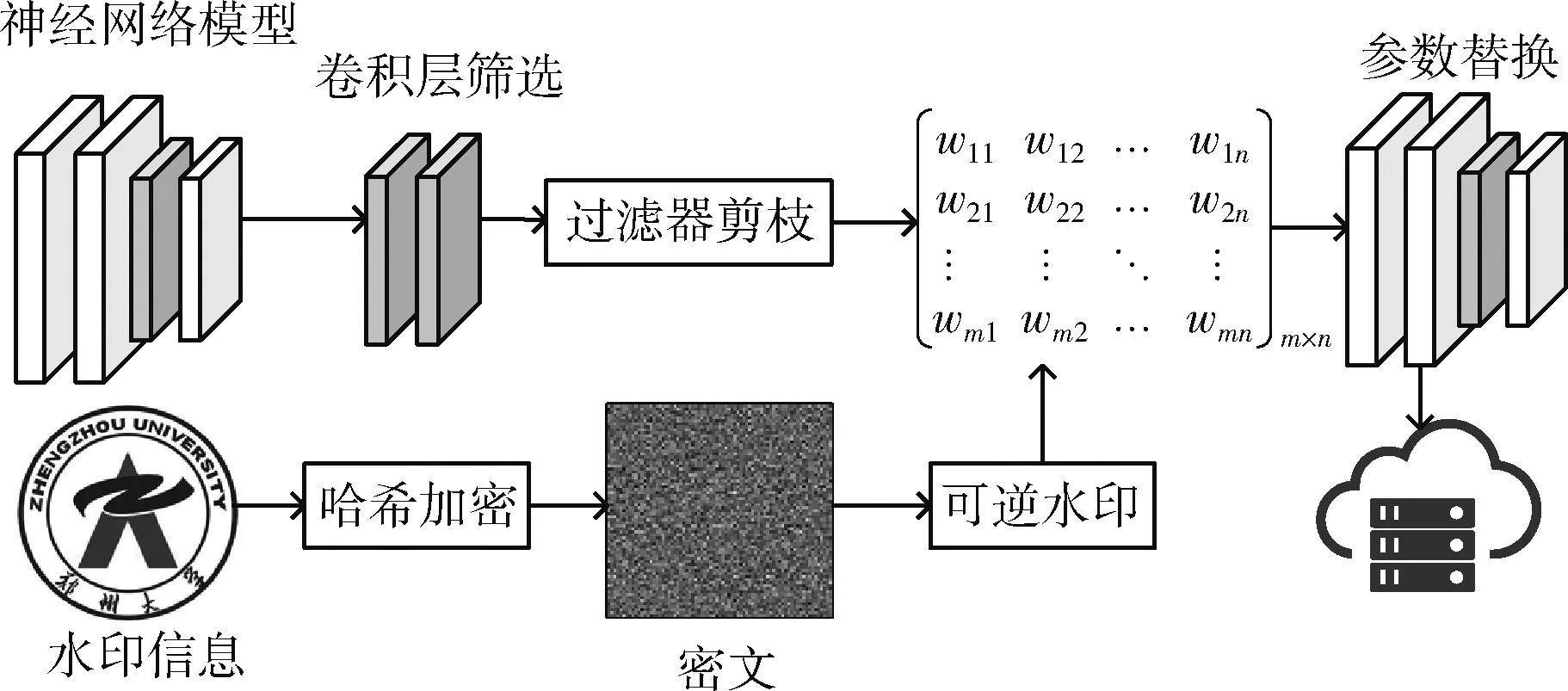
图1 Fast-MIV算法流程

2.2 构建参数序列

训练好并部署的模型具有固定的权重参数，这些权值决定了模型的性能，复杂网络模型存在大量冗余的参数，将这些神经元去除后仍可以表现出与原模型同等的模型表达能力[11]。

本文使用滤波器剪枝，又称为结构化剪枝，进行filter筛选并构建待嵌入参数序列，筛选倾向于产生具有弱激活的特征映射filter，因此在这些filter进行水印嵌入对模型原始任务造成的影响会尽可能小。

设模型M第i层卷积层的输入通道数为ni， 应用ni+1个filter，第j个filter的尺寸为Fi，j∈Rni×k×k， 将3D输入特征图转换为3D输出特征图Xi+1∈Rni+1×hi+1×wi+1， 每个filter由ni个2D卷积核Ki∈Rk×k组成，具有固定的权值，该层的所有滤波器组成核矩阵(Kernel matrix)Fi∈Rni×ni+1×k×k。

设模型的单层卷积层具有ni个filter，每层卷积层有ni×ni+1×k×k个嵌入位置。本文选定模型待嵌入单层或多层，利用3种方法筛选卷积层中单个或多个filter进行参数序列的构建，并在实验中进行效果评估。

(1)随机法(random)：随机选择filter进行嵌入。

(2)L1范数法：

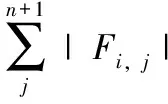
(3)几何中值(geometric median，GM)法：

GM是欧氏空间中数据中心的经典鲁棒估计量，常被用于点云的曲面重建和骨架提取，He等[13]提出GM进行filter修剪，从而筛选出最可被替代的filter，其中GM被定义为：给定n个点a(1)，a(2)…a(n)∈R， 找到一个点x*∈Rd， 使其欧氏距离之和最小化

(3)

对于选定第i层卷积层内所有filter，计算其GM为

(4)

其中，g(x) 为

(5)

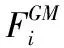
2.3 预处理

图像的像素值一般是0到255的整数，而神经网络模型的权重参数都是浮点数，对于应用于图像的可逆水印技术，模型参数不具有图像像素的相关性。为了构建与图像更相似的参数矩阵，将上一节构建的参数序列进行重新排列

(6)

所得到的参数序列并不能直接应用于承载水印，因此，对参数序列进行预处理，从Ai的每个元素截取两位数，假设wi，j∈Ai， 具体的截取位置如下

(7)

式中：从n1开始，表示小数点后的第一个非零数字，对于不同的wi，j，n1的起始位置不同，截取n1n2两位数字足以嵌入水印信息，容易得出，n1×10+n2∈[0，99]。

2.4 可逆数据隐藏算法

本文使用差值扩展(difference expansion，DE)进行可逆水印嵌入。具体地，设 (x，y) 是序列中相邻的两个值。定义其平均值l和差值为h为

(8)

将T比特的待嵌入二值向量b， 应用最低有效位(least significant bit，LSB)嵌入到DE生成的差值h中，新的差值h′为

h′=2×h+b，b∈[0，1]

(9)

嵌入阶段，通过l和h′计算得到更改后的两个数值x′和y′

(10)

使用 (x′，y′) 替换序列中的 (x，y)， 可嵌入一位信息，重复这个过程完成水印嵌入，式(8)、式(9)、式(10)组成ε算法。

提取阶段，可以仅根据修改后的 (x′，y′) 恢复出原始 (x，y)。 提取过程如下

根据新的差值h′计算新的均值l′为

(11)

由于在除法时使用向下取整，将式(10)带入式(11)可知，l′=l。 再根据所得h′可恢复出 (x，y) 的值，提取到所有信息后，再组合成水印。

如果模型是完整的，在解码过程可以完整提取嵌入信息b′。 由于采用的水印是脆弱的，当模型权重参数遭受篡改时，提取的水印信息会与嵌入信息b不同，从而判断模型遭受完整性破坏程度。

3 实验结果与分析

3.1 实验设置

使用MD5和安全散列算法(Secure Hash Algorithm 2，SHA-2)生成水印信息。应用SHA-256安全散列算法可以将任意待嵌入信息，例如产品序列号和模型版权所属者身份信息等压缩加密为定长的二值信息。由于其抗碰撞的优良特性，这些哈希加密算法已被广泛使用在密文领域。

ImageNet数据集由1000个类的彩色图像组成，被广泛应用于图像识别领域。本文采取在ImageNet上的4个预训练的网络VGG19[16]、Densenet-121[17]、ResNet-50[18]和Inception-v3[19]作为目标模型。上述模型均为ImageNet大规模视觉识别挑战赛(imagenet large scale visual recognition challenge，ILSVRC)中的经典模型。为了评估本文所提出的完整验证算法Fast-MIV的性能，在实验中随机选取100个类的一万张图片组成测试集进行评估。使用随机方法作为基线，评估后两种构建待嵌入参数序列方法的性能。

3.2 评价指标

本文采用峰值信噪比(peak signal to noise ratio，PSNR)评估filter嵌入水印前后对应生成的激活特征图损失，计算公式如下

(12)

(13)

其中，MSE为均方误差，PSNR是常用的衡量图像质量的指标。

由于所使用嵌入水印的脆弱性，一旦攻击者修改模型，新提取的水印信息会与原嵌入的水印信息有所不同。因此，本文提出一个新的失真度指标ACCdis， 利用原嵌入水印和验证时提取到的水印差异来评估模型的完整性损失度，计算公式如下

(14)

其中，⊙表示同或，xi，j和yi，j分别表示嵌入和提取的二值水印，n为水印长度。式(14)通过水印差异，反映模型遭受篡改的程度，如果ACCdis=1， 视为模型完整性没有遭受破坏；否则，认为模型的完整性遭受破坏。

3.3 实验结果

为了验证Fast-MIV在不同模型上的性能，在选定的4 个模型VGG19、DenseNet-121、ResNet-50和Inception-v3上进行嵌入对比，选择模型最后一层卷积核大小为3*3的卷积层，分别使用3种方法筛选filter嵌入由SHA-256加密相同内容信息生成的256位水印信息，结果见表1。

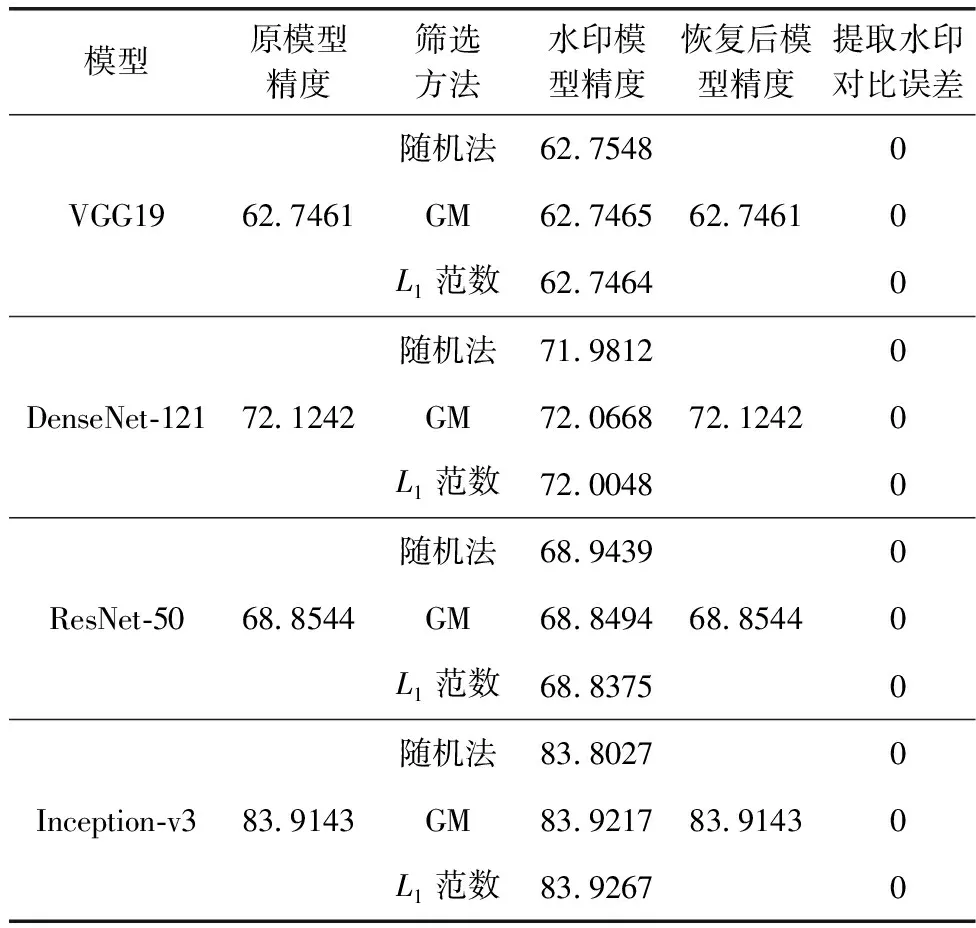
表1 多模型嵌入水印损失比较/%

从表1中可看出，上述模型嵌入水印不会影响模型的原始性能，精度损失在0.1%以内，且可完全提取水印信息同时恢复模型参数以恢复模型原始性能。对于ResNet-50上使用的随机参数序列筛选方法，水印模型的分类精度甚至提高了0.01%，这是由于神经网络具有冗余性。

为探究Fast-MIV多层嵌入的性能，在4个目标模型上顺序筛选多层卷积层，使用3种剪枝方法分别构建待参数序列，使用同样的方法进行水印嵌入，结果见表2。

表2 多层嵌入效果比较/%

从表2可看出，将水印嵌入单层或多层卷积层不会显著影响模型分类精度，并且使用差值扩展法可完全恢复模型参数，Fast-MIV可应用于深度卷积网络。

为探究Fast-MIV的可嵌入容量，即水印长度对模型精度的影响，将不同长度的水印嵌入到VGG19的最后一层卷积层中，结果见表3。

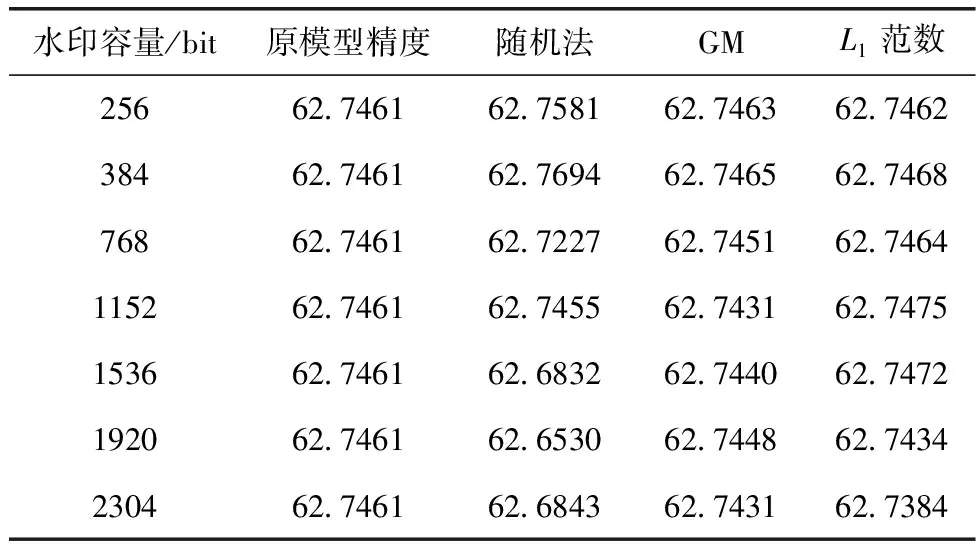
表3 VGG19不同水印信息容量比较/%

表3可知，随着水印长度增加，模型的分类性能会有所下降，但影响较小。当水印信息足够长时，使用GM法和L1范数法构建待嵌入参数序列，相比于随机方法，可有效降低嵌入信息对原始模型任务的影响，水印容量越大GM法和L1范数法对模型的性能影响相对于随机法越小。

为了直观看出模型嵌入水印前后对filter生成激活特征图的影响，在VGG19模型上筛选低维度卷积层，计算其输出特征图差异，并计算PSNR，如图2所示。

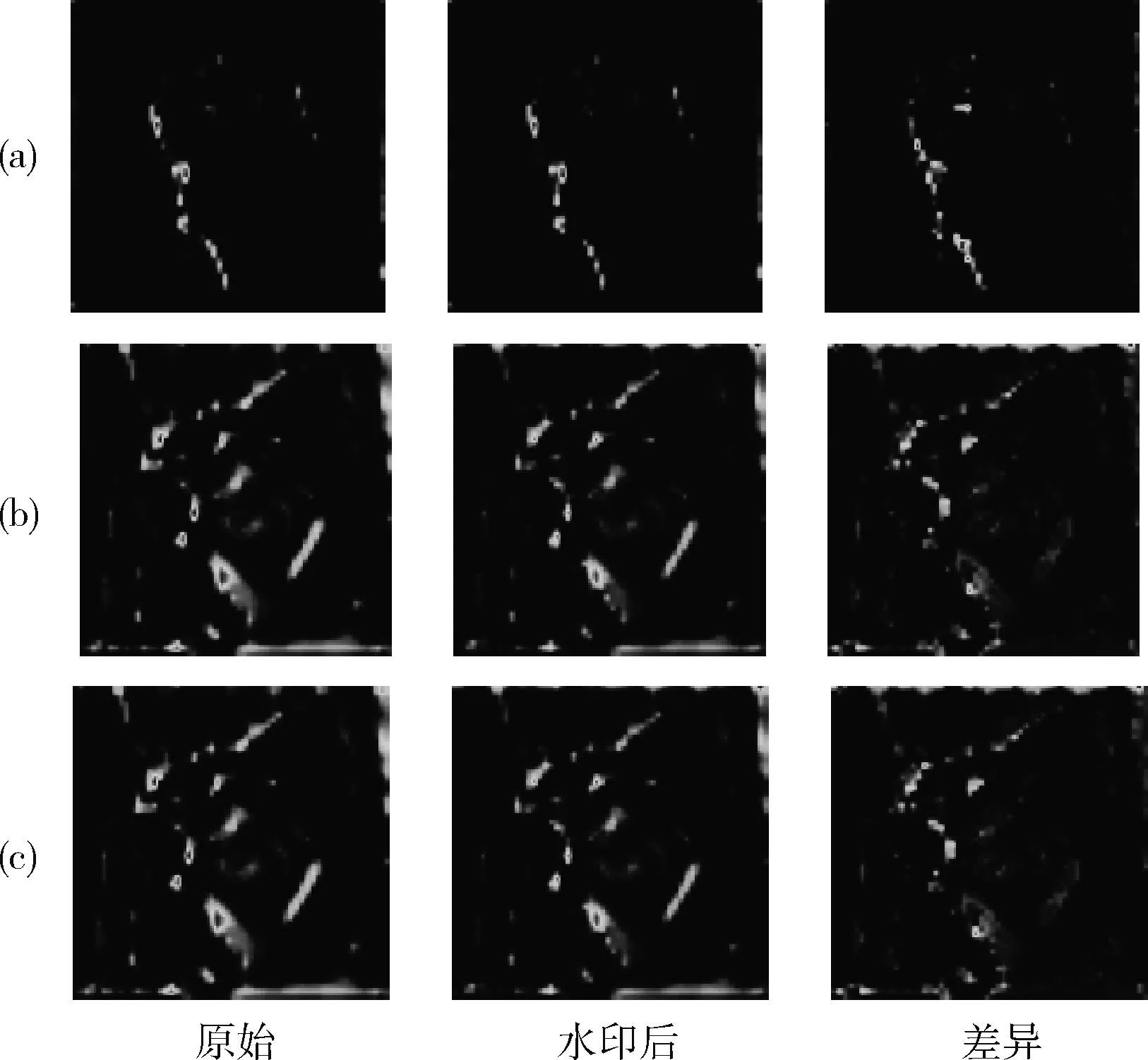
图2 VGG19上低维度卷积层激活特征图对比

图2中，横轴第一列为原模型对应卷积层输出特征图，第二列为嵌入水印后模型的输出特征图，第三列为其差异，纵轴表示3种对应的构建方法，图2(a)为随机法，图2(b)为GM法，图2(c)为L1范数法。平均PSNR在65 db以上。

Song C等[21]采用最低有效位(least significant bit，LSB)将水印信息嵌入参数的空间域最低位面中，Abuadbba A等[22]采用离散小波变换(discrete wavelet transformation，DWT)将模型每层的参数和应用SHA算法加密后的信息随机嵌入该层的参数频域中，通过提取频域水印信息进行对比以达到保护模型完整性的效果，Li Y等[23]采用直方图位移实现了JPEG图像的数据隐藏，并利用最优阈值选择了一个适合于嵌入秘密信息的离散余弦变换(DCT)系数子块。为了评估Fast-MIV的性能，在VGG19模型上进行对比，其中Fast-MIV选取3种嵌入方法的平均值，在模型的每一层嵌入256 bit水印信息，将Li Y等[23]的图像水印方法迁移到模型水印中，结果见表4。

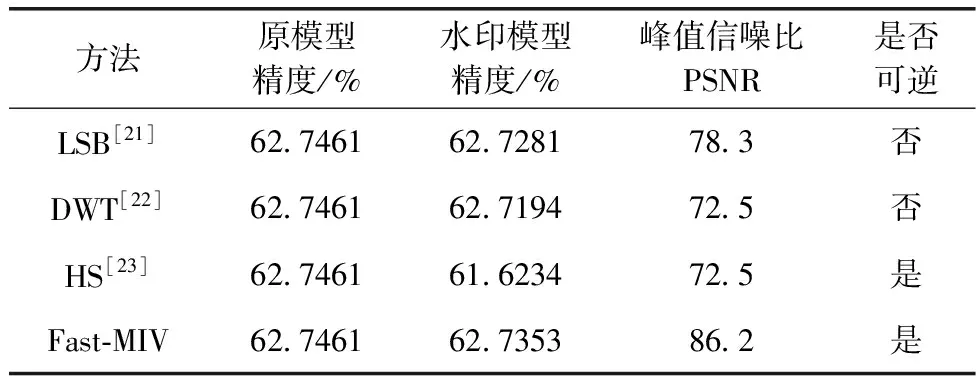
表4 VGG19不同水印方法性能对比

从表4可以看出，Fast-MIV对原模型的性能影响更小，这是由于所提出的3种构建参数序列的方法相比DWT[21]和HS[23]更好利用了模型的冗余性，使用的预处理方法降低了对参数的修改程度，使得PSNR更高，HS[23]在JPEG图像上实现的可逆水印，也未考虑到模型参数筛选问题。相比于LSB[21]和DWT[22]，Fast-MIV使用可逆水印，可以恢复模型参数，以达到对模型的完全恢复。

3.4 完整性验证

微调是攻击者常用且有效的破坏模型完整性方法，只需要少量的新数据即可对模型进行改动[4]。例如数据中毒攻击，最常见的做法是使用带错误标签的中毒数据对模型进行微调，以降低模型的性能。为了在更短的微调批次达到较好的效果，通常的做法是冻结目标网络的前几层，只对最后几层进行微调，因此在本小节实验中，水印被添加到模型的最后一层。

实验中，学习率设置为0.001，在微调过程中使用带动量的随机梯度下降算法作为优化函数，每个训练批次的规模设置为64，使用1200张图片构建中毒数据集对模型微调以进行数据中毒攻击，其中带错误标签的数据占比20%，其它沿用原模型的设置。随着训练的批次增加，计算失真度ACCdis， 结果如图3所示。

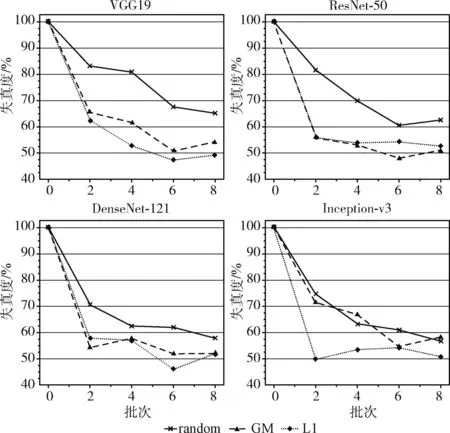
图3 多模型数据中毒攻击对比

图3可知，即使只微调了几个批次，水印的失真度也会产生明显下降，这表明模型遭受的完整性破坏能被检测出来，Fast-MIV在应对数据中毒攻击上具有良好的效果。

文献[6]提出一种基于触发器的模型完整性验证方法Fragile[6]，构建触发器测试集，依据测试集精度指标下降程度判断模型完整是否遭到破坏。Fast-MIV在cifar-10和cifar-100数据集上预训练的ResNet-50上采用与文献[6]同样的中毒数据集进行数据中毒攻击，其中Fast-MIV嵌入的水印和文献[6]设定的触发器的大小保持一致，使用中毒数据集微调模型，记录微调批次，当批次指标下降为80%以下，视为模型完整性遭到破坏，结果见表5。

表5 ResNet-50完整性检测结果(批次)

结果表明，相比Fragile[6]，Fast-MIV只需更少微调批次即可检测到模型完整性遭受破坏，具有更高灵敏度。

为进一步验证Fast-MIV能否支持结构化验证，即是否能够检测模型的结构完整性，对模型进行剪枝攻击，随机将某些神经元参数置零，并计算失真度ACCdis， 结果如图4所示。

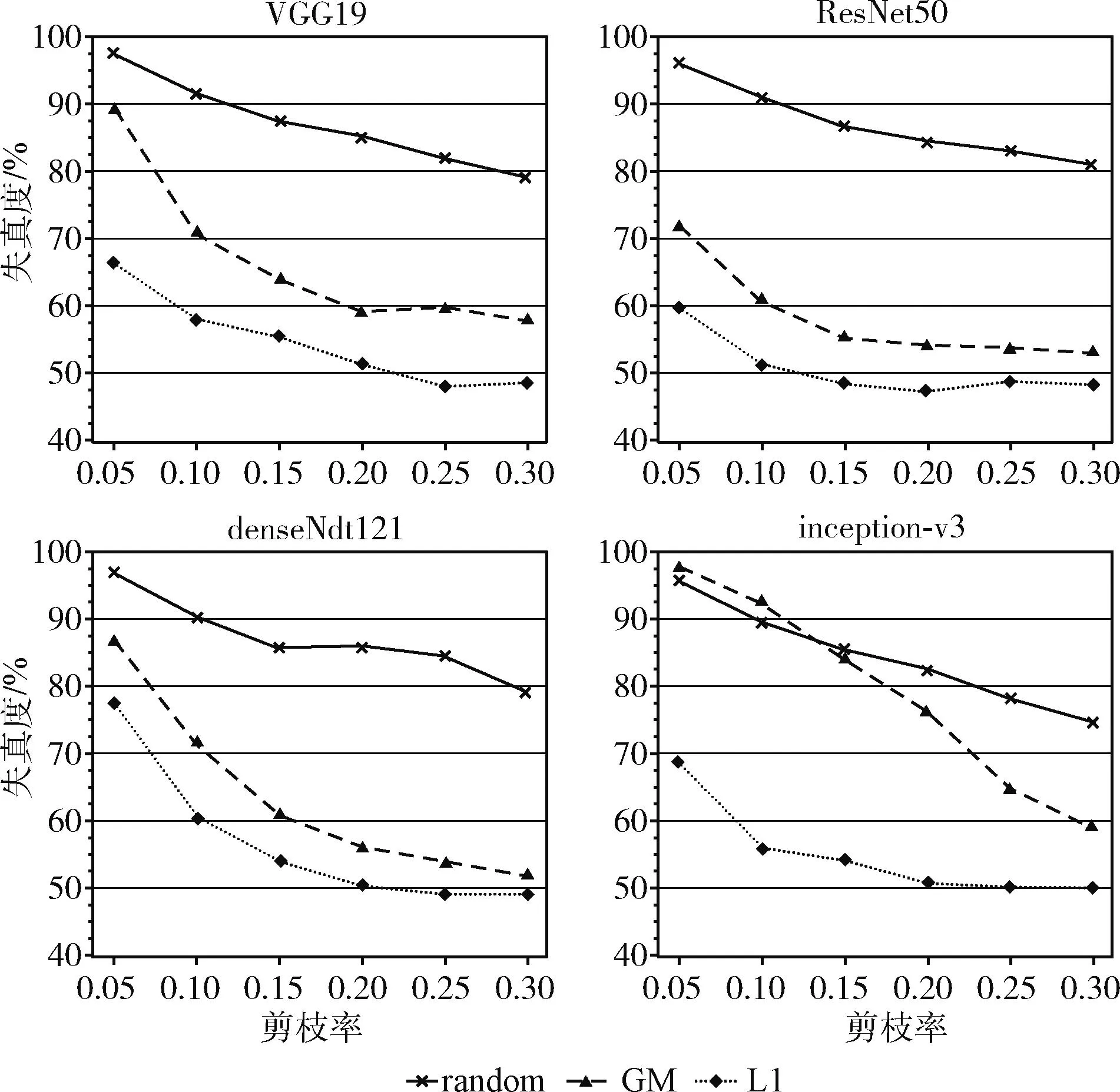
图4 多模型剪枝攻击效果对比

从图4可以看出，随着模型剪枝的强度增加，模型的失真度显著增加，使用L1范数构建参数序列，具有更高的敏感性，即使是极微小程度的剪枝率(0.05)，也能检测到模型的完整性遭受破坏，Fast-MIV可支持结构性验证，攻击者无法隐秘地改动模型结构。

实验结果表明，Fast-MIV可以支持完整性验证，且所使用的剪枝方法对比随机方法具有更好的检测性能，无论攻击者微调或删除参数，本文所提出的方法均可以有效检测出模型完整性是否遭到破坏。

4 结束语

本文提出一种基于可逆水印和模型剪枝理论的模型完整性验证算法Fast-MIV，并对比3种不同的模型剪枝方法筛选模型参数，嵌入对模型参数篡改敏感的可逆水印，可用于验证模型的完整性。本文提出了失真度指标ACCdis来衡量模型遭受篡改的程度，在多种模型上进行了充分实验。实验结果表明，所提出的算法Fast-MIV可以检测出微小的参数改动以应对剪枝或数据中毒攻击，达到保护模型完整性的效果。本文只在CNN上进行了应用和实验，下一步将研究如何将这项工作扩展到循环神经网络用于文本、语音处理的模型。