主动变径式管道机器人机构设计与性能分析

陈朋威,高飞,贾超钰

(1. 陕西工业职业技术学院 机械工程学院,陕西 咸阳 712000;2. 太原理工大学 机械与运载工程学院,山西 太原 030024)

0 引言

随着工业化和城市化的快速发展,圆形管道的应用越来越多,这类管道通常架设在空中,铺设在地下或应用于隧道中。直径小于400mm的圆形管道需要对其进行内部维护、探测等作业时,由于管道内部直径较小,人体难以进入,需要相关设备进行辅助作业。管道线路长度大于50m时,一般的探测或作业设备达不到这样的作业距离。

可移动的管道机器人作为一种有效的探测设备,可以深入人类无法到达的狭小空间内执行勘察任务[1]。国内外学者及相关公司对管道机器人理论和产品开展了大量的研究,国内轮式管道检测机器人产品较为成熟,如武汉某公司生产的多款轮式管道机器人可以实现城市地下排水管道的检测,特点是可应用于大直径管道。国外加拿大某公司开发了多款履带式管道机器人,可以应用于小直径管道,但是其产品价格高昂;韩国大邱庆北科技学院采用气动驱动研发了履带式管道机器人[2]。管道机器人理论研究方面,吴兴锋[3]研究了管道机器人避障技术;郭宪、TOURAJIZADEH H等[4-5]分别对管道机器人运动路线及控制进行了相关研究;文献[6-9]对管道机器人通过性和检测技术进行了研究;文献[10-12]对机器人结构设计和动力学特性进行了研究。

本文研制了一种应用于管道直径φ280mm～φ380mm的机器人。机器人具有主动变径机构和3组独立驱动的驱动模块,可以实现圆形管道内部影像的实时观测作业。阐述了机器人机构组成,建立了机器人在圆形管道内的位姿模型,对机器人两种典型位姿进行运动学和动力学分析,并对机器人进行了运动特性仿真;搭建了圆形管道的试验环境,对研制的机器人进行了试验研究。

1 管道机器人机构设计

管道机器人如图1所示,其机构由驱动模块、支撑结构、变径机构、CCD及光源组成。驱动模块内置伺服电机、减速机和同步带等传动机构,沿圆周方向呈120°均布,其运动可以单独控制,为机器人在圆形管道中的行走提供动力,机器人前端结构安装有CCD摄像头,可以将管道内部影像呈现在视频显示器中。

图1 机器人实物结构

变径机构如图2所示,驱动电机经联轴器驱动丝杠转动进而带动丝杠螺母及与其固定连接的零件进行直线往复运动,支承连杆通过角度的变化来调整3组驱动模块履带与管道内壁的接触压力,同时使机器人适应管道内部直径的变化。

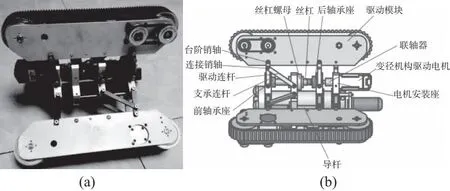
图2 机器人变径机构

2 机器人位姿和力学特性分析

2.1 机器人位姿和受力分析

定义机器人驱动模块的中心分型面与重力方向直线的夹角为β, 0°≤β≤120°,G为机器人及负载重力,N1、N2和N3为重力产生的3组驱动轮对管道内壁正压力的反作用力,由变径机构产生的驱动模块与管道内壁正压力为f,管道内机器人位姿及受力分析如图3所示。

图3 管道内机器人位姿及受力分析

机器人3组驱动模块呈120°圆周均布,当机器人3组驱动模块均与管道内壁压紧,机器人在管道中的典型位姿有两种:

1)2组驱动模块支撑重力的位姿如图4所示,此时重力G作用在下部两组驱动模块上N3=0;

图4 2组驱动模块支撑

2)1组驱动模块支撑重力的位姿如图5所示,此时重力G作用在下部1组驱动模块上N3=G;N1=N2=0。

图5 1组驱动模块支撑

当管道内顶部空间不允许受力或不允许物体通过时,机器人使用1组驱动模块支撑重力的位姿进行作业。根据力平衡条件有如下关系:

(1)

机器人沿管道内部直线运动时有如下动力学关系:

(2)

式中:F为机器人运动的总牵引力;m为机器人质量;Vt为机器人移动速度;μ为驱动模块与管道内壁之间的运动摩擦因数;Mi为驱动模块输出转矩;r为驱动轮半径。

2.2 单驱动模块支撑情况下机器人动力学及运动学分析

底部1组驱动模块支撑重力,当机器人另外2组驱动模块与管道内壁不接触时,机器人运动具有不稳定性。为研究机器人运动特性,对机器人系统进行近似处理。机器人底部驱动模块与管道内壁的接触可以看作是一个可以摆动的支点,机器人的所有质量集中于机器人的质心上,为此把变径机构和机器人系统通过适当的坐标变换转化成一个变杆长的可伸缩倒立摆模型,如图6所示。采用适当的运动控制策略后,管道机器人的运动稳定性问题可以在其运动空间中讨论。

图6 管道机器人近似模型建模

如图6所示,模型的输入包括作用于支点处的力矩τ和机器人变径力f。模型的动力学方程表示如下:

(3)

力矩τ为机器人驱动模块履带与管道内壁的滑动摩擦力产生的力矩,当管道内壁光滑时τ的数值较小,而当机器人驱动模块履带与管道内部的接触面被简化为一个点时,τ=0。在较大直径管道内运动时,为了使机器人不倒下,可以通过控制变径力f来实现机器人的摆动模式,由力学分析知:当质心处的变径力为

f=mg/cosθ

(4)

质心沿水平方向运动,这种在直观上通过改变l来保持恒定质心高度的摆就是线性倒立摆。

二维线性倒立摆的运动方程为

(5)

将式(4)带入式(5),可得:

(6)

当质心为水平运动,即y为定值时,可求得:

(7)

(8)

3 管道机器人运动特性仿真

3.1 机器人仿真试验条件

仿真试验条件:0～0.5s为管道内部放入机器人时间段,机器人4个驱动电机均不启动;0.5～3s,机器人变径电机和3个驱动模块的电机启动;3s～30s机器人在管道内部沿着管道方向运动(图7)。

图7 管道机器人虚拟样机模型

3.2 机器人在管道内运动特性仿真及分析

用多体动力学分析软件对机器人在管道内部运行特性进行运动仿真。0.5～3s阶段,机器人变径机构驱动电机速度的轨迹规划是先加速后减速,电机最大角速度270°/s。当变径机构张开到一定角度后,电机输出轴不转动,电机进入力矩保持模式,以维持变径机构的姿态,此时电机速度降为0°/s,如图8所示。

图8 变径机构驱动电机转动速度

0.5～3s变径阶段,机器人中心轨迹点OO的x轴最大值为3.2mm,机器人中心轨迹点OO的y轴最小值为-8.5mm;3～30s变径结束后机器人中心轨迹点OO的x轴数值稳定在-0.1mm;y轴数值稳定在0mm,如图9、图10所示。

图9 轨迹点x轴位移和速度

图10 轨迹点y轴位移和速度

管道长度方向z轴机器人中心轨迹点OO速度稳定在25mm/s线附近,机器人z轴位置从(3s,-1 182mm)变化到(30s,-507mm),机器人在管道内27s移动了575mm,平均速度25mm/s,说明经过变径后,机器人在管道中可以实现稳定运动如图11所示。

图11 轨迹点z轴位移和速度

仿真发现0.5～3s变径阶段,机器人中心轨迹点OO绕z轴发生旋转运动,旋转速度范围(-3.68°/s,2.68°/s),对旋转速度进行积分,得到转动角度范围为(0.78°,3.4°)。3～30s阶段,机器人中心轨迹点OO旋转速度数值为0°/s,机器人稳定运动,无转动,如图12所示。

图12 轨迹点绕z轴转动角速度

4 实验

4.1 实验条件

实验管道选用有机玻璃材料,长度3m,厚度5mm,内部直径φ320mm,管道内壁光滑。机器人质量19.8kg,机器人长度385mm,变径机构电机功率60W,变径连杆长度100mm,驱动模块电机总功率180W,最大牵引力366N,机器人实验速度100mm/s。

4.2 机器人运动特性实验

1)机器人在水平管道内摩擦条件适应性实验

实验条件:光滑管道及铺设毛毡的管道。实验研究发现在光滑有机玻璃材料管道内,机器人在启动和变径阶段发生明显打滑和自转动现象,随着驱动模块和管道内壁之间变径压力f的增大,打滑幅度和自转动幅度明显减弱,机器人在管道内稳定运行,实验数据与仿真结果基本一致,如图13和表1所示。

表1 机器人管道内部转动角度数据 单位:(°)

图13 管道不同摩擦因数的内壁机器人适应性实验

在管道内部装入毛毡垫增加管道内壁摩擦力,实验中机器人未出现明显打滑现象,机器人在管道内部可以稳定前进和后退,机器人转动角度实验数据如表1所示。

实验结果表明,通过加大管道内壁摩擦因数,机器人转动角度范围小,有利于机器人运动稳定性。

2)机器人在水平管道内姿态适应性实验

实验条件:管道在地面不固定,管道可以在地面滚转,机器人以任意姿态放入管道内。

机器人以任意姿态放入管道内,在变径机构作用下,3组履带模块与管道内壁完全接触,机器人姿态适应管道后,机器人在管道内部可以稳定前进和后退,实验结果表明机器人在管道内部姿态适应性较好,如图14所示。

图14 转动的管道内机器人运动实验

5 结语

针对圆形管道设计了可变径管道探测机器人,对机器人在管道中两种典型作业姿态进行了分析和理论建模,运用多体动力学软件对机器人在管道中的运动特性进行了仿真分析,对机器人变径阶段和稳定运行阶段的运动轨迹和数据进行了分析。搭建内径φ320mm的管道实验平台,机器人进行的摩擦条件适应性和姿态适应性实验运动特性良好,机器人运动特性的理论计算分析和实验结果基本一致,验证了机器人机构设计的合理性,表明了机器人在管道内可以稳定地开展相关作业。