轮廓几何特征融合下的电网设备激光除锈控制参数自适应确定方法
刘伟,苏文斌
(1. 贵州电网有限责任公司 电力科学研究院,贵州 贵阳 550002;2. 山东惠工电气股份有限公司,山东 淄博 255086)
0 引言
因部分环境恶劣地区的湿度过高、温度较高会使得电网设备出现严重锈蚀问题,导致输变电设备服役寿命大大减少[1-2]。同时,关键电网设备被锈蚀后,也给后续电网运行带来安全隐患。因此,对电网设备进行高效除锈已经成为电力行业亟待解决的问题。目前,激光除锈作为最常见的除锈方式,其控制参数取值直接影响了最终除锈效果。因此,众多研究人员开始针对激光除锈控制参数自适应确定方法进行研究。
文献[3] 通过有限元模型,模拟激光除锈操作过程,根据设备除锈要求选定最佳工艺参数。但是,该方法鲁棒性较差。文献[4] 提取重点工艺参数,将其看作优化变量,运用改进灰狼优化算法,建立以最优加工质量为核心的参数选取模型,再通过逼近理想解排序法进行求解,得到最优工艺参数。但是,该方法确定控制参数耗时较长。文献[5] 采用灰色关联分析方法,对正交试验数据进行分析,建立最优工艺参数优化模型。通过主效应方法,明确不同工艺参数影响下,设备表面粗糙度、应力的变化规律,从而确定最合适的控制参数。但是,应用该方法得出的控制参数进行除锈,设备表面粗糙度较高。
本文以电网设备除锈为目标,为了提升激光除锈技术的除锈效果,提出一种基于轮廓几何特征融合的除锈控制参数自适应确定方法。运用边界矩算法提取激光除锈沟槽宽度、沟槽深度、横截面积等多项轮廓几何特征,再依据融合后的特征信息进行有效控制参数选择。
1 控制参数自适应确定方法设计
1.1 构建激光除锈有限元模型
以激光解离钝化原理为核心的除锈技术,属于一种包括锈蚀层和基底的双层系统[6]。在电网设备激光除锈控制参数求取过程中,在锈蚀层、基底层交界面上选定坐标原点,向两侧引出x轴和y轴,用以描述激光束的空间分布情况,再垂直引出法线方向,最终形成图1所示锈蚀层-基底坐标。

图1 锈蚀层-基底坐标示意图
基于图1所示的坐标,建立热传导方程:
(1)
式中:a为密度;b为热容;c为热传导系数;t为时间;T为目标时间内温度分布;x为激光束的空间分布方向;z为基底和锈蚀层之间的分界面的法线方向。
电网设备激光除锈系统,只有在接收到脉冲激光后,才会出现热作用并产生热应力,实现表面锈层的去除。因此,采用ComsolMultiphysics软件,根据激光除锈工作原理构建有限元模型。在有限元模型中,设置激光照射点为热源,再通过有限元方法建立有限元网格,分析激光除锈过程中温度分布和应力分布。有限元模型建立过程中,需要在激光光束外围布置密度较小的网格,其后越靠近激光光束发射点网格密度越大,以形成可用于控制参数分析的网格模型。
1.2 提取电网设备除锈轮廓几何特征
针对电网设备进行激光除锈处理时,需要对激光扫描点进行轮廓几何特征提取[7]并将其看作控制参数确定的基础。采用基于边界矩的特征提取方法,针对实时除锈图像进行轮廓提取,再将其转换为二维数字图像函数,针对不同阶数的边界矩展开规格化处理[8],得到规格化边界矩。
(2)
式中:p、q、r表示边界中心矩的阶数;σ表示边界中心矩;λ表示规格化后的边界矩。再通过二阶规格化边界矩,生成如下所示不变矩:
(3)
式中ζ1、ζ2表示独立的不变矩。针对电网设备除锈过程,低阶数的边界矩才能更好地区分沟槽形状。所以,在电网设备除锈轮廓几何特征提取过程中,需运用式(3)所示的独立不变矩,建立新的特征矩:
(4)
式(4)计算的特征矩,不再受到比例因子的干扰。通过边界矩计算结果,可以描述除锈图像所有边界像素点的分布特征,将目标图像划分为多个扇形区域,对每一个子区域的边界矩进行修正[9],再生成子区域行向量。汇总所有行向量后,得到整幅图像的分布特征,反映激光除锈过程中沟槽的形貌。
1.3 基于特征融合的参数确定方法
为了保证电力系统的稳定运行,在电力设备除锈过程中,需要保证除锈后表面粗糙度满足要求,避免除锈操作影响设备自身功能。激光除锈本质上是通过多个光斑,按照一定路径扫描整体电网设备[10],如图2(a)所示,而单个激光点除锈处理后,得到图2(b)和图2(c)所示的沟槽形貌、沟槽搭接模式。

图2 激光扫描路径、沟槽形貌和沟槽搭接示意图
通过1.2节提出的边界矩的特征提取方法获取沟槽宽度、沟槽深度、横截面积三项主要轮廓几何特征,明确其与扫描光斑直径、激光能量密度之间存在的密切关系。所以,在参数自适应确定之前,需要根据表面粗糙度要求,定义激光扫描沟槽深度:
L=u+E
(5)
式中:L表示激光除锈单线扫描沟槽深度;u表示电网设备的锈层厚度;E表示除锈后表面粗糙度。
对于激光除锈技术来说,实际操作过程中很多控制参数的取值均会影响最终除锈质量。因此,激光除锈能量密度计算公式为
(6)
式中:R表示能量密度;ω表示峰值功率;Q表示脉冲宽度;d表示脉冲频率;F表示光斑直径;v表示激光扫描速度。
针对激光除锈沟槽轮廓,建立如下所示高斯分布几何模型:
(7)
式中:α表示沟槽轮廓上目标点与光斑中心之间的距离;I表示目标点深度值;W、Y、X表示待定常量。
根据光斑直径和能量密度,对轮廓几何特征进一步融合分析,得出沟槽轮廓的几何关系。
(8)
(9)
(10)
式中:A表示沟槽宽度;B表示沟槽深度;C表示横截面积。结合式(8)—式(10),形成沟槽轮廓数学模型,再进行列偏移量、搭接点与光斑中心距离的求解:
(11)
式中:S表示搭接点与光斑中心之间的距离;τ表示列偏移量。通过上述计算,选择激光除锈所需各项控制参数。
1.4 实现激光除锈控制参数优化
为了确保控制参数自适应确定结果满足除锈要求,结合数据统计分析方法,建立基于响应面的激光除锈控制参数优化模式。根据响应面分析原理,建立独立因子与响应值之间的响应函数:
(12)
式中:l表示考查因子;i表示独立因子;O表示独立因子总数量;k表示响应预测值;θ表示误差项;∂表示回归系数。
为了确保锈迹完全去除,通常情况下,电力设备除锈需要经历两次扫描。初次扫描需要设置最高激光能量,尽可能去除设备表面锈迹,而在第二次扫描时,需要保证电网设备的表面不受到损伤。因此,第二次扫描工艺参数的计算更需要运用上述响应函数进行优化处理。运用BOX-Benhnken Design组合,对于第二次扫描参数进行响应分析,选取响应值较高的变量,作为最优参数值。
2 实验
2.1 实验准备
为了验证文中所提除锈控制参数自适应确定方法具有可行性,选定图3(a)所示的电网设备作为实验对象。根据显微镜观察结果可知,该设备的表面覆盖了厚度不小于120μm的锈层,如图3(b)所示。此时,该电网设备锈蚀等级为B级。

图3 电网设备外观及锈层厚度
针对图3所示的实验材料,设置试验的具体过程如下:
1)在实验准备阶段,锈蚀显微图像尺寸为70×150mm,试件锈层厚度不小于120μm,每个测试位置共5幅,设置为控制点标识,对除锈图像进行轮廓提取,获取沟槽轮廓特征,生成激光扫描沟槽轮廓示意图,如图4所示,使其与能量密度之间的关联性,作为后续控制参数调整的参考。

图4 激光扫描沟槽轮廓示意图
根据图4可知,激光扫描除锈产生的沟槽轮廓,符合高斯分布模型。每个激光扫描点会出现下凹的沟槽,但在部分沟槽边缘,因为熔融锈层金属重新凝固,形成重凝颗粒物,出现凸起情况。这些凸起部分与设备表面仅有些微粘接,在后续操作时可以直接清除。
2)原材复试见证取样数必须大于等于总试验数的30%。因此,结合数据统计分析方法,确定沟槽宽度、沟槽深度、横截面积三项主要轮廓几何特征量。
3)为了更好地求取工艺参数,设置部分激光光束控制参数为固定值,设激光峰值功率为1 230 W,脉冲宽度为0.5ms,光斑直径为2.0 mm,设置激光扫描速度为15 mm/s,进行单线激光扫描。
4)展开单线激光扫描实验,经过实验操作,将控制参数自适应确定结果输入运动控制系统内,并向下方二维移动平台发送移动命令。同时,将待处理的电网设备放置于二维移动平台中心区域,随着平台同步移动,再通过供气装置连接的切割头,进行激光除锈,直至分别达到现行国家标准《GB8923—2011涂装前钢材表面锈蚀等级和除锈等级》中的Sa2.5级;表面粗糙度为30~70μm;处理后的材料表面不应有焊渣、焊疤、灰尘、油污、水和毛刺等。
5)分别设置除锈表面粗糙度为30μm、40μm、50μm、60μm、70μm,按照文中提出的参数自适应确定方法,获取最优脉冲频率和列偏移量参数。
2.2 确定最优控制参数
本文提出的参数确定方法,主要依托于轮廓几何特征融合信息。在实验过程中,首先提取沟槽轮廓几何特征,得到图5所示的沟槽几何特征随能量密度的变化曲线。
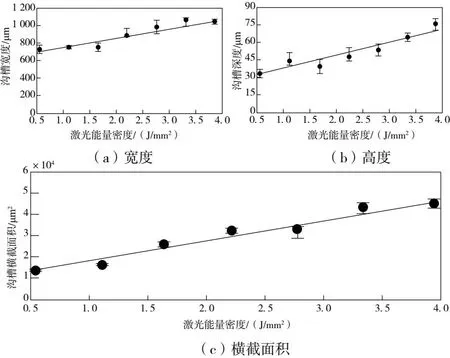
图5 沟槽几何特征与能量密度之间的关系
根据图5可知,沟槽的宽度、深度和横截面积,与激光能量密度之间均表现出线性关系。在此基础上,融合多种沟槽几何特征,进行脉冲频率和列偏移量的计算,得到表1所示的扫描控制参数计算结果。

表1 激光扫描控制参数
利用表1所示的激光除锈控制参数进行电网设备激光除锈处理,得到图6所示的除锈结果。

图6 控制参数确定后激光除锈结果
搭接扫描实验后,在体视显微镜下观察除锈后的沟槽表面和横截面状态。如图6所示,除锈试样表面呈现良好的金属光泽,扫描区域内无锈层残留,表面没有不牢固粘接颗粒,基本无过热氧化现象。
根据图6可知,确定有效的控制参数后,激光除锈技术对扫描区域完成了有效的锈层修理,呈现出具有金属光泽的除锈区,与未展开激光除锈的区域表现出极大差异。对两个区域分别进行显微镜观察,观测结果显示,经过激光除锈处理后,电网设备表面锈层基本消失,表明了所提参数确定方法的正确性。
2.3 除锈后表面粗糙度对比
选择基于响应面的参数确定方法、基于灰色关联度的参数确定方法,与本文提出方法一起进行实验。按照不同的参数求取结果,对电网设备进行除锈处理,得到除锈后表面粗糙度对比结果如图7所示。
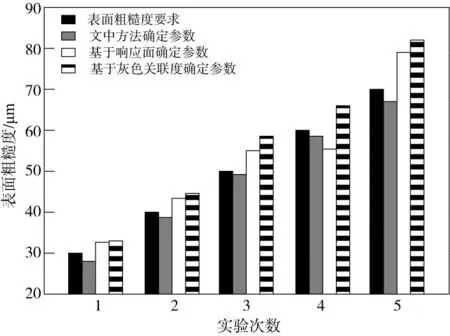
图7 不同方法除锈后表面粗糙度对比
根据图7可知,所提方法确定的控制参数应用后,除锈后表面粗糙度始终满足表面粗糙度要求,而其他两种方法大部分情况下,除锈后表面粗糙度高于要求的表面粗糙度值。整体来看,所提方法确定参数的平均除锈后表面粗糙度与要求值相比,平均偏差值为2.7μm,而其他两种方法使得除锈后表面粗糙度与目标表面粗糙度值之间偏差分别为5.9 μm、7.4 μm。综上所述,所提方法的应用可以得到更加符合除锈要求的控制参数,使得除锈后表面粗糙度偏差分别降低了54.24%、63.51%。
3 结语
针对电网设备的激光除锈工艺进行研究,提出一种依托于几何轮廓特征融合的控制参数自适应确定方法。从实验结果来看,所提方法求取的参数值可以确保除锈后表面粗糙度更加贴近表面粗糙度要求值,保证除锈操作不影响电网设备的正常工作性能。

