多工况下的直齿轮接触疲劳寿命仿真研究

潘铮,王友仁,刘维团

(南京航空航天大学 自动化学院,江苏 南京 210016)

0 引言

齿轮传动系统作为直升机主减速器、未来先进超高涵道比涡扇发动机和燃气轮机主减速器的重要部件,其需要在复杂恶劣的工作环境下长时间循环工作,可靠性要求极高。为了评估齿轮在高速重载条件下的可靠程度,需对齿轮构件疲劳损伤寿命进行研究。目前对齿轮接触疲劳寿命研究主要分为三种研究方法:基于疲劳损伤理论数值模拟计算、基于传统接触疲劳试验机的直接试验、基于有限元仿真建模的寿命预测。文献[1]在弹流润滑条件下进行应力分析,通过Matake准则与DangVan准则对比进行齿轮接触疲劳寿命分析。文献[2]在考虑表面粗糙度对次表面应力场特征的影响下,基于最大主应力准则和临界平面法建立齿轮多轴疲劳寿命模型。文献[3]基于分形理论细化齿面表面粗糙度分布,通过Sines模型建立多轴疲劳预估模型并进行等效滚子摩擦试验进行验证。文献[4]通过真实形貌实测齿面表面粗糙度,预估齿面损伤产生深度,通过预设损伤预估SWT模型的齿面损伤萌生扩展寿命。文献[5]提出基于Fatemi-Socie损伤萌生准则结合多轴疲劳计算的数学模型,并与有限元仿真分析结果进行对比验证。文献[6]对简化齿轮模型进行静力学和瞬态动力学有限元分析,通过瞬态动力学分析结果编制时间序列载荷谱,并对传动齿轮疲劳寿命进行预测。文献[7]通过Workbench分别在静载条件下建立简易载荷谱和动载条件下简化模型,获得部分载荷谱,建立静载和动载条件下的疲劳寿命分析模型。文献[8]通过接触疲劳试验机进行齿轮接触疲劳试验,拟合齿轮接触疲劳寿命曲线。文献[9]基于混合弹流润滑理论、连续力学损伤理论和Archard磨损定律,开发了一种结合滚动接触疲劳和磨损影响的数值疲劳寿命模型,并使用三接触台进行试验与对比验证。

从近年来的研究现状来看,传统接触疲劳试验数据可靠性高,可用于拟合经验模型,但是其本身试验周期过于冗长、航空材料齿轮也较难以获得,对于航发及燃气轮机所用的齿轮传动系统进行相关测试耗费资源过于巨大。数值模拟计算在计算效率方面具有独特的优势,准确度也较高,然而其多数依据二维平面进行建模,难以考虑齿宽方向、三维平面的接触疲劳变化情况,对于齿轮疲劳损伤区域的预测缺乏直观的解释与说明。因此,通过有限元分析软件进行接触疲劳寿命分析成为目前工程应用与科学研究的重点手段之一。但在目前的仿真分析接触疲劳寿命的研究中,循环载荷谱编制不准确,缺乏对齿轮工作环境变量、齿轮齿面边界条件的考量,也并没有与数值模拟相关成果进行结合。综上所述,本文使用Ansys Workbench和nCode进行有限元分析,通过赫兹接触压力校核有限元仿真结果,结合考虑齿面表面粗糙度的弹流润滑摩擦因数,基于全尺寸齿轮编制时间子步载荷谱,建立直齿轮接触疲劳模型,研究多工况、表面完整性等因素对接触疲劳的影响,为后续接触疲劳、点蚀形貌试验方案与材料选用探明方向。

1 直齿轮啮合过程分析

1.1 直齿轮基本参数

所采用的某接触疲劳试验机的直齿轮参数如表1所示。

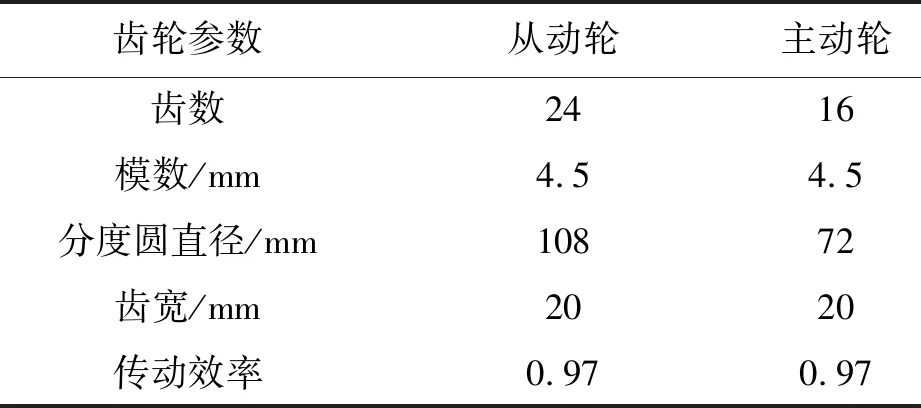
表1 齿轮基本参数

1.2 齿面接触强度

在齿面接触疲劳强度校核中主要使用赫兹接触应力作为主要应力进行计算,如图1所示。

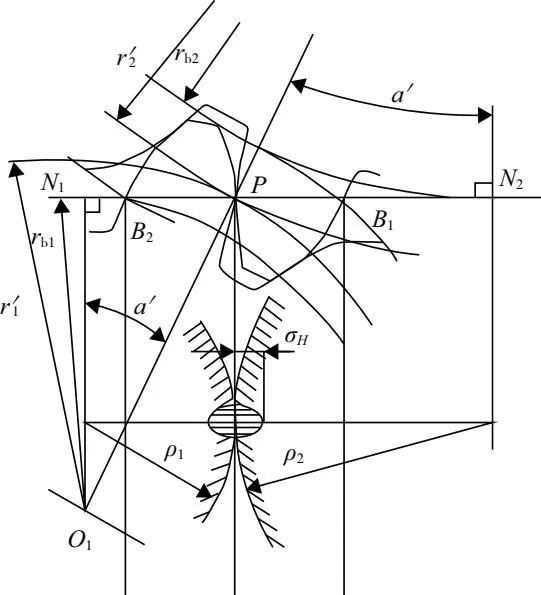
图1 赫兹接触应力

实验[10]表明,齿根部分靠近节线处最易发生点蚀,故取节点P处接触应力作为齿面接触应力计算依据,经过简化处理的齿面接触强度计算公式如下:

(1)

1.3 考虑齿面表面粗糙度的齿面摩擦因数

根据文献[11]中大量实验得到的弹流润滑状态下的时变摩擦因数公式,在齿面表面粗糙度为0.2μm、0.4μm、0.6μm情况下,计算得到的齿面摩擦因数如图2所示。通过计算摩擦因数的方均根值得到对应的摩擦因数分别为0.014、0.021、0.042。

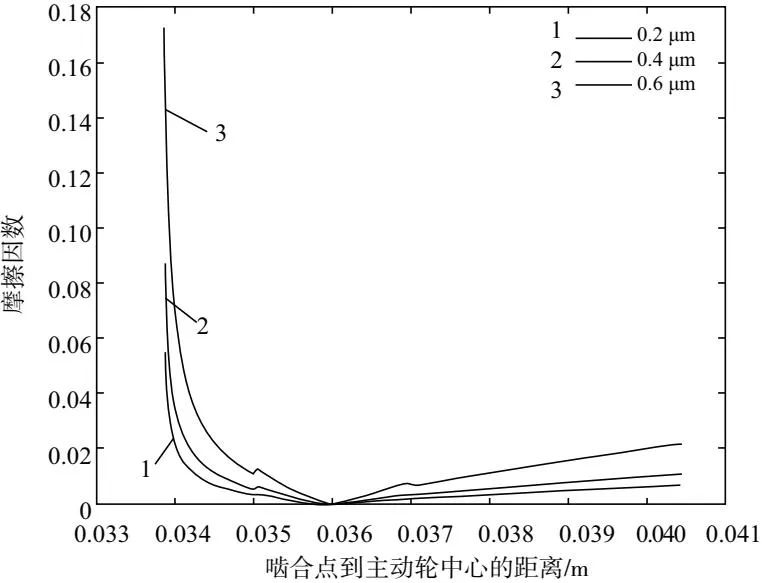
图2 不同齿面表面粗糙度的齿面摩擦因数

2 直齿轮接触疲劳有限元仿真模型建立

2.1 直齿轮静力学分析模型

根据表1相关参数进行齿轮建模,在Hypermesh中划分轮齿接触模型,采用六面体单元进行网格划分,主动轮单齿模型节点239 646个,单元215 700个,主动轮基圆单齿模型节点4 900个,单元4 000个,旋转复制按照齿数角度关系(θ=360/z1),保证计算接触应力的准确性,如图3所示。

图3 轮齿接触模型网格划分

根据齿轮啮合输入输出关系,若负载转矩30 000Nmm则主动轮输入转矩为20 619Nmm,使用joint-revolute来设置主动轮单自由度旋转副,joint-fixed设置从动轮为固定旋转副。

通过Workbench求解,最后得到相应负载转矩设置的接触应力结果,如图4所示。

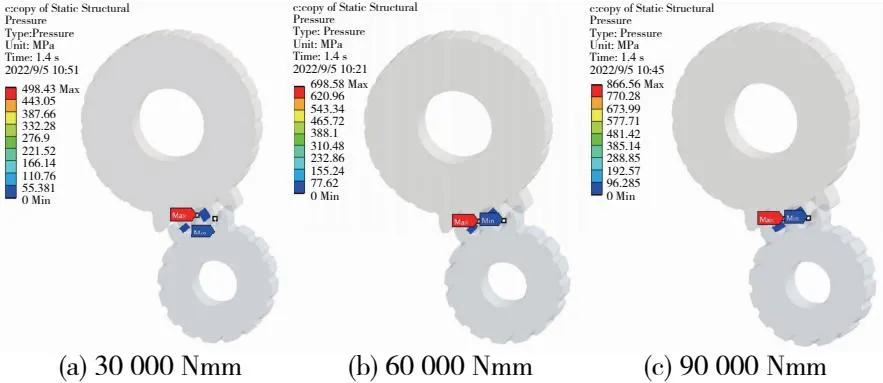
图4 静力学应力云图

通过理论解校核有限元解,根据表2可知,仿真计算与理论解误差在5%以内,并且基本高于理论解,故认为仿真结果相对可靠,可以进行较为保守的寿命预测。

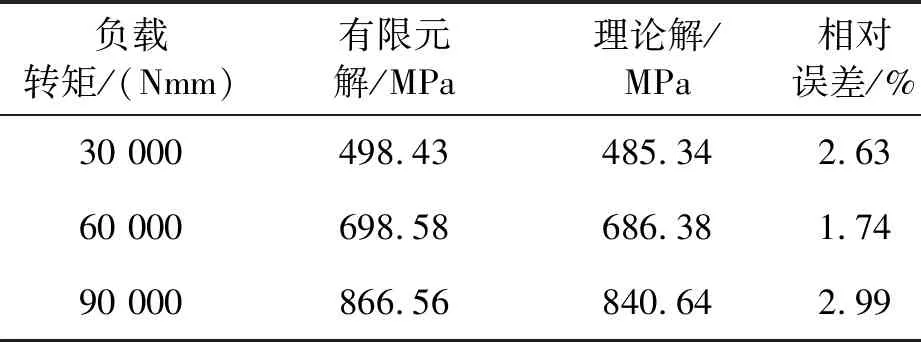
表2 有限元结果校核

2.2 直齿轮瞬态动力学分析模型

根据表1进行齿轮建模,为得到精确的应力时间子步历程,需建立全尺寸模型。在Hypermesh中进行网格划分,考虑计算资源使用率和计算效率,需对整体网格数量进行控制,整体齿轮模型节点103 840个,单元86 080个,如图5所示。

图5 全齿模型网格划分

使用joint-revolute设置主动轮转速,使用joint-moment设置从动轮负载转矩,在contact中根据1.3中计算出的齿面摩擦因数方均根值进行设置。

2.3 时间子步载荷谱编制

疲劳分析中所使用的疲劳评估应力时间子步载荷谱定义如下:

S(step)=P(step)×ScaleFactor×SFE

(2)

式中:S(step)为时间子步历程应力;SFE为有限元求解应力;P(step)时间子步载荷通道的载荷乘子,ScaleFactor为用户自定义载荷放缩系数。

目前，操作模式优化相关概念在很多学科中被广泛提出并应用。桂卫华等[1]在铜闪速熔炼领域定义了操作模式优化的相关概念，提出了一种操作模式优化的方法。复杂工业过程的数据主要包括：输入条件、状态参数、操作参数以及工艺指标[3- 4]，对于纸浆洗涤过程，数据可描述如下。

2.4 材料S-N曲线

对某型航空齿轮所用材料进行仿真分析,该材料为Cr合金锻钢,其抗拉强度为1 010MPa。由于该材料在nCode材料库中并不存在,需使用具有UTS修正的S-N曲线方法进行保守估算,其S-N曲线如图6所示。

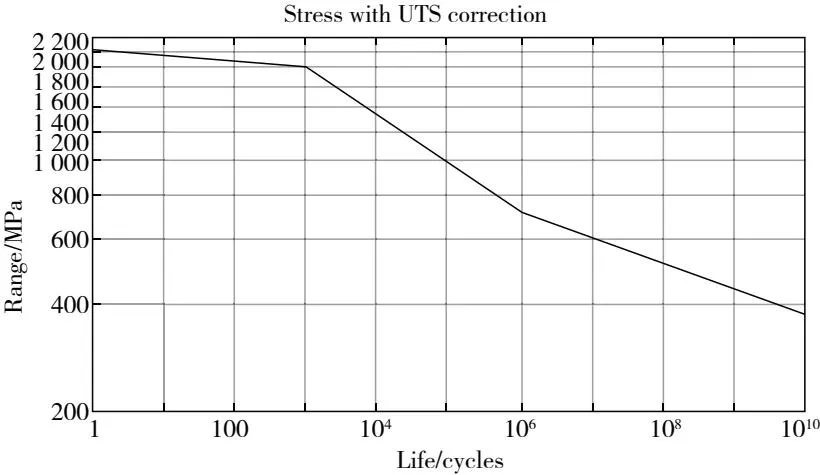
图6 材料S-N曲线估计

2.5 齿面接触疲劳寿命预测模型

通过Ansys Workbench齿轮传动静力学分析研究齿轮稳定啮合传动时齿轮啮合区域的应力-应变特征,基于齿轮瞬态动力学加载循坏载荷下的载荷变化情况并对比确定载荷放缩系数,在ncode的SN疲劳(应力疲劳)模块下,使用临界平面法与雨流计数法计算应力范围与平均应力并结合Goodman等寿命平均应力修正,最后应用Palmgren-Miner线性损伤累积理论进行接触疲劳寿命预测,得到失效萌生的循环次数与齿面区域,如图7所示。

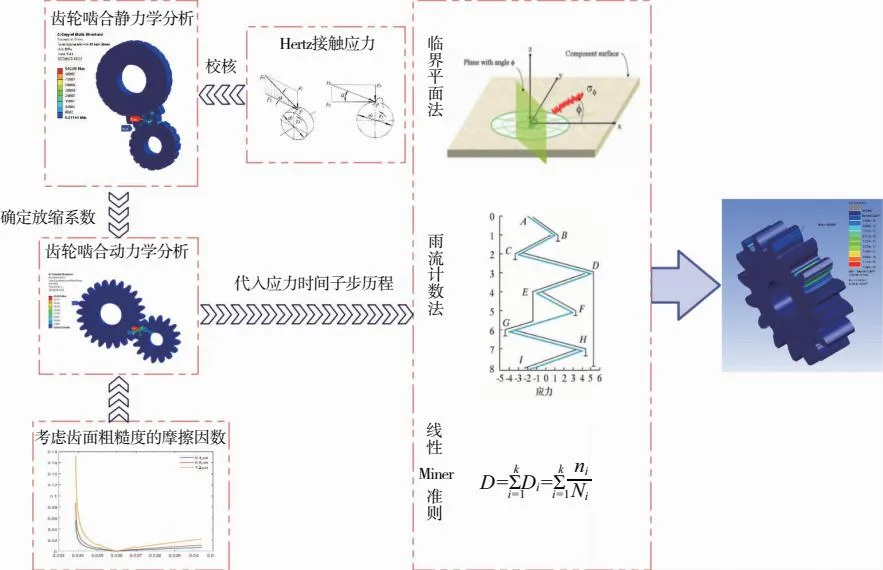
图7 齿面接触疲劳寿命预测流程

3 仿真结果及分析

3.1 不同输入转速下的接触疲劳寿命分析

分别设置1 200r/min、1 500r/min、1 800r/min的主动轮转速和30 000Nmm的从动轮负载转矩进行瞬态动力学分析,得到齿轮应力-时间子步历程,再叠加与负载转矩30 000Nmm的静力学分析结果对比,得到放缩系数,进行接触疲劳寿命计算,得到1 200r/min、1 500r/min、1 800r/min下的疲劳寿命云图,以分析主动轮为主,如图8所示。

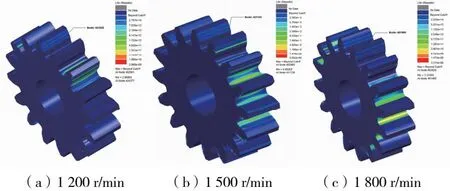
图8 不同输入转速下主动轮接触疲劳分布

在应力历程输入时,1 200r/min工况根据其周期与时间的关系只代入一个整周期0.05s,而1 500r/min与1 800r/min代入两个整周期分别为0.08s和0.066 7s,因此循环次数在1 500r/min和1 800r/min的分析中需进行转换,分别为1.37×109次和6.63×108次,其工作寿命和危险节点如表3所示。

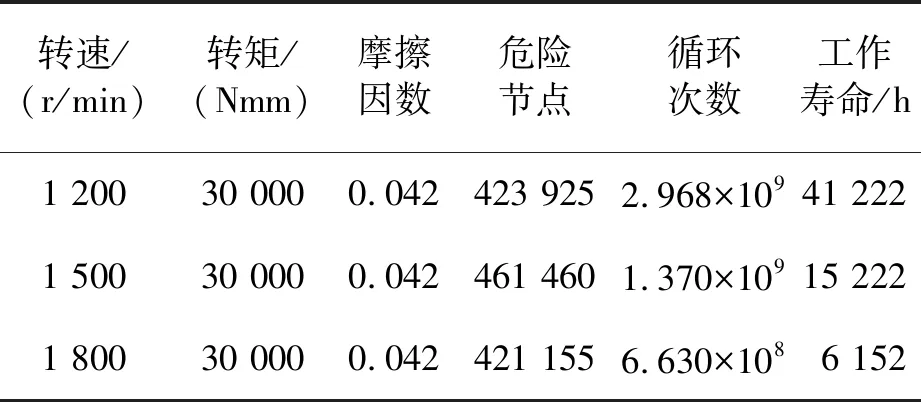
表3 不同转速主动轮接触疲劳寿命分析结果

根据表3可知,在相同负载转矩下,转速与循环次数呈负相关,这是由于转速增大齿轮应力历程波动增加,对应损伤累积过程更加迅速。同时,转速越大其工作寿命越短,这是由于转速越大齿轮经历一个循环应力整周期的时间就越短。从分析结果中可以看出,危险节点大多出现在齿面节线两端位置,在同一齿宽方向上,两端边缘位置所受应力大于中心位置。

3.2 不同负载转矩下的接触疲劳寿命分析

设置相同转速2 100r/min下负载转矩分别为30 000Nmm、60 000Nmm、90 000Nmm,进行瞬态动力学分析,并叠加各自的静力学对比,生成的放缩系数,得到不同负载转矩下的疲劳寿命云图,以主动轮为主,如图9所示。其工作寿命和危险节点如表4所示。

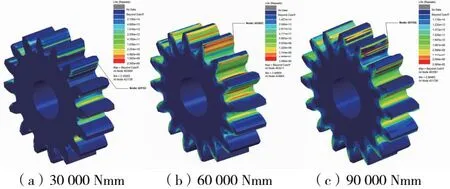
图9 不同负载转矩下主动轮接触疲劳分布

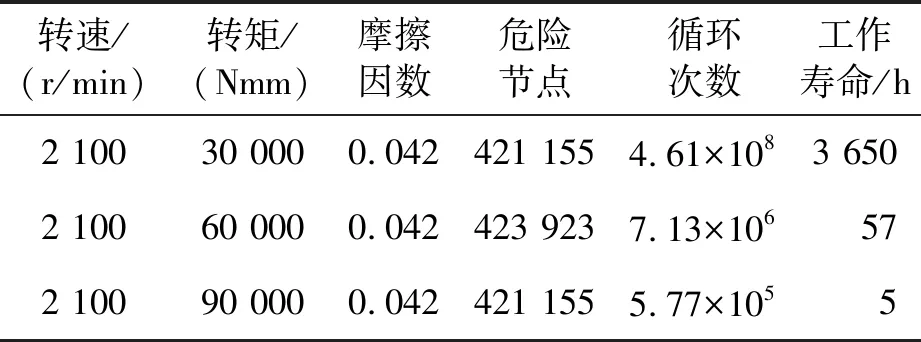
表4 不同转矩主动轮接触疲劳寿命分析结果

根据表4可知,负载转矩越大齿轮循环次数越小,这是由于负载转矩增大使输入转矩增大,接触应力也将增大。与3.1分析结果对比可以看出:1)负载转矩对接触疲劳寿命的影响幅度远高于输入转速;2)对于航空齿轮的实际使用来说,若想保证在高速重载情况下维持较高工作寿命,需更换屈服强度更大的材料。

3.3 不同摩擦因数下的接触疲劳寿命分析

进行相同转速1 200r/min相同负载转矩30 000Nmm的齿轮瞬态动力学分析,设置不同齿面表面粗糙度0.2μm、0.4μm、0.6μm影响下的摩擦因数进行齿轮静力学分析,得到相应的载荷放缩系数,得到不同齿面表面粗糙度下的疲劳寿命云图,以主动轮为主,如图10所示。

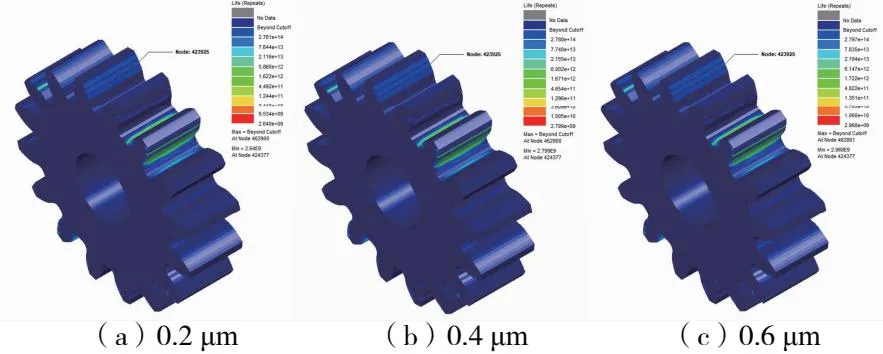
图10 不同齿面表面粗糙度下主动轮接触疲劳分布

根据表5可知,摩擦因数与接触疲劳呈正相关,这是由于在弹流润滑状况下齿面的摩擦因数越小表明齿面之间的油膜厚度越大,过大的油膜厚度也会导致齿面间润滑油的浓稠度上升,齿面接触压力增大,这与文献[12]的推论相一致。从分析结果可以得出,齿面摩擦因数对工作寿命的影响幅度较小,在弹流润滑状态下齿轮的工作寿命相对较高。

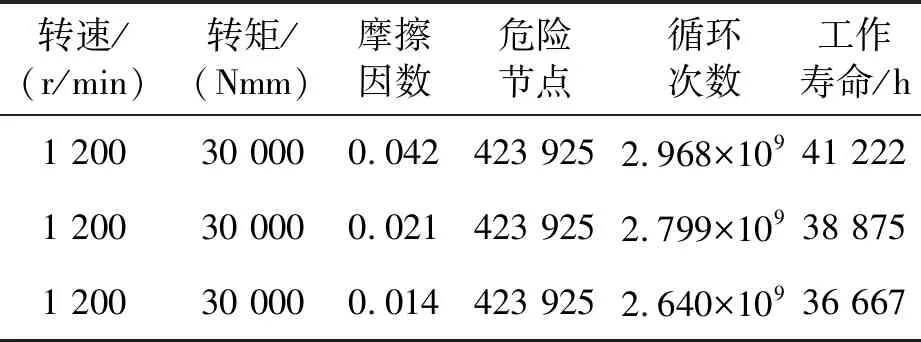
表5 不同摩擦因数主动轮接触疲劳分析结果

4 结语

1)建立齿轮接触疲劳寿命仿真模型,得到不同输入转速、负载转矩、摩擦因数下的接触疲劳寿命和最易发生损伤的危险节点。

2)得到3种影响因素对齿面接触疲劳寿命的影响规律与影响幅度。通过危险节点位置的预测,得到齿轮沿齿宽方向的两端较中间位置更易出现损伤。仿真实验数据可以为齿轮接触强度评估和后续疲劳试验提供参考。