工业机器人用盘式永磁电机设计与优化
李晨
(大连交通大学 机械工程学院,辽宁 大连 116028)
0 引言
工业机器人已经广泛应用于机械加工、电子电器、物流等行业[1],电机作为其核心零部件对整个工业机器人的稳定运行起着关键作用[2]。其中径向磁通永磁电机由于其设计技术比较成熟得到了广泛的应用[3-5]。但是其轴向尺寸大,导致电机在机器人的质量及体积占比大。为解决上述问题,文献[6] 提出了一种适用于机器人关节驱动系统的盘式电机,在相同的尺寸下可以达到更高的输出功率和输出转矩。
双定子单转子结构是盘式电机的一种基本结构,由于双定子是对称的,所以转子受到两个相互抵消的磁拉力,提升了电机的机械稳定性[7-9]。而双转子单定子电机由于存在两个转子,所以其转动惯量较大,故本文结构采用双定子单转子结构。
目前主流厂商生产的工业机器人搭配的永磁同步交流伺服电机主要是表贴式永磁同步电机[10],而内置式永磁电机存在磁阻转矩,和表贴式永磁电机相比,电机调速能力与过载能力得到了进一步的提升[11-12]。基于此,本文提出一种内置式盘式永磁电机;相较于表贴式盘式永磁电机输出转矩得到了提升,带负载能力得以加强。
本文基于法拉第电磁感应定律及永磁电机运行原理,推导出盘式电机转矩的公式;同时对内置式盘式永磁电机的空载反电动势、气隙磁密、齿槽转矩进行了有限元仿真分析,对气隙的大小、永磁体内径进行了优化和分析。
1 内置式盘式永磁电机参数的选取及转矩的计算
1.1 盘式永磁电机转矩的计算
法拉第电磁感应定律为
(1)
式中:B为磁感应强度;ω为电机轴旋转的角速度;L为导体切割磁感线的有效长度。
对于盘式电机来说,切割磁感线的导体为沿着半径方向的导线,其余的部分未参与切割磁感线,所以只有这部分的导体产生感应电动势:
(2)
式中:θ为角度;Dmo为定子外径;Dmi为定子内径。
定义气隙磁密平均值为Bav,则每根导体产生的平均电动势为
(3)
若电机的线圈匝数为N,分布系数为kd,短距系数为ky,每相并联支路数为a,则电枢电动势
(4)
可以求出电机功率
(5)
则电磁转矩
(6)
由于本电机为双定子单转子盘式永磁电机,其电磁转矩为
(7)
1.2 电机定子内外径的选取
根据电磁转矩公式,定子的内径和外径的尺寸大小决定着盘式永磁电机输出转矩大小,首先对定子的内径和外径进行设计。根据文献[7] 可知,盘式永磁电动机的主要尺寸比为
(8)
式中:Lef为电枢绕组导体的有效长度,Lef=(Dmo-Dmi)/2;Dav为电枢的平均直径,Dav=(Dmo+Dmi/2);γ为永磁电机磁极的外径与内径之比,γ=Dmo/Dmi。
需设计一台工业机器人用盘式永磁电机,根据设计要求确定定子外径Dmo=200mm,在综合考虑用铜量、效率、电负荷、漏磁等因素,将定子内径Dmi设置为135mm。
1.3 电机极槽配合设计
为了设计电机的极数和槽数,本文对下列5种18/8、18/10、18/12、24/8、24/12极槽配合下的永磁电机进行有限元仿真计算,得到不同极槽配合下的永磁电机输出转矩大小,如表1所示。

表1 不同极槽配合下的永磁电机输出转矩
根据表1可以看出,18/12这种极槽配合形式的永磁电机输出转矩的最大,但转矩的波动比较大,而18/10极槽配合形式虽然比18/12极槽配合形式的永磁电机输出转矩低14.6%,但波动情况大幅度降低。基于此,本文选用18/10这种极槽配合形式的永磁电机。
1.4 模型的建立与参数的选取
双定子单转子电机是由2个定子、1个转子组成,2个定子位于中间转子的左右两侧,在定子和转子之间存在一定的空隙,本文初始值将其设置为0.8mm。在Ansys maxwell软件里建立盘式永磁电机的三维有限元模型,如图1所示。
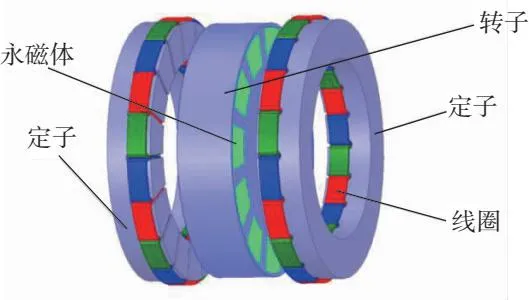
图1 内置式盘式永磁电机结构
经过上面的设计,得到了内置式盘式永磁电机结构参数的初始值,如表2所示。
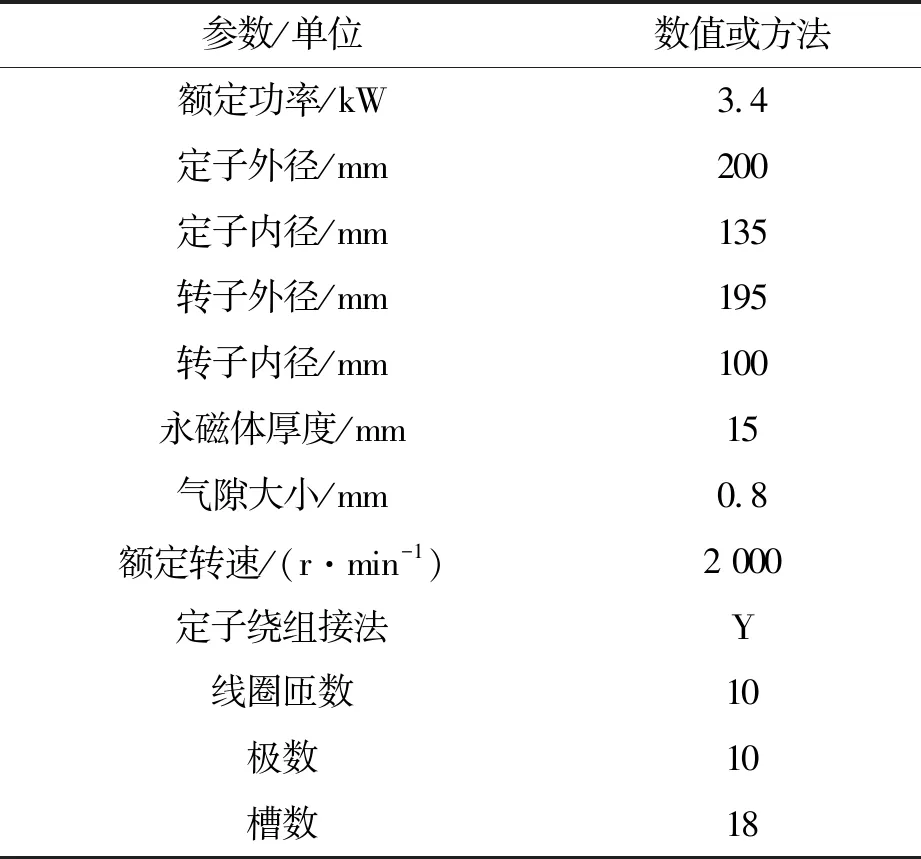
表2 内置式盘式永磁电机初始结构关键数据
2 内置式盘式永磁电机电磁性能仿真与分析
2.1 内置式盘式永磁电机和表贴式盘式永磁电机输出转矩对比
为对比内置式盘式永磁电机和表贴式盘式永磁电机的输出转矩,利用有限元软件对两种不同类型的电机在一个周期内进行仿真,仿真结果如图2所示。
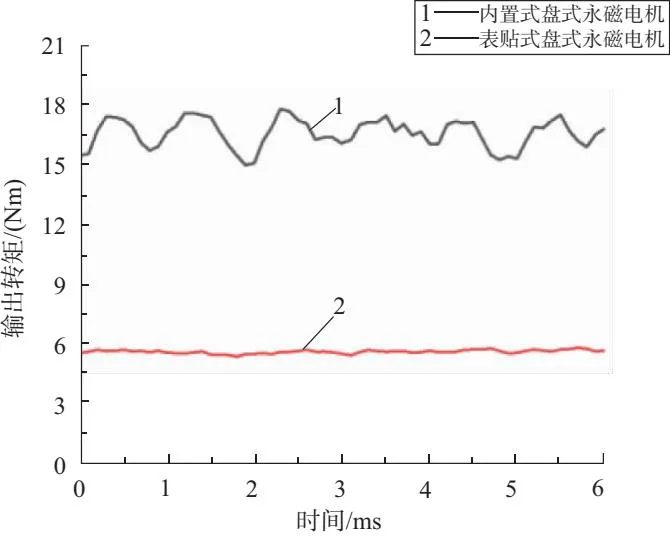
图2 两种盘式永磁电机对比分析
表贴式盘式永磁电机输出的结果比较稳定,但输出转矩只有5.6Nm左右,而内置式永磁电机虽然输出转矩波动略大,但输出转矩的平均值在16.5Nm,要明显高于表贴式盘式永磁电机。对于输出转矩稳定性的要求并没有那么高,而输出转矩的大小要求较高的搬运机器人,应用内置式盘式永磁电机是较为合适的。
2.2 内置式盘式永磁电机空载气隙磁密分布
为了描述永磁电机的漏磁情况,在气隙靠近定子和转子0.1mm处,在不同的半径位置观察其磁感应强度大小,如表3所示。
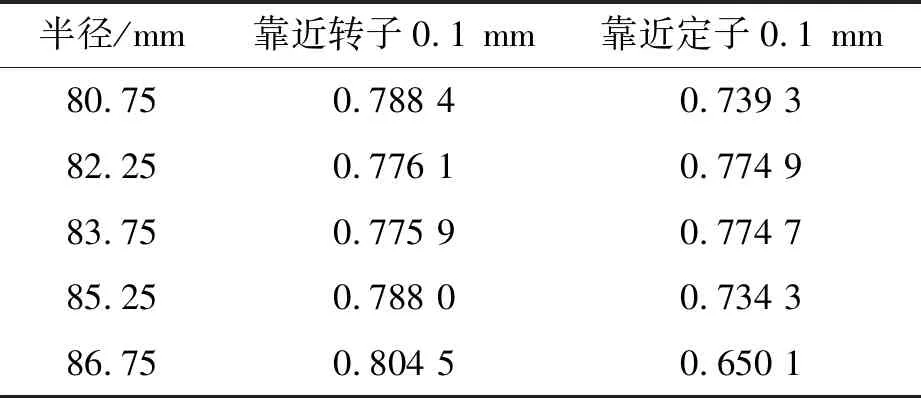
表3 不同位置磁感应强度的平均值 单位:T
由于永磁体在转子上面,所以靠近转子部分的磁感应强度较高,这说明在气隙部分处会发生漏磁现象,但通过上述结果来看,虽然有漏磁现象的发生,但漏磁并不大。以半径为85.25mm、靠近转子0.1mm处为例,观察其圆周的气隙磁密分布情况,如图3所示。
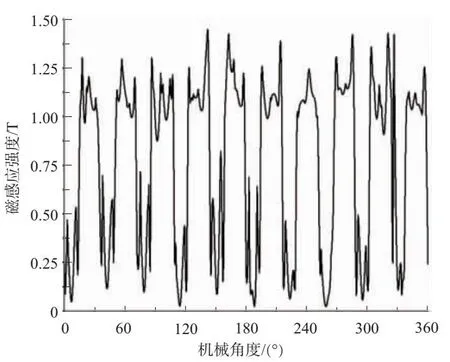
图3 气隙磁密分布图
根据仿真结果,气隙磁场的最大值为1.448 1 T,平均值是0.775 9 T,靠近转子的位置距离永磁体较近,磁感应强度较大;而在1个周期之内出现了10个波峰和10个波谷,这主要是因为电机的极数是10极,设计是合理的。
2.3 内置式盘式永磁电机空载反电动势
谐波畸变率是描述电机空载反电动势稳定运行的标准之一,数值越小,运行越稳定。为了计算谐波畸变率,对内置式盘式永磁电机进行空载状态下的有限元仿真,仿真时需要将电流激励设置为0,这样就可以得到只有永磁体作用下永磁电机的特性。为了方便计算,仿真结果只保留第一个周期,如图4所示。

图4 空载反电动势
根据有限元的仿真结果,空载反电动势的峰值为55.19 V;同时可以看到空载反电动势的曲线并不是标准的正弦曲线,存在着一定的谐波,这主要是由于存在着齿槽转矩。为了更好地计算永磁电机的谐波畸变率,对空载反电动势进行傅里叶分解(图5),由于高次谐波的数值太小,所以在图里只保留前20次谐波。
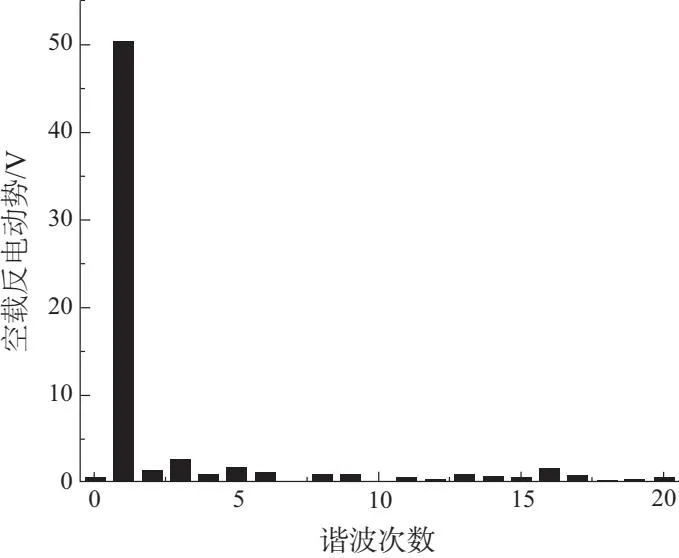
图5 空载反电动势各次谐波
基波有效值为50.26 V,总有效值为68.85 V,计算得到空载反电动势谐波畸变率为6.64%,空载反电动势谐波畸变率数值较小,说明运行稳定。
2.4 内置式盘式永磁电机齿槽转矩分析
齿槽转矩过大会引起噪声和振动,造成电动势的正弦度低等问题,图6为电机在1个周期内的齿槽转矩大小。

图6 内置式盘式永磁电机的齿槽转矩图
3 内置式盘式永磁电机结构优化
由于内置式盘式永磁电机的输出转矩较大,但波动较大,所以下面从气隙大小和永磁体内径对电机的波动情况和输出转矩大小进行优化设计。
3.1 气隙大小对内置式盘式永磁电机的影响
气隙大小影响着磁场的强弱,进而影响永磁电机输出转矩的大小,选取不同的气隙大小分别进行有限元仿真。
如图7所示,随着气隙的逐渐增大,电机的输出转矩在逐渐减小;在气隙为0.5mm时输出转矩最大,但转矩的波动也很大。因为工业机器人的运行转矩波动越小越好。所以经过对比分析,永磁电机的气隙大小设置为0.6mm。

图7 气隙对输出转矩的影响
如果气隙设置为0.6mm,永磁电机的齿槽转矩的幅值变为0.1Nm(图8),相较于之前的0.8mm时,齿槽转矩有了一个下降,从而也可以看出,在气隙大小为0.6mm比0.8mm时,运行更加稳定。
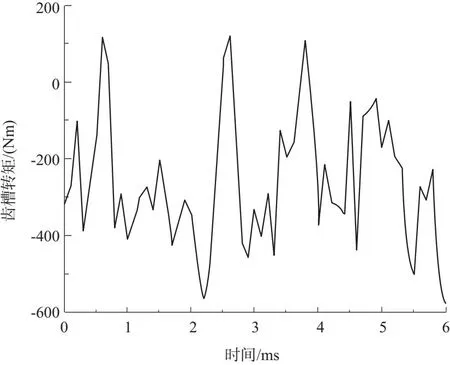
图8 0.6mm时的齿槽转矩图
3.2 永磁体内径对内置式盘式永磁电机的影响
永磁体是磁场产生的主要来源,在永磁体外径确定的情况下,选取不同的永磁体内径大小分别进行有限元仿真。
如图9所示,随着永磁体内径的增加,永磁体输出转矩基本上呈现减小的趋势,这是由于在永磁体外径不变的情况下,内径逐渐增大,永磁体的体积在逐渐减小,进而导致永磁体所产生的磁场减小,而输出转矩受磁场大小的影响,从而导致输出转矩也有了减小。在永磁体内径为146mm时,永磁体的输出转矩取得极值,而波动大小也仅为0.15,适合电机在工业机器人上的运行,所以将永磁体内径设为146mm。
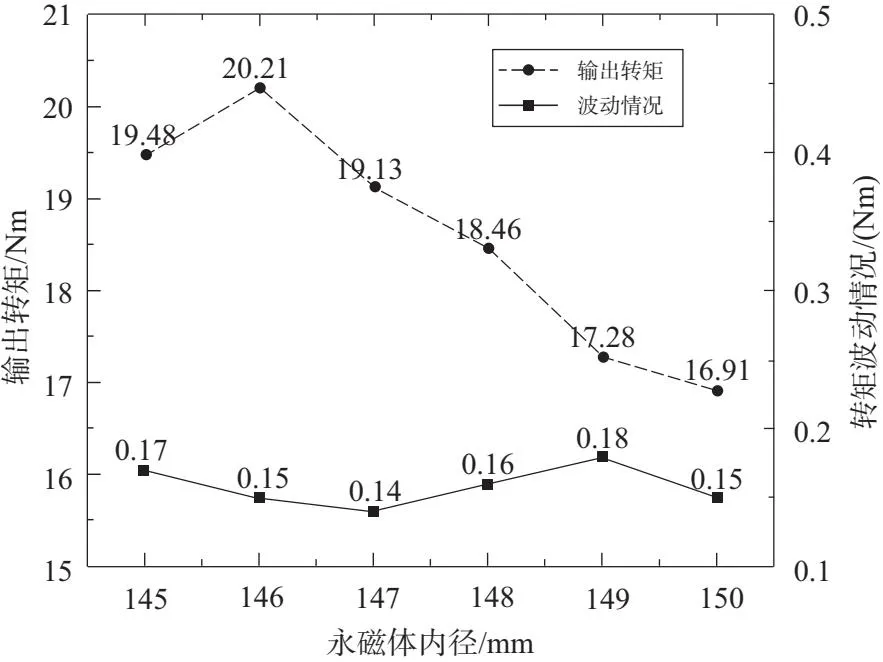
图9 永磁体内径对输出转矩的影响
3.3 优化前后输出转矩对比分析
本文主要对气隙大小和永磁体内径进行了优化,得到了内置式盘式永磁电机优化前后的输出转矩和齿槽转矩,如表4所示。

表4 内置式永磁电机优化前后对比
4 结语
本文建立了内置式盘式永磁电机的三维模型,推导出盘式永磁电机的转矩大小,通过与表贴式永磁电机输出转矩进行对比,内置式永磁电机输出转矩得到了提升;为了验证内置式盘式永磁电机运行的可行性,对其空载反电动势、气隙磁密、齿槽转矩进行仿真与分析;通过对电机的气隙大小及永磁体内径的优化,输出转矩得到了22.5%的提升。

