基于LMI和扰动观测器的电动伺服系统RBF神经网络控制

李晓飞,范元勋,许鹿辉

(南京理工大学 机械工程学院,江苏 南京 210094)

0 引言

电动伺服系统又称电动直线负载模拟系统(ELLS),是对某型号航天用直线舵机进行硬件在环仿真的一种试验装置,可实现在一定精度范围内对直线舵机的动态加载。但由于系统本身存在的不确定性和舵机位置输入所产生的多余力干扰,使得ELLS在实际加载的过程中很难实现对输入信号的实时动态跟踪[1]。因此,实现对系统的精准控制,提高加载过程中的准确度,是ELLS的重点研究内容。

目前,众多学者通过不同的控制理论对类似系统进行准确的跟踪控制,主要有滑模控制、自抗扰控制、模型自适应控制及模糊和神经网络自适应等控制方式。针对控制系统中存在的非线性问题,LIU等[2]提出了一种基于神经网络近似的反演滑模控制方法并利用神经网络逼近器来在线估计航天器的动力学不确定性,有效地减少了滑模控制的抖振。聂守成等[3]利用干扰观测器估计模型的不确定性并将其引入滑模切换函数中,结合自适应算法完成对系统的位置跟踪。对于未知的负载转矩扰动,董中华等[4]针对采摘机械臂的不确定性设计一种PSO-RBF神经网络自适应控制器,有效地实现轨迹的跟踪。

在具有反馈环节的控制系统设计过程中,需经常考虑系统中存在的不确定性等约束条件,在处理这些问题时,其中一种思路就是将其转换为一个带有LMI约束的最优化问题[5]。孙宜标等[6]将通过扩张观测器与LMI滑模控制结合,应用到直线伺服系统中,提高了系统的鲁棒性。

为了提高系统的跟踪精度,本文在建立系统状态空间表达式和跟踪目标模型的基础上,基于LMI理论设计扰动观测器并将其应用到RBF神经网络控制器中,结合仿真验证该方法的有效性。

1 系统组成及其数学模型

1.1 结构组成

根据系统的功能划分,ELLS可分为加载系统、舵系统和测控系统3个组成部分,结构组成如图1所示。加载系统由PMSM、滚珠丝杠副及其之间的连接单元组成;舵系统由被测直线舵机组成;测控系统由上位机、工控机和数据采集单元组成。舵机被加载系统通过拉压力传感器与加载系统机械连接,以此完成对舵机的动态加载。由上位机编写PMSM和舵机运动控制程序,经TCP/IP传送至工控机,随后分别通过EtherCAT协议和RS422通信将控制指令传送至PMSM和舵机,与此同时,工控机对上位机传送过来的数据与采集卡接收的各传感器数据进行实时比较,形成闭环控制。

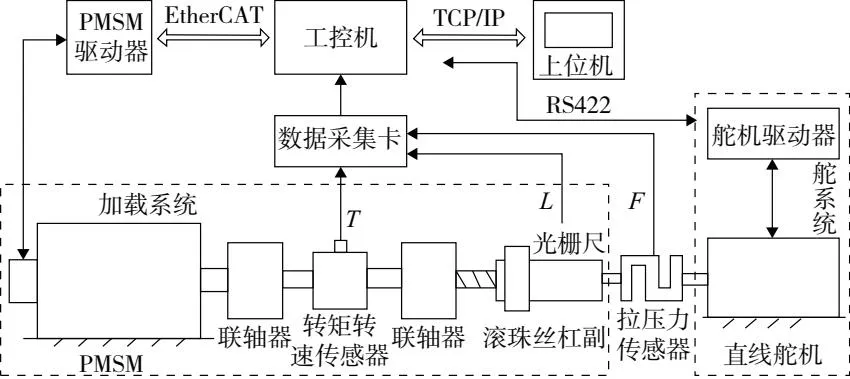
图1 ELLS结构组成示意图

1.2 数学模型

ELLS的数学模型主要从PMSM和中间传功环节的分析得到。采用d-q坐标转换对PMSM进行建模。对其进行简化,令d轴id=0,得到定子电压和电磁转矩方程,这里直接给出动态方程[7],如式(1)所示。

(1)

式中:Lm、uq和iq分别为q轴的等效电感、定子电压和电流;Rm为定子电阻值;ωe为转子电角速度;Ke为反电动系数,且Ke=Lmid+ψf,其中ψf为转子永磁体磁链,id为d轴的等效定子电流;Kt为转矩系数,且Kt=pnψf,其中pn为极对数;TL、Jm分别为折合到转轴上的负载转矩、等效转动惯量;Bm为阻尼系数;ωr为机械角速度。

视转矩转速传感器为弹性元器件,结合滚珠丝杠的运动转换关系,得到两者的数学模型如式(2)所示。

(2)

式中:KA、θr、θl分别为转矩转速传感器的刚度系数和输入、输出角位移;η和P分别为滚珠丝杠副的传动效率和导程。

综合式(1)和式(2),经拉普拉斯变换,得到图2所示的ELLS的模型。

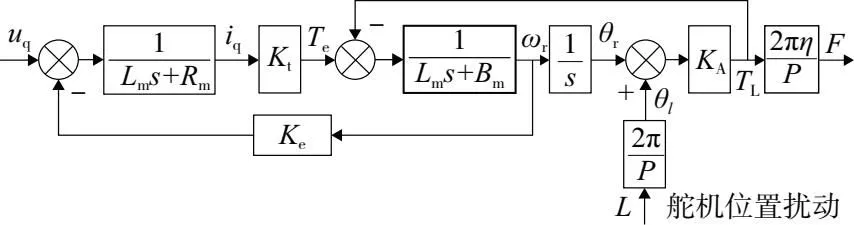
图2 ELLS函数方块图

(3)

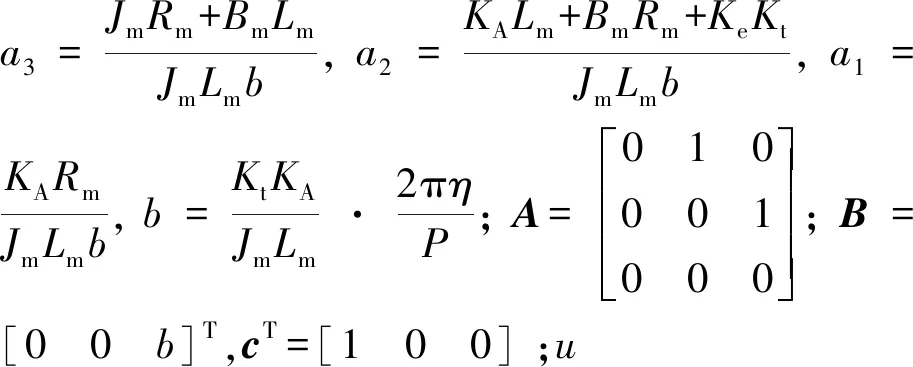
(4)

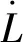
2 控制器和扰动观测器的设计及分析

2.1 目标模型确定

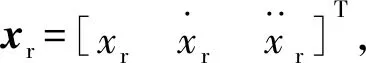
(5)

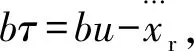
(6)

2.2 基于扰动观测器的RBF神经网络LMI自适应跟踪控制

在实际应用中,d不仅仅包括舵机对系统的扰动,还包括一些摩擦等非线性因素的影响,这些非线性因素的干扰导致d无法准确获得,而LMI作为一种数学工具,已经被广泛地应用到现代控制理论中,主要原因就是控制系统中很多问题都可以转换为LMI系统的可行性问题,即LMI约束下的凸优化问题[8]。

定义扰动观测器为

(7)

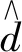
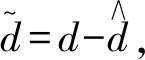
(8)

同样,表达式α(x)往往包括非线性等因素的影响,获取数学模型比较困难,而RBF神经网络可以对任意未知的非线性函数进行逼近[9],因此这里使用RBF神经网络对α(x)进行估计,取RBF神经网络算法为

(9)

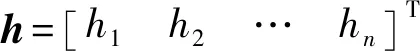
(10)

因此

(11)

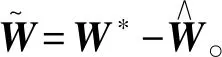
定义控制器设计为

(12)

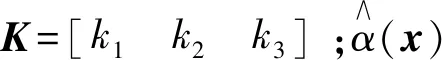
设计李雅普诺夫函数如下

(13)

式中:P>0;P=PT;γ>0。

通过设计P,可以调节e的收敛,并且便于LMI的求解。对式(13)求导,结合式(6)、式(8)、式(11)和式(12),得

(14)

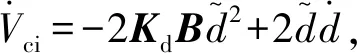
(15)

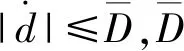
设计RBF神经网络的自适应律为

(16)

(17)

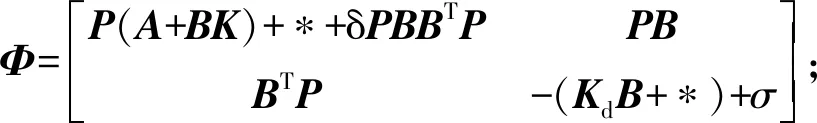
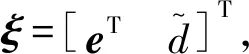
为使不等式收敛,令Φ+αP0<0,α>0,即Φ<-αP0,其中P0=diag{P,I},则存在

(18)

将式(18)左右同乘以diag{P-1,I},令Q1=P-1,N=KQ1,可得第一个LMI为

(19)

式中AQ1+BN+*=AQ1+BN+(AQ1+BN)T。

根据Q1=P-1,P>0,可得第二个LMI为

Q1>0

(20)

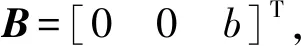
根据以上分析,收敛性分析如下:

(21)

显然闭环收敛结果为,当t→∞时

(22)

增大P的特征值、δ或σ、α的值,可以提高收敛效果。

3 仿真验证

针对以上分析,在MATLAB/Simulink模块搭建式(7)所示的扰动观测器及式(12)所示的RBF神经网络控制器模型,仿真原理如图3所示。

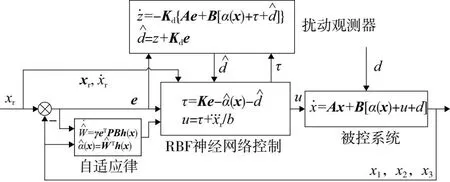
图3 控制仿真示意图

系统中各环节的参数如表1所示。取α=40,δ=10,σ=0.001,经MATLAB的YALMIP工具箱求解LMI的两个不等式(19)、式(20),得扰动观测器的参数Kd、控制器参数K及自适应律参数P,结果如式(23)所示。

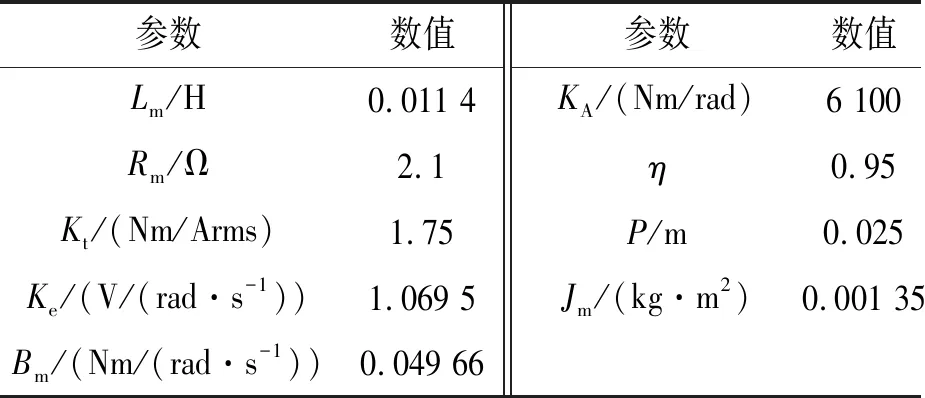
表1 系统各环节参数

(23)

同时,为了充分比较控制器在不同工况下的控制效果,在运动频率相同的前提下,取PMSM做xr=1 000sin(6πt)、xr=1 000sin(10πt)的正弦加载,分别简写为1 000N-3Hz和1 000N-5Hz,直线舵机做L=2sin(6πt)和L=2sin(10πt)的正弦运动,分别简写为2mm-3Hz和2mm-5Hz,给出加入两种观测器后的跟踪误差曲线,如图4所示(本刊黑白印刷,相关疑问咨询作者)。为表示系统的扰动估计效果,图5给出在2mm-5Hz工况下扰动观测器的估计及其误差曲线,图6给出在1 000N-5Hz工况下RBF神经网络对系统非线性项α(x)的估计及其误差曲线。

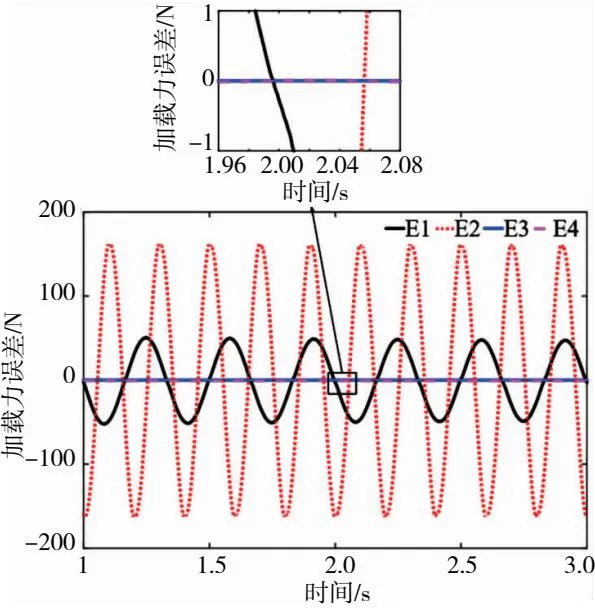
E1—PID,1 000N-3Hz;E2—PID,1 000N-5Hz;E3—LMI,1 000N-3Hz;E4—LMI,1 000N-5Hz

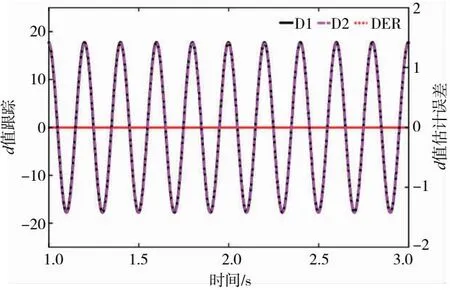
D1—d设定;D2—d估计;DER—d估计误差

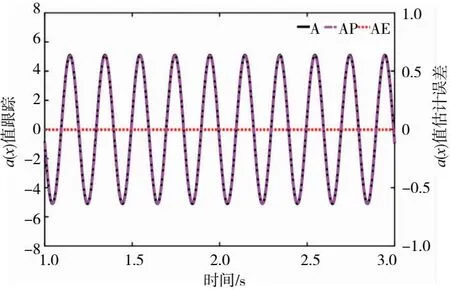
A—α(x)设定;AP—α(x)估计;AE—α(x)估计误差

由图4可知,相对于PID控制,无论是在低频3Hz还是在高频5Hz的工况下,所使用的控制策略在系统稳定运行后都能实现对加载力的准确跟踪,且误差接近0,满足指标,即控制系统拥有很好的鲁棒性,而传统PID控制在实现高精度跟踪时,需要额外的前馈补偿环节,且需要根据不同工况实时调节PID中的3个参数。

由图5可知,在设定的高频工况稳定运行后,扰动观测器的估计值接近舵机运动所造成的位置扰动,而其估计的幅值与设置值的误差在0.1%以内,满足指标,同时将其值引入到控制器中,提高控制器的控制效果。

由图6可知,RBF神经网络对α(x)的幅值估计误差小于1%,相位误差小于1°,均满足“双十指标”,而且幅值误差主要由相位偏移所造成,RBF对非线性项的幅值具有很好的估计性能。

由以上分析可得,扰动观测器和RBF神经网络控制器在较高频率下都能得到很好的控制和估计效果,且跟踪误差在所设定的性能指标内,所提出的控制策略满足高频工况下动态加载准确跟踪。

4 结语

1)对于ELLS动态加载过程中存在的舵机位置干扰和摩擦引起的多余力等问题,基于LMI理论设计系统的扰动观测器和控制器,并通过构造李雅普诺夫函数证明了所提出的控制策略的有效性。

2)通过搭建仿真模型,证明了所提出的扰动观测器和RBF神经网络控制器分别对系统的扰动量和非线性因素的准确估计,且两者的误差均满足“双十指标”,而且通过加入扰动项,证明了所提出的控制器拥有很强的鲁棒性。