基于n值关系语义的命题模态逻辑系统研究

周张泉,杨成彪,刘 军

(1.陆军工程大学 指挥控制工程学院,江苏 南京 210000;2.东南大学 计算机科学与工程学院,江苏 南京 210000;3.南京审计大学金审学院 信息科学与工程学院,江苏 南京 210000)

0 引 言

模态逻辑作为形式化的逻辑语言工具被广泛应用于计算机科学诸多理论和应用中[1],比如软硬件的可靠性模型检测[2-3]、计算复杂性理论[4-5]、数据库理论[6]、知识表示与推理[7]、量子计算[8]等。近年来,模态逻辑越来越多地被研究如何结合神经方式以提升学习模型的可解释性及逻辑推理能力[9-10]。通过引入模态词,模态逻辑具有部分二阶逻辑的表达能力,同时能够保持形式上的简洁性以及较低的计算复杂度[1,11]。研究者基于不同的模态词,发展除了不同的模态逻辑系统,如动态逻辑[12-13]、时序逻辑[14]等。经典的模态逻辑仍旧属于二值逻辑,这使得其在一些常见的应用场景中存在局限性,比如针对知识图谱中分级概念(graded concepts)的推理[15-16](如概念“深红色的花”)、多Agent协同任务[17]等。这些场景要求逻辑语言能够描述对象某一性质的程度(如“深红色”中“深”的程度),或者Agent进行某项决策或行动的可能性。为使得模态逻辑具备上述能力,可建立多值逻辑系统,从而对模态公式的分级程度或可能性进行推理和计算。另外,多值逻辑系统也能更直观地映射到神经方式下的学习模型[18]。

在建立多值逻辑系统方面已有不少研究。早期研究者通过人为指派的方式确定逻辑公式的真值程度[19](又称为真度),然而给全体命题指派真度可行性较低。为解决此问题,诸多研究将全体命题映射为模糊集进行处理,从而提出模糊逻辑的概念[20](fuzzy logic)。模糊逻辑建立了较完整的多值逻辑研究框架,通过将语义模型映射到多值系统以实现多值语义。但该方法容易导致公式真度的弱化,比如重言式和矛盾式的真假是显而易见的,但基于该方法需要做更多假设或处理才能保证。国内学者在逻辑公式真度的建模上也进行了深入的研究[21-25],通过全体命题的真值下界确定命题真度,并将数值计算引入到真度的赋值计算中,建立了计量逻辑学的概念。此种方法更多地考察命题真度的赋值方法,以及如何诱导出复杂公式的真度,但并未从逻辑层面深入探索推理过程在多值语义下是否保持相应的性质,即原有公理系统及推理规则在多值语义下的正确性和完备性。另外,不少工作引入ukasiewicz代数系统以建立多值逻辑系统[20,26-27]。ukasiewicz代数系统具有取值有限性的特点且可以进行任意的n值扩张,相较于复杂代数系统下的计量逻辑在建模难易性与计算效率上具有优势。该方法也被用于建立多值模态逻辑[28-29]。具体而言,给出模态公式在语义模型状态上的真度,同时针对状态间的关系也进行了多值化处理。然而,该方法易导致计算效率较低,且公式的可满足性及有效性并不清晰。在实际应用中,状态间的关系往往是明确的,比如知识图谱中对象或事件的关系、Agent系统中的状态转移关系等。这意味着状态间的可能性及程度信息可以通过公式进行传递,而不需要针对状态间的关系另作多值化处理。这进一步使得公式的可满足性及有效性也能得到更清晰的定义。

1 预备知识

(1)x→Lny=min(1,1-x+y);

(2)x∨Lny=max(x,y);

(3)x∧Lny=min(x,y);

(4)～x=1-x。

称Ln及定义在其上的运算为n值ukasiewicz代数系统。

定义1:设P={p0,p1,…}为可数的命题变元集合,对于n值命题逻辑语言Pn,公式φ归纳定义如下:

其中,p∈P,a∈Ln。定义真度赋值函数V:Pn→Ln如下:

(1)V(p)=c(c∈Ln);

(3)V(φ)=～V(φ);

(4)V(φ∨ψ)=V(φ)∨LnV(ψ);

(5)V(φ∧ψ)=V(φ)∧LnV(ψ);

(6)V(φ→ψ)=V(φ)→LnV(ψ)。

进一步,包含逻辑符号↔的公式所诱导的真度赋值函数为V(φ↔ψ)=V((φ→ψ)∧(ψ→φ))。

给定Pn的公式集Γ及某公式φ,如果对于任意的ψ∈Γ且V(ψ)=1,有V(φ)=1,则称φ是Γ的Ln-后承。针对上述n值命题逻辑语言Pn,可进一步找到一组正确且完备的公理。

定义2:n值命题逻辑公理系统Hn由如下公理组成:

(P1)φ→(ψ→φ);

(P2)(φ→ψ)→((ψ→χ)→(φ→χ));

(P4)((φ→ψ)→ψ)→((ψ→φ)→φ);

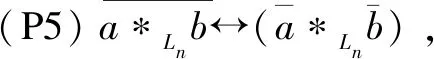
上述公理系统中,公理(P1)～公理(P4)是经典命题逻辑公理,(P5)则包含由Ln系统的数值构成的逻辑公式。给定Pn的公式集Γ及某公式φ,现有公式φ可以通过公式集Γ、上述公理、分离规则以及一致替换规则推导出,则将该推导关系记作Γ├Hnφ。上述公理系统Hn的正确性和完备性由以下定理保证。

定理1:给定Pn(n≥2)的公式集Γ及某公式φ,φ是Γ的Ln-后承,当且仅当Γ├Hnφ。

文献[20]给出了该定理的证明。可以验证,n=2是二值逻辑的情况。

2 n值命题模态逻辑

2.1 n值关系语义

基于上一节介绍的n值ukasiewicz代数系统及其在命题逻辑的扩展,给出n值命题模态逻辑的语法。

定义3:设Q={p0,p1,…}为可数的命题变元集合,对于n值命题模态逻辑语言Qn,模态公式φ归纳定义如下:

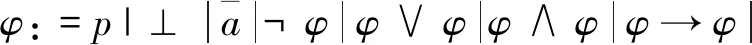
其中,p∈Q,a∈Ln。

下面基于系统Ln给出n值命题模态逻辑语言Qn的关系语义。不同于文献[28-29],这里针对公式在状态上进行n值化处理,同时保持状态间关系的确定性。

定义4:令F=(S,R)为Qn的框架,其中S≠∅为状态集合,R⊆S×S为状态间的二元关系;令M=(F,V)为Qn的模型,其中V:Qn×S→Ln是模态公式在状态上的真度赋值函数,定义如下:

(1)V(p,u)=c;

(3)V(φ,u)=～V(φ,u);

(4)V(φ∨ψ,u)=V(φ,u)∨LnV(ψ,u);

(5)V(φ∧ψ,u)=V(φ,u)∧LnV(ψ,u);

(6)V(φ→ψ,u)=V(φ,u)→LnV(ψ,u);

(7)V(□φ,u)=∧Ln{V(φ,v)|∀v∈S且(u,v)∈R}。

上述式子中,u,v∈S,c,a∈Ln。

根据上述定义,可以进一步导出公式◇φ的真度赋值函数,即:

V(◇φ,u)=∨Ln{V(φ,v)|∀v∈S且(u,v)∈R}

参考文献[30],下面给出Qn的模态公式在模型M上的可满足性定义。

定义5:给定Qn的模型M=(F,V),其中F=(S,R)为Qn的框架,对于模态公式φ,若对于任意状态u∈S,均有V(φ,u)=1,则称φ在M上是有效的,记为VM(φ)=1。若存在某个状态u∈S,有V(φ,u)>0,称φ在模型M的状态u下是可满足的。

可以验证,φ在模型M的某个状态u下是可满足的,当且仅当φ在模型M上不是有效的。对于上述可满足性的定义,若限制V(φ,u)=1,实际上n值命题模态逻辑就转化为了经典的命题模态逻辑。

类似于n值命题逻辑,定义Qn下的Ln-后承如下:给定Qn的模型M、公式集Γ及某公式φ,如果对于任意的ψ∈Γ且VM(ψ)=1,有VM(φ)=1,则称φ是Γ的Ln-后承。

2.2 公理系统

在经典命题模态逻辑中,K系统为最基本的模态逻辑系统[1],其对框架上的状态关系R没有限制。该系统基本构成包括:经典命题逻辑公理、公理K、分离规则MP、必然化规则N以及一致替换规则:

公理K:□(φ1→φ2)→(□φ1→□φ2)

一致替换规则即将上述公理及规则中的公式一致替换为任意其它形式的公式。

以K系统为基础,增加公理及规则可得到其他经典的模态逻辑公理系统。具体而言,在K系统之上增加公理T可得T系统,同时框架上的关系R满足自反性;在T系统之上增加公理4可得系统S4,同时框架上的关系R满足自反性和传递性;在S4上增加公理5可得系统S5,同时框架上的关系R满足自反性和欧性[1]。

公理T:□φ→φ

公理4:□φ→□□φ

公理5: ◇φ→□◇φ

定义6:n值命题模态逻辑系统Kn由n值命题逻辑公理(P1)～公理(P5)、公理K、分离规则MP、必然化规则N、一致替换规则、公理A1以及公理A2组成;系统Tn包含Kn,另外包含公理T;系统S4n包含Tn,另外包含公理4;系统S5n包含S4n,另外包含公理5。

下文利用符号Λn指代某个n值命题模态逻辑系统,其中Λ∈{K,T,S4,S5}。在n值关系语义下,n值命题模态逻辑系统Λn的正确性及完备性尚不明确,下文对此进行探讨。

3 正确性的证明

定理2:针对n值模态逻辑系统Λn,任给Qn的模型M、公式集Γ,对于任意的φ,若Γ├Λnφ,那么有φ是Γ的Ln-后承。

证明:按照如下步骤进行,首先分别证明公理K、公理T、公理4、公理5、公理A1和公理A2的有效性,其次分别证明推导规则MP及规则N的正确性。一致替换规则的正确性由前述推导规则及公理的正确性易证。另外经典n值命题逻辑公理的有效证明性可参考文献[20],在此略过。

(1)公理K的有效性。给定任意n值模型M及公式φ,对于任意的状态u∈S,往证结论V(□(φ1→φ2)→(□φ1→□φ2),u)=1。为证此结论,首先假设V(□(φ1→φ2),u)=c成立,欲使V(□(φ1→φ2)→(□φ1→□φ2),u)=1,根据→Ln定义,需证V(□φ1→□φ2,u)≥c。进一步假设V(□φ1,u)=d,欲使V(□φ1→□φ2,u)≥c成立,只需证V(□φ2,u)≥c+d-1。展开V(□φ2,u)如下:

V(□φ2,u)=∧Ln{V(φ2,v)|∀v∈S且(u,v)∈R}

设存在状态w∈S且(u,w)∈R,使得w=argmin∀t∈S且(u,t)∈RV(φ2,t)成立,于是有V(□φ2,u)=V(φ2,w)。由于V(□(φ1→φ2),u)=c,且(u,w)∈R,有V(φ1→φ2,w)≥V(□(φ1→φ2),u)=c。又由假设V(□φ1,u)=d,有V(φ1,w)≥V(□φ1,u)=d。V(φ1→φ2,w)展开如下:

V(φ1→φ2,w)=V(φ1,w)→LnV(φ2,w)=min(1,1-V(φ1,w)+V(φ2,w))≥c

要使上式成立,即使1-V(φ1,w)+V(φ2,w)≥c,由V(□φ2,u)=V(φ2,w)有1-V(φ1,w)+V(□φ2,u)≥c,进一步有V(□φ2,u)≥c+V(φ1,w)-1,由V(φ1,w)≥d有V(□φ2,u)≥c+d-1。因此得证。

(2)公理T的有效性。给定任意n值模型M及公式φ,对于任意u∈S,往证V(□φ→φ,u)=1。进一步假设V(□φ,u)=c,欲使V(□φ→φ,u)=1,需证V(φ,u)≥c。展开V(□φ,u)如下:

V(□φ,u)=∧Ln{V(φ,v)|∀v∈S且(u,v)∈R}

由于系统Tn需关系R满足自反性,则(u,u)∈R,进一步有V(φ,u)≥V(□φ,u)=c。因此得证。

(3)公理4的有效性。给定任意n值模型M及公式φ,对于任意u∈S,往证V(□φ→□□φ,u)=1。进一步假设V(□φ,u)=c,欲使V(□φ→□□φ,u)=1,需证V(□□φ,u)≥c。任给w∈S,使得(u,w)∈R2,欲使V(□□φ,u)≥c,根据V(□□φ,u)的展开式及w的任意性,只需证V(φ,w)≥c。

展开V(□φ,u)如下:

V(□φ,u)=∧Ln{V(φ,v)|∀v∈S且(u,v)∈R}

由(u,w)∈R2以及系统S4n中关系R的传递性有(u,w)∈R,因此根据上式有结论V(φ,w)≥V(□φ,u)=c成立。因此得证。

(4)公理5的有效性。给定任意n值模型M及公式φ,对于任意u∈S,往证V(◇φ→□◇φ,u)=1。进一步假设V(◇φ,u)=c,欲使V(◇φ→□◇φ,u)=1,需证V(□◇φ,u)≥c。任给v∈S,使得(u,v)∈R,欲使V(□◇φ,u)≥c,只需证V(◇φ,v)≥c。

展开V(◇φ,u)如下:

V(◇φ,u)=∨Ln{V(φ,w)|∀w∈S且(u,w)∈R}=c

因此,存在w∈S且(u,w)∈R,使得V(φ,w)=c。由于系统S5n中关系R具有欧性,有(v,w)∈R,进一步根据V(◇φ,v)的展开式有V(◇φ,v)≥V(φ,w)=c。因此得证。

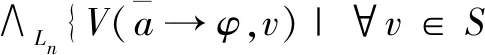
∧Ln{min(1,1-a+V(φ,v))|∀v∈S

且(u,v)∈R}=c

欲使上式结论成立,有∀v∈S且(u,v)∈R,需有1-a+V(φ,v)≥c,即V(φ,v)≥a+c-1。因此得证。

min(1,1-a+V(□φ,u))=c

欲使上式成立,需1-a+V(□φ,u)=c,即V(□φ,u)=a+c-1。展开V(□φ,u)有,欲使V(□φ,u)=a+c-1成立,有∀v∈S且(u,v)∈R,V(φ,v)≥a+c-1成立。因此得证。

下面证明规则的正确性。

(7)分离规则MP的正确性。给定任意n值模型M及公式φ,根据归纳假设有VM(φ)=1,VM(φ→ψ)=1,往证VM(ψ)=1。由VM(φ)=1和VM(φ→ψ)=1有,对于任意状态u∈S,V(φ,u)=V(φ→ψ,u)=1。V(φ→ψ,u)可展开如下:

V(φ→ψ,u)=V(φ,u)→LnV(ψ,u)=min(1,1-V(φ,u)+V(ψ,u))=min(1,V(ψ,u))=1

由于V(ψ,u)≤1,要使上式成立,则有V(ψ,u)=1,由于u的任意性,即有VM(ψ)=1。因此得证。

(8)推导规则N的正确性。给定任意n值模型M及公式φ,根据归纳假设有VM(φ)=1,往证VM(□φ)=1。由VM(φ)=1有,对于任意u∈S,V(φ,u)=1。展开V(□φ,u)如下:

V(□φ,u)=∧Ln{V(φ,v)|∀v∈S且(u,v)∈R}

设存在状态w∈S且(u,w)∈R,并且使得w=argmin∀v∈S且(u,v)∈RV(φ,v),由上式有V(□φ,u)=V(φ,w)。由于u具有任意性,有V(φ,w)=1,进一步有V(□φ,u),因而VM(□φ)=1得证。

证毕。

4 完备性的证明

定义7(极大一致集):任给n值命题模态公式集Ω,Ω是一致的,且不存在任何Ω'⊃Ω,使得Ω'是一致的,则称Ω是极大一致集。

下文用MΛn代表公理系统Λn上所有极大一致集构成的集合。进一步,根据极大一致集的定义,有如下引理。

引理1:任给逻辑系统Λn的极大一致集Ω,对任意n值命题模态公式φ,ψ有:

(3)φ→ψ∈Ω当且仅当φ∉Ω或ψ∈Ω;

(4)φ∧ψ∈Ω当且仅当φ∈Ω且ψ∈Ω;

(5)φ∨ψ∈Ω当且仅当φ∈Ω或ψ∈Ω。

证明 分别针对上述5条结论证明:

证毕。

针对公理系统Λn的典范模型MΛn基于Λn上极大一致集的集合MΛn进行构建。具体定义如下:

定义8(典范模型):对于公理系统Λn,构建模型MΛn=(SΛn,RΛn,VΛn),其中:

(1)SΛn=MΛn;

(2)对于任意的u,w∈SΛn,(u,w)∈RΛn当且仅当,对任意的公式φ∈Qn,若□φ∈u则φ∈w;同时RΛn满足对应系统Λ对关系的要求;

(3)对于所有的命题变元p,VΛn(p,u)=1当且仅当p∈u;

(4)对于任意公式φ,VΛn(φ,u)满足定义4。称模型MΛn为Λn的典范模型。

显然,根据定义4,上述模型MΛn是一个n值命题模态逻辑模型。进一步,由上述定义(2)易得如下推论。

推论1:模型MΛn=(SΛn,RΛn,VΛn)是系统Λn的典范模型,对于任意的u,w∈SΛn,若(u,w)∈RΛn,那么对任意的公式φ∈Qn,当φ∈w时,□φ∈u成立。

在进入完备性证明前,还需证明如下真值引理。

引理2(真值引理):令MΛn=(SΛn,RΛn,VΛn)为逻辑系统Λn的典范模型,对任意u∈SΛn及任意n值模态逻辑公式φ,有VΛn(φ,u)=1当且仅当φ∈u。

证明:施归纳于φ的语法构造。

基础步:当φ为命题变元时,由定义8(3)易证。

(1)φ:=ψ,此时有VΛn(φ,u)=1当且仅当VΛn(ψ,u)=～VΛn(φ,u)=0。根据归纳假设,VΛn(ψ,u)≠1当且仅当ψ∉u。根据引理1(2),ψ∉u当且仅当ψ∈u,即φ∈u。

(2)φ:=ψ∨χ,此时有VΛn(φ,u)=1当且仅当VΛn(ψ∨χ,u)=1,即VΛn(ψ,u)=1或VΛn(χ,u)=1。根据归纳假设,VΛn(ψ,u)=1或VΛn(χ,u)=1,当且仅当ψ∈u或χ∈u,当且仅当(根据引理1(5))ψ∨χ∈u,即φ∈u。

(3)φ:=ψ∧χ,此时有VΛn(φ,u)=1当且仅当VΛn(ψ∧χ,u)=1,即VΛn(ψ,u)=1且VΛn(χ,u)=1。根据归纳假设,VΛn(ψ,u)=1且VΛn(χ,u)=1,当且仅当ψ∈u且χ∈u,当且仅当(根据引理1(4))ψ∧χ∈u,即φ∈u。

(4)φ:=ψ→χ,此时有VΛn(φ,u)=1当且仅当VΛn(ψ→χ,u)=1。展开VΛn(ψ→χ,u)如下:

VΛn(ψ→χ,u)=VΛn(ψ,u)→LnVΛn(ψ,χ)=

min(1,1-VΛn(ψ,u)+VΛn(χ,u))=1

欲使上式成立,需VΛn(χ,u)≥VΛn(ψ,u)。(i)假设VΛn(ψ,u)=1,有VΛn(χ,u)=1,根据归纳假设χ∈u;(ii)假设VΛn(ψ,u)<1,那么VΛn(χ,u)只需满足VΛn(χ,u)≥VΛn(ψ,u)即可。由于VΛn(ψ,u)<1,即VΛn(ψ,u)≠1,根据归纳假设,ψ∉u。因此,VΛn(ψ→χ,u)=1,当且仅当(i)或(ii)成立,当且仅当ψ∉u或χ∈u,当且仅当(根据引理1(3))ψ→χ∈u,即φ∈u。

(5)φ:=□ψ,(⟹)若VΛn(φ,u)=1,即VΛn(□ψ,u)=1。展开VΛn(□ψ,u)如下:

VΛn(□ψ,u)=∧Ln{VΛn(ψ,v)|∀v∈SΛn且(u,v)∈RΛn}

由于VΛn(□ψ,u)=1,因此∀v∈SΛ且(u,v)∈RΛn,有VΛn(ψ,v)=1,根据归纳假设ψ∈v。根据推论5.1,有□ψ∈u,即φ∈u。

(⟸)若φ∈u,即□ψ∈u,任给v∈SΛn使得(u,v)∈RΛn,根据定义8(2)有ψ∈v,根据归纳假设,VΛn(ψ,v)=1。展开VΛn(□ψ,u)如下:

VΛn(□ψ,u)=∧Ln{VΛn(ψ,v)|∀v∈SΛn且(u,v)∈RΛn}

由VΛn(ψ,v)=1及v任意性,有VΛn(□ψ,u)=1。

证毕。

下面可进一步完成完备性的证明。

所寻找的模型为Λn的典范模型MΛn=(SΛn,RΛn,VΛn)。令Γ'为Λn的极大一致集,且Γ'⊃Γ,有Γ'∈SΛn。

(1)对于任意的ψ∈Γ,有ψ∈Γ',根据引理2进一步有VΛn(ψ,Γ')=1。

综合(1)和(2)可证上述逆否命题。

证毕。

5 结束语