部分相干多离轴涡旋矢量光束的传输特性*

徐华锋 张兴宇 王仁杰

(安徽理工大学力学与光电物理学院,淮南 232001)

1 引言

部分相干光的存在具有普遍性,并且在许多应用领域,部分相干光束比完全光束更具有优越性,例如,部分相干光能够有效克服大气湍流负效应影响[1–3];基于随机光场相干结构调控的光学加密在复杂环境中具有较好的鲁棒性[4].因此,部分相干光束的研究与应用一直以来是光学领域中的热点课题[1–6].近年来,得益于Gori 等[7,8]提出的构建部分相干光束关联函数的限定条件,系列具有非传统(非高斯函数形式)的特殊关联结构函数的部分相干光束受到了广泛的关注与研究[9–13].大量研究表明,具有特殊空间关联结构的部分相干光束展现出许多奇特性质,如厄米-高斯关联结构的部分相干光束在传输过程中展现出自分裂与自愈合特性[9];非均匀关联部分相干光束在传输过程中展现出自偏移与自聚焦特性[10];拉盖尔-高斯关联结构的部分相干光束经过聚焦后可以在焦点附近产生三维可控的光学囚笼[11]等.2014 年,Mei[12]和Liang 等[13]分别从理论和实验上研究了具有矩形对称的余弦-高斯关联结构(RCGSM)的部分相干光束,并揭示了该光束在传输过程中具有自分裂特性而产生4 个相同的子波瓣.这些结果表明,通过调控部分相干光束的空间关联结构是塑造和构建特定结构光场的一种有效方法,在自由空间光通信、衍射成像和光学微操纵等领域具有重要的应用价值[14,15].

涡旋光束是一种具有螺旋相位波前的特殊结构光束,因其携带有轨道角动量和位相奇点等特点,在光学微操控、光学通信、量子信息和表面等离激元等领域具有广泛的应用[16–21].涡旋光束的产生方法有很多,常用的有螺旋相位板、计算全息法和空间光调制器转换法等[22,23].通常,在实验中利用螺旋相位板或叉型相位全息图产生涡旋光束时,为了将涡旋相位嵌入到光束波前中,需将涡旋相位中心与光束中心严格对准.然而,在实际操作中由于对准误差的原因,两者之间会存在一定程度的偏离,从而会产生离轴涡旋光束[24].因此,研究离轴涡旋光束的传输与聚焦特性更具有实际的研究意义和价值.有研究表明,离轴涡旋相位可以打破轴向能流的旋转对称性,而且多个离轴涡旋相位可以引起聚焦光场强度的重新分布和构建,这为涡旋光束传输特性的调制提供了一种新的调控手段[25–27].

本文以具有分裂特性的RCGSM 光束为对象,将多个离轴涡旋相位引入其中,构建一种携带多个离轴涡旋相位的径向偏振RCGSM 光束的理论模型,数值模拟了携带3 个和4 个离轴涡旋相位的径向偏振RCGSM 光束通过薄透镜后聚焦光强和偏振态分布的演化情况,探讨了多个离轴涡旋相位的调控对每个子波瓣的调制效果,并分析了光束阶数和相干长度对光束传输特性的影响,同时还探讨了该光束通过障碍物后的自修复能力.本研究结果将在光学微操控和光学加密等领域有着重要应用价值.

2 理论模型构建

在直角坐标系中,径向偏振光束可以看作是由x偏振方向的HG10模式和y偏振方向的HG01模式的相干叠加[28,29]:

式中,w0为径向偏振高斯光束的束腰宽度,Ex(r,ω)和Ey(r,ω) 分别表示源平面r≡(x,y) 处角频率为ω的电场在x和y方向上的分量,ex和ey分别表示x和y方向上的单位矢量.

基于相干偏振统一理论,在空间-频率域中,部分相干径向偏振光束的二阶统计特性可以用2×2 阶交叉谱密度矩阵来表示[30]:

其中,矩阵元为

式中,“*”表示复共轭运算,〈·〉表示系统平均.为了简化,在下面公式推导中,所有推导物理量中的频率将被省略,但其依赖性仍然隐含在其中.

为了成为数学上可实现的真实交叉谱密度函数,其矩阵元必须满足以下正定条件[8]:

其中,Hx(r,v) 和Hy(r,v) 为任意函数,v=(vx,vy)是傅里叶平面上空间频率矢量;pαβ(v) 是2×2 权重矩阵(v) 的矩阵元,即:

需要满足以下非负的限定性条件:

另外,为了要构建出高斯-谢尔模源,核函数Hα(r,v)应具类似的傅里叶结构,即:

其中,k=2π/λ是波数,λ是波长;位置矢量r和r′分别是相对于光轴O和涡旋中心O′来定义的.因此,光束轮廓函数Fα(r) 是关于光轴对称,而涡旋函数f(r′) 是关于涡核中心对称[26,31].如图1(a)所示,以光束中心O为坐标原点,假定有N0个离轴涡旋相位,其中第j个涡旋中心与光束中心偏离的位移矢量为sj=(sxj,syj) ,坐标分别为sxj=s0cos[(j-1)2π/N0] 和syj=s0sin[(j-1)2π/N0],则位置矢量的关系可以表示为=r-sj[26].特别地,当偏移量s0=0 时,涡旋相位中心与光束中心重合,表示为轴上涡旋相位.

城市形象，是一个城市在发展过程中非常重要的吸引力资源，只有通过有效的传播才能产生价值。塑造鲜明而具有个性化的形象，能带来巨大的城市吸引力，进而带来丰富的人流、物流、信息流，增强城市的核心竞争力。事件营销，在城市形象塑造的过程中发挥着巨大的推动作用。事件在传播过程中所带来的关注度、辐射度、影响力，对城市形象的传播、城市品牌的树立都有着不可替代的作用。

图1 (a)源平面处第j 个离轴涡旋中心与观察点的位置矢量关系;(b)—(d)携带3 个离轴涡旋相位(拓扑荷数l=1)的径向偏振RCGSM 光束在源平面处的(b)离轴涡旋相位排列、(c)离轴涡旋相位分布和(d)光强分布Fig.1.(a) An illustration of the position vector relationship between the j-th off-axis vortex phase core and the observation point in the initial plane;(b) arrangement of three off-axis vortex phases,(c) phase distribution,and (d) intensity distribution of a radially polarized RCGSM beam carrying three off-axis vortices in the source plane,respectively.

本文为了构建出具有直角对称的余弦-高斯形式关联结构的径向偏振光束[26],并将多个离轴涡旋相位均匀地引入其中,核函数设定为

权重函数[12,13]为

径向偏振RCGSM 光束是一类具有特殊空间关联结构的高斯-谢尔模光束,是一种真实存在的部分相干光束,其数学函数满足麦克斯韦方程和亥姆霍兹方程的解,且能稳定传输[12,13].Liang 等[13]在实验上利用空间光调制器(SLM)与旋转的毛玻璃片(RGGD)的组合产生了RCGSM 光束.若将该光束通过一个径向偏振转换器件,从而得到径向偏振RCGSM 光束.此外,再利用全息计算法设计产生多个离轴的叉型相位光栅图加载到SLM 上,从而将多个离轴涡旋相位引入到光束中,便可以产生出携带多个离轴涡旋相位的径向偏振RCGSM 光束.

为了能够直观理解携带多个离轴涡旋相位的矢量光束模型,在图1(b)—(d)分别给出了携带3 个离轴涡旋相位的径向偏振RCGSM 光束的相位排列方式、相位分布和光强分布.在源平面处,3 个离轴涡旋相位相对于光束中心O均匀排列(如图1(b),(c)所示),径向偏振光束中心因具有偏振奇点缘故而强度为零,呈现暗中空结构分布,而光束的半腰宽上分布着与离轴涡旋相位中心相对应的3 个空心暗核(见图1(d)).

3 基于ABCD 光学系统的传输理论

在傍轴近似条件下,部分相干矢量光束在源平面处被不透明的障碍物遮挡后并通过ABCD光学系统时,在z>0 处的接受平面上交叉谱密度函数矩阵元可以利用菲涅尔-惠更斯原理来表示[32,33]:

此处,ρ1和ρ2表示输出平面内横截面上的位置矢量,A,B,C和D表示ABCD光学系统的变换矩阵元.式中T(ri) 表示不透明障碍物的透过率函数,具有高斯振幅吸收率的圆形障碍物的透过率函数可以表示[33]:

其中,r0=(x0,y0) 和wd分别表示圆形障碍物的中心坐标和尺寸.而扇形障碍物的透过率函数T(θ)可表示为[34,35]

式中,符号“⊗”表示卷积运算.

在输出平面上的总光强可以表示为

其中,Ixx(ρ,z) 和Iyy(ρ,z) 分别表示聚焦光强在x和y的光强分量.

另外,可以认为部分相干矢量光束的交叉谱密度是完全偏振部分成分和完全非偏振部分成分之和,而完全偏振部分的偏振态可以用偏振椭圆来表征,其椭圆的长半轴A1和短半轴A2,椭圆度ε和方位角θ可以用交叉谱密度矩阵元来表示[37]:

(21)式中的符号 “+”和“–”分别对应椭圆的长半轴A1和短半轴A2的表达式,Re 表示取实部.将(14)式—(17)式代入(21)式—(23)式中,可以研究携带多个离轴涡旋的径向偏振RCGSM 光束通过透镜后的偏振态分布.

4 数值模拟与分析

4.1 聚焦光强

首先采用数值方法研究部分相干多离轴涡旋矢量光束在通过薄透镜后的聚焦特性,薄透镜的焦距为f.利用上文的推导结果和MATLAB 软件,(15)—(17)式的积分运算可以利用MATLAB快速傅里叶变换(FFT)算法和卷积定理来计算.源平面和接受平面的变换矩阵可以表示为[36]

在数值计算中,取光束波长λ=632.8 nm,束腰半径w0=1 mm ,涡旋相位离轴距离s0=0.5w0,每个离轴涡旋相位的拓扑荷数l=1,透镜的焦距f=400 mm,图2 和图3 中右下标横线代表了每个图的四分之一大小.

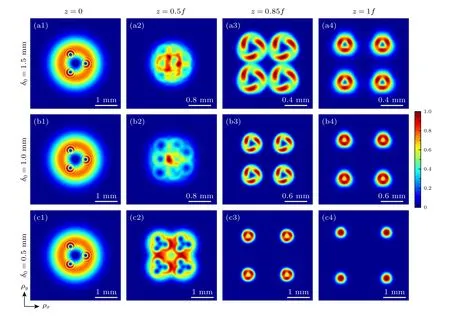
图2 当光束阶数 m=n=5 时,携带3 个离轴涡旋相位的径向偏振RCGSM 光束通过薄透镜后的聚焦光强演化Fig.2.Evolution of the focused intensity of a radially polarized RCGSM beam carrying three off-axis vortex phases through a thin lens when the beam order m=n=5 .

图3 当光束阶数 m=n=5 时,携带4 个离轴涡旋相位的径向偏振RCGSM 光束的聚焦光强演化Fig.3.Evolution of the focused intensity of a radially polarized RCGSM beam carrying four off-axis vortex phases through a thin lens when the beam order m=n=5 .

图2 和图3 分别表示光束阶数m=n=5 时,携带3 个和4 个离轴涡旋相位的径向偏振RCGSM光束在不同相干长度δ0下通过薄透镜后的聚焦光强演化情况.如图2 和图3 第1 列所示,在源平面处,径向偏振光束中心因具有偏振奇点缘故而强度为零,呈现暗中空结构分布.此外,由于涡旋相位中心具有相位奇点,因此在光束的半腰宽上分布着与离轴涡旋相位中心相对应的多个空心暗核.由于径向偏振RCGSM 光束因其独特的空间相干结构而表现出自分裂特性,可以分成4 束完全相同的子波瓣,该结果与文献[12,13]结果一致.此外,本课题组前期研究表明,多离轴涡旋相位可以引起聚焦光强的重新分布与构建[26].更有意义的是,这种多离轴涡旋相位调制效果可以作用在每个子波瓣上.如图2 和图3 第1 行所示,在相干长度较大的情况下(δ0=1.5 mm),光束在自分裂的过程中,每个子波瓣的光强在多离轴涡旋相位调制下旋转聚焦与重构,最后在焦平面处分别形成了三角形(图2(a4))和正方形(图3(a4))空心光强分布.由此可发现,通过调控离轴涡旋相位的数量N0,从而可以调控每个子波瓣的光强分布,产生4 束相同的多边形空心光强阵列.当相干长度较小时,光束的分裂演化速度加快,且子波瓣之间的间距变大.然而,当相干度特别小时(如图2 和图3 最后一行所示,δ0=0.5 mm),部分相干光束的相干性调控占主导作用,离轴涡旋相位在每个子波瓣的调制效果逐渐消失,由于低相干性引起的光强退化效应严重,每个子波瓣呈现准高斯光强分布.

图4 和图5 分别给出了光束阶数m=n=5和相干长度δ0=1.5 mm 时,携带4 个离轴涡旋相位的径向偏振RCGSM 光束通过薄透镜后的偏振态演化情况.作为对比,图中第1 行为无障碍物时的光强演化情况.利用不同角度的扇形障碍物和不同尺寸的圆形障碍物遮挡住其中一个离轴涡旋相位.如图4 和图5 的第2 行所示,当障碍物相对较小时,光束仍具有一定的自修复能力.然而,当障碍物尺寸较大时,将其中一个离轴涡旋相位完全遮挡住,此时叶瓣的强度分布遭到破坏,导致每个子波瓣会出现不同程度的“缺口”.此外,当相干度较小时,部分相干光束的空间相干性调控占主导作用,部分相干光束能够表现出更强的自修复能力[35],但每个子波瓣的光强退化为高斯形式分布.

图4 当光束阶数 m=n=5 和相干长度 δ0=1.5 mm 时,携带4 个离轴涡旋相位的径向偏振RCGSM 光束通过扇形障碍物的聚焦光强演化Fig.4.Evolution of the focused intensity of a radially polarized RCGSM beam carrying four off-axis vortex phases after passing through a sector-shaped opaque obstacle when the beam order m=n=5 and coherent length δ0=1.5 mm .

图5 携带4 个离轴涡旋相位的径向偏振RCGSM 光束通过圆形障碍物后的聚焦光强演化( m=n=5 ,δ0=1.5 mm)Fig.5.Evolution of the focused intensity of a radially polarized RCGSM beam carrying four off-axis vortex phases after passing through a circular obstacle when the beam order m=n=5 and coherent length δ0=1.5 mm .

4.2 偏振态分布

图6 为携带3 个和4 个离轴涡旋相位的径向偏振RCGSM 光束通过薄透镜后的偏振态演化情况.在源平面处(z=0),光束的偏振态呈现径向偏振分布,但在传输过程中,由于光束的自分裂特性和离轴涡旋相位的影响,其径向偏振态逐渐转化为每个子波瓣上的椭圆偏振态或圆偏振态分布,这表明在涡旋光束的聚焦过程中,其携带的轨道角动量逐渐转化为每个子波瓣上的自旋角动量.如图6 所示,径向偏振逐渐演化成与4 个光束子波瓣相对应的左旋椭圆偏振分布(拓扑荷数l=1)并呈顺时针旋转,最后在焦平面处每个子波瓣上的偏振态分别呈现倒三角形(N0=3)和斜正方形分布(N0=4).

图6 当光束阶数 m0=n0=5 和相干长度 δ0=1.5 mm 时,携带多个离轴涡旋相位的径向偏振RCGSM 光束通过薄透镜后的偏振态演化情况Fig.6.Evolution of the state of polarization of radially polarized RCGSM beams carrying multiple off-axis vortex phases through a thin lens when the beam order m0=n0=5 and coherent length δ0=1.5 mm .

图7 和图8 分别为光束阶数m0,n0和相干长度δ0对携带3 个和4 个离轴涡旋相位的径向偏振RCGSM 光束在焦平面处偏振态分布的影响.如图7 和图8 第1 列所示,当光束阶数较小(如m0=n0=1)或相干度较大(如δ0=1.5 mm)时,光束并未完全分裂,因而光束子波瓣之间的偏振态有相互交叠现象.如图7 所示,当光束阶数m0,n0逐渐增大时,光束完全分裂后,偏振态之间没有交叠,每个子波瓣光强呈现三角形或正方形空心强度分布,而其偏振态则呈现倒三角形或斜正方形分布且保持不变.如图8 所示,当相干长度δ0逐渐减小时,光束完全分裂后,每个子波瓣的光强由三角形或正方形空心强度分布退化成准高斯分布,而其偏振态仍呈现倒三角形或斜正方形分布并保持不变.因此,当光束子波瓣完全分离后,光束阶数m0,n0和相干长度δ0对偏振态的分布并无太大的影响.

图7 当相干长度 δ0=1.5 mm 时,光束阶数 m0,n0 对携带多个离轴涡旋相位的径向偏振RCGSM 光束在焦平面处偏振态分布的影响Fig.7.Influences of beam order m0,n0 on the distribution of the state of polarization of radially polarized RCGSM beams carrying multiple off-axis vortex phases in the focal plane when the coherent length δ0=1.5 mm .

图8 当光束阶数 m0=n0=2 时,相干长度 δ0 对携带多个离轴涡旋相位的径向偏振RCGSM 光束在焦平面处偏振态分布的影响Fig.8.Influence of coherent length δ0 on the distribution of the state of polarization of radially polarized RCGSM beams carrying multiple off-axis vortex phases in the focal plane when the beam order m0=n0=2 .

图9 为携带多个离轴涡旋相位的径向偏振RCGSM 光束通过不同角度的扇形障碍物后在焦平面处的偏振态分布.如图9 所示,当光束通过障碍物后,光束的一个离轴涡旋相位被遮挡,不仅每个子波瓣的强度分布遭到破坏,而且其偏振态也会遭到破坏,变成了左右对称结构的偏振分布.即使在相干度较小时,光强具有较强的自修复能力,其偏振态都无法完成自修复.

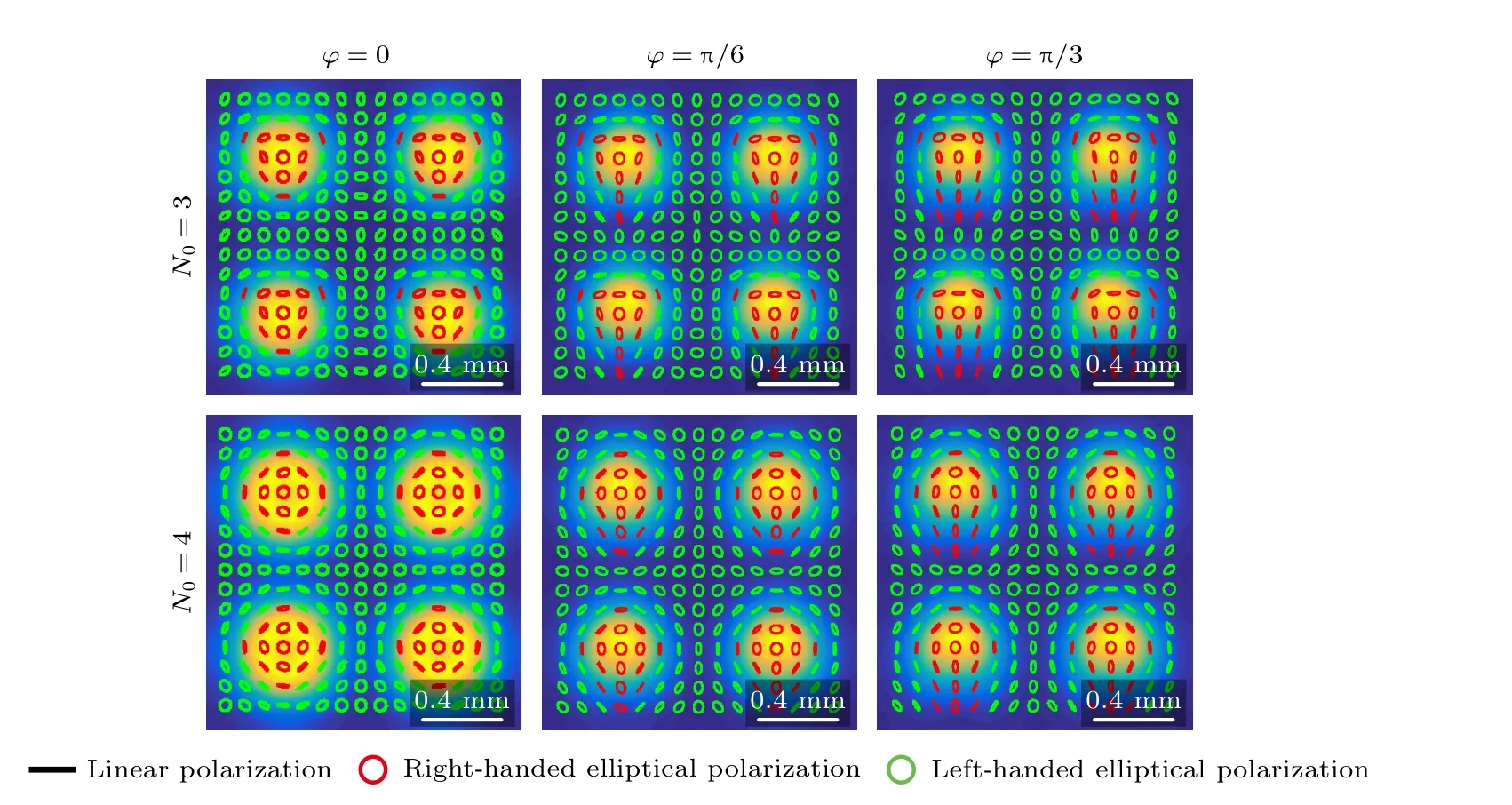
图9 当光束阶数 m=n=2 和相干长度 δ0=0.5mm 时,携带多个离轴涡旋相位的径向偏振RCGSM 光束通过扇形障碍物后在焦平面处的偏振态分布Fig.9.Distribution of the state of polarization in the focal plane for the radially polarized RCGSM beams carrying multiple off-axis vortex phases through a sector-shaped opaque when the beam order m=n=2 and the coherent length δ0=0.5 mm .

5 结论

基于部分相干光的相干与偏振的统一理论,采用傅里叶变换和卷积定理的方法,研究了携带多个离轴涡旋相位的径向偏振RCGSM 光束通过薄透镜后的聚焦光强和偏振态分布等聚焦特性.研究表明,该光束因其独特的空间相干结构而具有自分裂特性,可以产生4 个相同的子波瓣.此外,多离轴涡旋相位可以对每个子波瓣的光强和偏振态分布进行调制.当相干长度较大时,在相干性和多离轴涡旋相位的共同调制下,光束可以在焦平面处产生4 个具有多边形空心光强分布的光斑阵列,而每个子波瓣的多边形强度分布与离轴涡旋数量N0有关;当相干度较小时,光束的相干性调控占主导作用,而多个离轴涡旋相位对子波瓣的光强调制效果消失,每个子波瓣的光强退化成准高斯形式分布.当光束完全分裂后,每个子波瓣上的偏振态呈现出与光强对应的斜多边形椭圆分布并保持不变,与光束阶数和相干长度无关.另一方面,若用一个扇形或圆形障碍物将其中的一个离轴涡旋相位遮挡住,则会破坏每个子波瓣的强度分布和偏振分布,在每个子波瓣上产生不同程度的光强缺口.总之,本文研究揭示了携带多个离轴涡旋相位的径向偏振矢量光束的聚焦特性,通过联合调制部分相干光束的空间关联结构和多个离轴涡旋相位,可以实现对光束阵列中子波瓣的光强和偏振态的调控,在微粒操控和光学加密等领域有着重要应用前景.