不导水断层构造的二维瞬变电磁响应特征研究
乔元栋,杨振强,焦俊俊,牛兴国,兰永青,谭丁瑞
(1.山西大同大学建筑与测绘工程学院,山西 大同 037003;2.内蒙古农业大学能源与交通工程学院,内蒙古 呼和浩特 010018;3.中国矿业大学(北京)地球科学与测绘工程学院,北京 100083;4.内蒙古自治区有色地质勘查局,内蒙古 呼和浩特 010010;5.山东正元地球物理信息技术有限公司,山东 济南 250101)
0 引 言
煤炭资源在我国能源结构中占据着不可或缺的地位,随着煤炭资源开采的强度和深度不断突破,采煤工作面在掘进过程中易受到采煤面前方或附近不良地质构造的威胁而引发煤矿安全开采事故[1-2],其中断层是主要的威胁来源之一。
采煤工作面开采过程中,受超前支承压力影响,围岩的应力场平衡被打破,致使岩层变形破坏,极易导致断层活化,从而造成工作面垮落、突水等地质灾害,严重威胁煤矿人员的生命安全和财产安全[3],因此,对矿井工作面前方隐伏断层进行超前探测与精细资料解释能有效地避免事故发生,保障人员生命安全,避免财产损失。一般而言,矿井断层分为活化导水断层和不导水断层,两种断层的电学性质截然不同。通常情况下,断层如果活化导水,地球物理特征表现为低电阻率;断层如果不导水,表现为高电阻率[4]。瞬变电磁法可以通过这一特征有效探测断层。近年来,学者们在断层探测方面进行了大量的研究。李凯等[5]采用三维多尺度时域有限差分法分析了不同位置和测点的矿井顶底板充水断层构造响应规律,认为响应电压幅值与测点到断层的垂向距离和横向距离存在联系。焦险峰等[6]采用物理模拟的手段研究了走向导水断层的瞬变电磁超前探测的视电阻率响应规律。ZHANG 等[7]结合实际野外地质断层构造的地电特征,应用三维时域有限差分法模拟了断层构造的瞬态响应特性,建立了适用于城市浅层断层的瞬变电磁野外观测系统。胡雄武等[8]采用全空间瞬变电磁三维时域有限差分法对掘进前方导水断层进行了模拟,总结了断层模型的距离、尺寸及富水性等参数的响应特征。杨海燕等[9]采用圆锥型瞬变电磁发射装置实现了对浅层露头断层的探测。周超等[10]采用等值反磁通瞬变电磁技术和微震技术的综合地球物理手段探测隐伏断层的位置和走向。韩自强等[11]综合瞬变电磁二维反演和地震波速成像结果,预报了断层破碎带的位置及富水情况。周逢道等[12]设计的高带宽多匝接收小线圈能有效提高浅层断层的分辨率。刘伟等[13]采用瞬变电磁法、高密度电阻率法、微动和土壤氡气的综合地球物理方法,获得了隐伏断裂的位置、性质、产状和规模。
上述研究的对象主要集中于导水的低电阻率断层,原因是瞬变电磁法对低电阻率尤为敏感,相反,对高电阻率的响应规律还不够明确。然而,高电阻率断层在煤矿井下也普遍存在,并且已成为矿井安全隐患的主要挑战之一,仅通过钻探的形式探查无疑增加了成本。另外,现有的研究成果对于断层模型的正演模拟普遍采用三维有限差分法,然而,实际地下隐蔽断层体多为不规则形态,有限差分法的网格剖分方式会导致模拟精度的急剧下降,而有限单元法的非结构网格剖分形式适用于复杂的不良地质体。因此,本文采用二维有限单元法探索研究高电阻率断层影响下的瞬变电磁法超前探测的响应特征。
1 理论分析
1.1 二维瞬变电磁控制方程
在均匀各向同性、非磁性的导电介质中,假设eiωt与时间相关,有源场的电场E和磁场H由麦克斯韦方程表达,计算见式(1)和式(2)。
式中:Ms和Js分别为外加磁流源密度和电流源,Js=iωPs,Ms=iµ0ωMS,其中,PS为电单极子,MS为磁单极子;阻抗zˆ=iµω ,yˆ=σ+iµω。对式(1)、式(2)中电场E和磁场H进行傅里叶变换[14],计算见式(3)。
式(4)和式(5)中k2=−,=−k2,其他分量由和的空间导数求得,具体计算见式(6)~式(9)。
1.2 二维瞬变电磁的有限元方程
本文采用伽辽金法[17]对式(4)和式(5)进行求解,并推导出二维瞬变电磁有限元方程,具体计算见式(10)。
具体推导过程见文献[18] 附录A,本文不再赘述。需要说明的是,本文采用迭代法求解有限元线性矩阵方程。
2 算法验证
在直角坐标系下,均匀全空间二维模型大小为300 m×260 m,取背景电阻率ρ=100 Ω·m,回线源边长为3 m ×3 m,发射电流为4 A,采样开始时刻为0.01 ms,分别计算了瞬变电磁二维有限单元法数值解与一维解析解以及二者的相对误差,计算结果如图1 所示。由图1 可知,二维有限单元法数值解与一维解析解吻合度整体上较好,相对误差曲线在采样早期发生振荡,最大达到了13%。但随着采样延时的逐渐增大,相对误差迅速减小且趋于0.1%,表明本文瞬变电磁二维时域有限单元法的正演精度较高,满足模拟的精度要求。

图1 二维有限单元法瞬变电磁均匀空间算法验证Fig.1 Verification of transient electromagnetic uniform space algorithm by 2D finite element method
3 模型试算
3.1 掘进巷道断层模型建立
我国煤矿成煤的典型特征大多数为层理构造,如砂岩、煤层、泥岩、灰岩等,在地下成层交替分布。本文以常见采煤工作面超前探测模型为研究对象,综合我国西部常见煤系地层的特征,即顶板砂岩层、底板砂岩层、煤层和灰岩层作为超前探测模型中的层状介质,分别建立无断层超前探测模型和含断层超前探测模型,模型如图2 所示,模型大小为300 m×260 m,巷道高5 m,从X方向−150 m 处至X方向0 m 处,共计150 m,煤层厚度5 m,从X方向0 m处至X方向150 m 处,共计150 m。含断层模型中,在巷道迎头面前方30 m 处发育一正断层,断层倾角60°,落差25 m,宽度为5 m。表1 为模型图的各岩层地电参数。
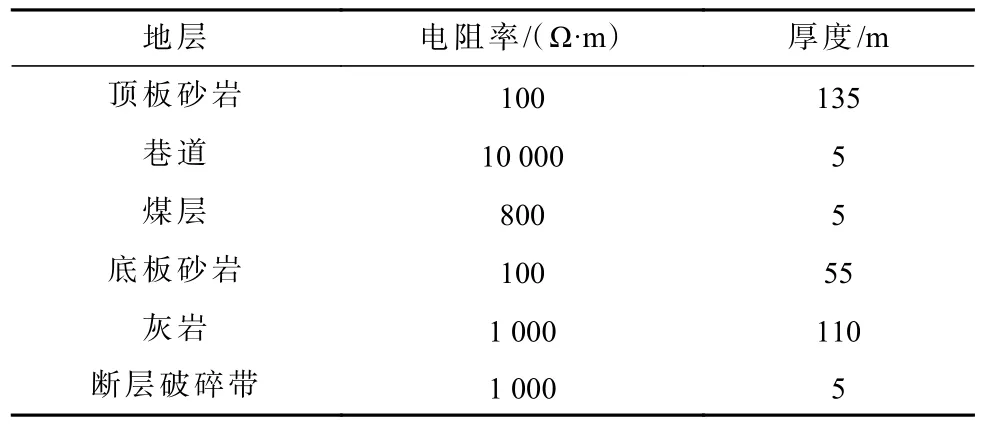
表1 模型地电参数Table 1 Geoelectric parameters of model
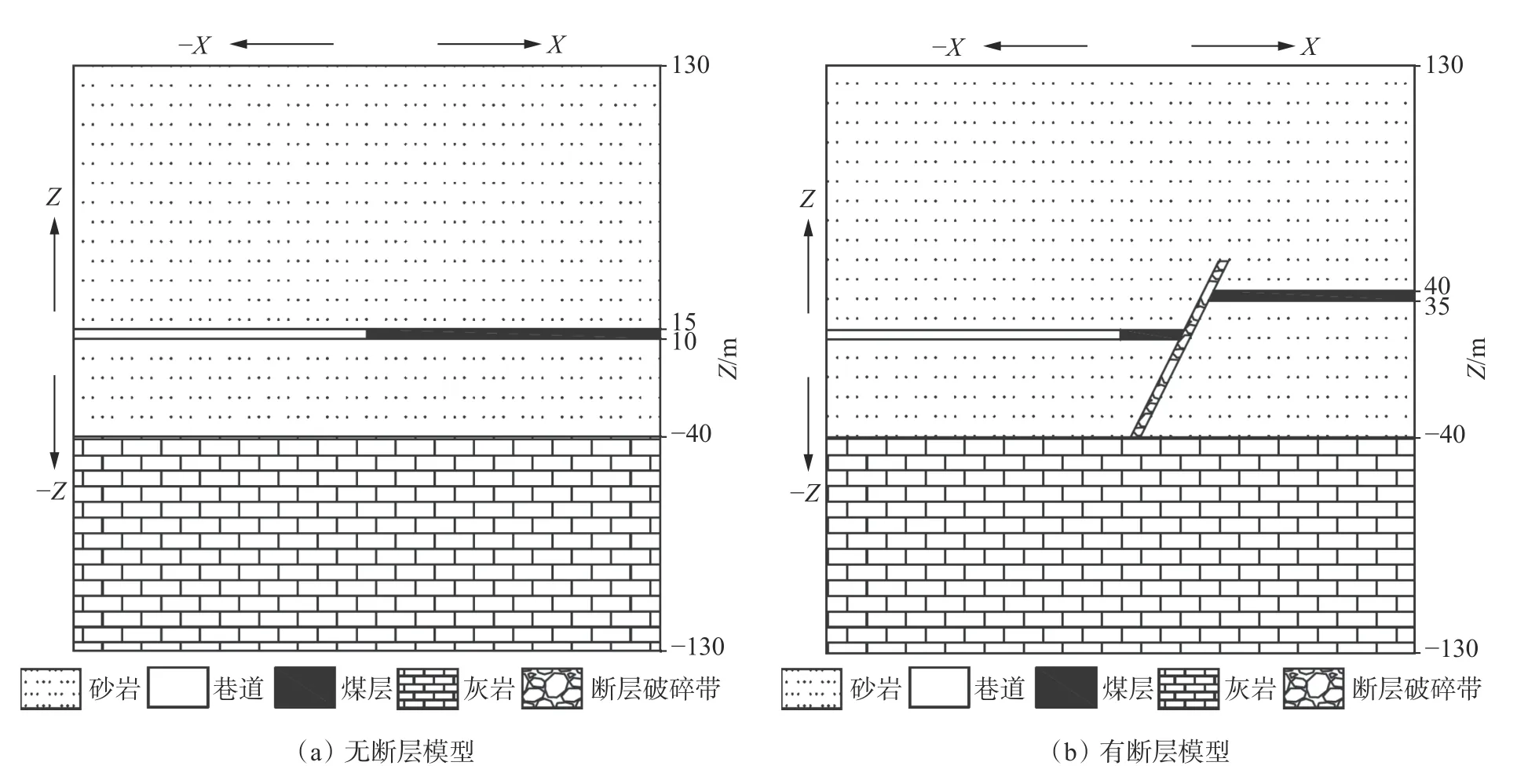
图2 掘进巷道瞬变电磁法超前探测地质模型Fig.2 Geological model of transient electromagnetic method for advanced detection of tunneling roadway
3.2 参数设置
本文采用二维有限单元法对瞬变电磁场控制方程进行数值计算,发射线圈3 m×3 m,共60 匝,发射电流4 A,接收线圈采用发射线圈接收感应二次场,收-发射线圈采用重叠回线观测方式平行敷设于巷道迎头面,发射线圈的起点坐标为(0, 14),终点坐标为(0, 11),关断时间设置为1 μs,采样延时0.06~5.00 ms,在巷道迎头面布置一条测线,测线沿X方向0 m、Y方向15 m 处至X方向0 m、Y方向10 m 处,测线长5 m,测点点距0.5 m,共11 个测点。
3.3 感应磁场响应特征
为了对比总结断层影响下的瞬变电磁响应规律,对图2 中的无断层模型和有断层模型分别进行了模拟计算,计算结果如图3~图6 所示,横轴是水平距离,纵轴是垂直距离,分别计算了0.06 ms 和0.10 ms时刻的无断层模型和有断层模型的感应磁场响应,图3~图6 中(a)是磁场X分量等值线图,(b)是磁场Y分量等值线图,(c)是总磁场等值线图。

图3 无断层模型瞬变电磁0.06 ms 扩散磁场等值线图Fig.3 The contour map of 0.06 ms induced magnetic field of transient electromagnetic without fault model
由图3 和图4 可知,磁场X分量的正值集中分布于底板区域,负值集中分布于顶板区域,这表明感应磁场的正值为瞬变场的正向磁场,负值为反向磁场。随着采样时间的延长,感应磁场逐渐向模型边界扩散传播,呈现近椭圆形的“烟圈”形状。磁场Y分量的正值集中分布于煤层所在的右半区域,负值集中分布于巷道所在的左半区域,随着采样时间的延长,感应磁场逐渐向模型边界扩散传播,呈现近椭圆形的“烟圈”形状。总磁场的总体扩散规律符合“烟圈”的特征,但当电流关断后的0.06 ms 时刻,在发射回线的周围呈现出负值,这表明在关断时间后的极短时间内,发射线圈先是感应出二次正向磁场,并快速向模型四周扩散。随着采样时间的延长,在发射线圈周围感应出二次反向磁场,反向磁场的分布范围呈现扩散趋势。推断反向磁场产生原因是在两种电阻率差异较大的介质接触面会形成积累电荷,积累电荷形成电场并随时间变化,变化的电场产生变化的磁场。总体而言,磁场X分量、Y分量以及总磁场的感应二次磁场对巷道空气层几乎没有响应。
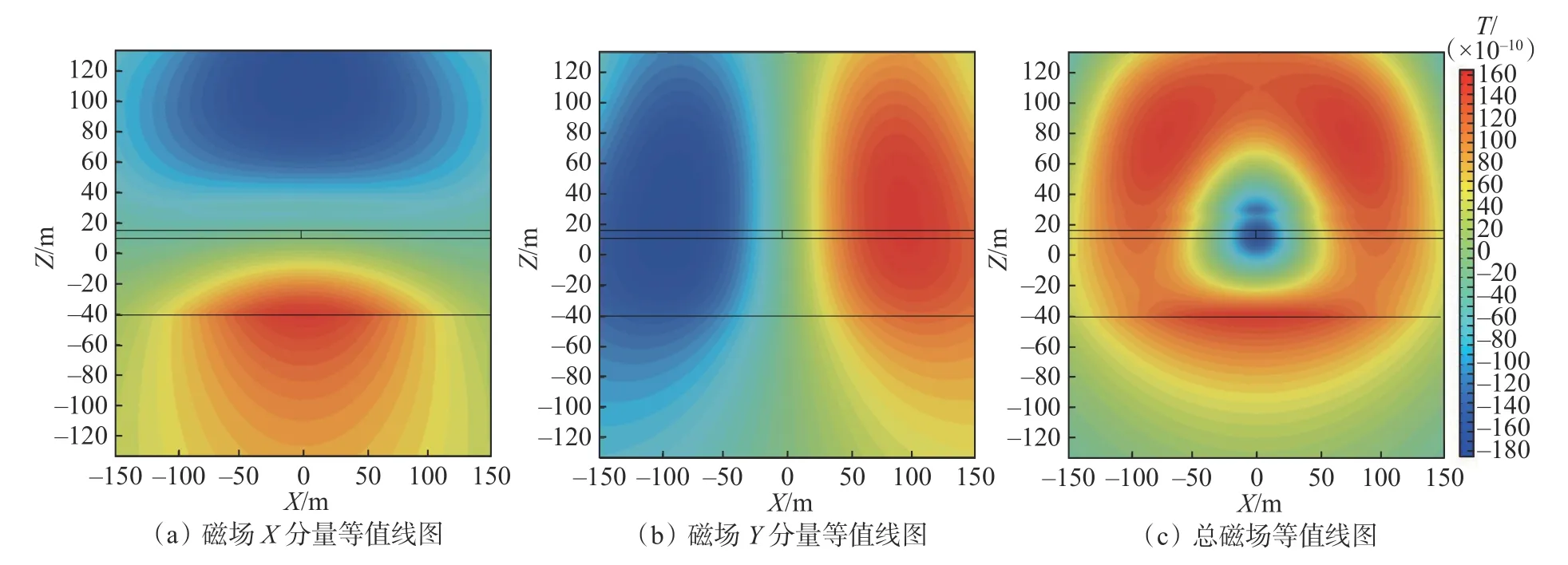
图4 无断层模型瞬变电磁0.10 ms 感应磁场等值线图Fig.4 The contour map of 0.10 ms induced magnetic field of transient electromagnetic without fault model
由图5 和图6 可知,就感应磁场等值线图整体而言,有断层模型的感应磁场的扩散规律与无断层模型相似,不同之处在于:①磁场X分量、Y分量以及总磁场的感应磁场等值线在断层所在位置发生了明显的畸变,等值线畸变的形状和范围与模型中断层的位置、走向和倾角吻合度较好;②总磁场等值线图在发射线圈附近出现一水平条带状等值线,结合模型图推断为砂岩与灰岩分界面的综合响应;③总磁场等值线图在Y=−40 m 处感应出一水平条带状正向磁场,这表明总磁场等值线能较好地刻画底板砂岩层与灰岩层的分界面。
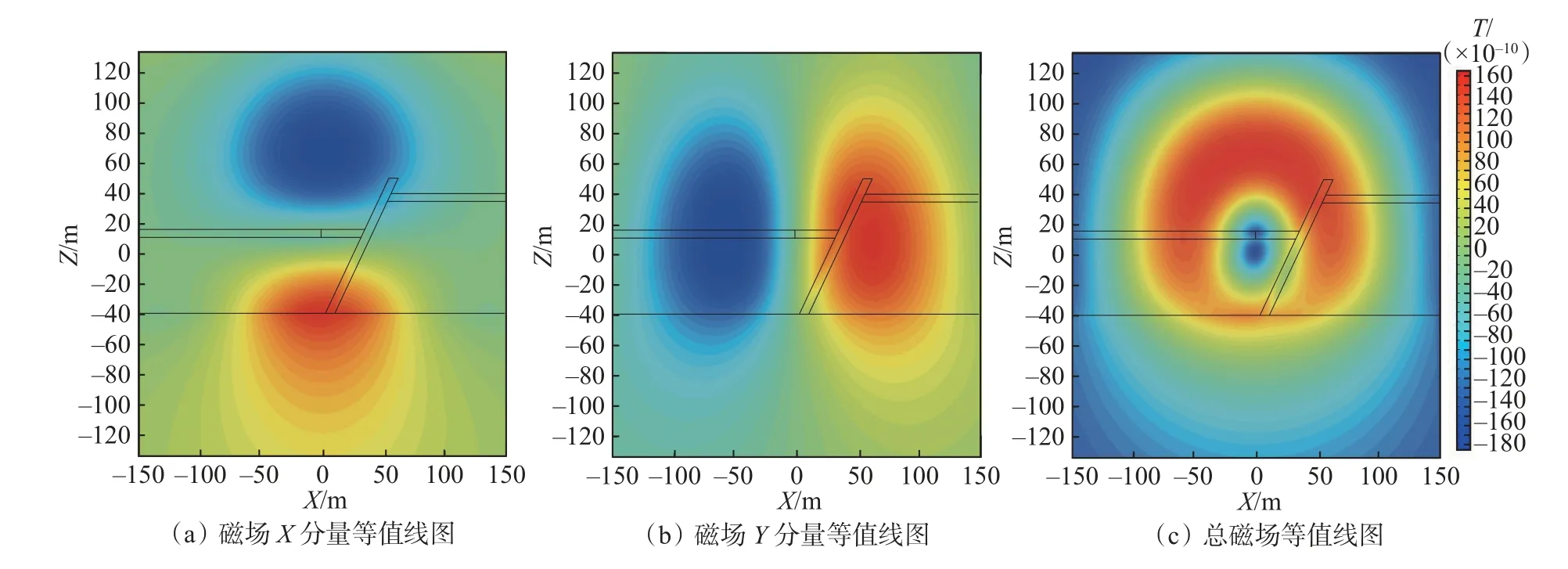
图5 有断层模型瞬变电磁0.06 ms 扩散磁场等值线图Fig.5 The contour map of 0.06 ms induced magnetic field of transient electromagnetic with fault model

图6 有断层模型瞬变电磁0.10 ms 扩散磁场等值线图Fig.6 The contour map of 0.10 ms induced magnetic field of transient electromagnetic with fault model
3.4 感应电动势及视电阻率响应特征
图7 为测点布置示意图,图8 为无断层模型和有断层模型不同测点位置的感应电动势对比曲线,横轴是采样时间,纵轴是感应电动势,分别计算了无断层模型和有断层模型中测点(0, 12.5)、(0, 10)、(0, 7.5)处的感应电动势,对比分析有无断层构造的瞬变电磁感应电动势响应特征。

图7 测点布置示意图Fig.7 Layout schematic diagram of measuring point

图8 有无断层模型的不同测点感应电动势响应图Fig.8 Emf responses of different measuring points with or without fault model
无断层模型不同测点位置的感应电动势如图8(a)所示。由图8(a)可知,随着测点位置的变化,感应电动势的幅值在采样早期增大,不同测点位置的感应电动势均出现一个向下凹的尖点响应,这表明感应电动势出现了极性反转现象,采样晚期的响应规律基本一致。
有断层模型不同测点位置的感应电动势如图8(b)所示。由图8(b)可知,随着测点位置与断层的距离减小,感应电动势的幅值在采样早期增大,不同测点位置的感应电动势均出现一个向下凹的尖点响应,这表明感应电动势出现了极性反转现象,尖点响应下凹的幅度相较无断层模型更大,推断这是由于断层影响导致。随着测点位置与断层之间的距离增加,尖点响应的最小幅值逐渐变小,采样晚期的响应规律基本一致。综上所述,不同测点位置的断层构造响应特征明显,响应规律存在差异,通过感应电动势出现的尖点响应特征能够判断工作面前方是否有断层构造。
设置了如图7 中的TEM 测线,分别将7 个测点的感应二次磁场值转换为全区视电阻率值,全区视电阻率计算方式参考了文献[19]中的方法,并得到了如图9 和图10 所示的无断层模型和有断层模型的视电阻率拟断面图。从图9 无断层模型的视电阻率成像结果可以看出,视电阻率值整体偏低,与煤系地层的电性特征较吻合,成像结果总体上与模型的电性特征近似。从图10 有断层模型的视电阻率成像结果可以看出,在X方向50 m 处显示一视电阻率突变的条带区域,且高阻电性响应明显,推断该处为断层发育带,与模型设置的断层基本一致,整体的成像结果符合模型的电性特征,表明正演结果准确可靠。

图9 无断层模型的视电阻率拟断面图Fig.9 Apparent resistivity pseudo section without fault model

图10 有断层模型的视电阻率拟断面图Fig.10 Apparent resistivity pseudo section with fault model
4 结 论
本文采用二维有限单元数值模拟技术,对比分析了高阻断层模型和无断层模型瞬变电磁场的扩散规律,得出结论如下所述。
1)基于二维有限单元法正演模拟技术揭示了高阻断层构造的瞬变电磁场响应规律,为井下瞬变电磁法超前探测的数据处理及资料解释提供了参考依据。
2)感应磁场等值线对高阻断层构造的响应规律明显,等值线畸变的形状和范围与模型中断层的位置、走向和倾角吻合度较好。总磁场等值线对巷道空气层、煤层的响应较好,对底板砂岩层与灰岩层(电阻率相差较大)的分界面刻画与模型基本一致。
3)对于高阻断层模型,随着测点位置与断层的距离减小,感应电动势响应幅值在采样早期增大,尖点响应的最小幅值逐渐变大,尖点响应下凹的幅度相较无断层模型更大,采样晚期的感应电动势响应规律基本一致,视电阻率成像结果能较好地反映高阻断层与煤系地层的电性特征,充分表明了正演结果准确可靠。

