基于改进遍布节理模型的岩石基坑开挖稳定性数值分析

曹国旭, 袁锐, 李元海*, 徐晓华, 王敦显

(1.广州地铁设计研究院股份有限公司, 广州 510030; 2.中国矿业大学深地工程智能建造与健康运维全国重点实验室, 徐州 221116;3.徐州地铁集团有限公司, 徐州 221000)

在岩石基坑工程设计及施工过程中,基坑围岩的力学特性是影响基坑开挖稳定性和支护结构安全性的重要因素,但实际基坑工程设计和计算会因施工地点地质条件的复杂性和围岩力学参数分布的离散性而将地质体按各向同性介质进行简化处理。但既有研究证明,层状岩体在不同层理倾角条件下,其变形和强度都表现出明显的各向异性,很大程度上影响对层状岩体力学行为的准确评价[1-2],层状岩体在平行于层理方向上力学性质比较相近,而在平行和垂直层理方向上的物理力学性质则差异较大。

随着城市地铁建设项目的日益增多,地铁车站基坑位于层状岩体中的工况愈发常见,而层状结构岩体在工程中容易发生滑坡、崩塌、碎落等灾害[3],对基坑开挖稳定性有着重要影响。沿用传统方法对该类岩石基坑的开挖稳定性和支护结构设计进行分析研究具有一定的局限性,因此,采用考虑层状岩体的各向异性方法,对修建于层状岩体中且含有高倾角外倾结构面这一特殊地质条件的基坑工程开挖稳定性进行研究十分必要。

当前国内外学者对岩石基坑设计施工和含外倾结构面边坡稳定性分析开展了一些相关研究,如熊超等[4]通过分析地质条件,结合FLAC3D进行数值模拟,研究了天生三桥岩溶景区深秀洞层状岩质基坑边坡变形破坏机制,并提出了以“框架锚索”和“肋柱锚杆”为主的分区治理方案。李杨秋[5]通过数值模拟分析了受缓倾岩层层面控制的超深岩质基坑支护设计方案及逆作法分步开挖对相邻地铁、公路隧道的影响。雷建海等[6]运用FLAC2D对层状岩质基坑壁的稳定性进行了模拟分析,发现软弱夹层的存在对坑壁岩体稳定性有较大影响,但只有当其力学参数未满足要求时,岩体才可能失稳滑动。罗福君等[7]采用FLAC3D内置的遍布节理模型描述层状岩体的各向异性特征,对岩体及节理面的稳定性影响参数进行强度折减并分析其与边坡安全系数的关系。贾帅等[8]采用遍布节理模型和摩尔-库伦模型分析了不同节理倾向、倾角与边坡角相互组合作用下对岩质边坡的影响,发现前者计算的边坡安全系数要小于后者,且边坡位移和速度变化更符合实际情况。上述研究有效推动了层状岩石基坑及含外倾结构面边坡的相关理论发展,但仍然存在以下问题:一是模拟时简单地将层状岩体考虑为各向同性介质,忽略了层状岩体变形和强度的各向异性。二是采用显式模拟方法,即采用实体单元对层面进行模拟,此种方法人为地设置了层面位置,降低了数值计算模型与实际工程的契合度。

此外,FLAC3D中传统的遍布节理模型虽然采用隐式方法考虑了结构面特性,但只能通过节理等效考虑岩体强度的各向异性,材料的变形性质仍然按照均质各向同性进行计算,无法真实反映层状岩体横观各向同性的变形特性[9]。新版本的横观各向同性弹性遍布节理模型无法考虑层状岩体的塑性流动特性,导致该模型应用范围受到较大限制[10]。

现依托徐州地铁3号线三环南路站车站岩石深基坑工程(灰岩地层),基于FLAC3D并对其内置的遍布节理模型进行二次开发,对岩体结构面进行隐式模拟,可有效避免显式建模的缺点,提高模型和实际工程的贴合度。得到考虑层状岩体变形和强度各向异性的横观各向同性弹塑性遍布节理模型,该模型能够完善FLAC3D中最新的横观各向同性弹性遍布节理模型,将岩体的塑性流动特性添加到该本构模型中,可拓展该模型的使用范围。基于该本构模型,对该基坑工程施工过程进行模拟分析,并进一步分析岩层倾角对基坑开挖稳定性的影响,以掌握不同倾角条件下基坑土体沉降、围护桩变形及基坑开挖完成后的安全系数变化规律,并针对软件无法获取安全系数分布的问题,基于软件内置语言编程,得到基坑围岩安全系数的分布云图,以期为含不同倾角外倾结构面岩石基坑的设计参数选取提供参考。

1 工程概况

1.1 车站概况

徐州地铁3号线三环南路站位于南三环路和北京路交叉口,沿北京路南北向布置,是徐州轨道交通3、4号线的换乘站,周边环境如图1所示。车站中部是同步实施的T形换乘节点。

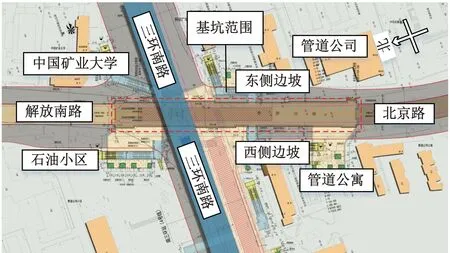
图1 南三环站的站位布置图Fig.1 Layout of Nansanhuan station

南三环站为两层岛式车站,站台为12 m宽,外包总长216.5 m。车站主体基坑长220.9 m,标准段宽25.7 m,深约24.5 m,中心里程处底板埋深约31 m。

1.2 工程地质条件

据勘察资料知,南三环站修建地发育有第四系全新统(Q4)、上更新统(Q3)地层,下伏基岩为奥陶系(Ο)灰岩,自上而下分为4个工程地质单元层及若干亚层,如表1所示。由于本站岩层倾向130°、倾角70°,岩层产状与基坑的位置关系如图2所示。其中,如图3所示,岩体结构面顺倾侧为基坑的西侧边坡,反倾侧则为基坑东侧边坡。导致基坑西侧高角度外倾节理发育的灰岩边坡存在顺层滑动、崩塌、倾倒和局部掉块等施工风险。

表1 南三环站地层结构Table 1 Stratum structure table of Nansanhuan station

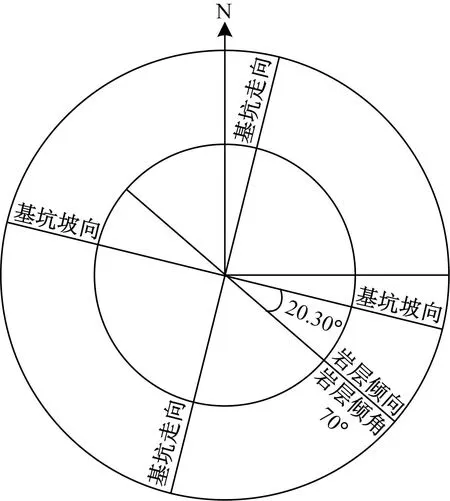
图2 岩层产状与基坑位置关系图Fig.2 Relationship between rock occurrence and foundation pit location

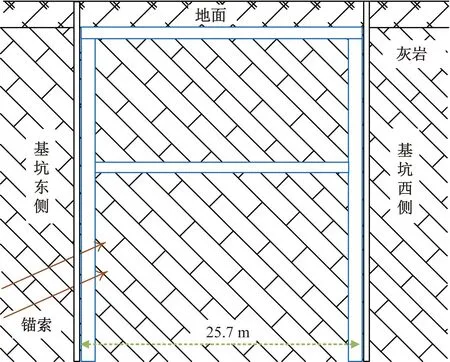
图3 基坑围护结构横断面示意图Fig.3 Schematic diagram of cross section of foundation pit retaining structure

1.3 围护结构设计

南三环站基坑围护结构采用围护桩+支撑(锚索)+喷锚支护。围护桩桩径为Φ1 000 mm,桩间距在换乘节点段为1.5 m,其他位置为2 m;冠梁为1 000 mm×1 000 mm,第一道支撑采用钢筋混凝土支撑,砼支撑ZC1尺寸为800 mm×1 000 mm,砼支撑ZC2为1 200 mm×1 000/800 mm,支撑纵梁ZCZL1为1 200 mm×1 000 mm;第二道支撑采用钢筋混凝土支撑,砼支撑ZC3为800 mm×800 mm,砼腰梁为1 000 mm×1 000 mm,基坑中部设有12根直径为1 200 mm的立柱桩兼抗拔桩,嵌岩深度6 m,立柱桩预埋环向钢板同第二道砼支撑、连系梁、剪刀撑连接;第二道支撑以下根据基坑埋深设有1～2道预应力锚索,一桩一锚,锚索腰梁采用钢筋混凝土腰梁,围护结构断面设计如图3所示。

2 横观各向同性弹性遍布节理模型改进

2.1 本构关系

对FLAC3D中的横观各向同性弹性遍布节理模型进行改进,引入塑性屈服准则,建立考虑岩体塑性流动的横观各向同性弹塑性遍布节理模型。该本构模型将层状岩石看作由横观各向同性弹塑性模型和遍布节理模型组成的复合体,且使横观各向同性面和遍布节理模型中的节理弱面相互平行,两个模型均采用带抗拉强度的摩尔-库伦本构模型,其中横观各向同性的强度准则按照各向同性考虑。

2.1.1 弹性本构关系

横观各向同性弹塑性体的本构关系在主应力空间(xyz-坐标系)中表述,而遍布节理本构模型在岩层层面的法向-切向应力空间(x′y′z′-坐标系)表述,如图4所示。横观各向同性体弹性变形满足胡克定律[11],局部坐标系下应力-应变关系为

(1)

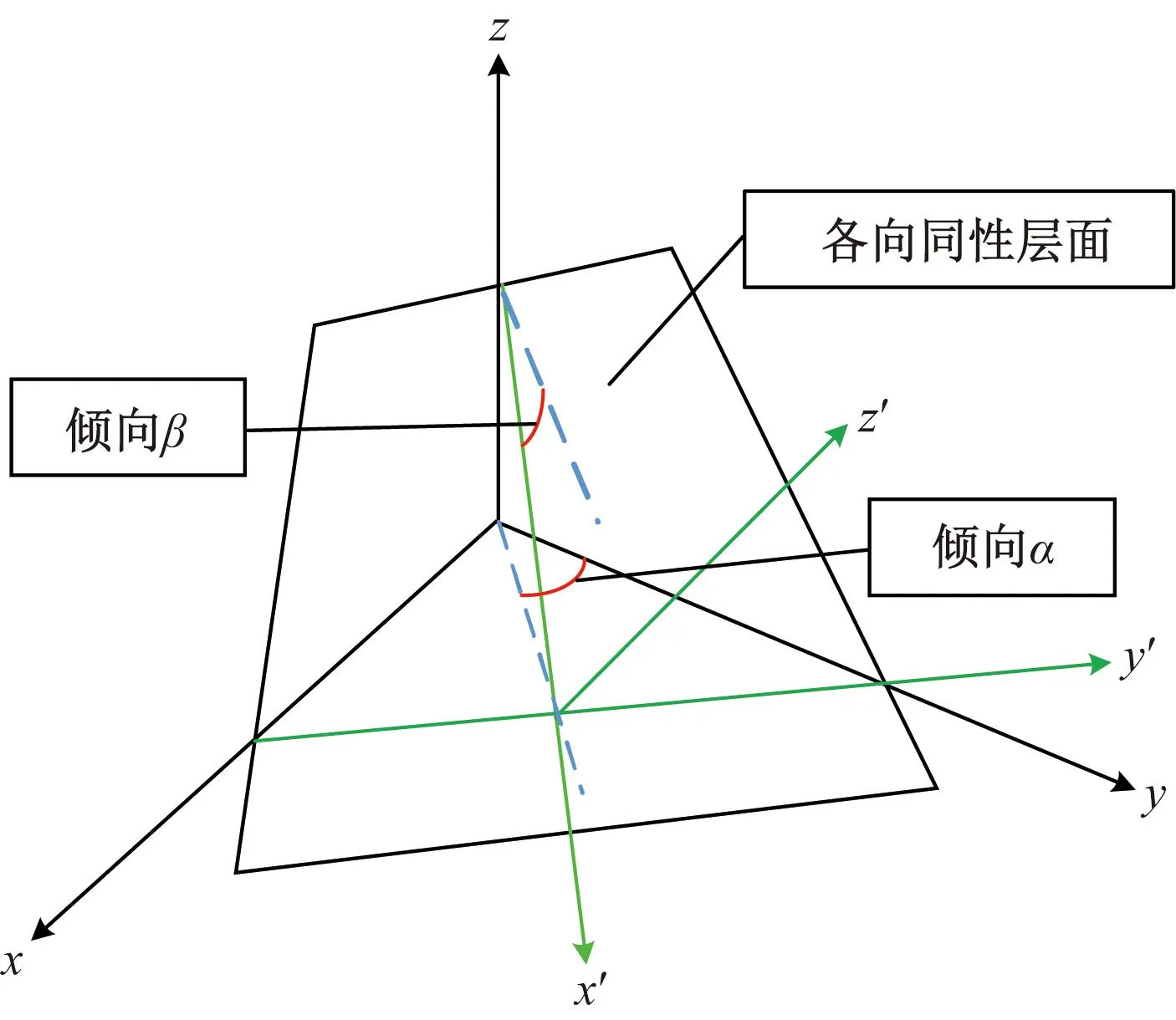
图4 整体与局部坐标系示意图Fig.4 Schematic diagram of global and local coordinate systems

式(1)中:E为各向同性平面的弹性模量;E′为各向同性平面法向方向的弹性模量;v为各向同性平面内的泊松比;v′为各向同性平面法向的泊松比;G为各向同性平面的剪切模量;G′各向同性平面法向的剪切模量。

由于两个模型组的坐标系选取存在差别,在经过弹性本构关系计算得到应力后需进行转换,将整体坐标系下的应力矩阵转换为局部坐标系下的应力矩阵,应力转换相关理论参考文献[10]。

2.1.2 屈服准则

横观各向同性弹塑性模型和遍布节理模型均采用带抗拉强度的摩尔-库伦本构模型,屈服准则由剪切屈服准则和拉伸屈服准则构成。模型的屈服函数和塑性势函数如表2所示。

表2 屈服函数和塑性势函数Table 2 Yield function and plastic potential function

2.2 程序实现过程

程序计算开始时由输入参数获取到整体坐标系下的弹性矩阵,假定为弹性应力计算,得到整体坐标系下的应力矩阵,并使用应力转换矩阵将应力转换为局部坐标系下的应力,按照表2中的节理弱面的屈服函数分别进行节理弱面的张拉或剪切屈服破坏判别。如果节理面发生破坏,则在局部坐标系下对应力矩阵进行应力修正,并在应力修正后使用应力转换矩阵将局部坐标系下的应力转换为整体坐标系下的应力,如未发生破坏,则直接进行应力转换,然后按照表2中岩石的屈服函数对岩石的拉伸或剪切屈服破坏分别进行判别,若岩石发生剪切或拉伸破坏,则对应力进行修正。重复上述过程,直至计算结束。具体过程如图5所示。按照上述步骤,在VC++环境中完成该本构模型的开发后,将模型动态链接到FLAC3D中即可用于计算。

图5 程序实现流程图Fig.5 Program implementation flow chart

3 有限差分数值分析

3.1 数值计算模型

采用FLAC3D对基坑的开挖过程进行分析。根据工程经验及有限元计算结果,基坑开挖影响宽度为深度的3～4倍,影响深度为深度的2～4倍,选取基坑开挖最深段建立数值模型,模型长度为52 m,宽度为227 m,深度方向为100 m,如图6所示。西侧边坡内岩层倾角为外倾,东侧边坡内岩层倾角为反倾。模型的左右及前后边界施加水平方向位移约束,底部边界施加竖直方向的位移约束。

3.2 数值计算条件

计算区域内灰岩采用改进遍布节理模型,其他岩土材料采用莫尔-库仑模型,岩土层力学参数依据现场实验及实验室的测试结果确定。冠梁、砼支撑、桩和锚杆等围护支护结构采用结构单元模拟,各结构单元的力学参数如表3所示。

表3 支护结构力学参数表Table 3 Supporting structure mechanics parameter table

钻孔灌注排桩因桩间距较小,同时采用了冠梁、腰梁及喷锚使其实际上是一个连续的整体,且需要考虑其与桩间土的作用,因此采用FLAC3D中的Liner单元模拟[12],砼支撑、冠梁、腰梁及锚索腰梁采用Beam单元模拟,预应力锚索采用Cable单元模拟。

3.3 本构模型各向异性评价

为验证模型的正确性并对其各向异性特征进行评价,采用该模型和FLAC3D自带的遍布节理模型进行了横观各向同性面倾角为70°时的单轴压缩数值模拟实验。数值实验模型为标准圆柱体模型(Φ50 mm×100 mm),受力状态为理想单轴受压应力状态,灰岩单轴压缩数值实验的力学参数如表4所示。为保证模拟过程完全相同,在模型的上下表面采用位移控制的方式进行加载,设置加载速度为2×10-3mm/步,其他面均为自由边界,并计算相同的步数,得到轴向应力与轴向应变的关系曲线如图7所示。

表4 单轴压缩数值实验岩石力学参数表Table 4 Table of rock mechanics parameters for uniaxial compression numerical experiment

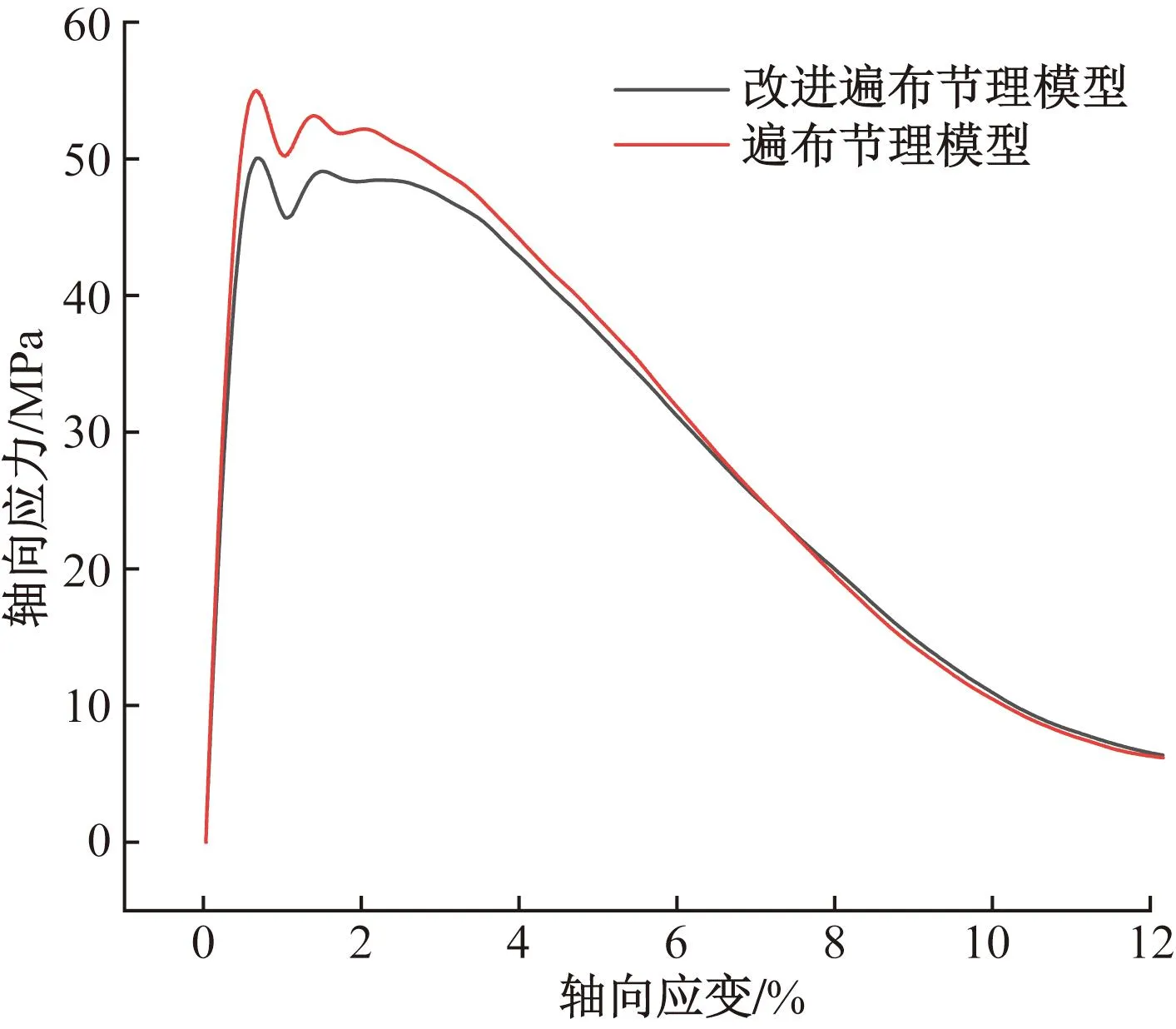
图7 70°倾角下轴向应力-轴向应变曲线Fig.7 Axial stress-axial strain curve at 70° inclination

由图7可知,遍布节理模型改进前后的应力-应变曲线变化规律相似,但由于改进后模型考虑了各向同性平面内及其垂直方向上的变形各向异性,在线弹性阶段和相同的轴向应力条件下,轴向应变较改进前的模型更大,在靠近峰值应力附近,两个模型计算的应变差异更加的明显。上述结果表明改进遍布节理模型能更好地反映试样的变形各向异性。

图8为标准尺寸模型中间断面的竖向位移(正值代表向上,负值代表向下)云图。

图8 70°倾角下试件竖向位移云图Fig.8 Vertical displacement contour of specimen under 70° inclination angle

由图8可知,改进前后的模型计算得到的竖向位移均呈层状分布,在试样的顶面和底面,由于设置有相同的加载速度,云图层面接近水平,在试样中部位移云图层面倾角约为70°,试样的右上角(A和D区域)及左下角(C和F区域)一定范围的竖向变形较大。对比分析两种模型计算结果发现,在试样右上角及左下角一定范围内的相同位置处,改进遍布节理模型因考虑了变形的各向异性,计算的竖向位移较遍布节理模型更大,且改进遍布节理模型产生竖向变形的范围更大(区域DF较AC大)。

4 计算结果

4.1 监测-模拟数据对比分析

南三环站施工监测项目主要包括围护结构变形、地表沉降和支撑结构轴力等。采用监测数据来检验数值模型的可靠性。

图9是地面沉降监测值与数值模拟值的对比图。通过对比可以看出,监测最大值约为9.8 mm,模拟最大值约为9.2 mm,地面沉降监测值分布在-9.8～0.44 mm,模拟值分布于-9.2～-1 mm,地面沉降监测数据与模拟数据的分布范围基本一致,差异较小,表明数值模拟的地面沉降数据基本能反映实际工程中的地面沉降情况。

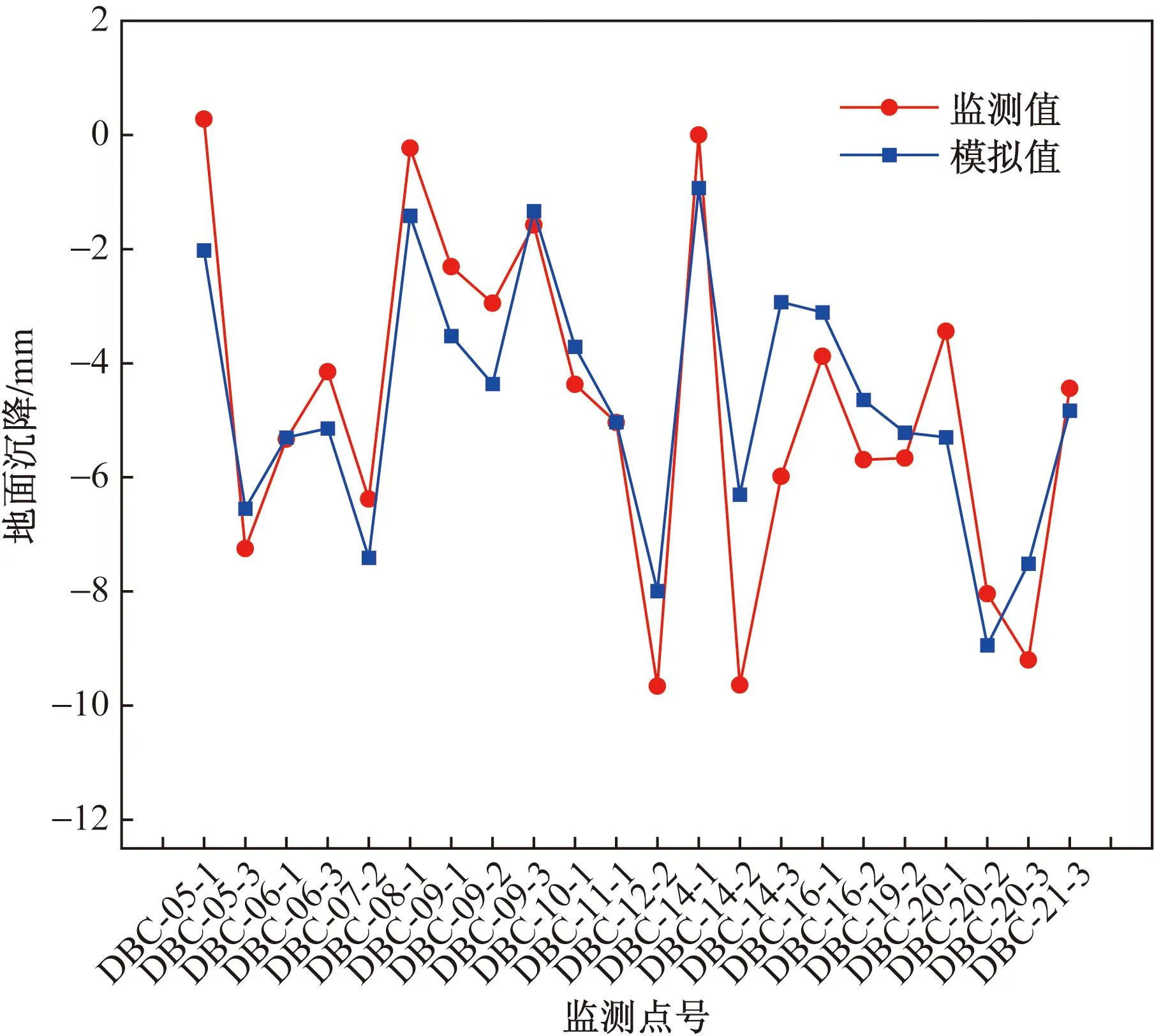
图9 地面沉降监测值与模拟值对比图Fig.9 Comparison chart of ground subsidence monitoring value and simulation value

图10为围护桩ZQT-07水平位移监测值与模拟值对比图,其中负值表示朝向坑内变形,正值表示朝向坑外变形。通过对比发现,模拟值与监测值的趋势基本相同,两者均为类“弓形”变形。围护桩水平位移监测最大值约为9 mm,出现位置为围护桩埋深为13 m附近,模拟值的最大值约为8.6 mm,出现位置为围护桩埋深为15 m附近,表明数值模拟的围护桩水平位移数据基本能反映实际工程中的围护桩水平位移情况。

图10 围护桩ZQT-07水平位移监测值与模拟值对比图Fig.10 Comparison diagram of horizontal displacement monitoring value and simulated value of retaining pile ZQT-07

4.2 岩层倾角影响分析

为研究岩层倾角对基坑开挖稳定性的影响,在保证岩土层力学参数、支护结构设计和计算过程完全相同的条件下,仅改变岩层倾角,分别进行不同倾角条件下基坑开挖模拟并进行对比分析。

4.2.1 地面沉降分析

基坑外侧的沉降分布情况对于周边建筑物的变形控制以及基坑工程的安全施工具有重要意义。为定量分析岩层倾角对于基坑外侧地表沉降的影响规律,提取基坑西侧和东侧的地表沉降数据进行分析,如图11所示。由于岩体结构面的存在,各倾角下东西侧地表的沉降分布及最大沉降量均呈现明显差异。当岩层倾角为30°～80°时,西侧地表均呈现为凹槽式沉降:基坑边墙处出现小范围的隆起,之后向坑外处产生逐渐增大的沉降现象,并在距基坑边墙一定距离处出现最大沉降点,随后地表沉降值逐渐减小直至影响边界。当岩层倾角为0°、10°、20°及90°时,西侧地表均出现了轻微的隆起变形,出现最大隆起点的位置为靠近基坑边墙处,这是由于改进横观各向同性弹塑性遍布节理模型的屈服准则使用的是摩尔-库伦准则。在计算过程中,当基坑边坡岩土体达到屈服后,模型计算的剪应变为无限增大的弹塑性变形,体应变为无限增大的体胀变形,地表变形表现为隆起变形。此外,岩层倾角对西侧地面最大沉降量有较明显的影响,当岩层倾角为40°～80°时,随岩层倾角的增大西侧地面沉降最大值满足先增后减的规律,当岩层倾角为50°时西侧地表的沉降量最大,为12.28 mm。当岩层倾角为40°～80°时,东侧地表呈现为凹槽型沉降,最大沉降量同样满足随倾角的增大先增后减的规律,最大沉降量出现在岩层倾角为50°时,为11.5 mm。

图11 不同岩层倾角下地面沉降曲线Fig.11 Ground settlement curve under different rock stratum inclinations

4.2.2 桩位移分析

图12为不同岩层倾角条件下基坑西侧和东侧围护桩的水平位移曲线。

图12 不同岩层倾角下基坑西侧围护桩水平位移曲线Fig.12 Horizontal displacement curves of retaining piles under different rock inclination angles

可以看出,各岩层倾角下,东西侧围护桩的变形模式基本相同,呈现一种类“弓形”。最大水平变形出现在桩体中部,桩顶及桩底处变形较小,这种“弓形”变形特征与既有研究结果一致。对于西侧围护桩,当岩层倾角在40°～70°范围时,围护桩水平位移最大值在8～14 mm范围内,其他倾角下,围护桩的水平位移最大值在2～5 mm范围内。从量值范围上看,倾角在40°～70°范围内时围护桩水平位移最大值较其他倾角下有明显增大。对于东侧围护桩,当岩层倾角为0°～30°倾角时,围护桩水平位移最大值集中在2～3 mm范围内,当倾角为40°～70°时,围护桩水平位移最大值在4.1～10 mm范围内,而当倾角为80°～90°时,岩层接近直立,此时桩水平位移较小。对比地面沉降和桩水平位移,在岩层倾角为40°～70°范围内两者具有较好的对应关系,东西侧地面沉降和围护桩位移得最大值均出现在50°。

4.2.3 最大剪应力分析

为定量分析基坑开挖完成后西侧边坡内部岩体的最大剪应力,获得埋深为28 m时,距离基坑西侧开挖面不同距离处的最大剪应力曲线如图13所示。

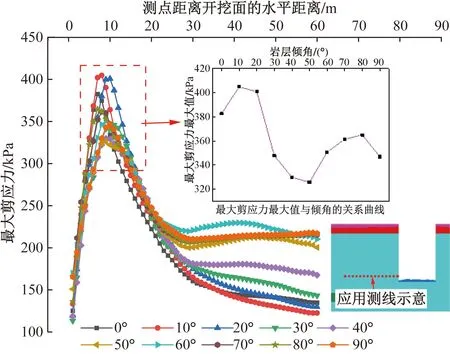
图13 基坑西侧测线最大剪应力分布曲线Fig.13 The maximum shear stress distribution curve of the survey line on the west side of the foundation pit

可以看出,同一埋深处而不同岩层倾角下的西侧边坡内岩体的最大剪应力分布满足随着与开挖面距离的增加先增后减最终趋于稳定的规律。在与开挖面的距离大于30 m后,围岩最大剪应力趋于稳定。各倾角下最大剪应力最大值均出现在距离开挖面6～10 m范围内,最大剪应力集中处岩体更易发生破坏。根据前文分析,该范围内西侧边坡地面沉降量逐渐达到最大。岩层倾角为0°～20°时,最大剪应力值较大,当岩层倾角为30°时,最大剪应力值显著降低。最大剪应力最大值中的最小值出现在岩层倾角为50°时,为325.8 kPa。

4.2.4 安全系数分析

强度折减法定义安全系数为岩土体的实际抗剪强度与临界破坏时经折减后的抗剪强度的比值[13-14]。为分析不同倾角下基坑开挖完成后边坡岩体的稳定性,采用强度折减法计算得到各倾角下基坑边坡的安全系数如图14所示。FLAC3D中模型的安全系数计算包含多次折减计算步,在折减计算步之间,采用二分法逐渐调整折减系数,折减系数的取值精度越高,计算结果越正确。

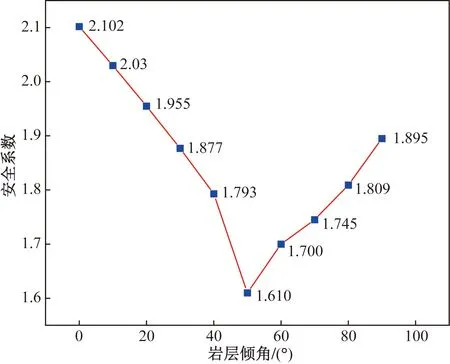
图14 不同岩层倾角下基坑安全系数Fig.14 Safety factors of foundation pits under different rock inclination angles

安全系数分布整体呈“V”字形分布,即:当岩层倾角为0°～50°时,随着岩层倾角的增大,基坑边坡的安全系数逐渐降低,当岩层倾角为50°～90°时,随岩层倾角的增大,基坑边坡的安全系数逐渐增大,在岩层倾角为50°时最小,为1.61。随着岩层倾角的增大,岩层由近水平状逐渐改变为近直立状,近直立岩层较近水平岩层的安全系数更小,表明其稳定性更低。

部分倾角下基坑围岩的安全系数分布云图如图15所示。当岩层为近水平(20°)岩层时,基坑西侧边坡潜在滑动面形式不受岩层倾角影响,形式为圆弧形,如图15(a)所示。当岩层倾角为50°时,基坑西侧边坡的潜在滑动面与岩层层面重合,为沿着岩层层面的直线型滑动面,如图15(b)所示。当岩层倾角为80°时,基坑西侧边坡上半部分岩体的潜在滑动面与岩层的层面基本重合,在靠近西侧坑底附近为圆弧形滑动面,基坑西侧边坡的潜在滑动面为直线形和圆弧形滑动面组合滑动面,如图15(c)所示。由于基坑东侧边坡为反倾边坡,其潜在滑动面均为圆弧形,与岩层倾角无明显关系。

图15 不同岩层倾角下基坑围岩安全系数云图Fig.15 Contour of safety factor of foundation pit under different rock layer inclination angles

4.3 桩间距优化

基于强度折减法的基坑安全系数计算结果表明,该基坑围护结构原设计具有较大的优化空间。因此,选择基坑最深段模型,从调整围护桩间距方面开展数值模拟研究。基坑最深段围护桩的间距T设计值为1.5 m,在保持其他支护结构设计和力学参数完全相同前提下,分别取T、2T和3T的桩间距进行对比分析。

图16为不同围护桩间距下的基坑开挖完成时的地面沉降曲线图。可以看出,随着围护桩间距的增大,东西侧边坡地表的最大沉降量均在逐渐增大。对于西侧边坡,当桩间距为2T时,地表最大沉降量约为T时的1.3倍,当桩间距扩大为3T时,地表最大沉降量约为T时的1.63倍。对于东侧边坡,当桩间距扩大为2T时,地表最大沉降量约为T时的1.12倍,当桩间距扩大为3T时,地表最大沉降量约为T时的1.37倍。两侧基坑边坡周围的地表沉降值均小于30 mm的控制基准值。结果表明,当前设计的岩石基坑围护桩的间距可以增大到1～2倍,在确保安全的前提下,对于加快施工工期和降低工程造价具有重要意义。

图16 不同围护桩间距下地面沉降曲线Fig.16 Ground settlement curve under different spacing of retaining piles

根据该围护桩的桩间距优化分析结果,同站换乘的4号线南三环路站基坑围护桩在设计施工时的桩间距由3号线的1.5 m扩大到2.5 m,实际增大约0.7倍。施工监测表明,围护桩间距扩大后的基坑周围地表最大沉降约为13 mm,满足地表变形安全控制要求。

5 结论

对FLAC3D中既有的横观各向同性弹性遍布节理模型进行了改进,基于改进后的本构模型模拟分析了0°～90°岩层倾角条件下基坑及其围护桩的变形规律,并提出了围护桩间距优化建议。

(1)东西侧地表最大沉降值均出现在岩层倾角为50°时。当岩层倾角为40°～80°时,东西侧地表呈现为凹槽式沉降,最大沉降量均满足随着倾角的增大先增大后减小的规律。

(2)强度折减法计算结果表明,在完全相同的支护设计条件下,在岩层倾角为50°时,基坑开挖完成后的安全系数最低为1.61,该结果与围护桩最大位移,地面沉降最大值及剪应力最大值具有较好的对应关系。

(3)随岩层倾角的增加,基坑西侧边坡的潜在滑动面形式由圆弧形滑动面(0°～20°)转变为沿着层面的直线形滑动面(30°～60°),再转变为直线形与圆弧形组成的组合型滑动面(70°～80°),最后转变为圆弧形滑动面(90°),东侧边坡的潜在滑动面始终为圆弧形滑动面。

(4)依托工程当前设计的围护桩间距对于工程的岩石基坑条件较为保守。计算表明围护桩间距可以增大到1～2倍,由于工程设计中倾向于更高的安全系数,后续邻近新建车站基坑的围护桩据此将间距实际增大约0.7倍,地表沉降监测表明满足施工安全要求,对缩短工期和降低造价具有参考价值。