道路网络多阶段抗灾能力优化模型构建与应用

刘鹏，路庆昌，秦汉，崔欣

(1.长安大学 电子与控制工程学院，陕西 西安 710064；2.大连海事大学 航运经济与管理学院，辽宁 大连 116026)

重大灾害下道路交通网络灾害应对能力优化是一项多阶段、长期性的系统工程，包括灾前的准备阶段和灾后的恢复阶段[1].重大灾害下路网大范围受损会造成大量路段和节点的不可达，造成大量恢复资源无法抵达受损路段，严重阻碍灾后路网的高效恢复[2-3].道路交通网络抗灾能力的优化，不仅取决于灾前准备阶段的恢复资源的选址布设，也取决于灾后恢复阶段恢复资源的排程调度.

应急工作站点选址优化问题常被建模为覆盖问题，通过优化应急救援设施的布设位置和数量，以覆盖更多、更重要的路段和节点[4-7].Guo 等[5]提出协作覆盖模型，研究多交通方式联运网络中应急救援设施的选址策略.交通网络恢复决策优化问题常被建模为选择问题或排程问题[8]，通过确定待修复路段的集合和修复时序，提升路网抗灾能力.其中，应急救援设施的排程调度优化得到了广泛的研究和讨论[8-9].Li 等[8]在恢复决策建模中综合选择问题与排程问题，获得应急恢复阶段路段恢复持续时间不确定情况下的待修复路段集合及修复时序.Maya-Duque 等[10-12]研究应急救援设施排程调度和路径决策综合优化问题，考虑受损路段可达性对路网恢复决策的影响.Maya-Duque 等[10-11]提出考虑路径决策的路网恢复优化模型，研究假设应急救援设施仅能够修复路网中可达的受损路段.

除了由恢复工作组和恢复设备组成的应急救援设施，灾后恢复工作的高效开展还需要后勤保障资源的支持，包括水泥、钢材和燃油等消耗性资源[13].2008—2011 年，汶川地震灾区的水泥和钢铁供应量分别为12 300 万t 和1 080 万t[14].Yan 等[13]研究后勤保障资源的最优调度问题，以最小化车辆运营成本和后勤保障资源调度成本为优化目标.Li 等[15]构建应急救援设施和后勤保障资源的综合调度优化模型，定性建模了两者相互协作关系对路网恢复的影响.然而，应急救援设施和后勤保障资源在耗尽性、恢复作用和运输方式上有显著差异.应急救援设施是非消耗性资源，决定了路网恢复的速度；后勤保障资源是消耗性资源，影响路网恢复程度[16].为了尽可能降低运输成本，在最短时间内覆盖更多的受损路段，应急救援设施在完成一条路段的恢复后会直接前往下一条受损路段进行工作[17].后勤保障资源所需的数量巨大，不能一次性跟随应急救援设施全部运往受损路段，而是需要单独从应急工作站点运往受损路段[15].

综上所述，道路交通网络多阶段抗灾决策优化依赖于后勤保障资源和应急救援设施的相互协作.当前的研究大多集中在应急救援设施多阶段优化模型的构建上，忽略了后勤保障资源的多阶段优化.Hackl 等[16]研究考虑灾后恢复阶段2 类资源的综合建模，但是未能有效地刻画两者的特点，也未能定量建模两者对路段恢复的影响和相互协作关系.本文提出混合整数3 层规划模型.上层模型用于确定应急工作站点的灾前选址布设.中层模型通过计算应急救援设施路径流和后勤保障资源路径流，获得不同时间步下的路网恢复状况.下层模型用于获得不同时间步下的用户出行情况.基于贵州省区域高速公路网络，验证了本文模型的有效性和优越性.

1 研究方法

1.1 模型构建

1.1.1 基本假设 1）重大灾害后受损路段无法双向通行，采用无向网络G(N,A) 表示道路网络.其中N为节点集合，i∈N；A为路段集合，a∈A.决策优化模型适用于灾害事件下各类道路交通网络的多阶段抗灾决策优化.2）应急救援设施包含救援工作组和救援设备，决定了路段的恢复速度 ρE，即单位数量应急救援设施能够在单位时间内恢复的路段容量.3）后勤保障资源为砂岩、水泥、沥青和混凝土等各类恢复材料，决定了路段的恢复程度 ρM，即单位数量的后勤保障资源能够恢复的路段容量.4）后勤保障资源、应急救援设施和用户交通流的分配以固定单位步长 Δt进行，不考虑步长内的动态变化.5）在灾后恢复过程中，路网中OD 对w间的出行需求qw保持不变[18].6）应急工作站点无法存放路网完全恢复所需的全部后勤保障资源，每一时间步下每个工作站点依据其存储能力，更新该站点可用后勤保障资源的数量.

1.1.2 优化目标 重大灾害下的路网抗灾成本包括灾前应急工作站点布设成本和灾后路网恢复成本[16-17].灾后恢复成本包括与灾后恢复决策相关的直接成本和与用户出行相关的间接成本.其中，直接成本主要指与灾后恢复决策相关的各项开支，如路段重建和费用物资运输费用[16].间接成本为与用户出行相关的费用.本文的优化对象为受损路网恢复到灾前状态的全恢复过程，恢复决策无法降低包括路段重建在内的固定费用，而合理的物资调配路径规划可以有效地降低物资运输成本.与后勤保障资源相比，路网恢复所需的应急救援设施数量小得多.由于应急救援设施无须返回应急工作站点，直接前往下一受损路段进行作业，运输路径的长度相对更小.应急救援设施的运输成本相对很小，甚至可以忽略不计.选取后勤保障资源运输成本PM为灾后路网恢复的直接成本.

式中：T为时间步t的集合，t∈T；N(i) 为节点i的相邻节点集合，N(i)⊆N；cM为后勤保障资源运输成本的加权因子；为中层模型决策变量，表示灾后t时间步节点i流向节点j的用于恢复路段a的后勤保障资源数量；为灾后t时间步路段a的时间阻抗.

重大灾害后，路网中存在大量的不连通OD，恢复路网连通性是路网恢复决策的首要任务，以保障应急救援和灾后重建工作的顺利进行.选取未满足出行需求惩罚成本PW，度量网络连通性损失造成的路网恢复间接成本.

式中：cW为未满足出行需求的加权因子；W为OD 对w的集合，w∈W；为0-1 变量，表示灾后t时间步 ODw的运营状态，若OD 正常运营，则=1，否则=0.

除了大量的不连通OD，路段受损也会造成交通拥堵和出行绕行，导致连通OD 出行成本的增加.为了更好地评估重大灾害对人们出行的影响，选取连通OD 出行阻抗增加惩罚成本PZ，度量路网恢复的另一间接成本.

1.1.3 决策优化模型 建立的道路网络多阶段抗灾能力优化模型为混合整数3 层规划模型，其中上层模型为应急工作站点布设决策优化问题，中层模型为最小费用流问题[19]，下层模型为用户均衡配流模型.模型的作用机制如下：上层模型决策变量输入到中层模型，决定灾前各节点的应急救援设施布设数量和后勤保障资源存放能力，影响灾后各时间步的应急救援设施流和后勤保障资源流.根据中层模型，计算获得不同时间步下各受损路段的恢复情况，传递到下层模型.基于不同时间步下的路网运营状态，下层模型通过求解用户均衡配流模型，计算得到各时间步下所有OD 的行程时间阻抗和运营状态，并传递回中层模型.利用中层模型计算得到灾后路网加权总恢复成本，并输入到上层模型，以便上层模型计算出优化目标路网抗灾成本.

上层模型如下：

式中：P为加权总恢复成本；xi,u为上层模型决策变量，表示若类型为u的恢复工作站点布设在节点i，则xi,u=1，否则xi,u=0 ；X为xi,u的集合；bu为u类型应急工作站点的布设成本；B为应急工作站点的最大布设数量；U为应急工作站点类型的集合.

式（4）为上层模型目标函数，最小化路网恢复成本与工作站点布设成本之和.式（5）为应急工作站点的布设数量约束.

中层模型如下：

式（7）为中层模型的目标函数，旨在最小化灾后总加权恢复成本，其中加权系数cM、cW和cZ将后勤保障资源的运输成本、未满足出行需求和用户出行阻抗增量转换为相同的成本量纲.式（8）表示各节点向某一路段提供的后勤保障资源数量为该节点流向该路段的后勤保障资源净流出量.式（9）表示后勤保障资源只能通过正常运营的路段运输，且数量不超过路网完全恢复所需的全部后勤保障资源数量，其中a′:i→j表示a′为节点i与节点j间的路段.式（10）表示各节点能够提供的后勤保障资源数量不超过该节点存储能力.式（11）约束灾后恢复过程中提供给各受损路段的后勤保障资源所能恢复路段容量取决于该路段的容量、长度和受损程度.式（12）约束了灾害发生时间步t=1 时各节点可用的应急救援设施数量.式（13）表示灾后t＞1 时各节点可用的应急救援设施数量为流入该节点的数量与该节点上一时间步可用数量的总和.式（14）表示各节点向外提供的应急救援设施数量不超过该节点的可用数量.式（15）表示应急救援设施只能通过正常运营的路段运输，且数量不超过路网布设的全部应急救援设施数量.式（16）表示灾后恢复过程中提供给各受损路段的应急救援设施所能恢复路段容量取决于该路段的容量、长度和受损程度.式（17）表示灾害发生时间步t=1 时各路段受损程度与运营状态间的对应关系.式（18）表示灾后t＞1 时各路段受损程度与运营状态间的对应关系.式（19）表示受损路段的容量恢复量不超过该路段的受损容量.式（20）表示各受损路段的容量恢复量为该路段可用应急救援设施恢复量和可用后勤保障资源恢复量的最小值.式（21）表示当所有路段都正常运营时恢复结束.式（22）～（25）为中层模型各变量的取值约束.

下层模型：

式（26）～（29）为带时间序列的用户均衡配流问题[9].式（30）表示路段运营状态和OD 运营状态间的关系.均衡状态下所有OD 对间的连通路径有着相同的行程时间阻抗，因此式（30）中的路径可以取OD 对间的任意一条最短路径[20].式（31）用于计算各路段的行程时间阻抗.式（32）表示路段行程时间阻抗和OD 间行程时间阻抗的对应关系.式（33）约束 ζw,p,a,t为0-1 变量.

1.1.4 模型分析 现有道路交通网络多阶段综合优化问题多关注应急救援设施的布设和调度优化问题，忽略了后勤保障资源的多阶段优化.尽管有研究考虑了后勤保障资源与应急救援设施的综合优化，但未能区分两者间的特点差异和定量建模两者间的相互协作关系.通过构建不同的流量守恒约束，区分两者在耗尽性和运输方式上的差异.式（8）、（10）约束后勤保障资源只能从应急工作站点分发，且数量会因路段的恢复而减少，而式（12）～（14）保障应急救援设施能够在完成一条路段的恢复工作后直接抵达下一条受损路段，且数量不会发生变化.模型通过式（11）、（16）和（20）区分了两者恢复作用的差异，后勤保障资源决定了路段恢复程度，应急救援设施决定了路段恢复速度.基于“瓶颈效应”的思想，该模型通过式（20）定量建模了两者间的相互协作关系.

1.2 算法设计

构建的3 层模型包括上层模型的选址问题、中层模型的后勤保障资源与应急救援设施的路径决策和路网恢复排程决策综合优化问题、下层模型的用户均衡配流问题.相较于具有NP-hard 特性的应急救援设施调配路径决策优化问题[10]，该模型考虑了应急工作站点选址和后勤保障资源调配路径决策，定量建模了应急救援设施和后勤保障资源间的协作关系，使得模型的求解难度更大.采用双层遗传算法求解上层模型和中层模型，基于Frank-Wolfe 算法求解下层模型，算法流程如图1 所示.

1.2.1 染色体编码 上层遗传算法采用二进制编码方法，对应急工作站点的选址进行编码.染色体的长度为路网中的节点数目，每一位依次用于判断路网中的相应节点是否被选为工作站点.其中，数字“1”表示选择该站点为工作站点，数字“0”则相反.例如，“001100”表示在染色体第3 位和第4 位对应节点布设应急救援设施和后勤保障资源.下层遗传算法使用基于优先度的整数编码方法.染色体的长度为路网中受损路段的数目，每一位表示受损路段的恢复优先级，优先级越高的路段越被优先分配应急救援设施和后勤保障资源，如“1 432 576”表示染色体第1 位所对应的路段将优先被分配应急救援设施和后勤保障资源.下一节将详细描述下层遗传算法的解码过程，具体流程如图2 所示.

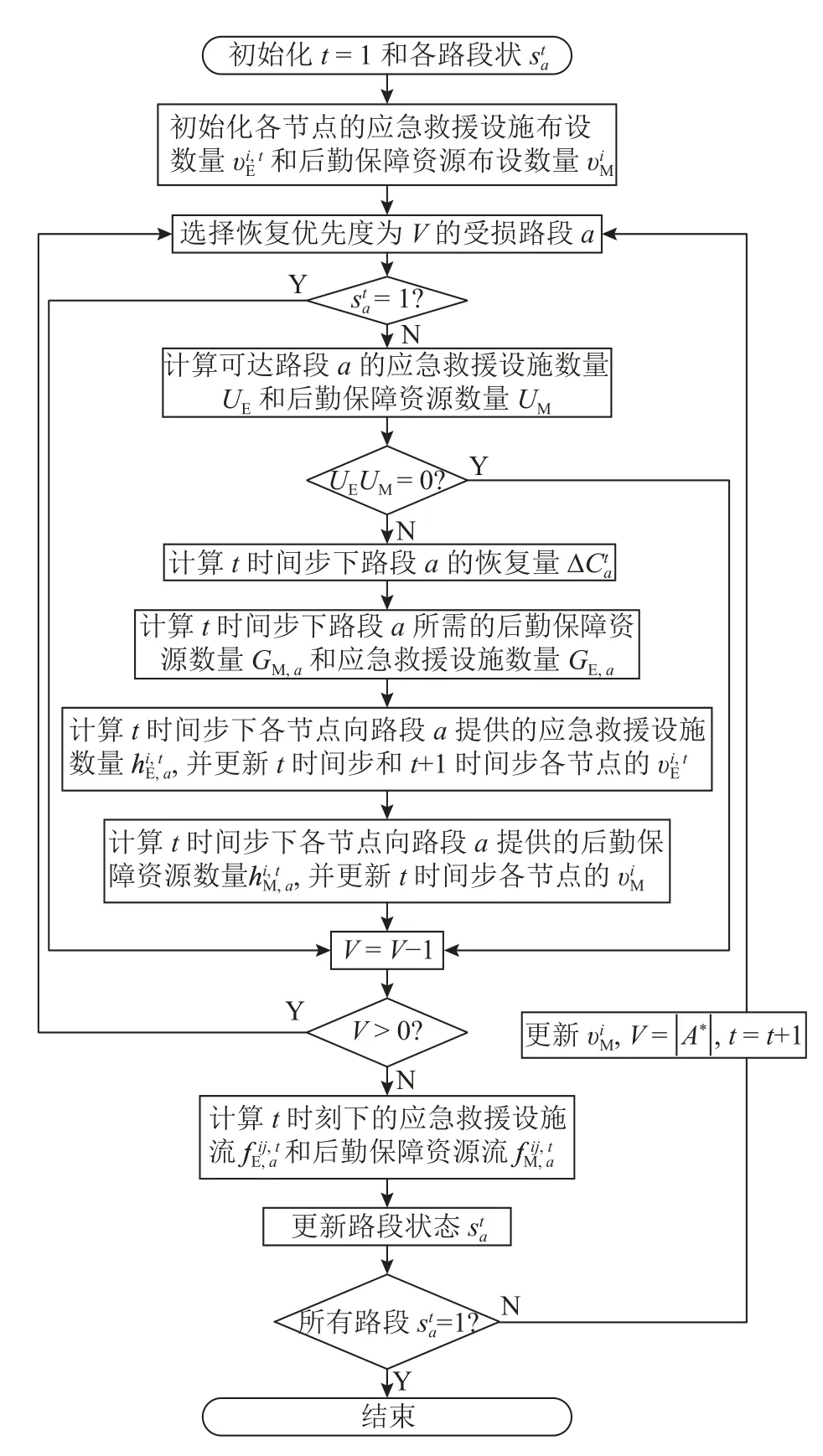
图2 下层遗传算法解码过程的流程图Fig.2 Flowchart of decoding process for lower-level genetic algorithm

1.2.2 中层模型的遗传算法解码过程 1）设定初始时间步，t=1.依据上层模型输入，初始化各节点的可用应急救援设施数量=xi,uRE,u和后勤保障资源数量=xi,uRM,u.初始化待恢复路段优先度V为受损路段的数目 |A*|.基于式（17）初始化各路段的运营状态.转到步骤2）.

2）基于Dijkstra 算法，生成t时间步路网状态下的所有后勤保障资源布设节点与所有受损路段间的最短路径以及所有应急救援设施所在节点与所有受损路段相邻节点间的最短路径，转到步骤3）.

3）判断优先级为V的受损路段a的状态，若=1，则无须为该路段分配应急救援设施和后勤保障资源，转到步骤10）；否则，转到步骤4）.

4）判断优先级为V的受损路段a相连节点是否有可达应急救援设施.若有，则计算可达应急救援设施数量，记为UE，转入步骤5）；否则，转入步骤10）.

5）判断优先级为V的受损路段a是否有可达后勤保障资源.若有，则计算可达后勤保障资源数量，记为UM，转入步骤6）；否则，转入步骤10）.

2 研究数据

为了验证上述模型和算法的有效性，基于贵州省2020 年7 月24 日高速公路门架数据，以毕节市、六盘水市、安顺市和贵阳市内部分区县组成的区域高速公路网为研究对象，构建无向拓扑网络.如图3 所示，以县（区）为网络节点，其中地级市管辖范围内的区被划为一个节点，如贵阳市的白云区、云岩区和观山湖区等均归为节点3.研究区域内有20 个节点、27 条路段、380 对OD.各路段的参数如表1 所示.各节点的加权客流介数ζn如图4 所示.图中，n为节点编号.加权客流介数为最短路经过该节点的OD 客流量之和与路网总客流的比值，用于表示各节点重要程度[21].假设重大自然灾害导致路网中15 条路段受到不同程度的损害，各受损路段的受损程度如表2 所示.通过穷举出15 条受损路段所有连通情况下的路网状态，获得恢复过程中不同路网状态下的未满足出行需求、用户出行阻抗增量以及后勤保障资源运输成本，计算得到最佳的目标函数加权因子cW、cZ和cM，分别为1 单位资金/veh、0.01 单位资金/(h·veh)和0.1 单位资金/h，以保证在路网恢复过程中PW始终大于PM和PZ，PZ始终大于PM.只考虑一种类型的应急工作站点，其中RE,u=20，RM,u=1 000，bu=0.模型中的其他参数取值如下：ρM=1 veh/h，ρE=30 (veh·h-1)/h，Δt=10 h.

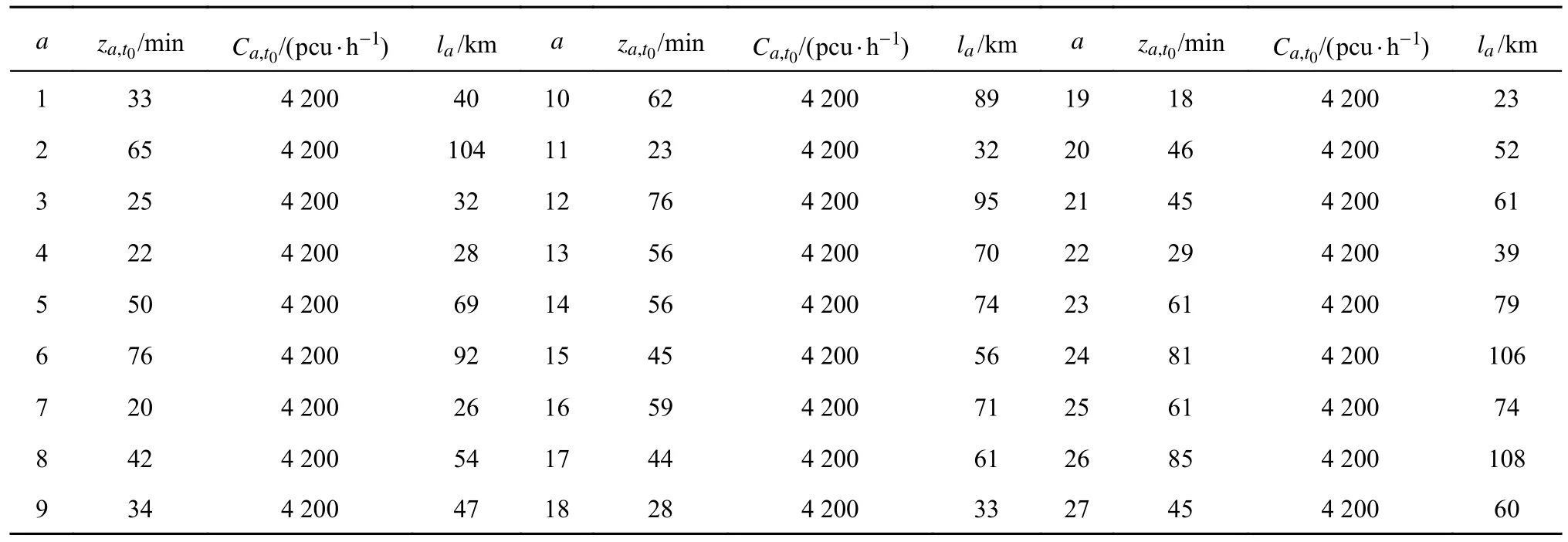
表1 贵州省区域高速公路网的路段参数Tab.1 Link parameters of Guizhou regional expressway network

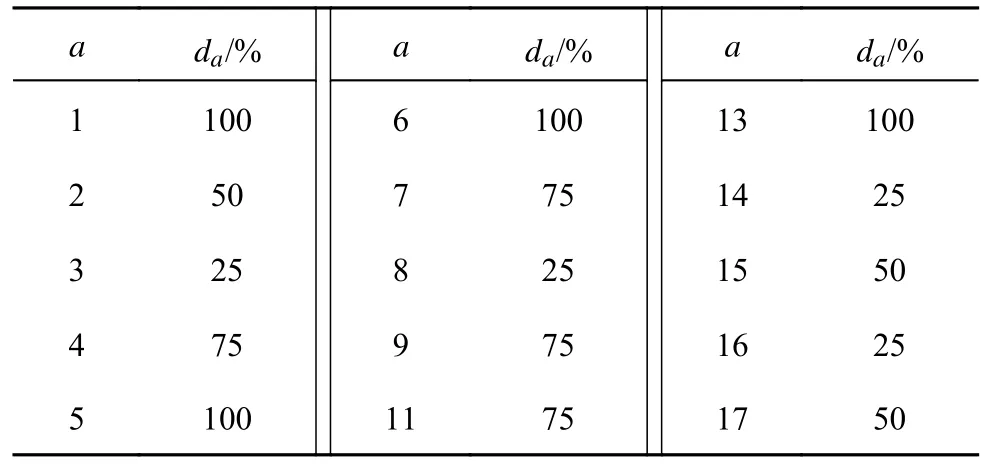
表2 受损路段的参数Tab.2 Parameters of damaged road section

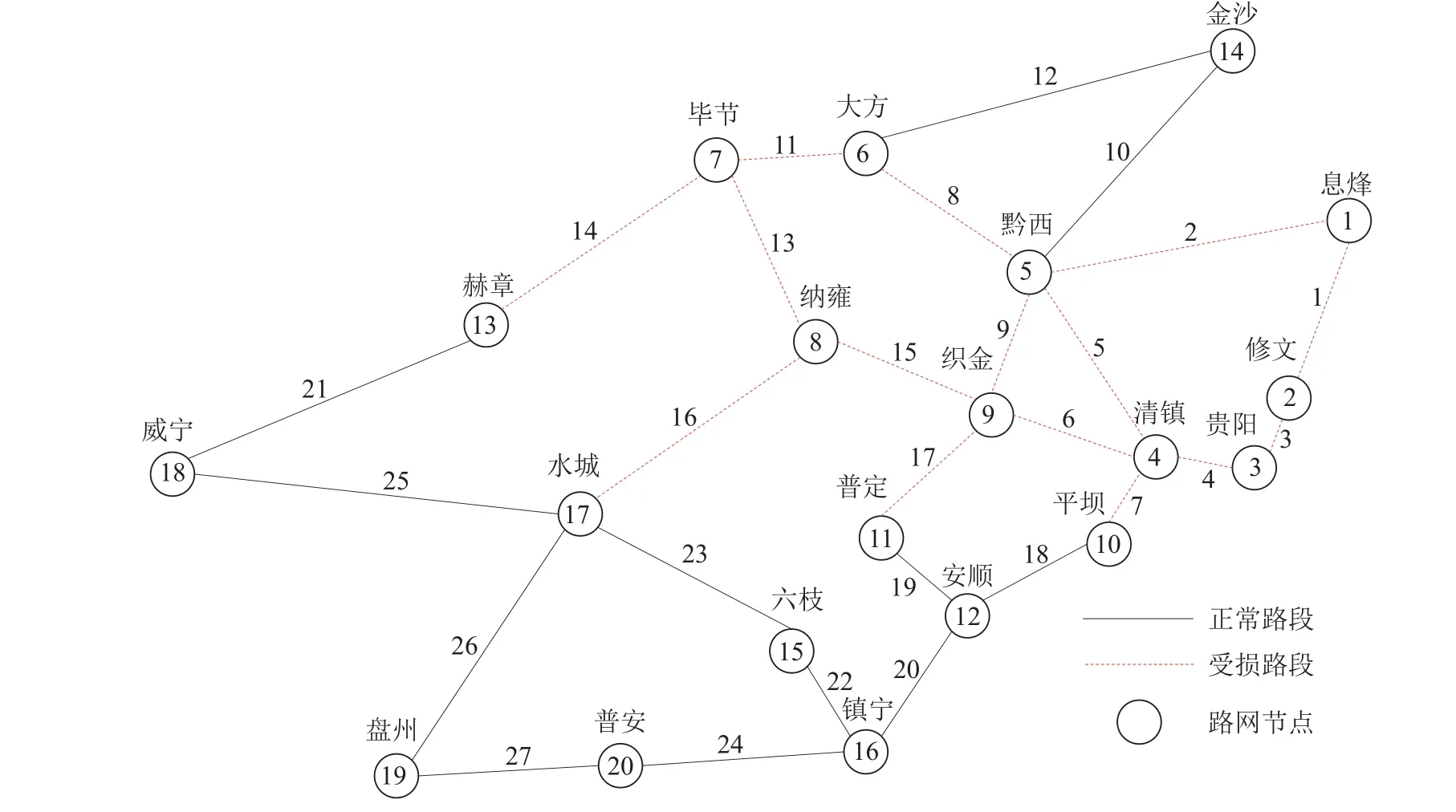
图3 贵州省区域高速公路网Fig.3 Guizhou province regional expressway network

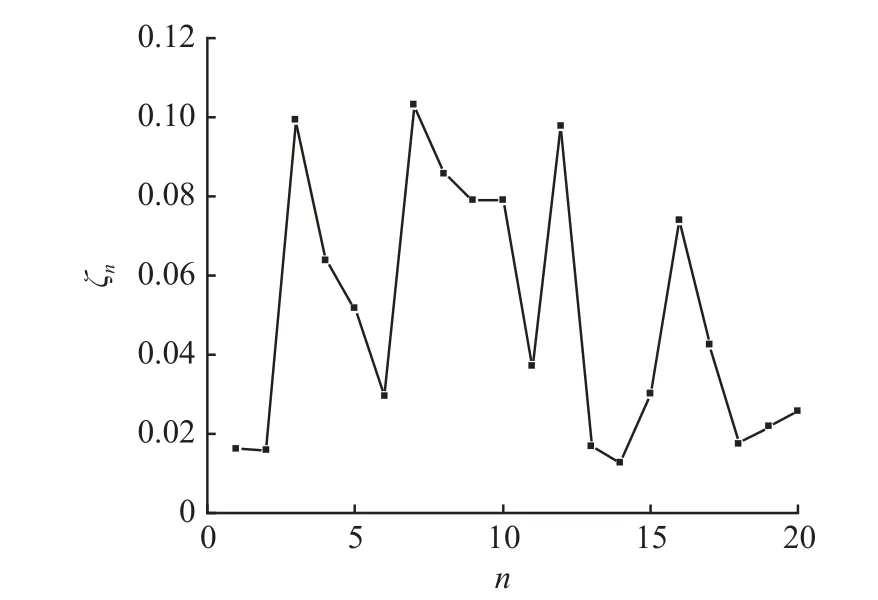
图4 路网各节点的客流介数Fig.4 Passenger betweennesses of each node of road network

3 案例分析

3.1 灾前工作站点布设决策的分析

为了验证路网多阶段抗灾决策优化中考虑后勤保障资源和路网恢复效果的必要性，对比分析包含提出的最优布设决策P、未考虑后勤保障资源的布设决策P1 和基于P-中值模型的布设决策P2[22].其中，在决策P1 下，所有受损路段都有充足的后勤保障资源，恢复过程的进行只受应急救援设施排程调度的影响.决策P2 在灾前恢复工作节点数目确定的情况下，保证各路段到工作站点的距离和最小，未考虑灾前布设对灾后恢复效果的影响.设定恢复工作站点布设数量B为1～5，变动幅度为1.如表3 所示为不同B下不同布设决策的结果.如图5 所示为不同B下不同布设决策的灾后路网恢复效果.

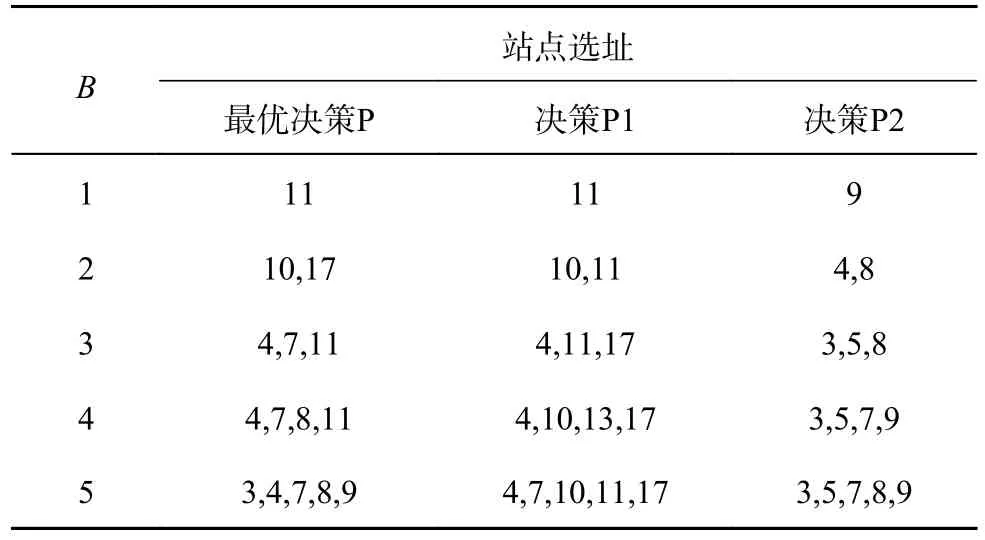
表3 不同预算下的灾前工作站点选址决策Tab.3 Pre-disaster work site deployment decisions under different budgets

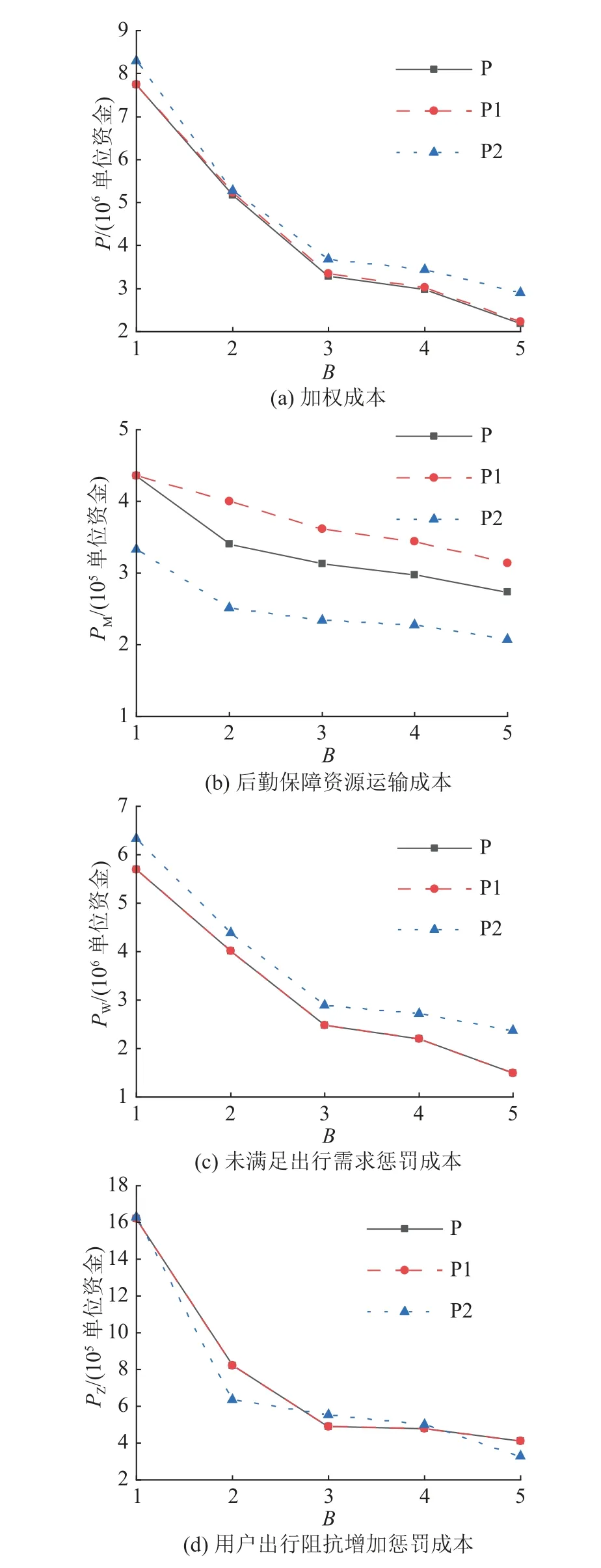
图5 不同预算下不同灾前布设方案的灾后路网恢复效果Fig.5 Post-disaster road network recovery effects of different predisaster deployment decisions under different budgets

如图5 所示，对比最优决策P 和决策P1 可知，两者对灾后路网恢复效果影响的差异主要体现在后勤保障资源运输成本.5 种预算下考虑后勤保障资源的灾前布设决策可以平均降低10.96%的PM，对PW和PZ没有影响.这是因为两布设决策的差异不影响灾后不同时间步应急工作站点到受损路段的可达性.如图6（a）所示，无论是最先恢复的路段14，还是后续恢复的路段7、4、13，还是再其次恢复的路段5、6、2 等，最优布设决策P 和布设决策P1 中的应急工作站点到这些路段均是可达的.两方案的差异未影响不同时间步最优决策对优先恢复路段的选择.两方案中应急工作站点抵达受损路段的路径长度有很大差异.如第1 个时间步，决策P 中站点17 抵达受损路段14 的最短路径为25-21，不同于决策P2 中节点11 的抵达路径19-20-22-23-25-21.第4 个时间步，站点17 抵达受损路段7 的最短路径为23-22-20-18，不同于站点11 的抵达路径19-18.灾前布设决策中是否考虑后勤保障资源对最优的灾后路网恢复时序没有影响，但会显著影响后勤保障资源的运输路径，进而影响后勤保障资源运输成本.

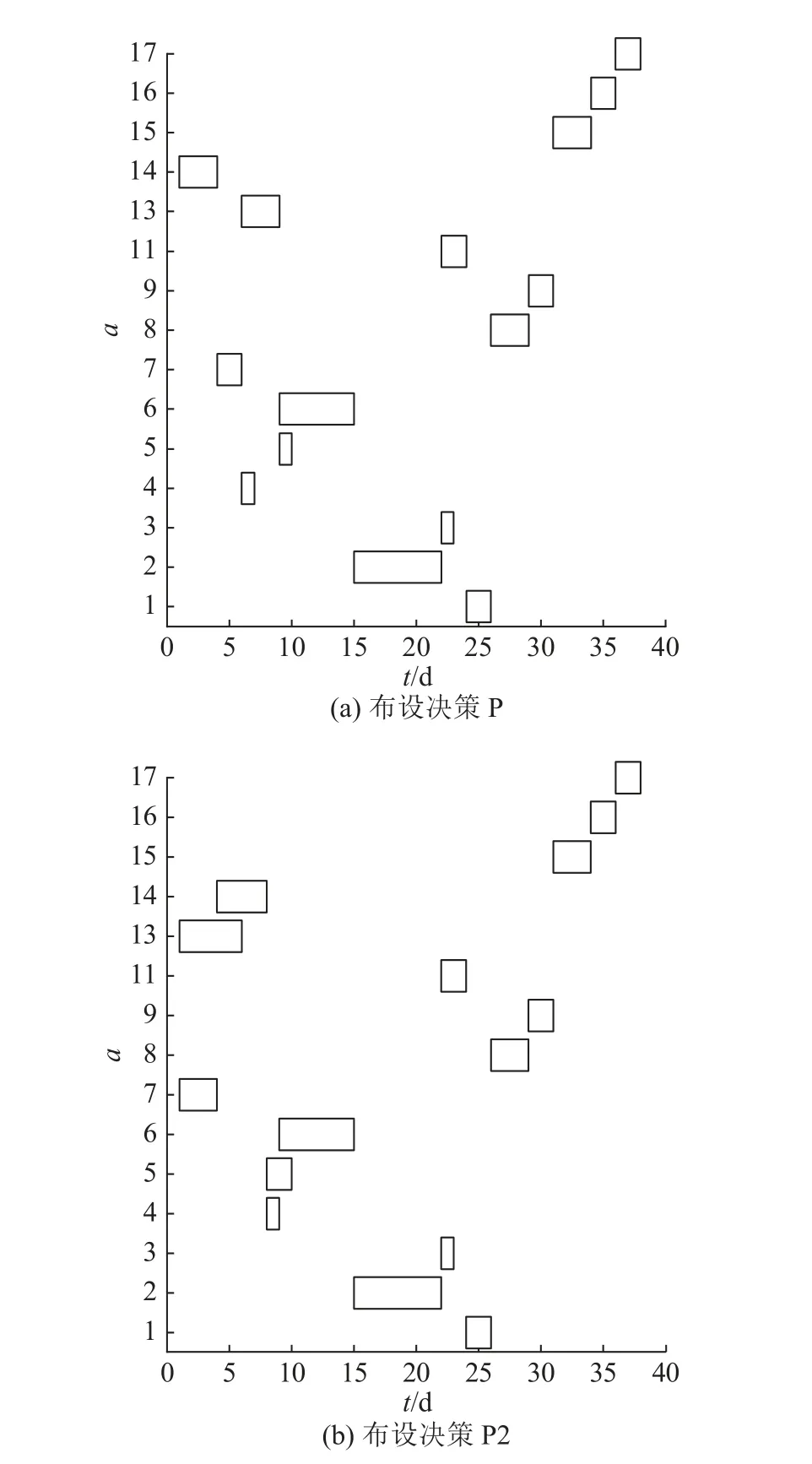
图6 B=2 下灾前布设决策P 和决策P2 对应的灾后路网恢复排程甘特图Fig.6 Post-disaster road network recovery effects of pre-disaster deployment decision P and decision P2 under budget B=2

如图5 所示，与决策P2 相比，5 种预算下最优决策P 分别平均降低了11.51%和17.73%的P和PW，平均增加了32.68%和7.88%的PM和PZ.这是由于2 种布设决策下的应急工作站点到受损路段的可达性不同，导致灾后受损路段的恢复时序不同.如图6（b）所示，由于决策P2 下的恢复工作站布设节点4、8 都无法抵达受损路段14，须先等待路段7、13 恢复完成，导致客流介数较大的节点3、7 在第7 个时间步非完全中断.在最优决策P 下，节点3、7 在第4 个时间步可以抵达路网中的大部分节点.网络中存在大量的受损路段，连通OD 的出行阻抗比灾前大，此时连通的OD 数量越多，用户出行阻抗增量越大，因此，最优决策P 下的未满足出行需求惩罚成本PW较小，用户出行阻抗增加惩罚成本PZ较大.基于P-中值模型的优化目标是最小化所有工作站点到受损路段的距离和，因此后勤保障资源的运输成本更小.上述结果表明，考虑灾后路网恢复效果的灾前布设决策能够有效地保障网络中关键节点的快速连通.

3.2 灾后受损路段恢复决策的分析

为了分析后勤保障资源与应急救援设施的相互协作关系对灾后路网恢复效果的影响，对比分析B=2 下不同RE,u和RM,u的最优路网恢复决策及不同RE,u的未考虑后勤保障资源的恢复决策的恢复效果.

如图7 所示，设定每个工作站点的RM,u为固定值1 500，RE,u为1～5，变动幅度为1.如图8 所示，设定每个工作站点RE,u为固定值4，RM,u为500～3 000，变动幅度为500.随着RE,u或RM,u的增加，P、PW和PZ都先呈现减小趋势，后保持不变.三者随RE,u增加的平均降低速度分别为15.00%、16.17%和16.64%，平均降低幅度为1.55×106、1.14×106和0.47×106单位资金.三者随RM,u增加的平均降低速度分别为9.34%、7.83%和7.59%，平均降低幅度为1.55×106、1.14×106和0.47×106单位资金.这是因为保持RM,u或RE,u中的某一项为固定值，增加另外一项，均会使单位时间步能够恢复的路网受损容量变大，路网能够更快地恢复到灾前状态，因此PW和PZ都会减小.PW和PZ所占的权重更大，因此P呈减小的趋势.当RE,u由4 增加到5 后，应急救援设施在单位时间步内需要的后勤保障资源超过了1 500.此后增加RE,u将无法修复更多的路段，各类恢复成本保持不变.当RM,u由1 500 增加到2 000 后，后勤保障资源在单位时间步内需要的应急救援设施超过了4，单独增加RM,u将无法恢复更多的路段.上述结果表明，后勤保障资源与应急救援设施的布设数量共同决定了灾后路网的恢复过程，仅增加其中一项都可能会造成资源浪费，只有两者相互协调才能得到最优的恢复效果.如图9所示，由于未考虑后勤保障资源与应急救援设施间的相互协作关系，PW和PZ始终随RE,u的增加而降低.其中，PW和PZ的平均降低速度分别为20.22%和20.54%，平均降低幅度为1.27×106单位资金和0.52×106单位资金，均高于最优决策.忽略后勤保障资源与应急救援设施间的依赖关系，将会高估应急救援设施布设数量的增加对路网恢复效果的影响.

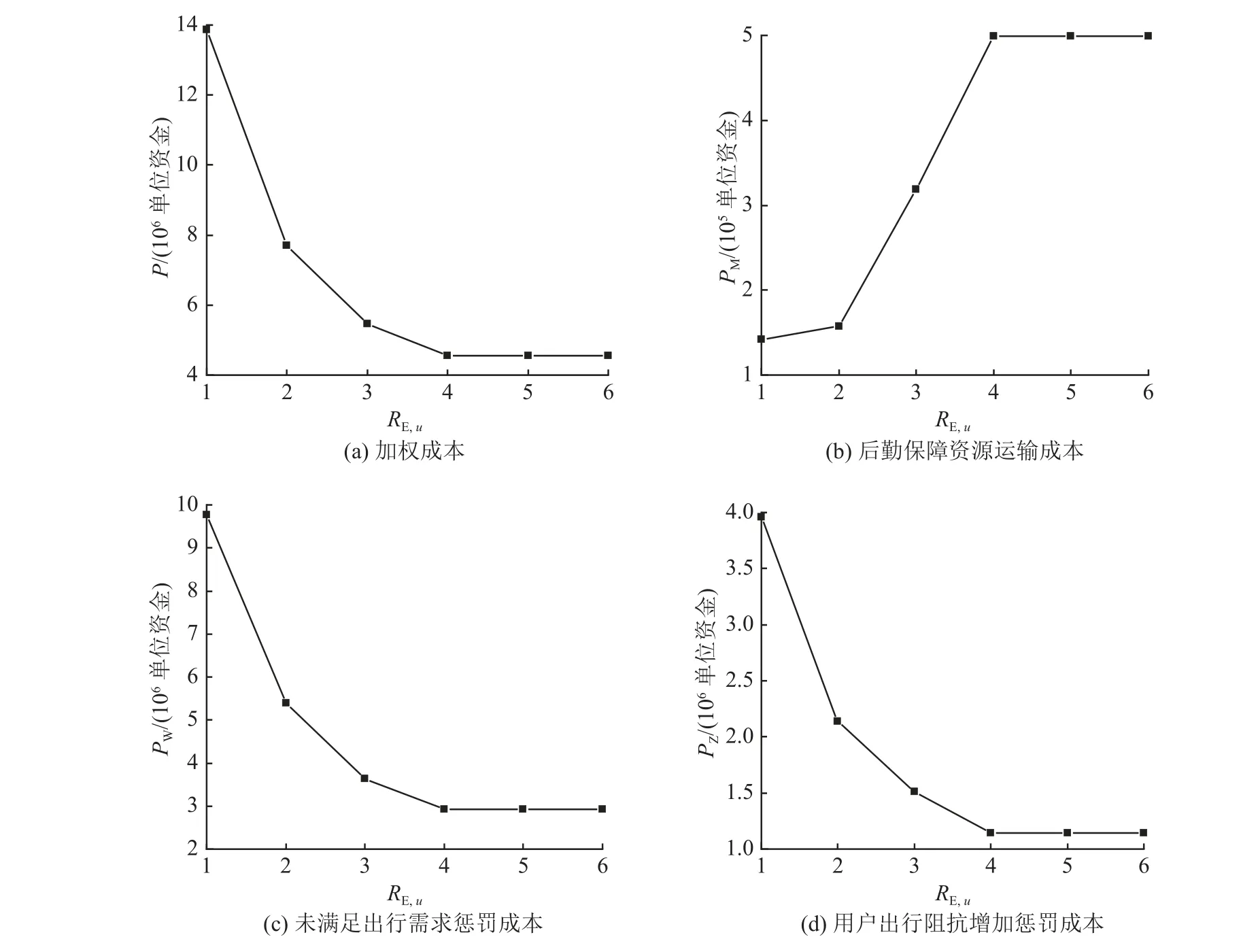
图7 B=2 下不同 RE,u 最优恢复决策的灾后路网恢复效果Fig.7 Post-disaster road network recovery effect of optimal recovery decision under different RE,u with B=2

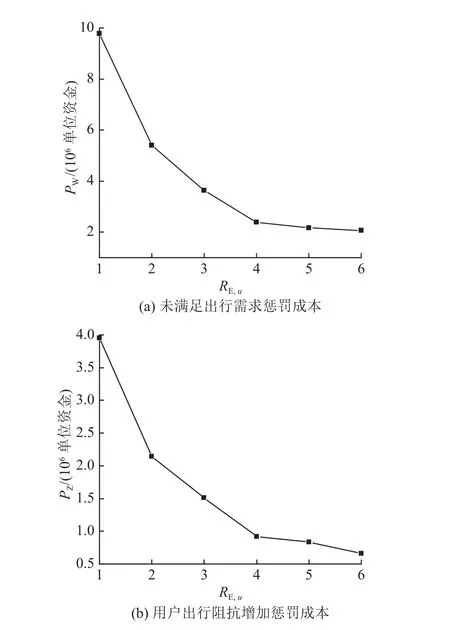
图9 B=2 下不同 RE,u 的未考虑后勤保障资源的恢复决策灾后路网恢复效果Fig.9 Post-disaster road network recovery effects of recovery decisions without considering logistical support resources for different RE,u under B=2

对比图7（b）、8（b）可知，保持RM,u或RE,u中的某一项为固定值，增加另外一项，PM的变化是相反的.如图7（b）所示，随着RE,u的增加，PM呈现出增大的趋势，平均增大速度为34.04%，平均增大幅度为7.15×104单位资金.这是因为当RE,u较小时，单位时间步可以恢复的受损路段数量有限，大量后勤保障资源可以在恢复后期路网连通性恢复到一定程度后，通过较短路径运往受损路段.随着RE,u的增加，单位时间步能够恢复的路段数量会增加.由于在恢复早期路网中存在大量的不连通路段，应急工作站点抵达受损路段的路径成本和PM更大.如图8（b）所示，随着RM,u的增加，PM呈现出减小的趋势，其中平均减小速度为36.40%，平均减小幅度为1.17×105单位资金.这是因为当RM,u较小时，距受损路段最近的工作站点无法提供足量的后勤保障资源，须从其他距离较远的工作站点调配资源.随着RM,u的增加，距受损路段较近的工作站点能够提供的后勤保障资源越多，因此后勤保障资源运输成本越低.当RM,u增加到2 500 单位资金后，距受损路段较近的工作站点能够提供该路段恢复所需的全部后勤保障资源，PM将不再随RM,u的增加而变化.

4 结论

（1）利用构建的路网抗灾能力决策优化模型，可以有效地降低路网灾害应对成本.较未考虑后勤保障资源的灾前布设决策，该模型通过优化后勤保障资源的运输路径，有效降低了后勤保障资源的运输成本.与未考虑灾后恢复过程的灾前布设决策相比，该模型能够保证网络中关键节点的快速连通，有效降低了未满足出行需求的惩罚成本.

（2）后勤保障资源和应急救援设施共同决定灾后路网恢复过程.当其中一项所能恢复的路段容量超过另一项时，增加其数量将无法改善路网的恢复效果.忽略两者间的协作关系，将会高估应急救援设施布设数量的增加对恢复效果的影响.在路网恢复过程中，需要确保后勤保障资源和应急救援设施数量的相互匹配，以提高路网恢复效率，避免资源浪费.

（3）后勤保障资源和应急救援设施数量的变化会对后勤保障资源运输成本产生相反的影响，随着应急救援设施数量的增大而增大，随着后勤保障资源数量的增大而减小.在实际应用中，需要准确认识和辨析后勤保障资源和应急救援设施数量变化对路网恢复效果的影响.

（4）为了降低模型求解的复杂度，仅考虑一种类型的应急工作站点.考虑到不同路段的受损程度、初始容量、恢复优先程度等不同，它们对在其周围布设的应急救援设施和后勤保障资源的需求有差异.下一步将研究考虑多种类型灾前应急工作站点的道路交通网络多阶段抗灾能力优化问题.