基于磁热耦合法的非对称混合磁极永磁电机热分析

史立伟，刘政委，乔志伟，赵新，朱英杰

(山东理工大学 交通与车辆工程学院，山东 淄博 255000)

永磁电机因其结构简单无励磁绕组并使用永磁体提供磁通，相较于其他电机，永磁电机具有高转矩密度、高功率密度及运行可靠等方面的优势，被广泛应用于新能源汽车、航空航天、船舶、车床等领域[1-3].永磁电机存在一些不足之处：电枢绕组均位于定子槽中，热源相对集中，在发热量增大的同时会造成电机散热困难，永磁电机的温升直接影响电机的运行性能和可靠性；电机温度过高会造成电磁材料性能降低，加剧永磁体不可逆高温退磁的风险.准确分析永磁电机的温升分布以减少发热量，对提高电机的可靠性及保证电机性能的稳固性至关重要.

常用的电机热分析方法可以分为等效热网络分析法和数值方法2 种，数值方法可以细分为有限元法和计算流体动力学方法[4-6].等效热网络方法的计算速度快，但需要大量实验和经验公式来构建传热路径，无法得到电机温度分布及最高温度，因此等效热网络法多用于简单温升预测.利用有限元法和计算流体动力学方法均能够准确预测温升分布，但计算流体动力学方法对模型设置的要求非常高，且计算机要求高，难以做到广泛应用.

国内学者针对电机温升分析取得了丰硕的成果.针对不同电机进行热分析时所关注的重点有所不同.针对开关磁阻电机的热分析多集中于绕组方面，Zhang 等[7-9]提出绕组分层建模，提高等效热网络法的精度，采用有限元法对电机进行热分析.史立伟等[10]提出短磁路分块定子结构，降低电机铁损，提升效率.对永磁电机进行热分析时，永磁体是重点.韩雪岩等[11-12]采用三维温度场模型，对电机进行热分析；Shi 等[13]构建永磁同步直线电机的三维集总参数热网络模型，对电机进行热分析.丁树业等[14]采用等效热网络法，分析电机启动和稳态下温升的分布情况；吴胜男等[15-17]采用集中参数热网络法和数值方法结合的方法，对永磁电机进行热分析；目前针对永磁电机热分析的研究大部分仅限于热场分析，对于如何降低电机温度的研究较少，且较少有文献采用磁热耦合方法对永磁电机进行热分析，特别针对混合磁极永磁电机采用磁热双向耦合方法考虑温度对材料影响的热分析更少.

本文介绍非对称混合磁极永磁电机（asymmetric hybrid pole permanent magnet motor）和传统内置式永磁电机的结构特点，分析非对称混合磁极永磁电机的电磁特性和损耗产生机理，对比分析2 种电机的损耗,阐明非对称混合磁极永磁电机低损耗的原因.搭建电机集中参数热网络模型，针对电枢绕组的结构特点及其在定子槽中的布置方式对其进行等效，确定电枢绕组的等效导热系数.建立三维单向和双向磁热耦合有限元模型，将电机的不同损耗精确传递到电机各部分进行热分析，对比不同分析方法、不同电流密度的电机温升.试制一台样机,搭建实验平台进行测试.本文的研究工作为提高相似冷却条件和功率等级下的永磁电机的温升分析精度提供了一种可供参考的方法.

1 电机结构及特性分析

1.1 电机结构

以非对称混合磁极永磁电机为研究对象.电机的额定功率为5 kW，额定电压为72 V，额定转速为3 000 r/min.非对称混合磁极永磁电机采用8 极48 槽结构，电枢绕组为分布式绕组.为了对比分析非对称混合磁极结构对电机性能带来的影响，将传统内置式永磁电机作为对比基准，2 种电机转子的结构如图1 所示.图中，黑色箭头为永磁体充磁方向.传统内置式永磁电机励磁源均为永磁体，永磁体采用V 型排布方式且每块永磁体的尺寸均一致.非对称混合磁极永磁电机采用永磁体与铁氧体共同励磁.钕铁硼1、钕铁硼2、钕铁硼3、钕铁硼4 的体积各不相同，钕铁硼1 的宽度为10.8 mm，钕铁硼2 的宽度为7.9 mm，钕铁硼3 的宽度为14.8 mm，钕铁硼4 的宽度为11.9 mm.

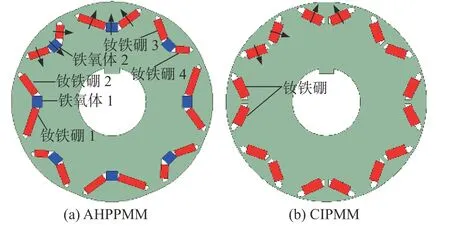
图1 非对称混合磁极永磁电机及传统内置式永磁电机的转子拓扑结构Fig.1 Rotor topology of asymmetric hybrid pole permanent magnet motor and conventional interior permanent magnet motor

2 种拓扑结构的简化磁路如图2 所示.图中，z直线为主磁通路径，曲线路径为漏磁通路径.从图2 可以看出，V 型结构相邻磁极间的磁通路径均为从一侧永磁体出发经转子铁芯、气隙、定子齿、定子轭部、定子齿、气隙、转子铁芯、另一侧永磁体、转子铁芯，最后回到永磁体形成闭合回路.与传统内置式永磁电机的V 型结构相比，该非对称混合磁极结构在V 型结构磁路的基础上增加了并联磁路.该并联磁路为从铁氧体出发经转子铁芯、气隙、定子齿、定子轭部、定子齿、气隙、转子铁芯、另一侧永磁体、转子铁芯，最后回到铁氧体形成闭合回路.由于该并联磁路的增加使得非对称混合磁极永磁电机的总磁路磁阻降低，提升了总磁路中的有效磁通量，提高了电机磁场的利用率，同时能够保证在不降低电机输出转矩的同时减少永磁体用量.

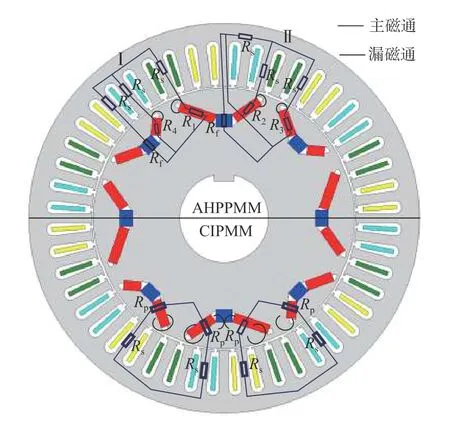
图2 非对称混合磁极永磁电机及传统内置式永磁电机的简化磁路对比图Fig.2 Simplified magnetic circuit comparison diagram of asymmetric hybrid pole permanent magnet motor and conventional interior permanent magnet motor

相较于传统内置式永磁电机每对V 型磁极夹角均一致，非对称混合磁极永磁电机钕铁硼1、钕铁硼2、钕铁硼3、钕铁硼4 与磁极中心线间的夹角为非对称夹角，钕铁硼1 与钕铁硼2 之间的夹角为119°，钕铁硼3 与钕铁硼4 之间的夹角为121.1°.非对称夹角不仅能够实现对气隙磁密波形的优化，降低气隙磁密波形的畸变率，还能够有效地降低电机的齿槽转矩.如图3 所示，非对称混合磁极永磁电机转子采用非均匀气隙结构.电机转子外缘由多段与定子内圆不同心的圆弧组成，转子偏心距h=7 mm，电机最小气隙长度 εmin=0.7 mm，最大气隙长度 εmax=1.31 mm.采用非均匀气隙结构，能够在降低空载反电势波形畸变率的同时减小电机转矩脉动，提升电机的输出性能.非对称混合磁极永磁电机与传统内置式永磁电机的主要参数对比如表1 所示.

表1 电机的主要几何参数Tab.1 Main geometric parameters of motors

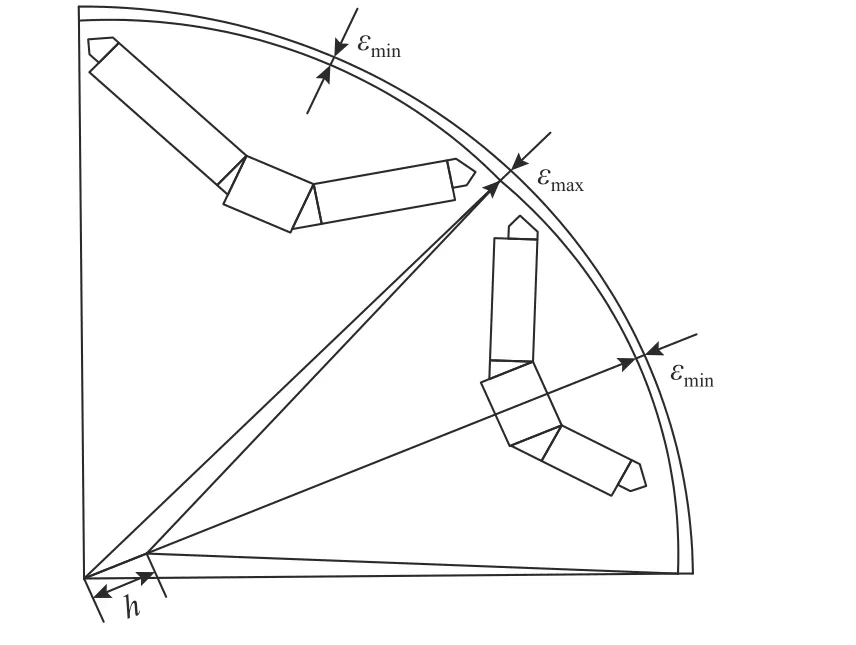
图3 非均匀气隙转子的结构Fig.3 Structure of non-uniform air gap rotor

1.2 电机的电磁特性分析

非对称混合磁极永磁电机与传统内置式永磁电机的磁场分布如图4 所示.可以看出，二者的隔磁桥处均出现磁通饱和现象，传统内置式永磁电机的每个V 型磁极中间出现了磁通饱和现象，而非对称混合磁极永磁电机因为在两钕铁硼间插入了铁氧体，避免了这一现象.电机定子齿均未出现磁通饱和的现象，这说明了电机结构设计的合理性.可以看出，与传统内置式永磁电机相比，非对称混合磁极永磁电机的磁通密度幅值提高，有效磁通量增大.

气隙磁通密度的对比如图5 所示.图中，θ 为转子角度.从图5 可以看出，与传统内置式永磁电机相比，非对称混合磁极永磁电机的气隙磁通密度幅值提高了12.85%.在额定转速3 000 r/min 下得到的非对称混合磁极永磁电机与传统内置V 型永磁电机反电势波形对比如图6 所示.图中，U为反电势.从图6 可以看出，非对称混合磁极永磁电机的空载反电势幅值由31.15 V 提升至38.01 V.

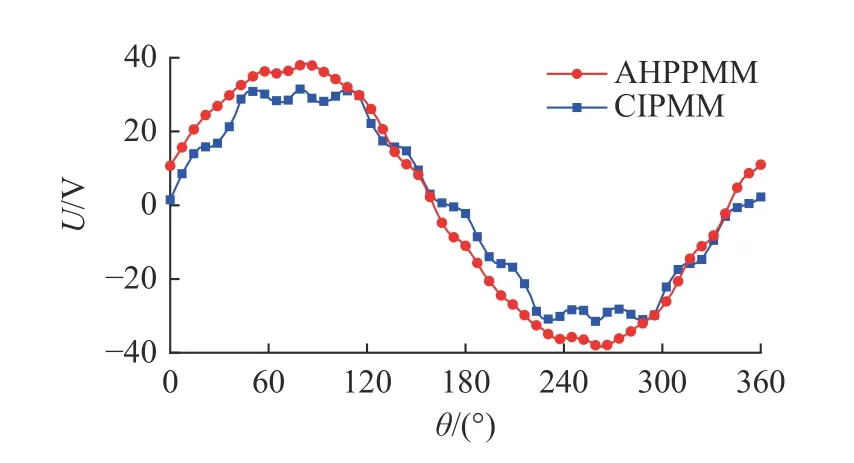
图6 空载反电势的波形Fig.6 Waveform of no-load back EMF

THD(total harmonic distortion)即总谐波失真，用于量化信号中的谐波成分对原始信号的扭曲程度.THD 的表达式为

气隙磁通密度的谐波分析对比如图7 所示，非对称混合磁极永磁电机的基波幅值提高，大部分高次谐波幅值均降低.图中，Bmn为气隙磁通密度的谐波幅值.从式(1)可知，气隙磁通密度THD降低，气隙磁通密度的波形失真程度下降，正弦化程度提高.空载反电势波形的谐波分析对比如图8 所示.可知，非对称混合磁极永磁电机的反电势基波幅值增大.计算式(1)可知，THD 由传统内置式永磁电机的9.97%降低为非对称混合磁极永磁电机的4.35%.

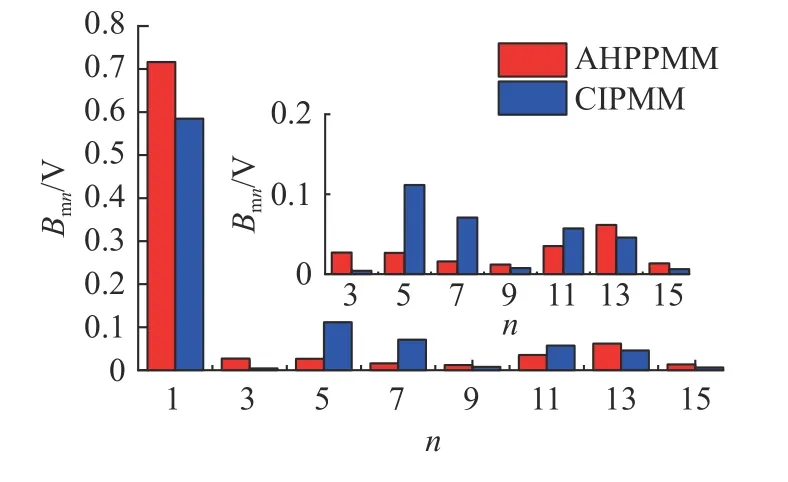
图7 气隙磁通密度的谐波分析Fig.7 Harmonic analysis of air gap flux density

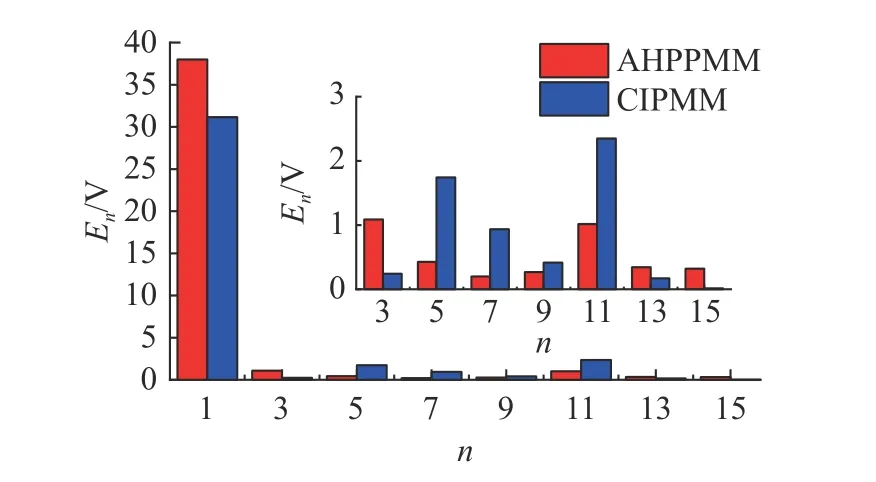
图8 空载反电势的谐波分析Fig.8 Harmonic analysis of no-load back EMF waveform

1.3 电机损耗分析

永磁电机的损耗主要分为以下3 类: 铁芯损耗、绕组铜损和永磁体涡流损耗.铁芯损耗包括磁滞损耗、涡流损耗和附加损耗，铁芯损耗可以利用Bertotti 计算模型[18]得到：

式中：kh为磁滞损耗系数，ke为涡流损耗系数，kc为附加损耗系数，B为磁通密度幅值，f为气隙磁场频率.

电机的铜损为电枢绕组通电以后每个线圈上的铜耗之和，表达式为

式中：m为相数，I为相电流的有效值，R为每相绕组的电阻.

永磁体涡流损耗的产生存在不同机理.理想气隙磁通密度波形为正弦波形，定子开槽会导致该处气隙磁通密度凹陷，导致气隙磁通密度中的高次谐波含量增大，高次谐波使得永磁体表面产生涡流损耗.转子采用非均匀气隙结构，能够对气隙磁通密度进行正弦化调制，降低气隙磁通密度中的高次谐波含量.电机转子永磁体涡流损耗的简化计算公式可以表示为

式中：V为永磁体的体积，b为永磁体的平均宽度，h为永磁体的轴向长度，ρ 为永磁体的电阻率，fn为永磁体中磁通密度的变化频率.由式（4）可知，永磁体涡流损耗受永磁体体积的影响，涡流损耗与永磁体体积正相关；因此，减小永磁体体积，可以减少永磁体的涡流损耗.将内置V 型永磁体一侧永磁体分段，采用电导率高的铁氧体代替部分永磁体，能够保证电机输出相同转矩的情况下，减少永磁体的用量和电机的涡流损耗.

将电机转速设定为额定工作转速3 000 r/min，对比2 种电机的损耗.图9 中，t'为时间.从图9 可知，在额定工况下，传统内置永磁电机的涡流损耗平均值为36.12 W，非对称混合磁极永磁电机的涡流损耗平均值为25.55 W，涡流损耗降低了29.26%.如图10 所示，传统内置永磁电机的铁芯损耗平均值为158.63 W，非对称混合磁极永磁电机的铁芯损耗平均值为129.42 W，铁芯损耗降低了18.41%.在保证输出功率为5 kW 的条件下，电机的总损耗PT随着转速nr的变化情况如图11 所示.可知，随着转速的提升，电机总损耗增加，铁芯内部磁场的交变频率提高，由式(1)可知，电机的铁芯损耗随之提升.在全转速范围内，传统内置式永磁电机的总损耗均高于非对称混合磁极永磁电机.在额定转速为3 000 r/min 的条件下，与传统内置式永磁电机相比，非对称混合磁极永磁电机的总损耗下降了21.79%.

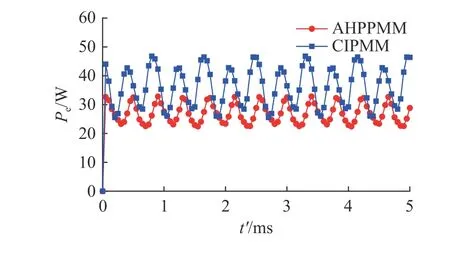
图9 涡流损耗的对比Fig.9 Comparison of eddy current loss

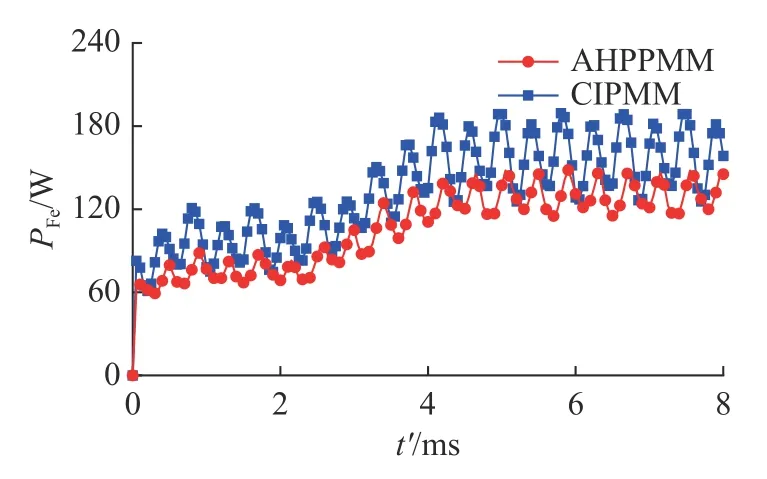
图10 铁芯损耗的对比Fig.10 Comparison of iron core loss

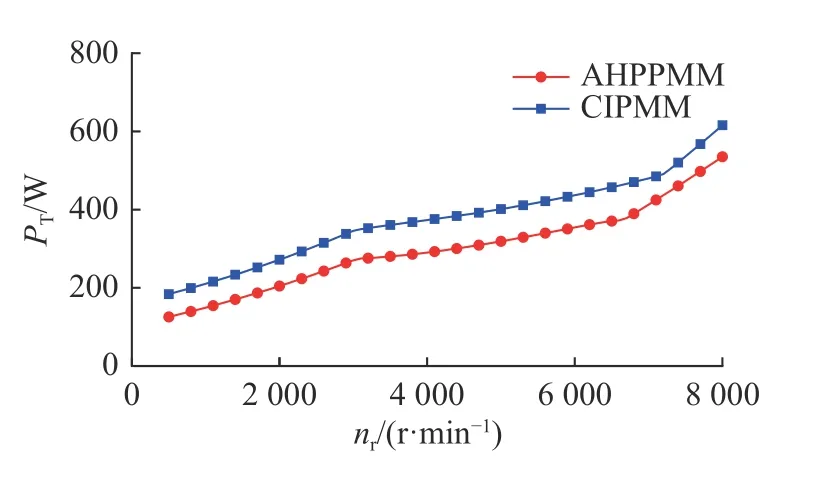
图11 总损耗的对比Fig.11 Comparison of total losses

2 集中参数热模型的建立

2.1 集中参数热模型

对电机采用集中参数模型进行热计算，为了便于建立集中参数热模型以方便求解，在建立模型前给出以下假设.

1）忽略电机定子槽内绕组的集肤效应.

2）电机内各热源分布均匀，电机杂散损耗集中于定子齿部.

3）电机内部的热量仅通过热传导和热对流进行交换，忽略热辐射部分的影响.

基于上述假设，结合非对称混合磁极永磁电机的结构特点及传热特性，通过集中参数热网络法将电机各部分的温度场划分为若干个区域.将区域中心作为节点，不存在损耗的节点为无源节点，存在损耗的节点为有源节点，各节点之间通过热阻相互连接，形成正交网络拓扑结构.在提出的模型中，考虑热传导和热对流这2 种传热方式.该集中参数热网络模型包含30 个节点，其中定子壳5 个节点，节点之间的热阻包括传导热阻、对流热阻.定子轭部3 个节点之间的热阻仅包括传导热阻.电枢绕组5 个节点中，两端节点存在对流热阻、传导热阻，中间节点仅存在传导热阻.定子齿部3 个节点间存在传导热阻、对流热阻.转子极靴3 个节点存在传导热阻、对流热阻.永磁体4 个节点间仅存在传导热阻.转子轭部3 个节点间仅存在传导热阻.轴承和端盖各有2 个节点，节点间仅存在对流热阻.建立永磁电机的集中参数热模型，如图12 所示.

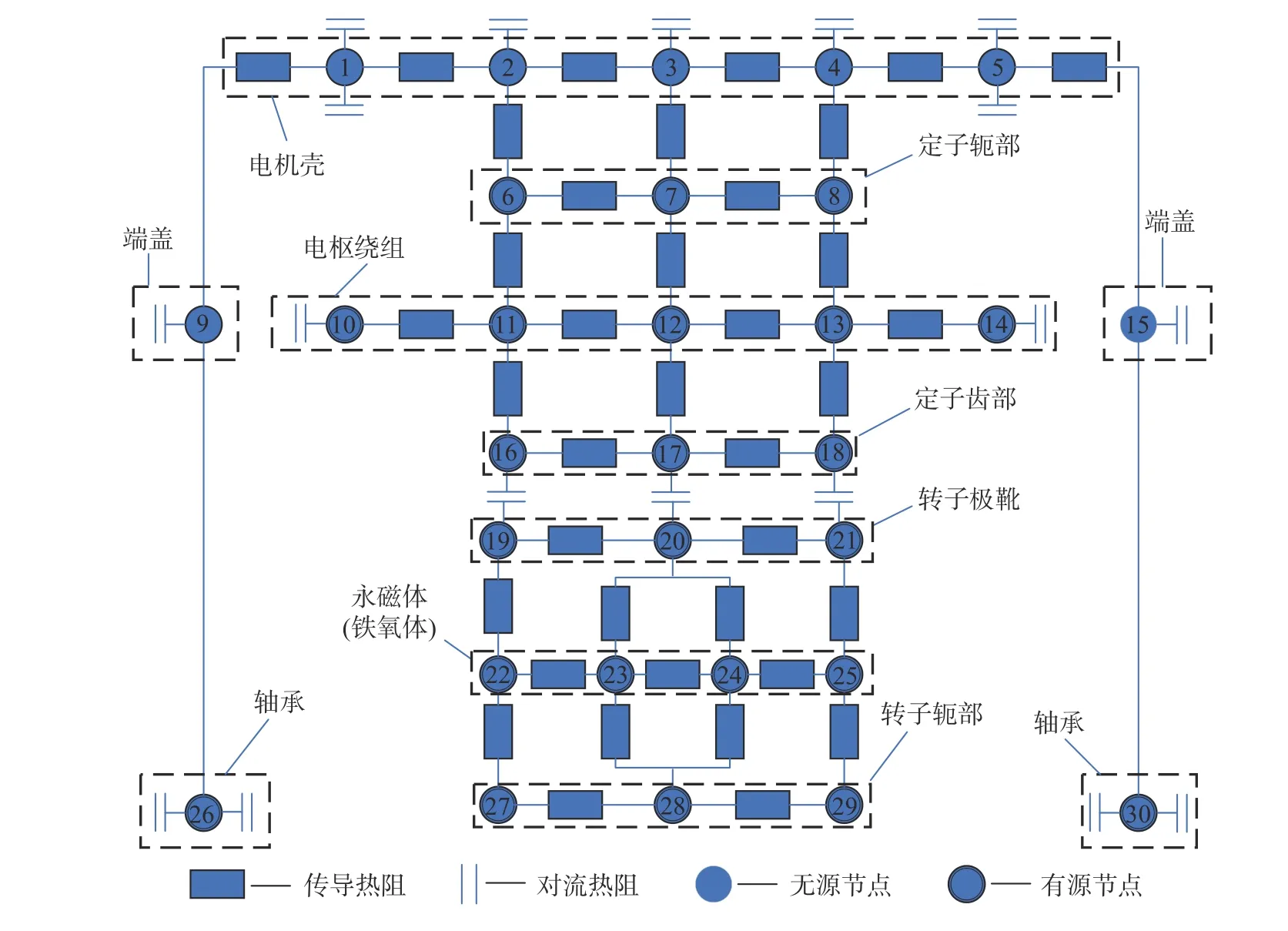
图12 非对称混合磁极永磁电机的集中参数热网络模型Fig.12 Lumped parameter thermal network of asymmetric hybrid pole permanent magnet motor

传导热阻是指当热量以热传导的方式通过某一物体时，热量在物体内所遇到的阻力.传导热阻定义为

式中：L为沿传导热量方向的长度，λ 为材料的导热系数，Sd为导热面积.

对流热阻是固体零件表面与流体之间的热阻，表达式为

式中：α 为对流散热系数，Sα为对流散热面积.非对称混合磁极永磁电机的导热系数λ、比热容c、密度ρ 如表2 所示.

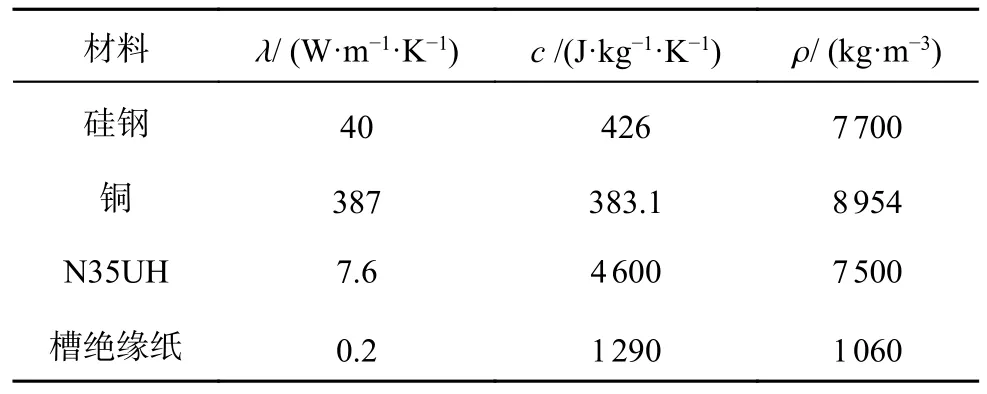
表2 非对称混合磁极永磁电机的材料参数Tab.2 Material data of asymmetric hybrid pole permanent magnet motor

2.2 等效电枢绕组

在实际电机定子槽内的填充材料为多种材料，由铜导线、绝缘漆、绝缘纸组成.定子槽内的绕组之间存在空气间隙，因此定子槽内的部分热量在进行传递时，热量传递方向不能准确求得.在建立等效网络模型时，需要将定子槽内绕组及各种绝缘材料等效为径向和轴向导热系数不同的整体.电机定子齿和电枢绕组如图13(a)所示，铜线表面覆盖绝缘漆构成漆包线，漆包线缠绕在定子齿上构成电枢绕组，电枢绕组与定子齿之间采用绝缘纸隔绝.同一定子槽中包含双层绕组，左、右层电枢绕组间存在空气间隙，由于空气的导热系数极小，左、右两层电枢绕组间几乎没有热量传递，电枢绕组产生的热量绝大部分通过定子齿传导散热.

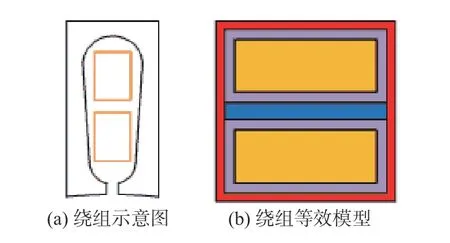
图13 非对称混合磁极永磁电机绕组的示意图及等效模型Fig.13 Schematic diagram and equivalent model of winding for asymmetric hybrid pole permanent magnet motor

等效后的电枢绕组如图13(b)所示.铜线、绝缘漆和绝缘纸不同传热方向的厚度不同，根据槽宽、槽深进行折算.定子槽中电枢绕组沿轴向的等效热系数为

式中：lxi分别为铜线、绝缘漆、绝缘纸沿x方向的厚度，λi为铜线、绝缘漆、绝缘纸3 种材料的导热系数.定子槽中电枢绕组沿径向的等效导热系数为

式中：lyi分别为铜线、绝缘漆、绝缘纸沿y方向的厚度.定子铁芯与电枢绕组之间的等效传导热阻为

式中：L为定子槽中电枢绕组沿热流传导方向的长度，λe为定子槽中电枢绕组的等效导热系数，S为定子铁芯和电枢绕组之间的接触面积.

2.3 计算结果

根据热平衡原理可知，在稳态情况下电机每个单元产生的热量及传入的热量应等于从单元输出的热量.分别构建热导矩阵G、节点温度矩阵T、热源矩阵W，列出等效热平衡方程：

根据以上确定的电机散热条件和电机各部分损耗分布，利用建立的集中参数热网络模型，对永磁电机的温升进行计算.各个部件的温升求解结果如表3 所示.

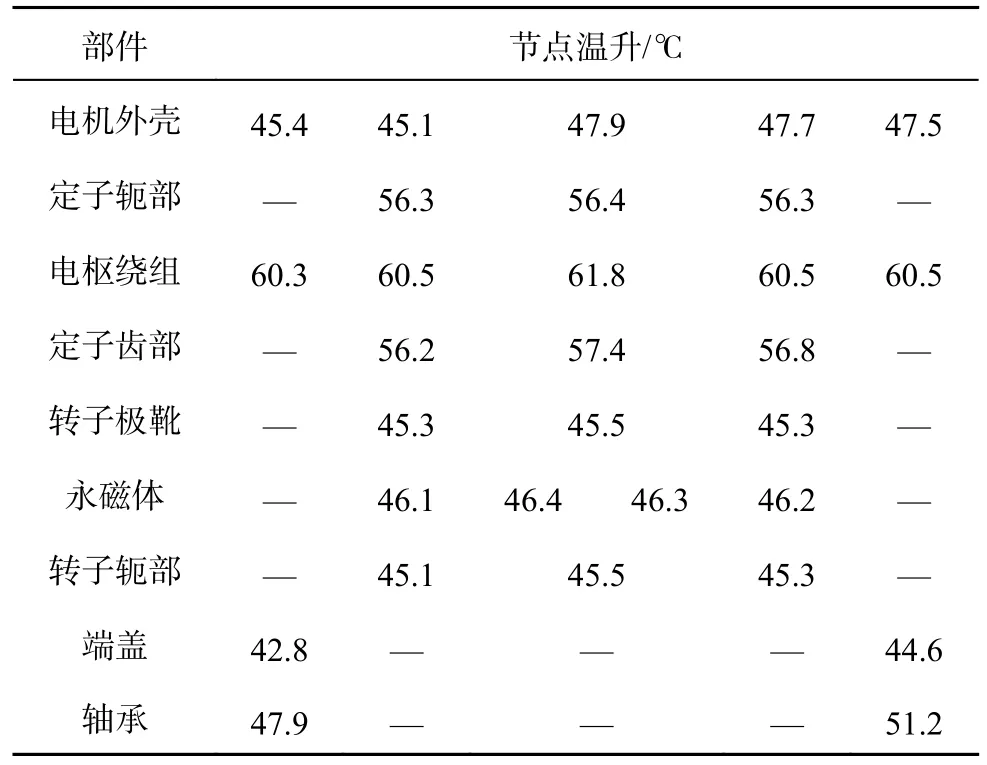
表3 非对称混合磁极永磁电机额定运行状态下的各部件温升计算结果Tab.3 Calculation results of temperature rise for each component under rated operation of asymmetric hybrid pole permanent magnet motor

从计算结果可以看出，电枢绕组端部温升低于定子槽内绕组温升，电机最高温升位于定子槽内的电枢绕组处，最高温升为61.8 ℃，电枢绕组的平均温升为60.7 ℃.定子轭部的平均温升为56.3 ℃，定子齿部的平均温升为56.8 ℃.电机转子的最高温升为45.5 ℃，永磁体的最高温升为46.4 ℃，永磁体的平均温升为46.3 ℃.

3 磁热耦合分析

3.1 单向磁热耦合分析

利用集中参数网络对电机进行热分析，能够简化模型，快速求解.集中参数热网络法存在弊端，虽然计算速度快，但无法直接得到电机各部件的温度分布.若部件较复杂，则集中参数热网络法求解困难且精度不高.为了能够进一步对电机进行热分析，验证集中参数热网络结果，对电机进行磁热耦合仿真.非对称混合磁极永磁电机存在对称电磁特性，但热学条件不对称.为了提高计算效率，电机的电磁特性分析采用二维场，对电机进行热力学仿真时采用三维场，三维图如图14 所示.

图14 非对称混合磁极永磁电机的三维图Fig.14 Three-dimensional diagram of asymmetric hybrid pole permanent magnet motor

在单向磁热耦合中，对电机在二维场中进行电磁特性分析.其中电机的定子铁芯损耗、转子铁芯损耗及永磁体的涡流损耗可以直接计算得到，通过电磁场计算得到的铁芯损耗、涡流损耗直接传递到三维热场中作为热源，为电机热分析做准备.绕组铜损需要在二维场中计算后，经过添加端部和槽内绕组交流铜耗系数分别修正绕组各部分铜耗后，再传递到热场中作为热源数据.

如图15、16 所示为经单向磁热耦合计算得到的永磁电机的稳态温度分布图.可以看出，定子的最高温度为58.71 ℃，定子轭部的平均温度为55.04 ℃，定子齿部的平均温度为57.49 ℃.转子的最高温度为49.17 ℃，导致转子温升的原因一方面是由于转子本身的铁芯损耗而产生热量，另一方面是由永磁体涡流损耗产生的热量经热传导传递到转子.绕组的最高温度为64.91 ℃，端部绕组与槽内绕组的平均温差为4.99 ℃，原因是分布式绕组的端部较长，损耗在绕组内以及定子铁芯内传导时热阻存在差异.端部绕组与槽内绕组的对流散热系数不同，会导致温度产生差异.永磁体最高温度为47 ℃，此时的温度低于永磁体退磁温度，不会导致永磁体不可逆退磁.

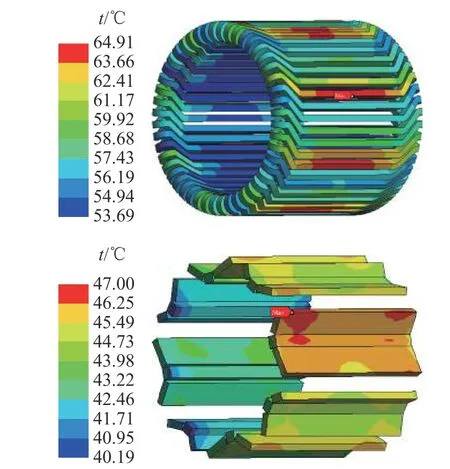
图15 利用单向磁热耦合法计算得到的绕组、永磁体温度分布Fig.15 Temperature distribution of windings and permanent magnets calculated by unidirectional magneto-thermal coupling

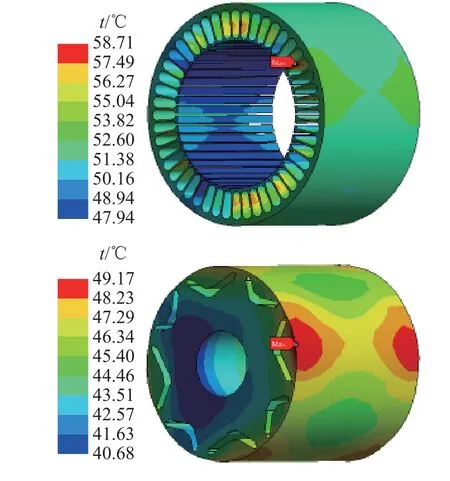
图16 利用单向磁热耦合法计算得到的定子、转子温度分布Fig.16 Temperature distribution of stator and rotor calculated by unidirectional magneto-thermal coupling

3.2 双向磁热耦合的分析

单向磁热耦合法的计算精度比集中参数热网络法高，更能够直观地得到电机各部件的温度分布，但单向磁热耦合分析未考虑温度升高对材料性能的影响，尤其是温度升高对铜线绕组电导率及永磁体性能的影响.为了进一步提高计算精度，对电机进行双向热耦合仿真，电热双向耦合流程如图17 所示.

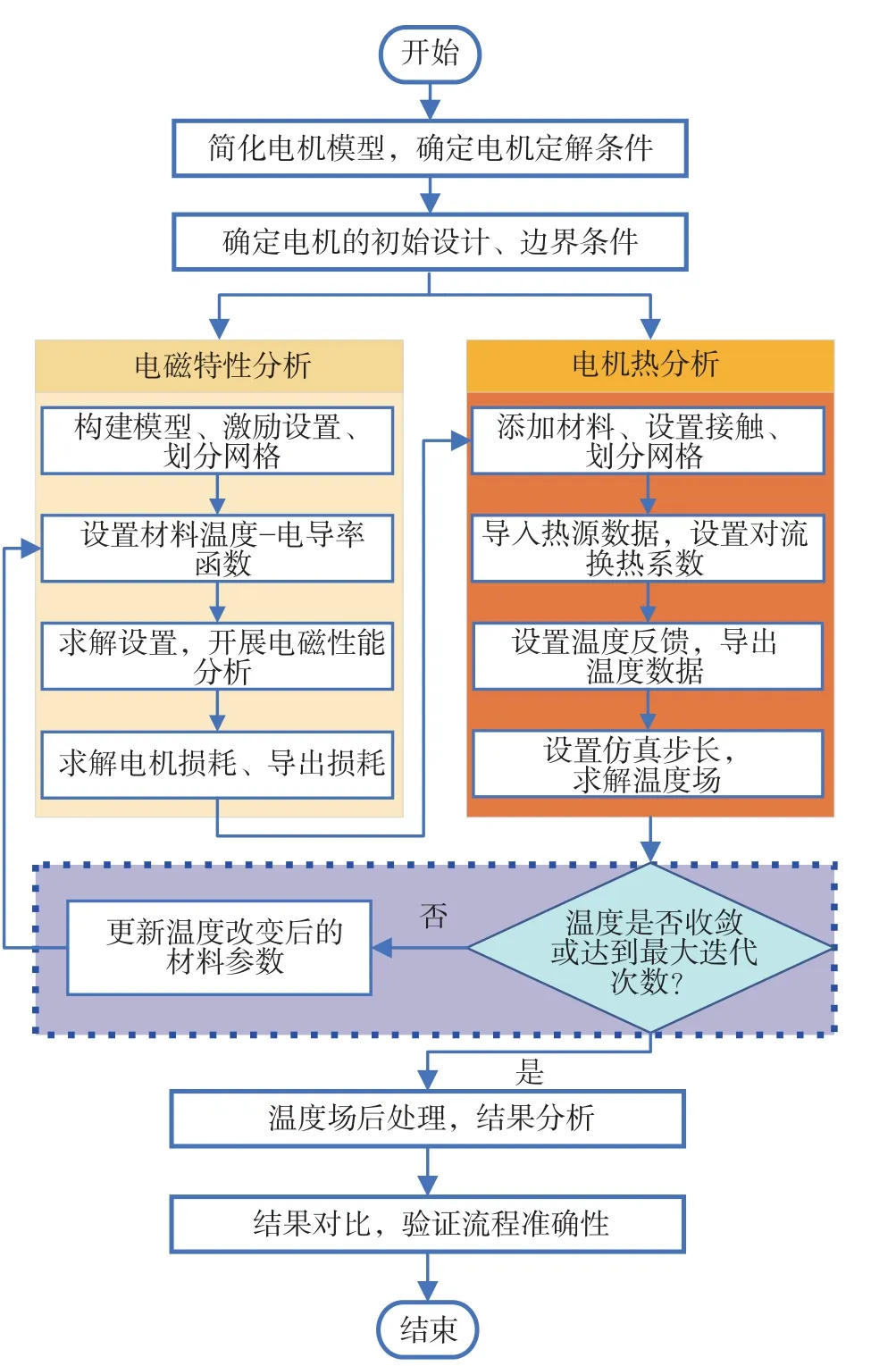
图17 双向磁热耦合的流程图Fig.17 Flow chart of bi-directional magneto-thermal coupling

与单向磁热耦合分析不同，在双向磁热耦合中，分析电机损耗时采用三维场进行计算.采用三维场进行计算，可以确保计算精度；在三维场中可以得到电流分布及绕组温度分布.与单向磁热耦合分析一致，经电磁场分析得到的电机损耗传输到热场中作为热源，在双向磁热耦合法中所设置的约束条件均与单向磁热耦合法热场中设置的约束条件一致，尽量减少无关变量的影响，保证单一变量原则.

在双向磁热耦合分析中，利用热场计算得到的温度数据会返回到电磁场中，电磁场根据返回的温度数据改变材料的电导率后再次进行计算，计算完成后将损耗数据传递到热场中形成数据的闭环传递.如此进行多次迭代计算，直至温度达到所设置的误差范围内或达到最大迭代次数.温度对铜电导率的影响为

式中：Rt为t摄氏度时的电阻，为初始温度时的电阻，为铜线的电导率温度系数.温度对永磁体性能的影响主要体现在永磁体的磁体剩磁及矫顽力：

式中：BR、HC分别为t摄氏度时的磁体剩磁、矫顽力，为初始温度时的磁体剩磁，为初始温度时的矫顽力，αbr、αhc分别为磁体剩磁及矫顽力的温度系数.

如图18、19 所示为通过双向磁热耦合分析得到的永磁电机温度分布图.可以看出，绕组的最高温度为72.71 ℃，最高温度在槽内绕组部分，端部绕组的平均温度为65.10 ℃.永磁体的最高温度为51.37 ℃，永磁体的中部温度高于永磁体的端部温度.定子的最高温度为65.21 ℃，定子轭部的平均温度为60.86 ℃，定子齿部的平均温度为63.76 ℃.转子的最高温度为53.93 ℃，气隙越小处的转子温度越高.无论是电机的整体温度还是定转子、绕组以及永磁体的温度，双向耦合仿真结果均比单向耦合仿真结果高.这是因为双向磁热耦合分析数据会在电磁场与热场之间进行多次迭代传递，且每次传递的数据都会有变化，变化的数据在电磁场中引起电机损耗的变化，在热场中导致温度产生差异.金属电导率与温度有很大的相关性.铜的电导率随着温度的升高而降低，在一定范围内，电导率可以被近似为与温度成正比.电导率的倒数为电阻率，电导率降低则电阻率升高，电阻率升高会导致电阻增大，在电流激励不变的情况下，会导致绕组铜损产生变化.

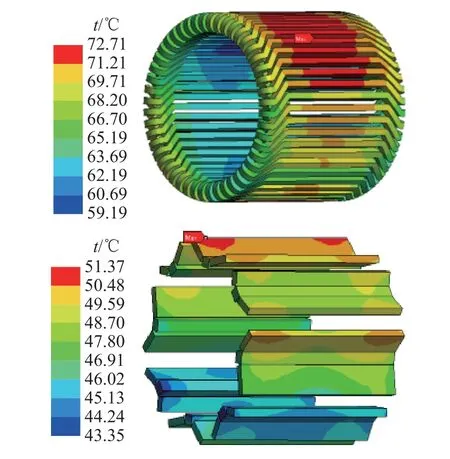
图18 利用双向磁热耦合法计算得到的绕组、永磁体温度分布Fig.18 Temperature distribution of windings and permanent magnets calculated by bi-directional magneto-thermal coupling

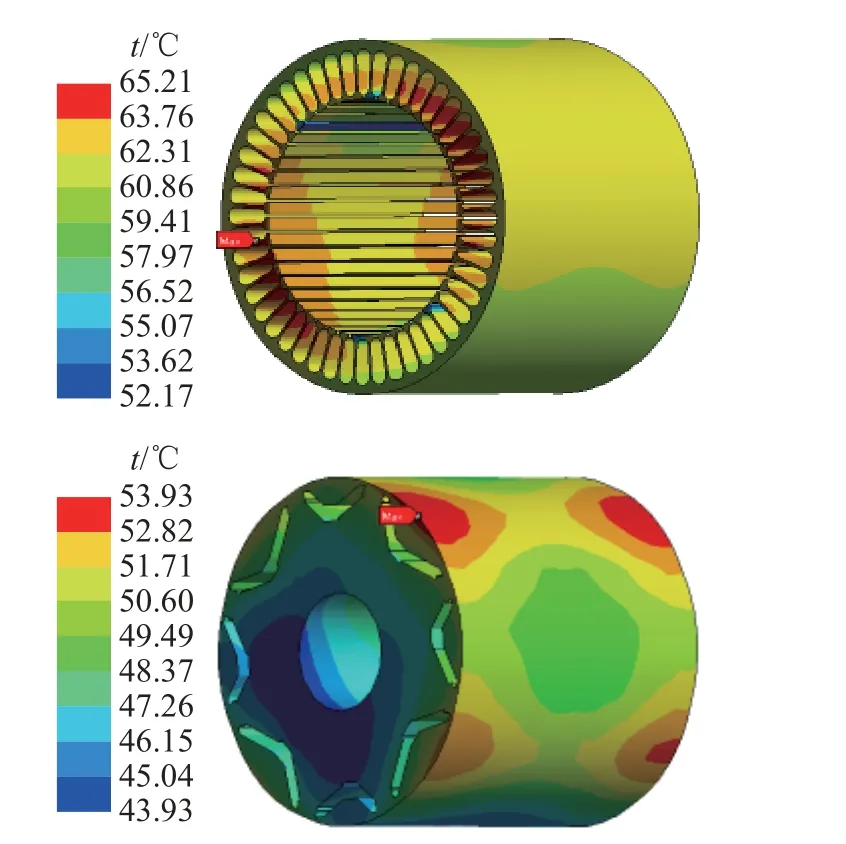
图19 利用双向磁热耦合法计算得到的定子、转子温度分布Fig.19 Temperature distribution of stator and rotor calculated by bidirectional magneto-thermal coupling

如图20 所示为在单向磁热耦合法和双向磁热耦合法计算结果下的电机输出转矩Tn比较.可以看出，利用2 种热分析法得到的电机输出转矩均有所降低，利用双向磁热耦合法仿真得到的平均输出转矩较单向磁热耦合法降低了约3.11%.

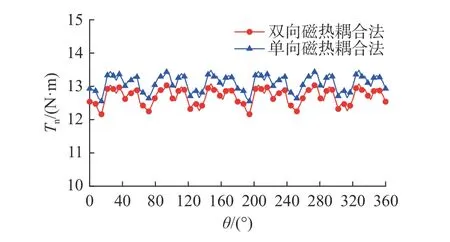
图20 单向磁热耦合法和双向磁热耦合法的输出转矩比较Fig.20 Comparison of output torque between unidirectional magneto-thermal coupling method and bi-directional magnetothermal coupling method

3.3 电枢绕组电流密度对永磁电机温升的影响分析

在保证电机电压和转速不改变的情况下，通过改变电枢绕组中的电流密度分析电机温度分布.随着电枢绕组内电流密度的升高，电机输出功率和电机损耗增大.在相同的冷却条件下，随着电枢绕组电流密度的增加，电机各部分温升如表4 所示.表中，J为电流密度，tcmax、tcavg分别为绕组最高温升、绕组平均温升，tnmax、tnavg分别为永磁体最高温升、永磁体平均温升，trmax、travg分别为转子最高温升、转子平均温升，tsmax、tsavg分别为定子最高温升、定子平均温升.通过分析可知，随着电流密度的升高，电机各部分损耗增大，电机各部分温升均升高，绕组温升的升高幅度最大.这是因为电枢绕组铜耗直接受到电流密度的影响，且电枢绕组大部分位于定子槽内，散热困难，在大功率负载下，电枢绕组的温升幅度更大.采用不同方法对电枢绕组温升进行计算，结果如图21 所示.可知，双向磁热耦合仿真结果比单向及热网络法结果高，热网络法与单向磁热耦合法的仿真结果接近.

表4 不同电流密度下利用磁热双向耦合法计算得到的非对称混合磁极永磁电机各部件温升结果Tab.4 Calculation of temperature rise of asymmetric hybrid pole permanent magnet motor components by bi-directional magnetothermal coupling under different current densities

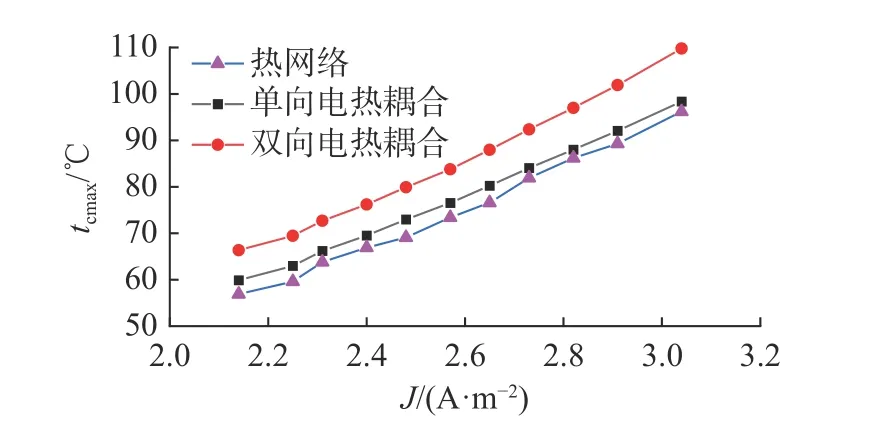
图21 不同电流密度下非对称混合磁极永磁电机的最高温升Fig.21 Maximum temperature rise of asymmetric hybrid pole permanent magnet motor under different current density

4 实验验证

为了验证提出的非对称混合磁极电机的有效性及双向磁热耦合法计算结果的准确性，试制了一台样机，如图22(a)、(b)所示.在电机电枢绕组端部及定子槽内预埋PT100 热敏电阻，搭建非对称混合磁极永磁电机的试验平台，如图22(c)、(d)所示.

图22 样机及温升实验平台Fig.22 Prototype and temperature rise experiment platform

在3 000 r/min 下，对该样机进行温升试验，样机的稳态温度t云图如图23 所示.样机温升稳定时最高温度为64.5 ℃，双向磁热耦合仿真结果中，定子的最高温升为65.21 ℃，仿真结果与实验结果吻合良好，证明了双向磁热耦合方法的准确性.电机最高温升的对比曲线如图24 所示，额定工作状态下运行时最高温升稳定在70.6 ℃左右，双向磁热耦合仿真电机的最高温升为72.71 ℃.仿真结果与试验结果的温升曲线趋势一致，最终达到稳定温度时结果相近，反映出仿真结果与实验结果吻合良好，验证了提出的拓扑结构的合理性及有效性，证明了双向磁热耦合法的准确性.

图23 稳态温度云图Fig.23 Steady state temperature cloud

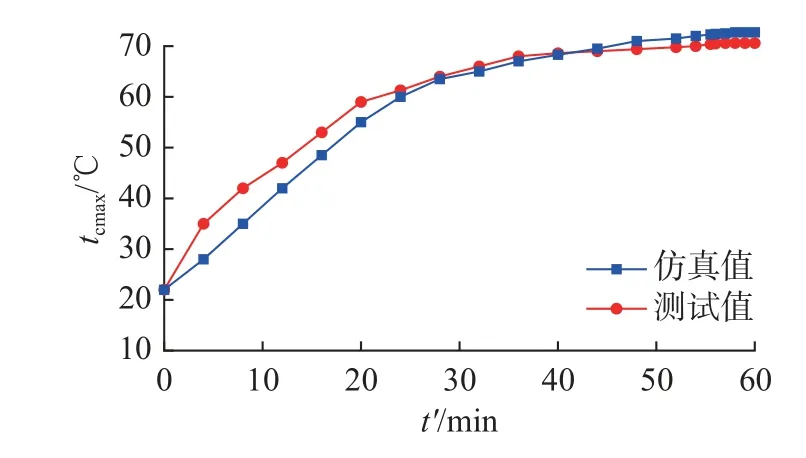
图24 电机的最高温升曲线Fig.24 Maximum temperature rise curve of motor

样机空载反电势的实验平台如图25 所示.样机固定在实验台架上由伺服电机拖动，将伺服电机的转速设定为3 000 r/min，测得的空载反电势波形如图26 所示.可以看出，测试的反电势波形具有良好的正弦性和对称性，与仿真波形具有良好的一致性.对测试反电势波形进行傅里叶分解，得到反电势畸变率(THD)，并将结果与仿真结果进行对比，如图27 所示.实测反电势THD 为6.22%，仿真结果为4.35%，这表明实测波形和仿真波形吻合良好.

图25 空载反电势的实验平台Fig.25 Experimental platform of no-load back EMF

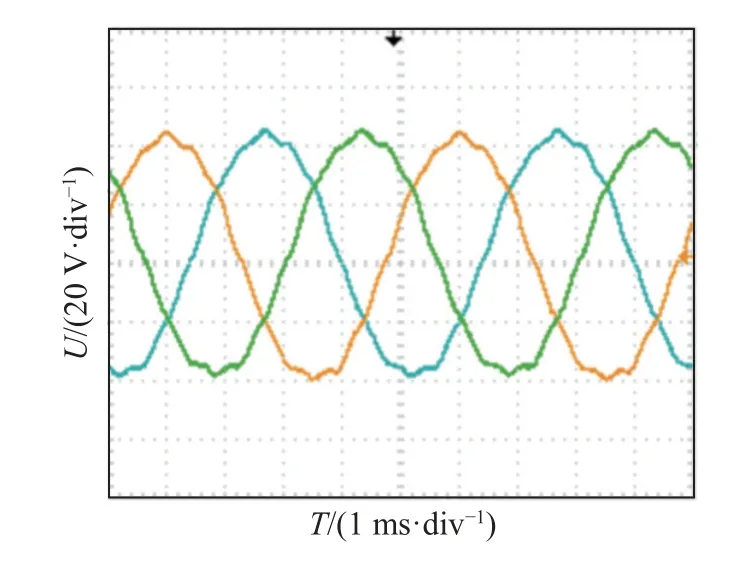
图26 实测空载反电势的波形Fig.26 Waveform of measured no-load back EMF

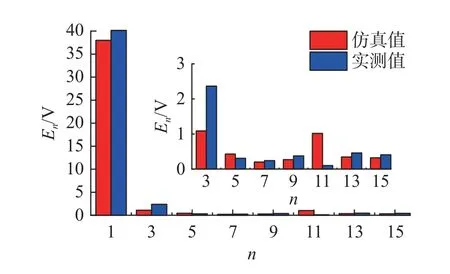
图27 空载反电势波形THDFig.27 THD of no-load back EMF

5 结论

(1) 与传统内置式永磁电机相比，非对称混合磁极永磁电机的涡流损耗降低了29.26%，铁芯损耗降低了18.41%，额定转速下的总损耗降低了21.79%.非对称混合磁极永磁电机具有更高的输出能力和工作可靠性.

(2)非对称混合磁极永磁电机采用非均匀气隙结构、永磁体分段以及采用铁氧体替代部分永磁体的拓扑结构，使得气隙磁通密度幅值提升了12.85%，反电势波形THD 由传统内置式电机的9.97%降低至4.35%，因此非对称混合磁极永磁电机能够有效地降低电机损耗.

(3)当不考虑温度对电机材料电导率的影响时，利用等效热网络法能够快速地准确计算电机温升，计算结果与单向磁热耦合结果接近.当考虑温度对材料的影响时，双向磁热耦合法的计算结果更接近实验结果.