大点数FFT 在“申威26010”上的并行优化

郭俊，刘鹏，杨昕遥，张鲁飞，吴东

(1.湖州职业技术学院 信息工程与物联网学院，浙江 湖州 313000；2.湖州职业技术学院 湖州市物联网智能系统集成技术重点实验室，浙江 湖州 313000；3.浙江大学 信息与电子工程学院，浙江 杭州 310027；4.蚂蚁科技集团股份有限公司，浙江 杭州 310013；5.数学工程与先进计算国家重点实验室，江苏 无锡 214125)

随着数字计算机和超大规模集成电路的飞速发展，数字信号处理技术得到了越来越广泛的应用，快速傅里叶变换（fast Fourier transform，FFT）是其中最基本、使用最频繁的核心算法之一.其他诸多信号处理算法，例如卷积、滤波、频谱分析等，都可以转化为FFT 来实现.

超级计算机为解决当今海量级数据的科学与工程计算问题提供了良好的平台.“神威·太湖之光”是世界上首台峰值每秒浮点运算次数（FLOPs）超过100×1015的超级计算机，也是中国第一台全部采用自主技术构建的排名世界第一的超级计算机[1].“神威·太湖之光”由国产“申威26010”处理器组成，单处理器峰值FLOPs 可达3.1×1012.相比之下，访存带宽仅有136.5 GB/s 则略显逊色，计算访存比接近22.7.在面对诸如FFT 这样兼具计算密集型和访存密集型特点的程序时，需要设计特定的并行实现策略，以优化其性能.

本文的主要工作是根据“申威26010”处理器的架构特点和编程规范，提出针对大点数FFT 的众核优化方案.该方案源自经典的Cooley-Tukey FFT 算法，将一维数据迭代分解为二维FFT 进行加速.为了解决“列FFT”的读写和计算问题，降低矩阵转置的影响，提出“列均分-行连续”结合DMA跨步传输的读写策略.该方法还可以推广至其他需要进行大量列数据操作的应用.计算部分采用旋转因子优化和向量化操作，传输部分采用双缓冲策略和寄存器通信，能够充分利用众核系统的计算资源和传输带宽，达到了良好的加速效果.

1 相关工作及研究现状

1.1 快速傅里叶变换

FFT 是离散傅里叶变换（discrete Fourier transform，DFT）的快速算法，由Cooley 等[2]提出，经过近60 年的发展，形成了庞大的算法体系，陆续衍生出包括高基[3]、混合基[4]、分裂基[5]、多维度[6]等多种FFT 算法，以应对各种数据类型和数据量.

在具体实现方面，FFT 的硬件优化主要针对FPGA、ASIC、DSP 等专用处理器，大致可以分为基于存储器和基于流水线2 类.基于存储器的结构利用数据在计算单元和存储单元之间往复运算和循环路由的特征来降低硬件复杂度[7-8].基于流水线的结构通过设计单路/多路的前馈/反馈路径，提升蝶形单元的吞吐率[9-10].

FFT 的软件优化主要是通用平台上高性能软件包（库）的开发.常见的有CPU 平台上Frigo 等[11]开发的FFTW、Intel 公司[12]的MKL FFTW 等、GPU平台上NVIDIA 公司[13]的CUFFT、Ayala 等[14]提出的heFFTe 等.其中，FFTW 是目前使用最广泛、综合性能较好的FFT 库.张明[15]在龙芯3B 处理器上、郭金鑫[16]在ARM V8 平台上、操庐宁[17]在X86-64 平台上均对FFTW 库进行了移植和优化.

1.2 申威26010 与神威·太湖之光

国产“申威26010”处理器由上海高性能集成电路设计中心通过自主技术研制，采用片上计算阵列集群和分布式共享存储相结合的异构众核体系架构，使用64 位自主申威指令系统.单芯片集成了4 个核组共260 个核心，每个核组包含1 个控制核心（主核）和由64 个运算核心（从核）组成的核心阵列.如图1（a）所示为处理器的结构示意图，如图1（b）所示为从核与主存、局存、寄存器之间的简化通信模型.在编程规范上，核组内部采用Athread 多线程库或OpenACC 并行编程，核组间使用MPI 或OpenMP 编程接口.新一代“申威26010-Pro”处理器于2021 年发布，单核组运算性能和访存带宽分别提升了3.1 倍和1.8 倍.

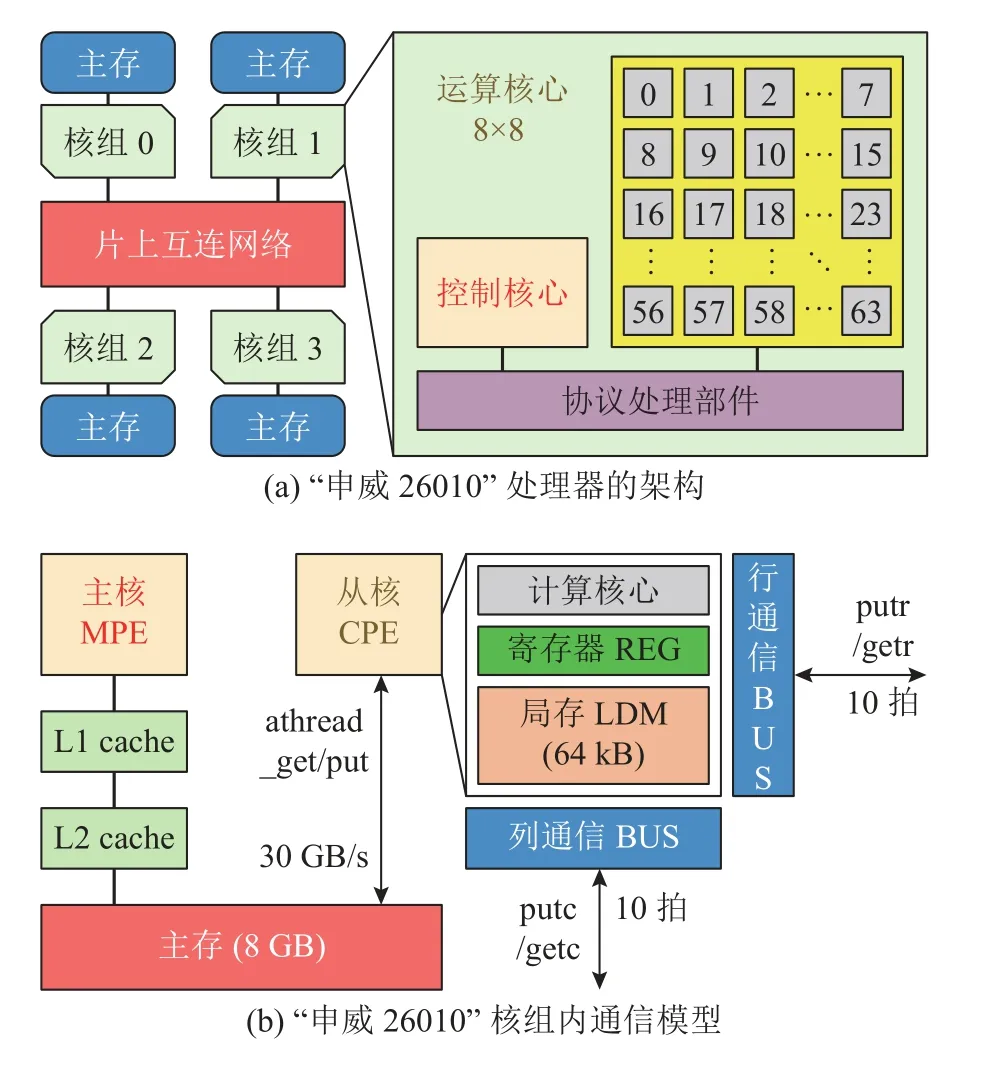
图1 “申威26010”处理器的示意图Fig.1 Schematic of Sunway 26010 processor

“神威·太湖之光”由中国国家并行计算机工程技术研究中心于2015 年12 月完成研制，投入运行，已成功解决众多的科学工程计算问题.目前已升级为配备有“申威26010-Pro”处理器的新一代超算系统.代表性应用包括Yang 等[18]的“千万核可扩展大气动力学全隐式模拟”、Fu 等[19]的“非线性地震模拟”、Liu 等[20]的“超大规模量子随机电路实时模拟”等，分别于2016 年、2017 年、2021 年三度荣获“戈登贝尔奖”.

在“神威·太湖之光”上开发了高性能扩展数学库xMath 并移植了FFTW 库，其中面向科学计算BLAS 库的优化已十分成熟[21-22]，但是缺少针对FFT 的研究.赵玉文等[23]在“申威26010”上实现了迭代Stockham FFT 计算框架，与单主核FFTW相比，获得了平均44.5x、最高56.3x 的加速比.Stockham FFT 是Cooley-Tukey FFT 的一种常见变化算法，主要特点是消除了输入输出的倒位排序，可以避免传统FFT 算法中的显式转置，在大数据量下能够实现一定的性能提升，代价是失去了蝶形结构的对称性和原位计算的特征，迭代框架的实现相对比较复杂.

针对FFT 优化的开发需求，根据“申威26010”处理器的架构特点与FFT 算法的内在联系，提出“列均分-行连续”读写策略.结合其他优化手段，对数据进行巧妙的划分、重排和交换，可以减少行列转置带来的影响，完成了经典Cooley-Tukey FFT 的众核实现，达到了大点数下平均60x 以上的加速比.

2 大点数FFT 算法

离散傅里叶变换DFT 的计算公式为

FFT 作为DFT 的快速算法，核心思想是将长输入逐次分解成短序列DFT进行递归计算，通过分而治之的策略，将计算复杂度降至O(Nlog2N).大点数FFT 的加速算法沿用了上述思想，通过将一维数据转化为二维或更高维，减少了每一维上的数据量，更有利于进行多核/众核并行.

将输入规模为N=N1×N2的一维数组映射为N1行、N2列的二维矩阵.令输入、输出序号为

其中，0 ≤n1、k1≤N1-1，0 ≤n2、k2≤N2-1.有如下关系：

一维转二维FFT 的计算流程（见图2）如下.

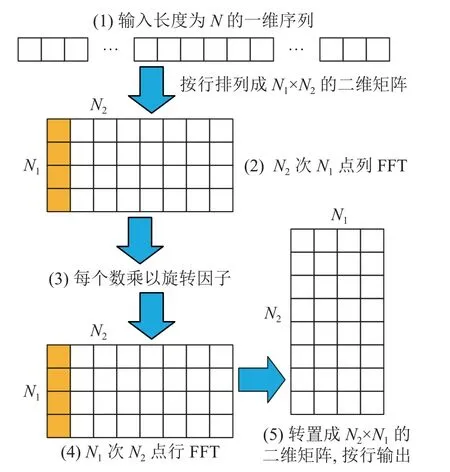
图2 一维转二维FFT 的计算流程Fig.2 Calculation process of 1D to 2D FFT

1）将一维数据按行优先顺序排列为N1行、N2列的二维矩阵.

2）进行每一列N1点 FFT，共进行N2次，按原位置存回.

3）对于矩阵中的每一个数据，根据其坐标，乘以旋转因子 e xp(-j2πn2k1/N).

4）进行每一行N2点FFT，共进行N1次，按原位置存回.

5）按列优先顺序将数据读出，得到N=N2N1的最终结果.

3 大点数FFT 在“申威26010”上的并行优化

将大点数FFT 在“申威26010”上并行实现时，主要面临如下难题.1）主核与从核之间列数据的读写问题.2）从核间行列数据的分布与转置问题.3）从核内小点数FFT 的高效实现问题.

下面给出具体的并行优化解决方案.

3.1 基本存储和分解策略

使用双精度浮点复数，包括8 B 的实部和8 B 的虚部.“申威26010”从核对局存LDM 的访问延迟为4 个CPU 周期，仅为对主存访问延迟的1/40，应尽可能将主存中的数据放入LDM 内再计算.考虑到单从核LDM 大小仅为64 kB，采用双缓冲策略需要2 份输入/输出缓冲区（3.6 节），将可单次写入LDM 的最大数据量规定为512 个复数.输入和输出共占512×16×2×2=32 kB，余下一半空间存储中间结果和临时变量.

“申威26010”单个核组阵列包括8 行8 列共64 个运算核心.为了方便维度分解和FFT 计算，总数据量采用2 的正整数幂次，每一维上的最小尺寸设置为8.下面给出基本的分解策略.

1）将总点数分解为N=N1N2，通常N1和N2较大，需要继续分解.以N1为例，可以按以下a）、b）、c）共3 种情况进行分解.

a）N1＜64，即8、16、32 点，停止分解，直接在单核上进行小点数FFT 计算.

b）64 ≤N1≤256，将N1进行二维分解，包括8×8、16×8、32×8 共3 种方案.前一位数（8、16、32）代表单核上的FFT 点数，后一位数（8）代表启动一行（或一列）8 个从核进行计算.

c）512 ≤N1≤2 048，将N1进行三维分解，包括8×8×8、16×8×8、32×8×8 共3 种方案.前一位数（8、16、32）代表单核上的FFT 点数，后两位数（8×8）代表启动64 个从核进行计算.

2）同理，N2按以上3 条进行再分解.当N1、N2≥4 096 时，对总点数N进行三维及以上分解，并启动多个核组.

3）每多分解一次，需要将当前FFT 替换为图2所示的“列FFT-乘旋转因子-行FFT”流程，直至迭代计算完毕.

下面以输入数据量为262 144=512×512 的实例，阐述各创新实现技术.

3.2 “列均分-行连续”策略

在行优先的存储系统中，对列数据的读写是离散非连续的，传输效率很低.一维转二维FFT并行方案的主要难点是对矩阵“列FFT”的处理.大数据量加剧了FFT 访存密集型特点带来的上述影响，若在主核上先进行显式转置再传输，则会增加不可忽略的额外开销.

为了提升“列FFT”的并行效率，结合FFT 算法、处理器架构以及数据在从核间的分布特点，提出“列均分-行连续”读写策略，即并非用单个从核去读取主存中的列数据，而是把每一列的数据循环平分给64 个从核.如图3 所示，对于“大矩阵”的每一列，0 号核读第0 行，1 号核读第1 行，······，63 号核读第63 行.然后0 号核读第64 行，······，直至63 号核读第511 行.从列的方向来看，每一列循环平分到64 个从核内.每个核一次可以读取多列，从行的方向来看，数据是连续读取的，即为“列均分-行连续”策略.

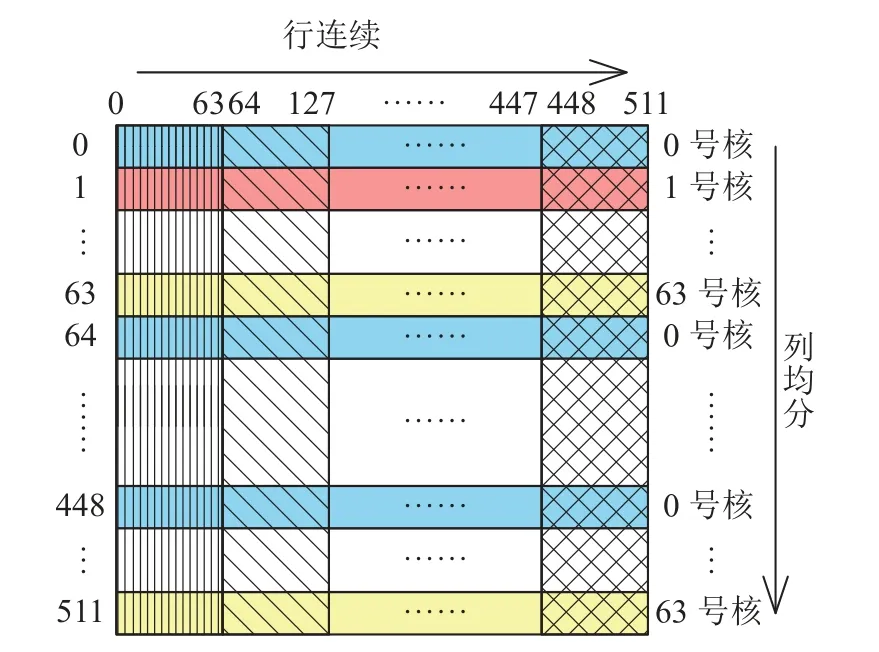
图3 “列均分-行连续”策略Fig.3 Column-sharing,row-continuity strategy

每个从核分到512/64=8 行的数据.由于LDM最大单次输入量为512，可以连续读入“大矩阵”每一行中512/8=64 个数.由于“申威26010”主存与局存之间的DMA 带宽性能在传输粒度≥256 B（32 个double 数据）时达到峰值，采用“列均分-行连续”策略的第1 个优点，即在保证一列数据能够完整读入从核阵列的同时，符合行优先的存储结构，且充分利用了传输带宽，从而有效解决了列读写的不连续性.

3.3 从核间数据分布与寄存器通信转置

“列均分-行连续”策略的第2 个优点，即从核间的数据分布与大点数分解方案吻合，有利于“列FFT”的后续计算.如图4 所示为“大矩阵”列数据在从核间的分布，方格中的数字代表该数据所在的从核号.将“大矩阵”任意一列512 个数（见图4（a））排列成64×8 的“中矩阵”（见图4（b）），再将“中矩阵”的任意一列继续转换成8×8 的“小矩阵”（图4（c）以图4（b）中的第0 列为例）.此时，“小矩阵”中的每一列数据均保存在同一个从核中，因此可以直接计算“小矩阵”“列FFT”.

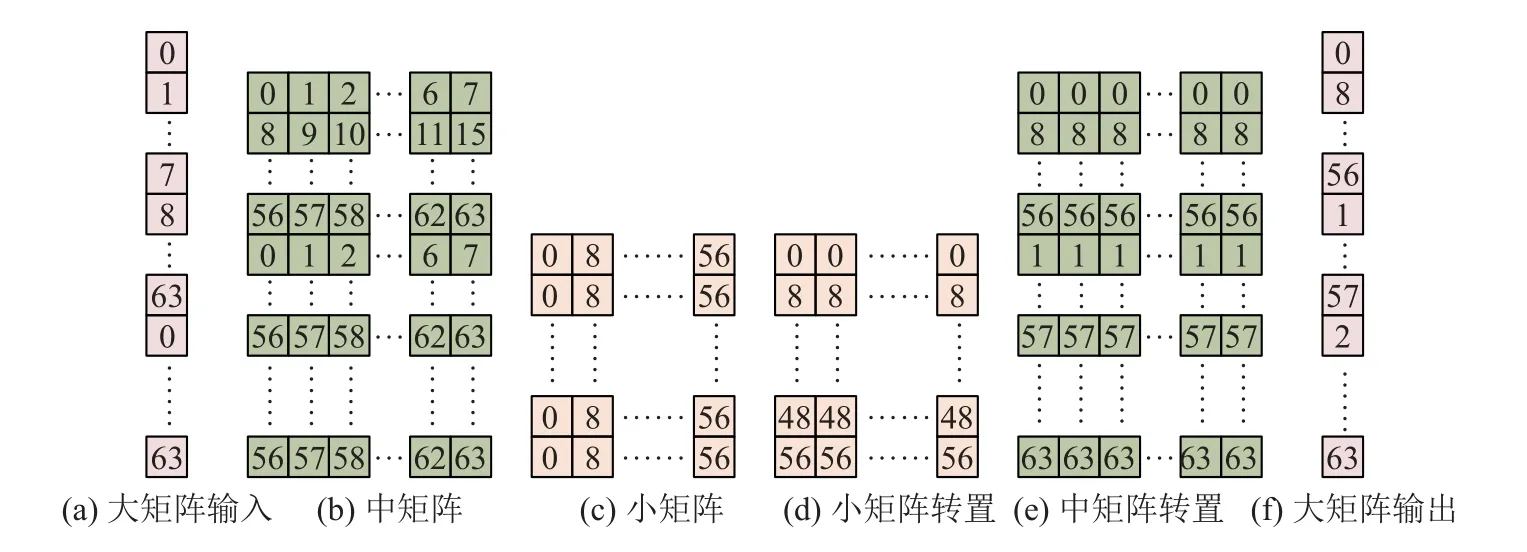
图4 从核数据分布Fig.4 Data distribution among slave cores

图4（c）中，“小矩阵”的每一行数据分散在同列8 个从核中，可以利用“申威26010”的寄存器通信机制来实现从核间的数据交换.使用putc 和getc 指令开启寄存器列通信模式，同列8 个核之间彼此将各行数据传到对应的从核，并接收其他从核传给自己的数据，即可完成“小矩阵”的列与行转置（见图4（d）），继续执行“小矩阵”“行FFT”计算.在“小矩阵”FFT 计算完毕后，核间数据按图4（d）中的列优先顺序排列，实际上与图4（b）保持一致.“中矩阵”的转置过程与“小矩阵”类似，但须使用putr 和getr 指令开启寄存器行通信模式（见图4（e））.在完成“中矩阵”FFT 后，将数据按列优先顺序写回主存（见图4（f））.LDM 内的64 列数据均按图4（f）的顺序排列，因此写回过程符合“列均分-行连续”原则，DMA 传输可达最大速度.

3.4 SIMD FFT

FFT 计算采用单指令多数据流操作（single instruction multiple data，SIMD）进行加速.“申威26010”支持宽度为4 个double 数据的向量运算（doublev4），但须解决以下2 个问题.1）若将同组FFT 数据放在一个向量内，则不同间距的蝶形会引起数据依赖问题（见图5（a））.2）若分散在不同向量内，则离散数据装载/卸载向量的效率较低.

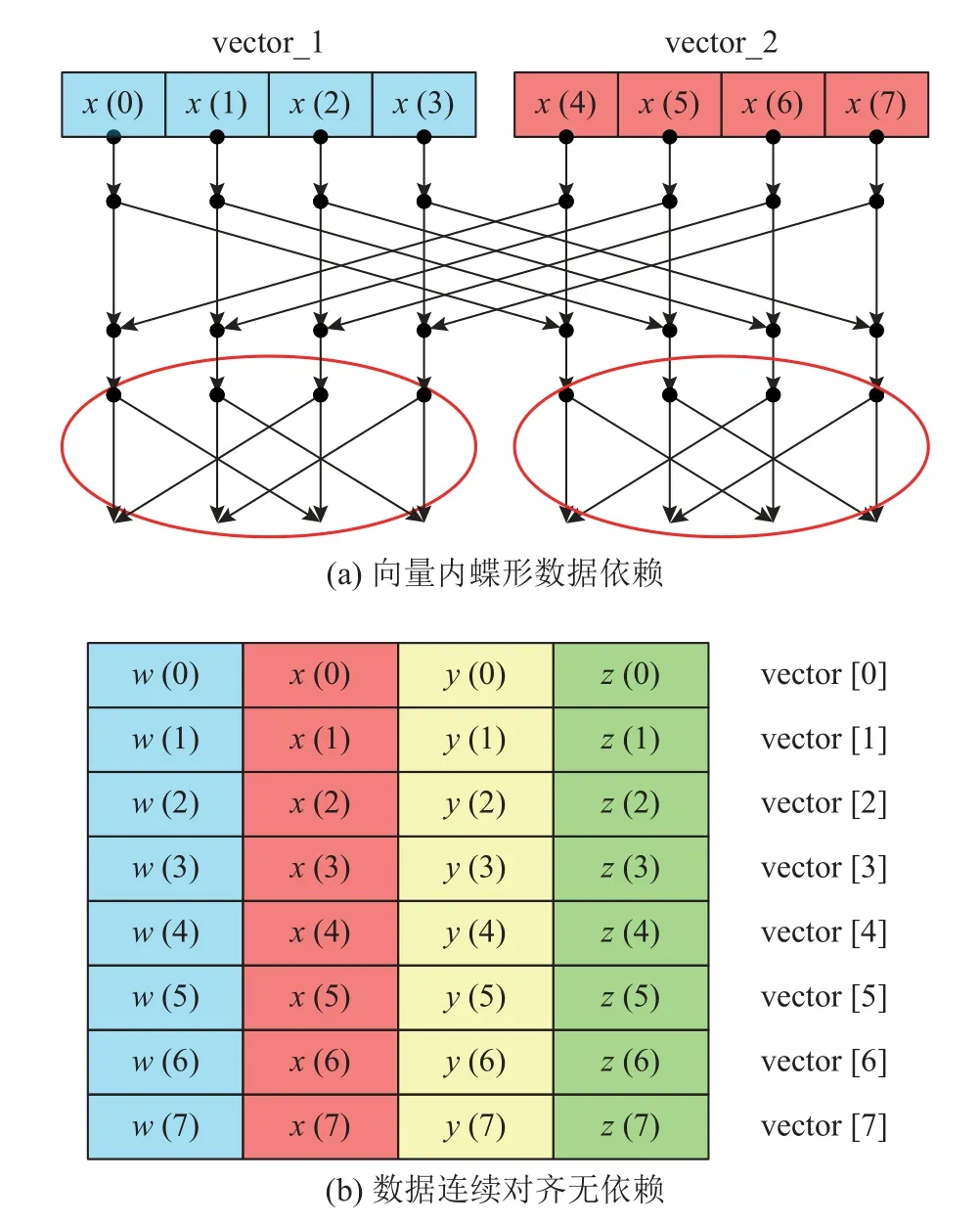
图5 SIMD FFT 数据排列Fig.5 SIMD FFT data arrangement

当前每个从核LDM 内的数据排列为8×64 的矩阵，行方向上为从“大矩阵”中读入的一行64 个数据（见图3），列方向上是“小矩阵”中一列（行）（见图4（c）、（d））或“中矩阵”中一行（见图4（e））的8 个数据.采用doublev4 数组进行装载，每个doublev4 内的4 个子元素互不相关，不同doublev4内相同位置上的子元素来自同一组FFT 数据，如图5（b）所示，既消除了向量内数据依赖，可以一次完成4 组FFT 计算，又使得数据在LDM 内的存储连续且边界对齐，向量的装载和卸载效率最高.这是“列均分-行连续”策略的第3 个优点.

3.5 旋转因子计算优化

1）和差化积.所有旋转因子系数均为2 π/N的nk倍（N为矩阵规模，n和k为坐标）.对基本单元cos(2π/N) 和 sin(2π/N) 使用和差化积，用复数乘法代替三角函数，大幅减少三角函数的调用次数.

2）数据复用.每个从核读入的“大矩阵”多列数据，实际上每一列在图4 所示的“小矩阵”和“中矩阵”中所处的位置都是一样的，即坐标相同，因此只须计算第1 列旋转因子并复用.

3）提前计算.所有的旋转因子均由矩阵尺寸，即输入数据量决定，可以提前完成计算.和差化积缩短了计算时间，数据复用减少了计算次数，将旋转因子计算与第一次DMA 传输同步进行，不会给存储空间和计算时间带来额外负担.

此外，所有旋转因子的计算和相乘采用SIMD操作，可以与FFT 结合.

3.6 双缓冲策略和跨步读写

“申威26010”为异步DMA 传输，当数据需要在主存与局存之间进行多次传输时，可以采用双缓冲策略.如图6 所示，数字表示循环轮次，奇数轮和偶数轮分别占用2 份不同的输入/输出缓冲区.可以看出，除了第1 轮读入和最后1 轮写回外，在进行中间轮次计算的同时，可以进行下一轮读入及上一轮写回，以计算时间隐藏通信开销.

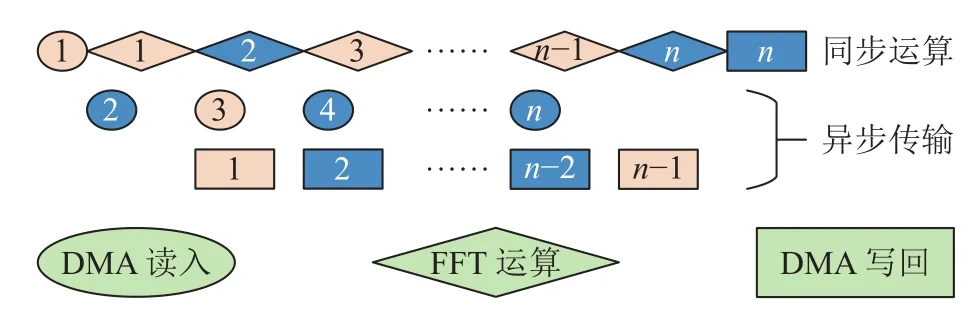
图6 双缓冲机制Fig.6 Double buffering scheme

实际上，DMA 还包括启动athread_get（读入）和athread_put（写回）的函数调用开销.该步骤为串行过程，无法被计算隐藏，当一次完整读写需要多次调用这2 个函数时，耗时不可忽略.从核在每一轮“列均分”中共分到8 行数据，须调用get和put 函数各16 次（实部和虚部各1 次），因此无法被双缓冲隐藏的DMA 时长T=16T1（设T1为函数调用时间），导致加速提升不到10%.

此时，每个从核在主存上的访问空间呈现等数据量（行连续）、等间隔（列均分）的特点（见图4（a）、（f））.通过配置athread_get(dma_mode mode,void *src,void *dest,int len,void *reply,char mask,int stride,int bsize)的最后2 个参数“间距”和“单次传输数据量”，可以实现跨步传输.跨步读写仅须调用get 和put 各2 次，无法隐藏的调用时间2T3＜＜16T1（设T3为跨步函数调用时间），达到了非常明显的加速效果.

3.7 FFT 完整流程

如图7 所示为“大矩阵”“列FFT”的完整计算流程，包括各环节采用的优化方法.“大矩阵”“行FFT”的计算过程与“列FFT”类似，此处不再赘述.

4 实验结果与分析

4.1 实验运行环境

测试了数据量为32 768～4 194 304 共8 组随机生成的双精度浮点复数.众核并行程序启用“申威26010”1 个核组共64 个从核，运行时间从athread_spawn 开始至athread_join 结束，包括传输和计算全过程.对比基准为单主核上运行FFTW 3.3.4库以最优plan 计算相同输入的用时，仅统计fftw_execute 计算时间.所有实验均重复多次，取稳定值求平均作为测试结果.

4.2 各优化策略的加速效果

如图8 所示为采用旋转因子优化、SIMD、双缓冲以及改用跨步传输后再结合双缓冲等各方案的加速比SP.

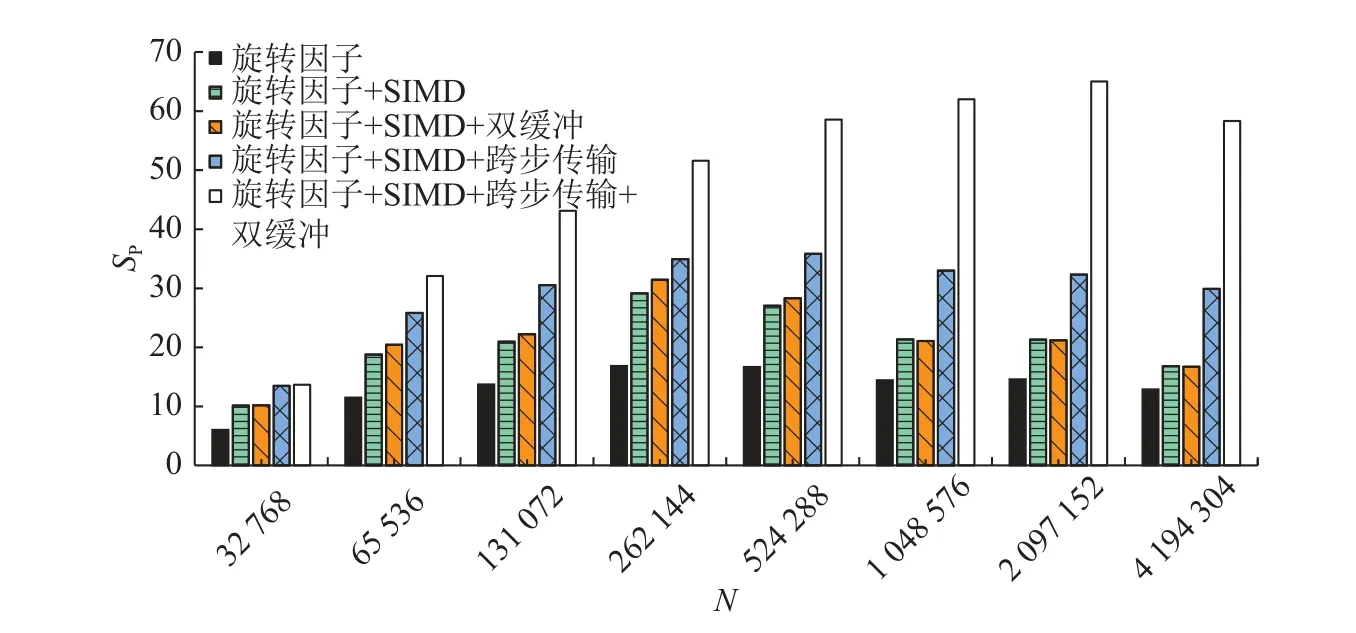
图8 采用旋转因子优化、SIMD、跨步传输、双缓冲方案的加速比Fig.8 Speedup using twiddle factor optimization,SIMD,stride transmission,double-buffering scheme

4.2.1 计算环节 如表1 所示为优化前、后单个从核内旋转因子的计算量.其中，小点数FFT 所需的旋转因子数量分别为4、8、16，可以一次完成计算，所以忽略不计，只统计一维转二维方案中“列FFT”转“行FFT”之间所须乘上的旋转因子.3.5 节优化策略的核心思想是以和差化积所需的复数乘法和加法（或4 次实数乘法和2 次实数加法）来代替耗时较长的三角函数调用.以262 144=512×512 为例，优化前需要40 960 次三角函数，优化后仅为24 次三角函数加上1 136 次浮点运算.且该加速效果随着计算规模的增大而提高.

表1 旋转因子优化前、后的计算次数Tab.1 Calculation times of twiddle factor before and after optimization

实验结果表明，若未对旋转因子计算进行优化，则多核并行总耗时比单主核FFTW 长，而通过3.5 节所述的和差化积、数据复用、提前计算等优化策略，可以达到15 倍左右的加速比.因此，旋转因子优化可以认为是计算环节中必须且最主要的加速部分.

在加入SIMD 向量化运算后，可以在旋转因子优化的基础上提升近2 倍的加速效果.SIMD 覆盖了计算环节的几乎所有部分，包括FFT 以及旋转因子相乘.若单独测量运算部分，则可以达到约3.5 倍的加速，接近4 倍峰值，证明利用3.4 节的方案，降低了装载/卸载向量引起的额外开销.

4.2.2 通信环节 从核间寄存器单点通信的标称延迟为10 拍，但是在应用中通常会叠加put/get 指令执行开销、显式sync 同步开销、网络堵塞延迟、连续读写延迟等，效率明显降低，需要采用汇编级流水线优化进行手动提升.在本实验中，每次寄存器通信共须传输512×7/8=448 个数，数量固定，因此耗时基本稳定，优于采用DMA 传回主存，且改用DMA 传输后会导致计算时间无法覆盖传输时间，使双缓冲失效.寄存器通信是“小/中矩阵”“列/行”转置的首选方案.

在“列均分-行连续”策略中，直接采用双缓冲，加速比最大提升不到10%.与get 和put 调用次数有关，数据量越大，调用次数越多，双缓冲效果越差.在改用跨步传输再加上双缓冲后，达到了非常明显的加速效果，大数据量时可以再提升1 倍以上，与3.6 节的传输过程分析基本吻合.

如图9 所示为不同输入点数时的DMA 平均传输带宽BW及利用率UBW统计.可以看出，“行连续”策略能够保证连续传输字节数≥256 B，因此可以在大多数情况下保持对读写带宽的充分利用.当仅在最大数据量分解方案为2 048 列时，连续读写粒度减小为128 B，导致性能下降.以实测读带宽峰值27.9 GB/s 进行折算，带宽利用率最高可达89.6%，最低为61.6%，平均为79.8%.

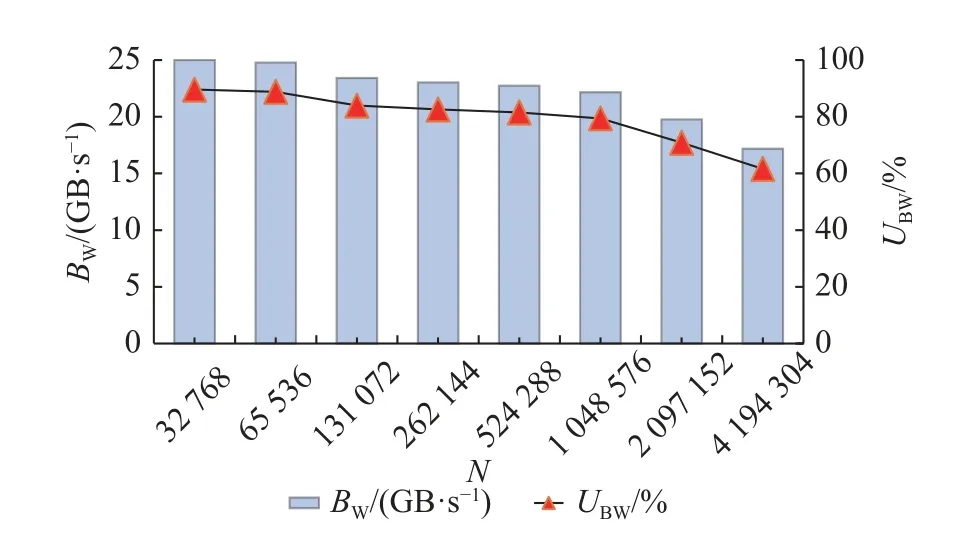
图9 DMA 传输带宽及利用率Fig.9 DMA transmission bandwidth and utilization

如图10 所示为“主-从核DMA 通信”、“从核间寄存器通信”、“从核FFT 计算”3 个环节各自在总时长中的占比TP，左边为普通传输，右边为跨步读写（图例仅表示各部分功能的相对占比关系，不表示运行时长的绝对数值）.可以看出，跨步传输+双缓冲策略使得主/从核间DMA 传输时长占比明显下降，不再是整体性能的瓶颈，各环节耗时更均衡.

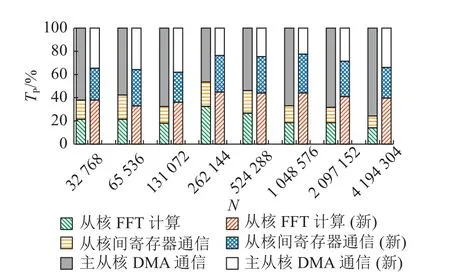
图10 传输和计算各部分功能的耗时占比Fig.10 Proportion of time consumed by transmission and calculation

4.2.3 实验小结 表2 给出FFTW 串行程序和最终多核并行方案各自的运行拍数CS、CP及两者的加速比测试结果，可以得到以下结论.

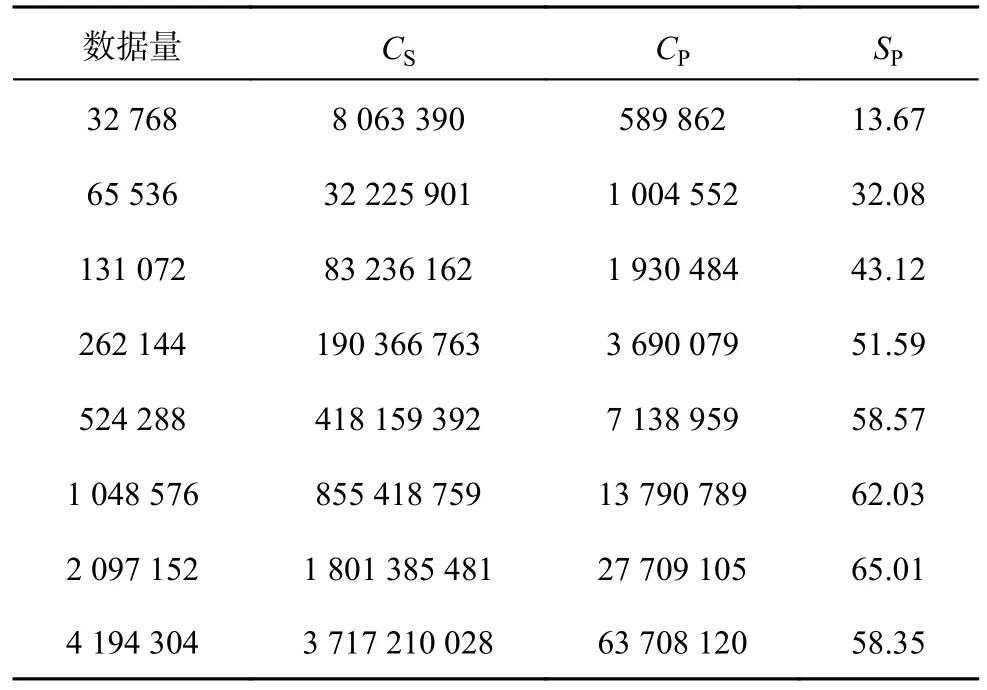
表2 并行FFT 的加速测试结果Tab.2 Accelerated test results of parallel FFT

1）该并行优化方案的核心是“列均分-行连续”策略，优点如下.a）列数据读写连续非离散，能够充分利用DMA 带宽.b）数据在从核间的分布能够直接进行后续FFT.c）数据在从核内的排列可以实现高效的SIMD.d）有助于旋转因子的快速运算.以上4 点保证了除必需的主存和局存之间的数据读写以及算法中的矩阵“列/行转置”操作以外，计算过程中基本没有额外的数据搬移，最大程度上减少了数据移动的次数，有效消除了FFT 访存密集型特点带来的影响.

2）“列均分-行连续”策略的不足，即需要多次调用读写函数而带来的开销，可以采用跨步传输+双缓冲进行弥补.合理的跨步传输能够有效地减少传输次数，从而提高异步传输时间在DMA总耗时中的占比，再利用双缓冲加以隐藏，有利于“列均分”策略的实施.

3）随着输入数据量的成倍增长，多核并行总时长的增加倍数与计算数据量的增长倍数基本相当，DMA 传输粒度保持在256 B 及以上.测试结果显示，浮点运算性能及主、从核间的传输带宽基本可以达到并维持在峰值.

4）单主核FFTW 在数据量较小时的运算性能较好，在数据量大于262 144 之后基本保持成倍增长，应该是FFTW 在不同数据量下会选择不同的最优算法所致.

5）本实验最终的加速比可以达到平均48x、最高65x 以上的出色效果，尤其是在大点数情况下，能够始终保持在50x 以上，平均接近60x.

6）利用“列均分-行连续+跨步传输”的策略，能够有效解决主、从核间“列”数据的读写问题，在矩阵应用场景下可以消除显式转置带来的影响，起到良好的加速效果.在新一代“申威26010-Pro”处理器架构中，LDM 扩大至256 kB，单次可传输数据量增加，更有利于DMA 带宽的充分利用.从核间的寄存器传输改为RMA 通信机制，性能得到进一步的提升.本方法重点关注处理器架构与算法的内在适配性，无须对软件算法框架进行大幅调整，因此可以作为一种通用优化策略进行推广使用，为“申威26010”高性能数学库中针对FFT算法的并行优化做出一定的贡献.

5 结语

本文介绍了在国产“申威26010”众核处理器上对大点数FFT 进行并行加速的方案.为了有效地解决二维FFT 对列数据的读写和计算问题，消除矩阵转置带来的影响，特别提出“列均分-行连续”的读写策略，结合SIMD 向量操作、寄存器通信转置、旋转因子优化、双缓冲+跨步传输策略等优化方法，实现了经典Cooley-Tukey FFT 算法在“申威26010”上的众核优化.与单主核FFTW 相比，可以达到平均48x 以上、峰值65x 以上的加速比.