地铁车轮不圆度控制方案分析

李哲豪

(中铁第一勘察设计院集团有限公司,陕西 西安 710043)

车轮不圆度是指列车在运行过程中,由于车轮所受的非均匀磨耗而造成的车轮多边形现象。车轮的多边形现象会导致轮轨接触过程中出现异常振动[1],异常振动又会使车轮非均匀磨耗加剧,最终,轻则导致列车运行时乘客的乘坐舒适度下降,重则导致列车脱轨,危及乘客生命安全。随着城市人口不断增长,地铁凭借其超高的运量及较高的运营速度,逐渐成为市民出行的主要交通工具,与此同时,车辆振动问题也引起了越来越多的关注,为抑制车辆的异常振动现象,对地铁车轮不圆度进行控制迫在眉睫[2]。

车轮不圆度的阶次表示车轮多边形的数量,车轮1阶不圆度指车轮出现偏心,2阶不圆度指车轮出现椭圆,以此类推[3],车轮不圆度阶次越高,对应车轮多边形的边数越多。本文针对车轮的5～7阶不圆度现象,采用“两刀镟”方案进行控制,跟踪测试结果显示,该控制方案效果良好,为地铁实际运行时的车轮不圆度控制提供了参考依据[4]。

1 车辆异常振动原因分析

1.1 车辆振动测试及分析

为探究车辆异常振动原因,镟修前,在车辆的轴箱位置处安装振动加速度传感器,测量轴箱振动加速度,传感器量程±50g。测试过程中,车辆启动加速至70 km/h,并在匀速行驶一段时间后,减速至停止。在这一过程中,采集轴箱的垂向振动加速度数据,并对采集的振动加速度进行时频特性分析,即将采集的时域数据按时间区间(时间区间长度取1 s)分成多段,分别对各段数据做傅里叶变换。为防止能量泄漏,在进行傅里叶变换前,对时间信号施加汉宁窗。傅里叶变换后,将加速度在频域下的幅值乘以幅值修正因子2,最终得到各时间段的振动加速度的频域数据。将时间和频率绘制在二维坐标系内,并以色标表示加速度幅值大小,得到如图1所示的振动加速度时频特性云图[5]。轴箱的振动加速度峰值频率随时间历程呈现出增大—保持—减小的趋势,而试验车辆沿时间历程的车速也呈现加速—匀速—减速的趋势,这表明轴箱振动包含随车速变化的车轮转频成分,车辆异常振动现象是由车轮多阶不圆度造成的。

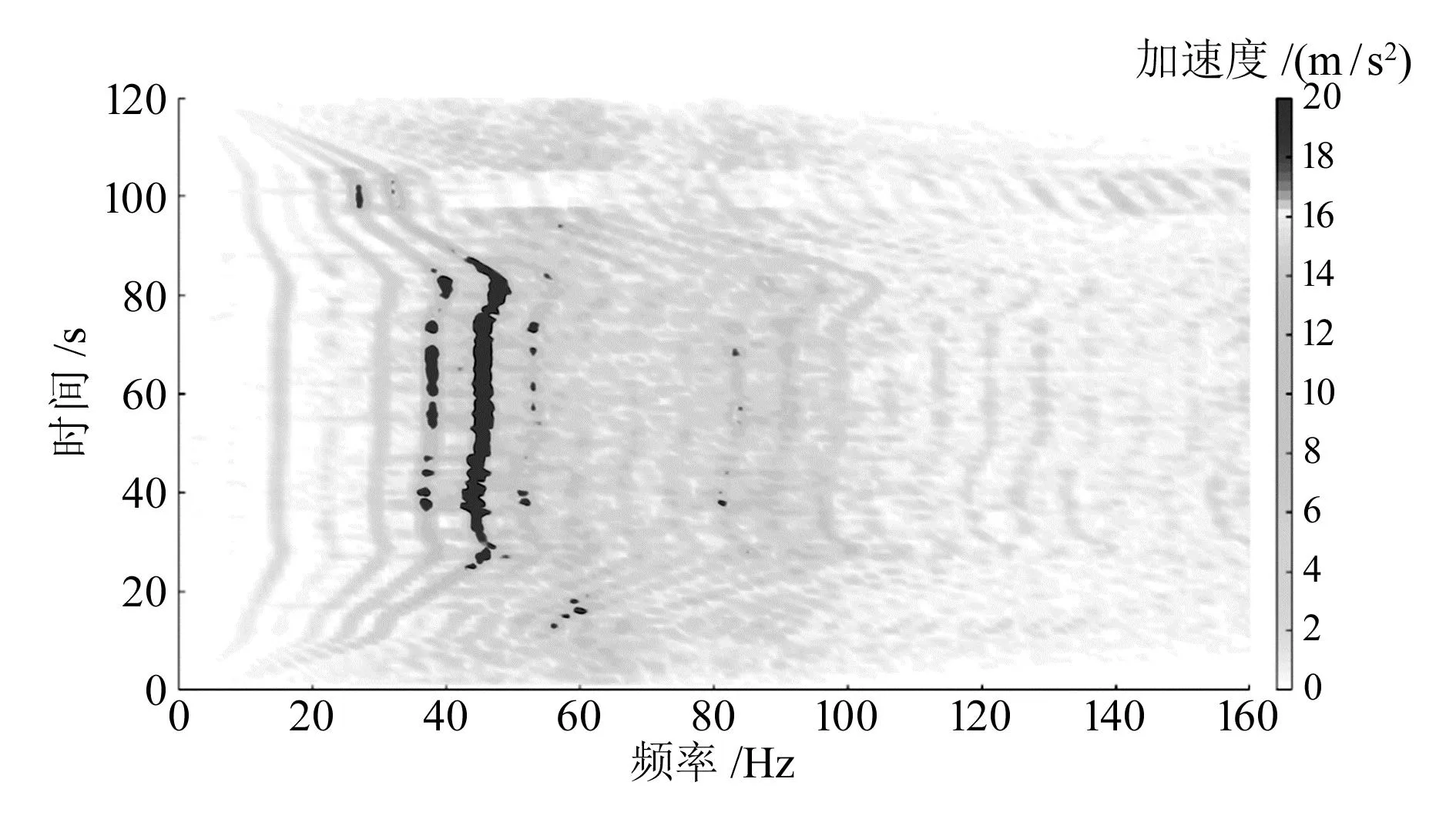
图1 镟修前轴箱振动加速度时频特性

轴箱的振动加速度峰值频率f与车轮不圆度阶次、车辆运行速度和车轮直径有关,其计算公式为[6]:

(1)

式中:v为车速,km/h;n为车轮不圆度阶次;d为车轮直径,mm。

当列车以70 km/h的速度匀速行驶时,轴箱的振动加速度在35、45、52 Hz频率处存在峰值。由式(1)可以计算出这些频率所对应的车轮不圆度阶次为5～7阶(车轮直径为840 mm)。

1.2 车轮不圆度测试及分析

利用车轮粗糙度测试仪对轴箱下方的左右两个车轮进行不圆度测试,传感器测试精度为0.1 μm,采集间距为1 mm(车轮每转过1 mm,测试仪采集一个数据点),测试时车辆需处于制动缓解状态,使用千斤顶同时抬起一个轮对的两个车轮,并保证两个车轮抬升高度一致,传感器与车轮接触位置位于车轮的名义滚动圆处(距轮缘70 mm处),将一磁座吸附于车轮轮缘位置,测试仪磁感装置第一次扫过磁座时,测量开始,第二次扫过磁座时,测量结束,以此记录车轮旋转一周的不圆度数据。

将车轮不圆度数据直观地表示在极坐标下,如图2所示,在车轮不圆度幅值图上,规定测量起始位置的不圆度幅值为0 μm,测量位置的半径大于起始位置时不圆度幅值标为正值,小于起始位置时坐标为负值。由图可以看出,左右两个车轮的车轮径跳均较大,左轮为459.7 μm,右轮为 338.9 μm,并且左轮存在明显的六边形,右轮存在明显的五边形,车轮状况恶劣[7]。

图2 镟修前车轮不圆度幅值图

为更准确地判断车轮不圆度阶次,通过希尔伯特-黄变换,同时参考轮轨接触滤波[8],将车轮不圆度数据换算到波数域上,得到如图3所示的车轮不圆度阶次图,图中纵坐标用对数形式来表示车轮的不圆度幅值,参考值取1 μm。

图3 镟修前车轮不圆度阶次图

由图可以看出左轮和右轮5～7阶不圆度阶次的幅值较大,这与轴箱振动测试结果相符,故针对车轮的不圆度问题,提出了“两刀镟”的控制方案[9],试图通过增大镟修深度消除车轮的5～7阶不圆度现象。

1.3 二次镟修车辆测试分析

对二次镟修后的车辆,进行相同工况下相同轴箱位置处的振动加速度对比测试。对轴箱测点处采集到的振动加速度进行时频特性分析,得到如图4所示的振动加速度时频特性云图,为了方便与镟轮前的振动加速度时频特性云图进行对比,云图的色标采用相同的量程(0～20 m/s2)。结果表明,轴箱的振动加速度在35、45、52 Hz频率处的幅值较镟轮前明显下降。观察图5所示的车轮不圆度阶次图,发现车轮的5～7阶不圆度幅值明显下降,这表明通过对车轮的二次镟修,有效地抑制了车轮的5～7阶不圆度现象,从而抑制了车辆的异常振动现象[10]。

图4 镟修后轴箱振动加速度时频特性

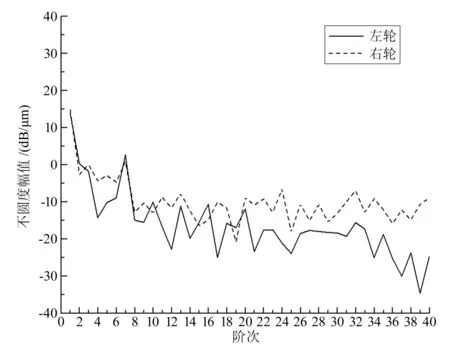
图5 镟修后车轮不圆度阶次图

2 镟修后车辆跟踪测试及对比

为了验证二次镟修控制方案的效果,对二次镟修车辆(记为A车)的车轮进行了车轮不圆度的跟踪测试,并与B车和C车的车轮不圆度数据进行对比。其中B车仅进行了一次镟修,并且在每次进出车库时司机均会采用紧急制动的措施,即每次车辆进出车库时都通过闸瓦磨削车轮踏面来实现对车轮的打磨调整。C车仅进行了一次镟修,不作其他处理。6次跟踪测试车辆运行的里程数见表1。由表可知,第3次试验中A车和C车的镟修后运行里程和第4次试验中B车的镟修后运行里程均达到了45 000 km左右,因此选择第3次试验A车和C车的车轮不圆度数据,以及第4次试验B车的车轮不圆度数据作为对比数据。为了更好地验证“两刀镟”的效果,车轮不圆度的分析对象从所测轴箱下方的左右两个车轮扩展到整节车辆全部的8个轮子。

表1 跟踪测试车辆运行里程表

表2为A、B、C三车车轮径跳数据的统计表,由表可以看出,A车和B车的整体车轮径跳水平相当,范围为50～300 μm,C车整体车轮径跳水平高于A车和B车,范围为100～550 μm,可见每次进出车库时所采用的紧急制动措施有效抑制了车轮径跳发展。

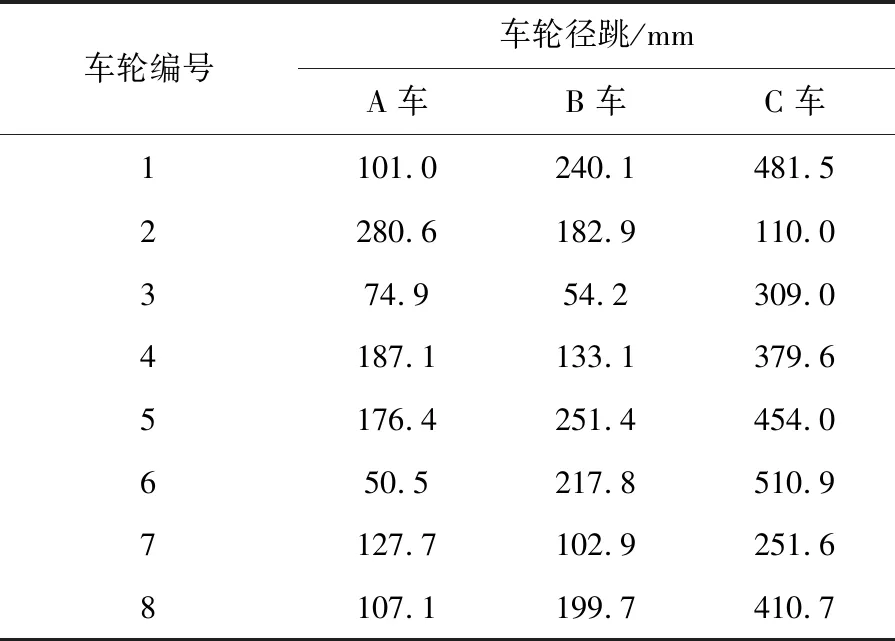
表2 车轮径跳数据统计

根据1.1节和1.2节的分析可知,轴箱在35、45、52 Hz频率处的较高振动能量是由5～7阶车轮不圆度导致的,车辆异常振动现象与5～7阶车轮不圆度有关,图6～图8列出了三车5～7阶车轮不圆度幅值的对比情况,由图可以看出,A车8个车轮5～7阶不圆度的幅值图线整体上位于B车和C车的下方,这也表明A车5～7阶车轮不圆度的幅值整体上小于B车和C车,结合前一章的分析内容可知,A车所采用的“两刀镟”方案可以保证车辆在更长的运行里程中保持较好的运行品质。

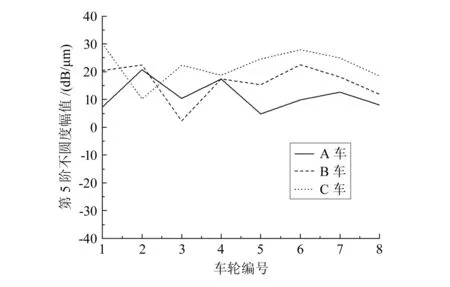
图6 第5阶不圆度幅值对比

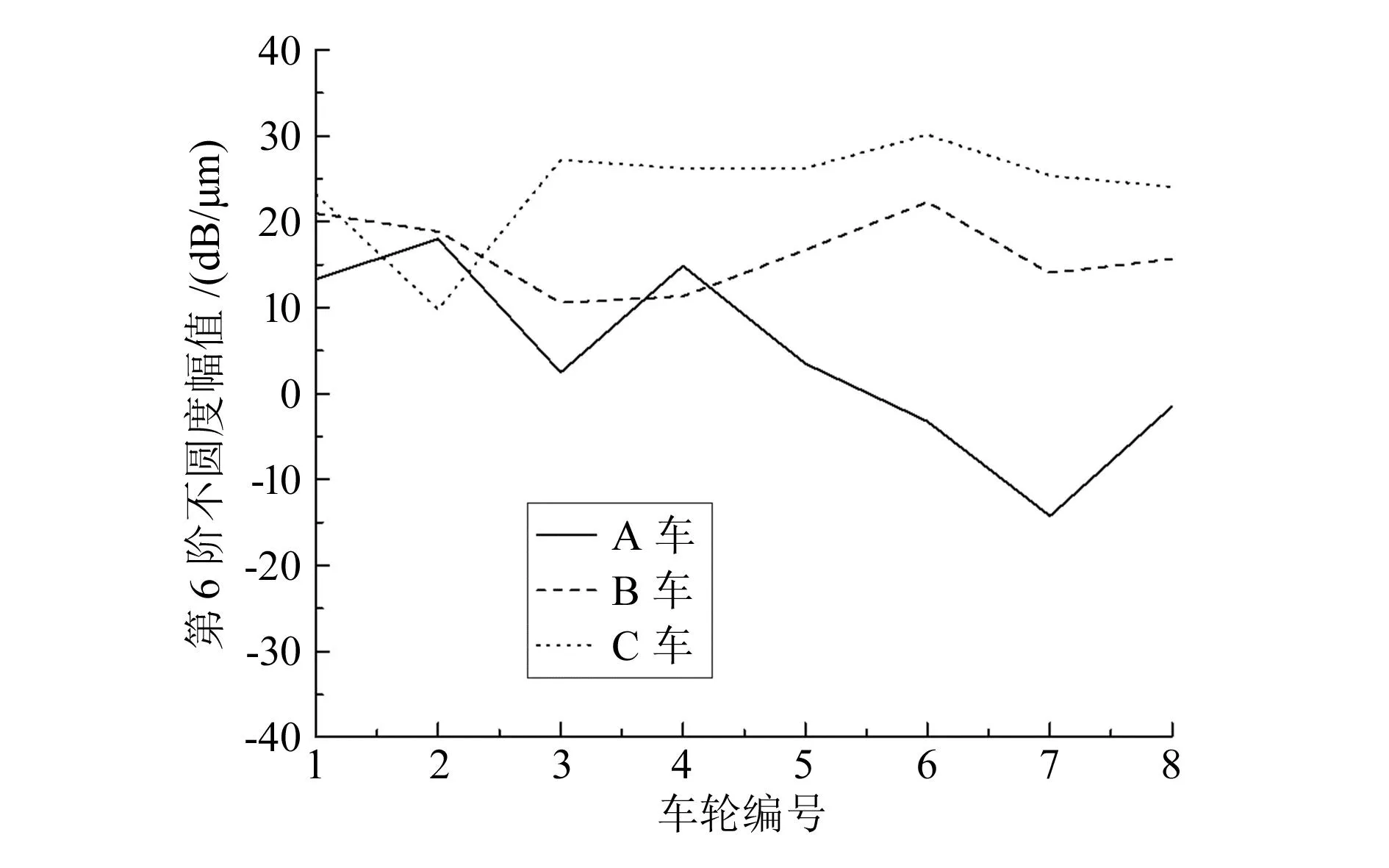
图7 第6阶不圆度幅值对比

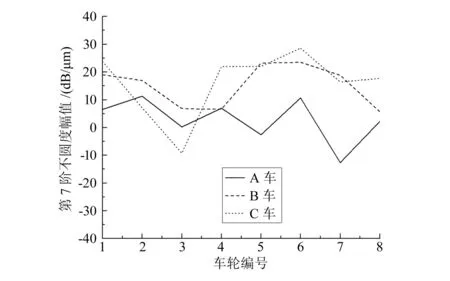
图8 第7阶不圆度幅值对比

综合比较三车车轮径跳水平和5～7阶车轮不圆度幅值的计算结果发现,在进出车库时采用紧急制动措施虽然能抑制车轮径跳的发展,但是无法有效抑制车轮5～7阶不圆度的发展,“两刀镟”方案的控制效果最优。

3 结论

本文探讨了车辆异常振动问题与车轮不圆度现象之间的关系,并有针对性地跟踪研究了不同控制方案的控制效果,研究结果表明:

1)车辆在运行过程中出现的异常振动现象主要是由车轮的第5～7阶车轮不圆度造成的,针对该问题所采用的“两刀镟”的控制方案,在镟轮初期大幅削减了第5～7阶车轮不圆度的幅值,也有效抑制了车辆的异常振动。

2)紧急制动措施在一定程度上可以抑制车轮径跳的发展,但无法有效抑制车轮5～7阶不圆度的发展,而“两刀镟”的控制方案在抑制车轮径跳发展的同时,有效地抑制了车轮5～7阶不圆度的发展,从而保证车辆在更长的运行里程中能保持良好的运行品质。