内波观测浮标水动力性能分析与实验研究

连伟琪,吴俊飞,宋奕萱,曲志平

(青岛科技大学机电工程学院,山东 青岛 266061)

海洋内波是发生在海水内部的一种常见海洋波[1],它对海洋油气工程施工和作业有巨大威胁[2]。我国南海有丰富的油气资源,该海域也是内波频发的海域,通过观测浮标对内波进行观测、预报和预警[3],可以有效避免海洋内波对海洋油气工程的危害。为了确保海洋油气工程施工和作业的安全进行,内波观测数据的有效性和准确性就变得尤为重要。

内波观测浮标是一种浮于水面、搭载多种海洋观测仪器的观测平台,可以连续、定点对海洋内波进行观测。早期的海洋观测浮标为了更加稳定,大多选用大尺寸的浮标[4],如美国的12 m直径的圆盘形浮标和我国使用的直径10 m的HFB-1A型浮标。随着科学技术的发展,为了减少材料成本支出,布放和回收方便,浮标越来越小型化[5]。小型化浮标外形通常为圆柱形、圆盘形、球形等。研究表明[6],圆盘形浮标随波性好、抗倾覆性好,但是横摇响应较大;圆柱形浮标随波性不如圆盘形,但抗倾覆性好、横摇响应小;水下倒圆面结构的浮标随波性好。浮标上装有声学多普勒流速剖面仪(acoustic Doppler current profiler,ADCP)等海流观测仪器,在受到海浪影响时,浮标会发生不稳定的横摇(roll)和纵摇(pitch),当横摇和纵摇的角度值超过20°时,ADCP的观测数据就会失效,由此可知,浮标在进行海洋内波观测时,横摇和纵摇会对观测结果的有效性和准确性产生重要影响。

目前,针对海上浮体的数值模拟研究还处于发展阶段,大多数文章只研究了规律波浪下浮标的水动力特性,对不规律波浪下的浮标模拟研究较少。本文利用AQWA软件,在对浮标进行规律波浪水动力计算的基础上,进一步模拟浮标在不规律波浪下的运动。这样的模拟更接近实际海况,通过海试实验对数值模拟的结果进行验证,不仅能确定所设计浮标的可靠性和模拟的准确性,还能为海洋浮体的数值模拟研究提供参考。

1 浮标结构设计

本文针对75k ADCP,设计了一种小型的稳定性高的内波观测浮标,浮体外形由圆柱形和底部倒圆面组合而成。使用SolidWorks软件进行建模,模型结构如图1所示。浮标主要部件是塔架、浮体、电池舱筒体和ADCP保护架,浮标上的主要仪器有ADCP、定位卫星和通讯装置。通过卫星可以将观测到的数据实时传输到基地,实现内波的实时观测和预警。

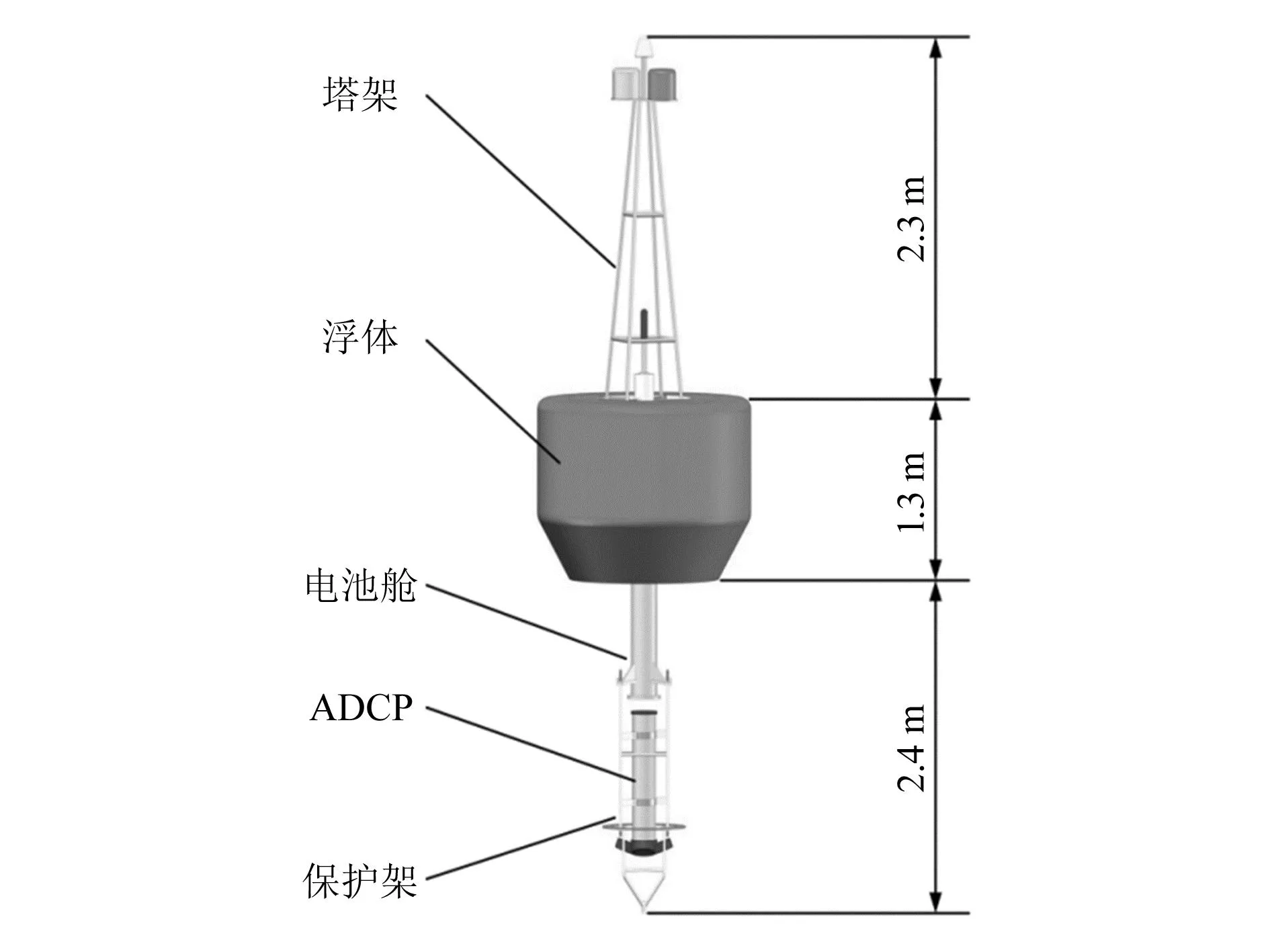
图1 浮标整体结构

整个浮标的高度为6.0 m,其中浮体上方是钢结构的塔架,高度为2.3 m;浮体高度为1.3 m,直径为1.2 m;电池舱筒体的上面部分在浮体内部,电池舱的剩余部分和ADCP仪器保护结构的高度为2.4 m。浮体选用1.5 mm不锈钢板制作,外层起保护作用,内部注充EPS(高密度聚苯乙烯泡沫)作为浮体材料,EPS密度为20 kg/m3,塔架和ADCP保护结构选用316不锈钢。浮标主要部件的质量和可以提供的浮力见表1,其中塔架和ADCP保护架的浮力可以忽略不计,只计算重力。通过表1可以计算出整个浮标的剩余净浮力为4 733.4 N。

表1 浮标主要部件质量和浮力

2 数值模拟

2.1 计算原理

浮体在波浪作用下的运动平衡方程为:

(1)

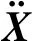
在求浮体结构所受的合外力时,假设流体运动时是无旋的,流体是无黏性、不可压缩的理想流体,就可以用一个速度势φ来描述流场中的速度分布,速度势可以分为3个部分:

φ(x,y,z,t)=φr+φw+φd

(2)

式中:φr为辐射势,φw为入射势,φd为绕射势,x、y、z为坐标,t为时间。

基于三维势流理论,假设浮标在水中受到的压力为p,通过线性化的伯努利方程用速度势来表达:

(3)

通过压力p可以求出浮标在水中受到的合力为:

(4)

式中:S为浮体在水中的表面积,n为浮体指向流场的法向量,Fr为辐射力,Fw为入射波浪作用力,Fd为绕射作用力,Fs为静水力。

不规律波浪通常用波浪谱的方式来模拟,常用的波浪谱为PM谱和JONSWAP谱。PM谱适用于充分成长的海浪,是经验谱,不足以表达复杂海浪情况,其表达式为:

(5)

式中:SPM为PM谱表达式;a为无常数因子,取值0.008 1;g为重力加速度;ω为波浪频率;β为无常数因子,取值0.74;U为离海面10 m处的风速。

本文应用的是JONSWAP谱,其表达式为:

(6)

式中:SJON为JONSWAP谱表达式,A为无因次常数;γ为谱峰升高因子;σ为峰形参数;ωP为谱峰频率。

不规律波浪谱S(ω)作用下的运动响应可以表达为:

SR(ω)=ORA2S(ω)

(7)

(8)

式中:SR(ω)为浮体在波频运动的响应谱;ORA为运动幅值响应算子;mnR为运动方差;n为常数,n∈N。

浮标体的波频运动近似符合瑞利分布,可以求出运动响应的有义值R1/3为:

(9)

2.2 网格划分和参数设置

在浮标的设计与建模过程中,通过SolidWorks软件评估浮标的质量、重心坐标和转动惯量等参数,并计算出浮标吃水线的位置坐标。为了方便模拟计算,用SolidWorks对模型进行简化,如图2(a)所示,导入到AQWA Workbench界面的Hydrodynamic Diffraction模块中进行规律波浪水动力计算,进而在Hydrodynamic Response模块中插入不规律波浪谱和风谱进行频域运动计算。内波观测浮标主要在我国南海北部陆坡区海域进行观测,该海域的海水深度约300 m。因此水域模型设置为边长100 m,水深300 m的正方形海域,海水密度设置为1 025 kg/m3,重力加速度为9.8 m/s2。根据浮标体尺寸设定网格的最大尺寸为0.08 m,自动进行网格划分,得到网格划分模型如图2(b)所示。

图2 浮标简化模型和网格划分

据统计[7],该海域夏季在不受台风影响的情况下,波浪周期出现频率较高的是6～16 s,最大平均谱峰周期7.9 s,平均有效波高1.77 m,最大有效波高为4～5 m,极端天气台风经过时,最大有效波高可达10.66 m。在水动力计算时,波浪周期范围设置为1～20 s,波浪方向在-180°～180°中平均设置8个方向。在进行不规律波浪计算时,分别插入NPD风谱和JONSWAP波浪谱:设置NPD风谱的风速为10 m/s;设置波浪谱的谱峰周期为7.9 s,谱峰因子为1,波浪高度为2、3、4、5 m。

3 结果分析

3.1 水动力计算结果分析

在1.0 m浪高的规律波浪下进行水动力模拟计算,计算结果包括浮体的运动幅值响应算子(RAO)、一阶线性波浪力、附加质量和附加阻尼等。通过计算结果可以分析浮标在不同波浪周期的姿态变化,同时计算结果也为浮标在不规律波浪下的模拟提供了必要数据。

3.1.1RAO

RAO是规律波浪下浮体的运动响应特征,是运动角度和波幅的比值。横摇和纵摇的角度越小,说明浮标体稳定性越好,ADCP仪器的观测效果越好。

横摇和纵摇的计算结果如图3(a)和(b)所示,可以看出,横摇在0°波浪和纵摇在90°波浪的影响很小,其数值几乎为0。在45°和90°波浪影响下,横摇的数值随着波浪周期的增大先急剧变大后迅速变小并趋于稳定,在波浪周期为3 s时,横摇的角度达到最大值,90°波浪方向的横摇角度甚至超过45°,这可能是波浪的周期频率接近简化浮标模型固有频率,产生了共振导致的。由于模型的结构是轴对称的,因此纵摇曲线的变化规律和横摇相似。艏摇是绕浮标中心轴的转动,从图3(c)中可以看出,波浪的周期越大,艏摇的角度越大,在波浪周期为20 s时达到最大值6°,对浮标的影响较小。垂荡是浮标在波浪影响下的垂向运动,从图3(d)中可以看出,随着波浪周期的变化,垂荡在1～2 s周期内快速增大到1.1 m后稳定在1.0 m,说明浮标在1.0 m浪高规律波浪的垂向随波性较好。观测海域的波浪主要能量周期为6～16 s,从图中可以看出,在6～16 s波浪周期内,浮标的横摇和纵摇的RAO幅值均没有超过20°,因此浮标的设计满足仪器有效观测的横摇和纵摇RAO幅值要求。

图3 浮标在规律波浪下的频域RAO

3.1.2一阶线性波浪力

在规律波下的模拟,作用在物体的合力(即一阶线性波浪力)是Froude-Krylov力和绕射作用力的叠加,如图4(a)所示,在高频波浪的影响下,波浪力比较大,在波浪周期为2 s时达到最大值6 kN。随着波浪周期变大,一阶线性波浪力先增大后逐渐减小,最后趋于稳定。浮标横摇的附加质量如图4(b)所示,随着周期增大,附加质量快速增大到峰值后下降并趋于稳定,其受高频波浪影响变化较大。

图4 浮标的一阶线性波浪力和附加质量

3.2 不规律波浪下浮标的姿态变化

由于实际海况的波浪不全是线性规律波,因此需要加入不规律波浪谱和风谱的给定海况进行分析。保持风速方向0°不变的条件下,分别改变波浪方向和波浪高度(2、3、4、5 m)进行模拟计算;模型是对称结构,所以设置了0°、45°、90° 3个波浪方向。给定海况下浮标在3个波浪方向的频域运动有义值见表2、表3和表4。

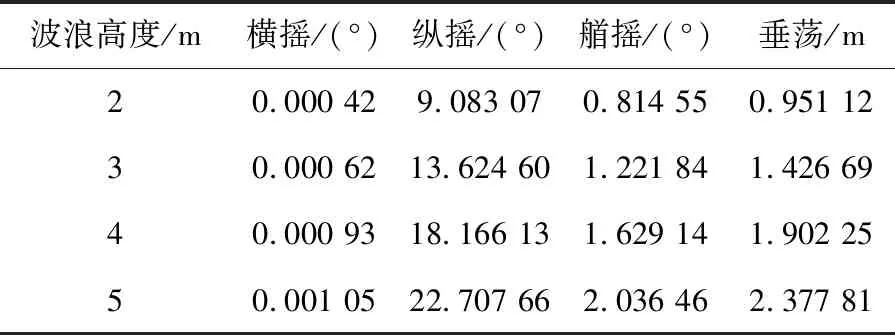
表2 0°波浪方向的浮标频域运动有义值

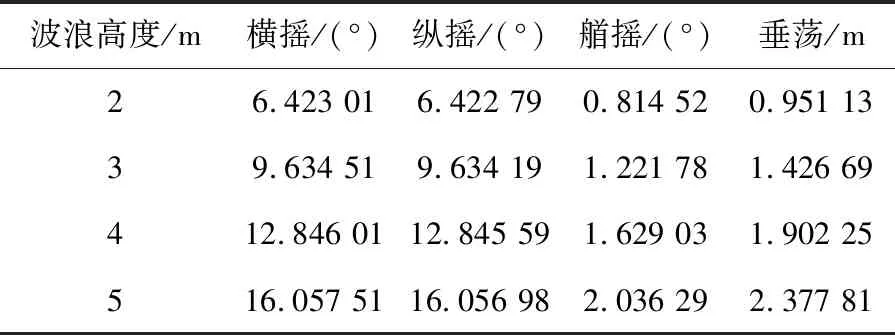
表3 45°波浪方向的浮标频域运动有义值

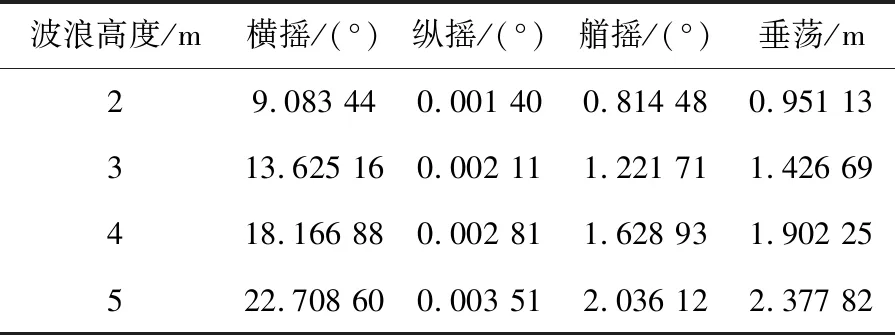
表4 90°波浪方向的浮标频域运动有义值

从表中可以看出,0°波浪方向的纵摇角度最大,90°波浪方向的横摇角度最大;在波浪高度为2～4 m时,不论哪个角度的波浪方向,浮标横摇和纵摇角度的有义值都不会超过20°,符合ADCP仪器有效观测的要求;当波浪高度为5 m时,浮标在0°波浪方向的纵摇和90°方向的横摇角度有义值都增大到22.7°,超过了ADCP仪器有效准确观测的要求角度,所以浮标能够稳定工作、有效观测的额定海浪高度是4 m。浮标的艏摇是绕Z轴(垂直水面方向)的转动,从表中可以看出,波浪方向的变化对艏摇的影响很小,浮标在不同的波浪方向、同一波浪高度的艏摇运动的有义值变化不大,随着波浪高度变高,浮标艏摇角度的有义值逐渐增大,但是艏摇有义值都很小,对仪器观测的准确性影响不大。浮标的垂荡运动也是受波浪高度影响较大,随着波浪高度变高,垂荡运动的有义值也随之增大,在5 m浪高时垂荡达到2 m,但不会对结构的稳定性和仪器观测的有效性造成较大影响。

4 实验验证

为了验证设计的可靠性,浮标于2020年夏季在我国南海北部海域进行布放,图5(a)是在出海过程中对浮标的装配、仪器的安装;图5(b)是浮标成功布放后在海中的姿态,可以看出,在波浪高度不是很大的前提下,浮标十分平稳。

图5 浮标的海试实验

浮标搭载的主要仪器75k ADCP不仅可以对内波的流速方向等要素进行观测,还可监测在海浪影响下的横摇和纵摇值,ADCP固定在浮标下方,如图5(a)中浮标所示。从ADCP中读取了2020年7月27日—2020年8月24日的纵摇和横摇的原始数据,并使用MATLAB软件进行数据处理,绘制出了仪器的横摇和纵摇随时间变化的图像,分别如图6和图7所示。

图6 75k ADCP横摇数据

图7 75k ADCP纵摇数据

由于波浪方向具有不确定性,因此浮标和75k ADCP的横摇和纵摇数值变化比较大。图6中横摇数据正负代表方向不同,绝对值大小代表横摇角度的大小。可以看出,仪器的横摇角度的绝对值大多在0～7.5°,在8月1日和8月22—8月23日横摇角度的绝对值超过了10°,可能是海况较差、海浪较高导致的。在整个时间区间内,最大的横摇角度绝对值也没有超过15°,说明设计的浮标稳定性良好,可以保证75k ADCP持续稳定地进行观测。从图7可以看出,在7月30日—8月3日横摇角度的绝对值较大,在这期间纵摇的角度也较大,可能是海况较差导致的。在其他时间点的横摇角度绝对值大多处于0～5°,说明浮标的稳定性良好。

综合图6和图7可知,在未出现极端天气(如台风)时,浮标整体的横摇和纵摇数据均满足75k ADCP仪器准确、稳定观测的要求,可以保证观测的数据不失效。

5 结论

本文采用AQWA软件分别模拟分析了浮标在规律波浪下和不规律波浪下横摇和纵摇的变化情况,计算得到了不同波浪角度的RAO和频域运动的有义值,并于2020年夏季在南海北部进行了海试试验,得到如下结论:

1) 在规律的波浪下,浮标的横摇和纵摇在观测海域波浪的主要能量周期内都比较稳定,数据较小,均满足75k ADCP仪器的观测要求。在高频波浪的影响下,浮标的横摇和纵摇角度变化较大,在3 s周期的波浪甚至超过40°,这可能是浮标模型的固有频率与波浪频率发生共振导致的。因此在设计浮标时,应考虑实际观测海域的波浪主要能量周期,避免设计的浮标固有频率与波浪频率发生共振。

2) 在给定的海况下进行模拟,当波浪高度在2～4 m时,3个波浪方向的横摇和纵摇统计结果的有义值均没有超过20°,可以保证75k ADCP仪器观测得到的数据准确且不失效。波浪高度为5 m时,在部分波浪方向,浮标横摇或纵摇的角度可能会超过20°,所以从模拟结果看,浮标能够稳定工作、准确观测的额定波浪高度是4 m,波浪高度超过5 m观测到的数据可能会失效。因此,波浪高度是影响浮标稳定的一个重要因素。

3) 浮标在我国南海进行的海试实验验证了模拟的准确性和设计的可靠性。浮标在南海北部海域能够定点、持续、稳定地进行内波观测,观测得到的纵摇和横摇l数值表明,在观测周期内,浮标的横摇和纵摇均满足75k ADCP仪器的观测要求。