基于改进卡尔曼算法的室内温度数据融合

刘陈男，罗 恒，2

(1.苏州科技大学 电子与信息工程学院，江苏 苏州 215000；2.江苏省建筑智慧节能重点实验室，江苏 苏州 215000)

0 引言

近年来，随着人们对室内环境健康和舒适性的关注度不断提高，室内环境数据采集在研究和实践中变得越来越重要，进行室内环境数据采集可以保障人们的健康和安全，提高室内环境的舒适度和节能效率，以及优化室内空间布局和设计，让人们在室内获得更好的使用体验和感受[1]。室内温湿度，光照度，二氧化碳浓度等指标是影响室内环境的关键因素。

对于以时间序列来进行采集的室内环境数据[2]。最常见的是以分钟为单位进行多次采集，采集的密度高种类多，随着时间的推移，越来越多的环境数据会堆叠，数据的复杂程度和数量会大幅提高。数据融合是指将来自不同数据源[3]、不同传感器或不同模态的数据进行整合、分析和处理的过程。在国外，数据融合的研究已经有数十年的历史，主要应用于军事、情报、医疗、环境监测等领域。数据融合技术已经发展出多种方法和算法，例如基于贝叶斯网络的数据融合[4]、基于神经网络的数据融合等[5]。通常的传感器数据融合本质是物理量融合，指对多个传感器测量得到的相同物理量进行融合，如温度、湿度、二氧化碳浓度等。但在实际生活中，一个普通的室内空间有着不止一类传感器，而且同种类传感器的数量也是有限的，以温湿度传感器为例，温湿度的变化过程是比较缓慢的，假设按照固定的采样频率进行采样，会产生冗余数据并且加重了网络传输的负荷，所以传感器的数据融合成为了研究的重点。文献[6]研究了基于卡尔曼滤波算法的温室数据采集系统，通过在温室中放置多个相同种类的传感器监测温度及湿度，对多个同种类的传感器数据进行静态的数据融合，提高了数据采集的准确性。文献[7]设计了在矿井中利用多个同种类传感器对瓦斯数据，一氧化碳浓度，粉尘浓度进行分批估计和自适应加权，对监测数据进行融合。数据融合技术在环境数据处理和分析中具有十分广泛的应用前景。

针对各种数据融合算法的提出，已经在融合精度和复杂度方面取得了一定的提高。然而，这些算法都是在对同一空间的多个传感器的数据进行横向融合的基础上实现的。实际应用中，数据采集是以时间为单位的，采集的密度也很高。因此，将这些数据融合算法应用于基于时间序列的数据融合会带来相对较高的计算复杂性。为了降低数据传输量并提高融合数据的准确性，可以采用纵向融合，即将基于时间序列的数据用卡尔曼滤波算法进行数据融合[8]。然而，传统的卡尔曼数据融合算法存在一个问题，当测量数据出现异常时，可能会导致最终结果出现不同程度的波动。因此，本文的重点研究内容在于如何处理异常值和缺失数据，以进一步提高数据融合算法的准确性和可靠性。对此问题的研究将有助于更好地利用基于时间序列的数据，为各种实际应用提供更好的数据融合解决方案。

1 系统结构及原理

进行室内温度数据采集的系统包括温度数据监测功能和数据处理功能，系统结构如图1所示，系统包含三部分：终端节点，网关节点和云服务器。LoRa终端节点中的STM32主控芯片控制DS18B20温度传感器采集室内实时的温度数据，并通过串口将测量得到的温度数据经由LoRaWAN网络传输到LoRa网关节点，网关节点将其他由终端节点传输过来的温度数据进行汇总，由STM32主控芯片处理后通过4 G模块上传到云服务器进行保存[9]。云服务器上挂载的Python数据处理程序将接收到的数据按照程序内部逻辑进行有规律的储存和分析，最后再进行数据融合。

图1 系统整体结构图

2 系统硬件设计

网关节点和终端节点使用STM32F103RCT6作为主控芯片，并通过SX1278射频芯片进行LoRa网络通信。终端节点由LoRa模块、主控芯片和各种不同类型的传感器构成，这些传感器采集环境数据并将其传输到主控芯片，最后通过LoRa模块进行发送。网关节点的LoRa模块接收到数据后，通过STM32主控芯片将所有传感器数据经由4 G模块发送到云服务器。通过这种方式，环境数据可以在云端进行进一步处理和分析，例如生成报告和制定决策等。在这个系统中，LoRa网络通信技术被广泛应用，其具有较远的传输距离、较低的功耗和高度的可靠性等优点，能够满足室内环境数据采集和传输的要求。同时，STM32F103RCT6主控芯片具有高性能、低功耗和丰富的外设接口等特点，为该系统的高效运行提供了保障。

2.1 主控芯片

主控芯片STM32F103RCT6是由ST公司开发，基于ARM Cortex-M3内核，可以采用I2C，SPI，UART/USART等通信协议和外设模块进行数据传输。其内置了48 K的RAM，256 K的FLASH，包括电源电路，晶振电路和复位电路，最高主频可达72 MHz，满足绝大部分的使用场景。

2.2 LoRa模块

LoRa是一种基于扩频技术的低功耗、长距离、低速率的无线通信技术，它是低功耗广域网(LPWAN)中的一种。使用频率偏移调制(FSK)或扩频技术在无线电频段发送数据包[10]。与其他低功耗无线通信技术相比，它具有更长的通信范围和更长的电池寿命。它可以在数公里范围内传输数据，同时保持非常低的功耗，这使得LoRa非常适合需要低速、低功耗和长距离通信的应用，如智能城市、智能家居、物联网等。本系统使用SX1278射频芯片通过SPI协议与STM32进行数据传输。LoRa模块的电路原理图如图2所示。

图2 LoRa模块电路原理图

2.3 温度采集模块

温度采集模块选取的是DS18B20传感器，由于它采用的是单线通信协议[11]，所以只需要一条数据线就可以实现数据的传输和控制，并且输出数字信号，便于数字化系统处理和数据传输。测量范围在-55 ℃到+125 ℃，精度可以达到±0.5 ℃。DS18B20模块的电路原理图如图3所示。

图3 DS18B20模块电路原理图

3 系统软件设计

为了避免在终端节点与网关节点进行通信时出现主动发送数据、信道抢占和互相干扰的情况，导致数据传输过程中出现差错，采用了一种基于星型拓扑结构构造的LoRa组网结构。在该结构中，整个LoRa网络中的各终端节点通过点对点的方式连接到一个中央节点，即LoRa网关。这种构造方式可以避免终端节点之间的干扰，保证数据传输的稳定性。同时，终端节点和网关节点之间的交互方式采用了轮询方式，使得通信过程更加高效和可靠。

3.1 终端节点软件

在LoRa终端节点首次上电后，STM32主控芯片会对串口进行使能以及SPI接口进行初始化。通过使用C语言编程开发，并借助Keil5软件，对STM32主程序进行开发。通过SPI接口发送AT指令对各节点的LoRa模块进行初始化并配置不同的地址和信道。这样可以在网关节点上区分不同传感器设备上传的环境数据，同时也减少了传输过程中可能出现的错误数据。在主控芯片程序中，还定义了一些自定义函数用于传感器的初始化，并在收到网关节点发出的唤醒指令后，采集实时的环境数据。该数据随后通过USART串口发送到主控芯片，主控芯片接收到数据后再将其按照固定的格式封装成数据帧，并发送到网关节点[12]。LoRa终端节点的软件流程图如图4所示。

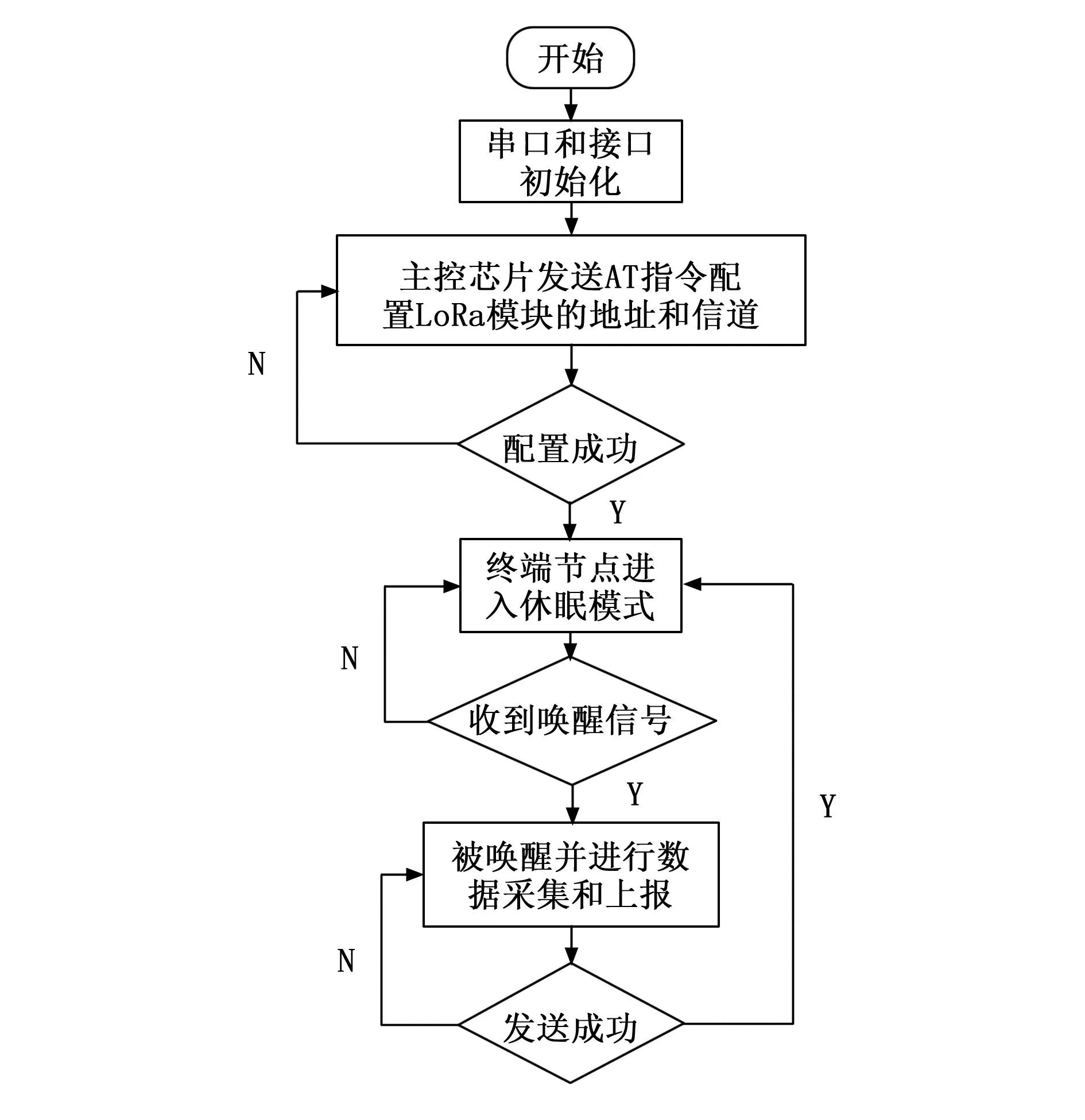
图4 终端节点软件流程图

3.2 网关节点软件

在网关节点首次上电后，STM32主控芯片对4 G模块发送AT指令进行初始化配置，其中包括设置4 G模块的传输模式和服务器的地址端口号等，同样，需要对LoRa通信模块配置地址和信道。STM32主控芯片的程序流程为将唤醒指令通过LoRa网关依次发给终端节点，再接收LoRa终端上传的传感器数据，接收完成后在主程序中进行数据帧格式的判断，保证数据的正确性和完整性。确认数据无误后，将接收到的数据通过4 G模块发送给服务器进行进一步的数据预处理和算法过滤。LoRa网关节点的软件流程图如图5所示。

图5 网关节点软件流程图

4 融合算法

4.1 卡尔曼滤波算法

卡尔曼滤波算法是一种高效率的递归滤波器，其主要应用于估计动态系统的状态，尤其是从一系列包含噪声的测量中。该算法采用信号与噪声的状态空间模型[13]，通过利用前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计，从而计算出当前时刻的估计值。由于其精度高、效率高和可靠性强等特点，卡尔曼滤波算法已经广泛应用于诸多领域，包括航空航天、自动控制、信号处理等。其本质是由量测值来重构系统的状态向量，以“预测—实测—修正”的顺序递归来消除随机干扰[14]，逐步实现达到最优估计的效果。

一般形式下的卡尔曼状态空间方程为：

状态方程：

Xt=AXt-1+BUt+Wt

(1)

观测方程：

Yt=HXt+Vt

(2)

在上述的状态方程和观测方程中，Xt为t时刻的系统状态，Xt-1为上一时刻的系统状态，Ut为系统在t时刻的输入信号，Wt为系统在t时刻的过程噪声，Vt为t时刻的观测噪声，A为状态转移矩阵，B为控制矩阵，H为观测矩阵。由卡尔曼的状态方程和t-1时刻的最优估计值可得出t时刻的预测值，也就是先验估计为：

(3)

对应的先验估计协方差为：

(4)

式中，Q的对应的过程噪声Wt的方差，为了得到当前t时刻的最优估计值Xt，需要结合公式(2)和(3)得出t时刻的最优估计值，也就是后验估计值Xt，其公式为：

(5)

在计算出t时刻的最优估计值后，需要对卡尔曼算法进行迭代运算，要更新上式中的卡尔曼增益Kt和Xt所对应的后验估计协方差Pt，卡尔曼增益Kt和后验估计协方差Pt的公式如下：

(6)

(7)

式中，R为观测噪声Vt的方差，I为单位矩阵。

4.2 卡尔曼滤波的参数设置

在实际的应用中，需要根据测量数据的实际情况进行参数的设置。该算法的应用场景是建筑物内部的某个有流通性的空间，并不是一个密闭空间，所以会与外界的空间存在热量交换导致的过程噪声[15]，室内的环境属于一维系统，将一般的卡尔曼滤波方程改造成一维状态下的卡尔曼滤波方程，其中A=H=1，由于整个系统没有控制量，Ut=0，过程噪声Wt和观测噪声Vt对应的方差分别是Q和R，R由测量仪器的精度决定，Q一般设置为一个确定的值，取值越接近0，融合的曲线越光滑。初值X0可以取0或者初始的测量值。在一般情况下，初始协方差P0的值越小代表初始的估计较好。

4.3 改进的卡尔曼滤波算法

4.3.1 孤立森林算法

在一个相对稳定的数据采集环境中，传统的卡尔曼滤波算法可以获得一个较为理想的数据融合结果。然而，由于周围环境的突然改变或传感器本身的机械故障等原因，异常值或缺失值可能会出现，导致传统的卡尔曼滤波算法出现不同程度的波动。为了解决此类问题，引入孤立森林算法对原始数据进行预处理[16]，再利用卡尔曼数据融合算法进行融合，从而得到更加准确的融合结果。孤立森林算法是一种基于Ensemble的快速离群点检测方法，具有线性时间复杂度和高精度。该算法不依赖于距离、密度等量化指标来比较样本之间的差异。它使用孤立树iTree[17]，这是一种结构为二叉搜索树的孤立树，用于孤立样本。由于异常值数量较少，样本疏离度高等特征，异常值可以在样本中被早期孤立出来。因此，通过使用孤立森林算法预处理数据，可以更好地提高卡尔曼数据融合算法的融合效果，从而获得更加准确的融合结果。

该算法的大致流程可以分为两个步骤，第一步是构建出孤立树组成孤立森林，具体过程如下：

对需要被测量的对象进行多次测量，得到的数据集可表示为：

X={x1，x2，x3，…，xn}

(8)

从X数据集中随机选择ψ个样本点并将其作为数据集X的子集X′放入根节点后，需要在数据集的m个维度中随机选择一个维度q，在当前数据集中随机选择一个切割点p，以便满足以下条件：

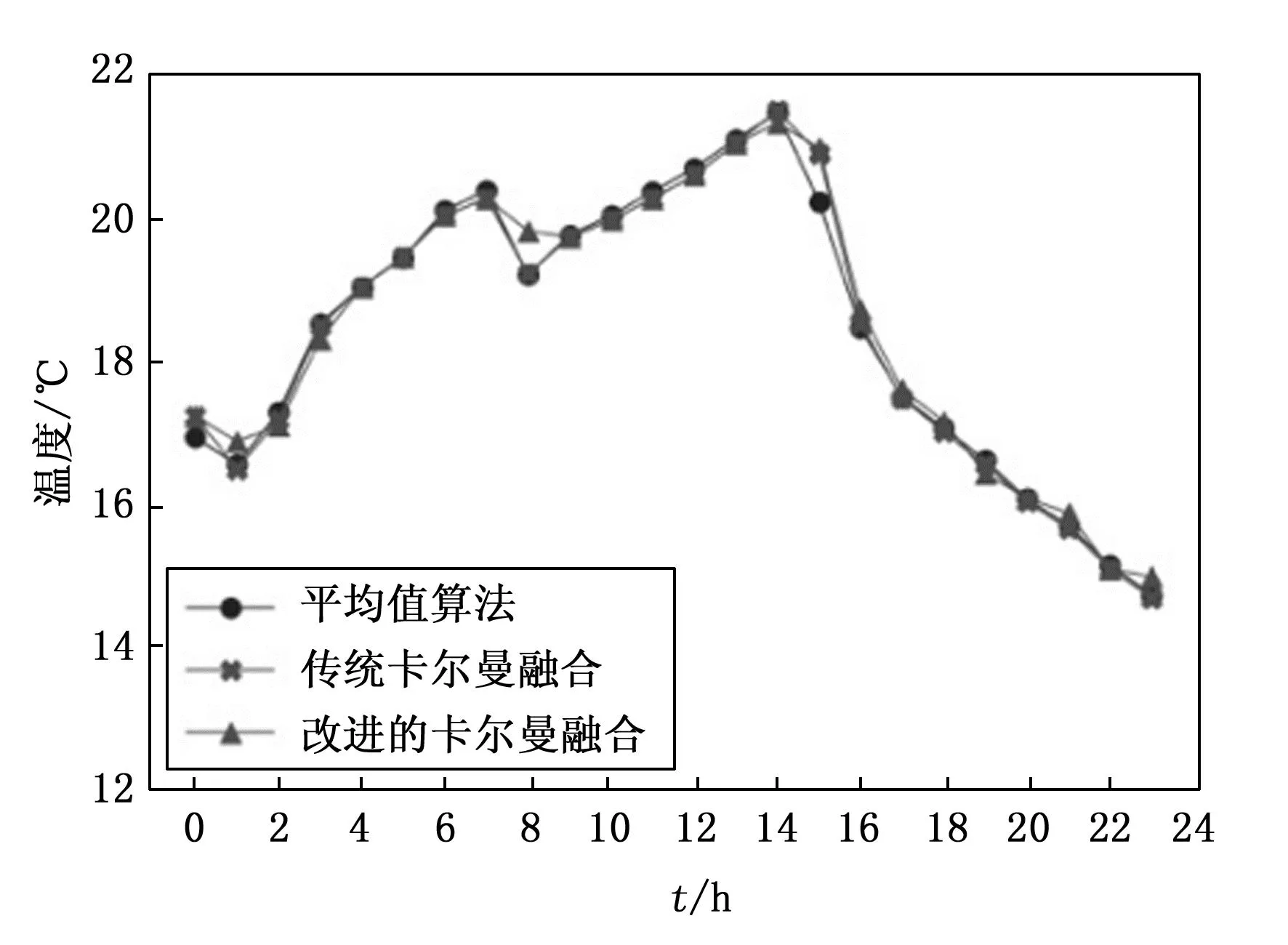
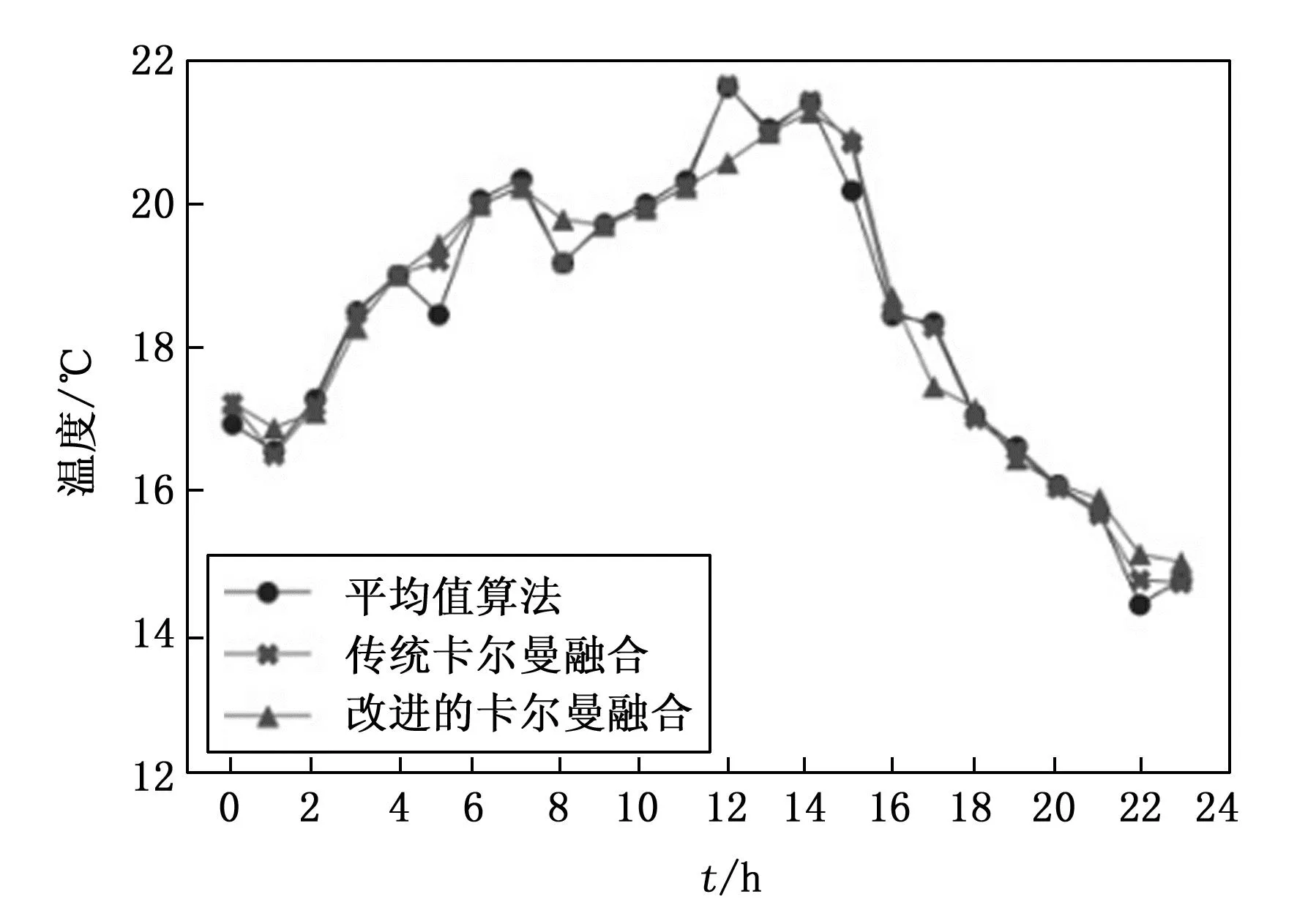
Min(xij，j=q)

(9)

以随机选择的切割点p生成一个超平面。该超平面将数据空间划分成为两个子空间，其中小于p的样本点被指定为左子节点，大于或等于p的样本点被指定为右子节点。然后，递归地随机选择一个维度和一个点p，并重复上述操作，直到所有叶子节点都只有一个数据或达到了预设的iTree高度。最后，上述操作会循环执行，直到生成T个iTree。然后使用这些iTree来预测数据的异常分数，并据此识别异常值。

第二步是将每个样本点带入孤立森林中的每棵孤立树，以此来计算每个样本点的异常值分数和平均高度。其具体过程如下：

在获得T个iTree后，对每一个数据xi，让这个数据遍历每一棵iTree，从而计算xi在森林中的平均高度h(xi)，对所有的数据点的平均高度做归一化处理。异常值分数的计算公式如下所示：

s(x，ψ)=2E(h(x))/c(ψ)

(10)

s(x，ψ)代表记录数据xi在ψ个样本中的训练数据构成的iTree的异常指数，其中：

(11)

H(k)=lnk+ζ，ζ=0.5772156649

(12)

当异常值被识别出，为了保证数据质量和完整性，提高数据的可用性，避免误导性分析，可以通过对异常点周围数据取平均值来替代异常点数据来保证数据的完整性。

4.3.2 融合算法步骤

改进的卡尔曼数据融合算法步骤如下：

1)将原始的室内温度数据导入孤立森林算法中，利用孤立森林算法识别异常数据，并用平均值算法代替原始数据中的异常数据。

2)确定卡尔曼滤波算法的参数，设置状态转移矩阵A，控制矩阵B，观测矩阵H的值和X0，P0的初始值。

3)使用卡尔曼滤波算法对采样数据进行迭代运算，得到数据融合的结果。

5 实验结果与分析

选取南方2月份一个学校内的教室进行为期一天的室内温度数据采集，每隔三分钟进行一次采样，一小时会得到20个室内温度数据，24小时可以得到480个采样数据，分别使用平均值法，传统的卡尔曼数据融合算法和改进的卡尔曼数据融合算法按小时对480个室内温度数据进行融合，融合成为24个数据。

5.1 原始采样数据的融合

使用平均值法[18]、传统的卡尔曼数据融合算法以及改进的卡尔曼数据融合算法对采样数据进行了融合。如图6所示，融合结果反映了一天内室内气温的变化趋势。在下午2点到3点期间，室内温度达到最高点。3种方法在融合趋势方面大致相同，但都存在微小的突变。然而，与平均值算法和传统的卡尔曼数据融合算法相比，改进的卡尔曼数据融合算法的突变程度更低，更加符合室内温度缓慢变化的客观规律。这表明改进的算法在数据融合方面具有更好的性能，能够更准确地反映室内气温的变化。

图6 3种方法的原始数据融合曲线

5.2 添加扰动样本和畸变数据

为了验证改进的卡尔曼数据融合算法的性能，在原始的室内温度采集数据中添加了扰动样本和畸变数据[19-21]。扰动样本是指对原始数据进行随机增加或减少的操作，以模拟真实世界中可能出现的干扰情况。而畸变数据则是通过将原始数据设置为最大或最小值，来产生异常数据。这些异常数据的具体设置如表1所示，旨在考察算法在面对不同程度的干扰和异常数据时的鲁棒性和性能表现。通过这些实验，能更全面地评估改进的卡尔曼数据融合算法的性能。

表1 设置的异常数据

将设置的8个异常数据替换原始数据，将带有异常值的480个数据带入孤立森林算法进行判别，异常数据均被识别成功并赋予了新的值，并且估计值与原始数据的误差控制在-0.47～0.44，如表2所示。

表2 异常数据的估计值

对添加了扰动样本和畸变数据的采样数据分别采用平均值法、传统的卡尔曼滤波算法和改进的卡尔曼滤波算法进行融合结果的比较，带有扰动样本的融合结果对比如图7所示，同时对3种方法的融合误差也进行比较，如表3所示。带有畸变数据的融合结果对比如图8所示，3种方法的融合误差如表4所示。

表3 3种融合方法带有扰动样本的误差

表4 3种融合方法带有畸变数据的误差

图7 3种方法带有扰动样本的融合曲线

图8 3种方法带有畸变数据的融合曲线

由图7和表3可得，在4个时间点设置的扰动样本，平均值法均有较大程度的波动，平均值法的误差在-0.6～0.29的大范围变化，传统的卡尔曼数据融合算法在-0.17～0.56之间波动，相较于平均值法，波动范围已经缩小，而改进的卡尔曼数据融合算法波动范围控制在-0.12～0.1之间，基本上不受扰动样本的干扰。

通过观察图8和表4可以得出，畸变数据对数据融合结果的影响远大于扰动样本的影响。在12点和17点，平均值法和传统的卡尔曼数据融合算法都出现了较大程度的变化。然而，通过改进后的卡尔曼滤波算法处理畸变数据，由于孤立森林算法能够准确地识别和替换畸变数据，融合误差范围在-0.03至0.14之间。相比之下，平均值法的误差范围在-0.99至0.95之间，传统的卡尔曼滤波算法的误差范围在-1.11至0.36之间。

综合以上实验结果，可以得出改进的卡尔曼数据融合算法在处理类似于扰动样本和畸变数据等异常数据时，不会出现融合值的突变，能够获得较为平滑的融合效果，融合曲线也更加平缓。因此，改进后的卡尔曼数据融合算法具有较强的鲁棒性，能够更加稳定和可靠的处理异常数据。

6 结束语

本研究采用了LoRa无线通信模块和传感器组成了室内环境数据采集系统来监测室内温度数据的变化。由于室内温度数据变化缓慢，并且是在同一空间下的基于时间序列的数据，所以提出了一种应用在一维线性空间中的改进的卡尔曼滤波算法。经过实验验证，该算法可以规避扰动样本和畸变数据带来的影响，提高了融合算法的鲁棒性，能够更加准确的掌握室内温度的变化。