调谐质量阻尼器和非线性能量阱抑制内燃机闭环轴系扭转振动的比较研究1)

马 凯 杜敬涛,2) 刘 杨 陈曦明

* (哈尔滨工程大学动力与能源工程学院振动噪声控制研究所,哈尔滨 150001)

† (中国运载火箭技术研究院北京航天发射技术研究所,北京 100076)

引言

内燃机轴系的扭转振动作为发动机运动系中最常见的振动,是衡量动力装置是否安全运行的重要指标之一[1].轴系扭转振动的恶化会使其在运行时产生附加的扭转交变应力,冲击发动机附件系统,磨损齿轮机构,从而影响整个发动机的NVH、燃油经济性和可靠性[2].因此,合理控制内燃机的扭转振动至关重要.

要对内燃机轴系扭转振动问题进行合理的减振研究,首先应考虑影响轴系扭转振动的外界复杂非线性激励.近年来,许多学者已对影响内燃机轴系扭转振动的非线性因素展开了研究.在文献[3-6]中,研究者们将发动机曲轴视为开环模型,考虑了缸内燃烧对曲轴扭振的影响规律.Wang 等[7]假设发动机润滑良好,建立了行星齿轮混合动力系统扭振模型,研究了行星齿轮啮合刚度对轴系扭转振动的变化规律.此外,Mitm 等[8]对混合动力汽车动力系统的扭振非线性动力学行为进行了研究,结果表明,当系统参数发生变化时,产生了包括混沌在内的一系列重要现象.同时,Ni 等[9]提出了发动机喷油提前角耦合曲轴扭转振动模型,研究喷油提前角对曲轴扭转振动的影响规律.Guo 等[10]为了稳定发动机转速,提出了考虑转速反馈的PID 闭环控制模型,显著提高了曲轴转速的稳定性.Vollberg 等[11]针对曲轴系统提出了一种闭环控制策略,并实时提取转矩和转速信息,得到了准确的控制结果.Ma 等[12]在前人研究的基础上,提出了闭环曲轴的概念,即,在建立曲轴数学模型时,考虑曲轴的转速和扭转位移波动,并实时反馈给外激励.外激励、曲轴和输出响应构成一个完整的非线性闭环自激耦合振荡(nonlinear closed-loop self-excited coupled oscillation,NCSCO)模型.显然,与传统的开环模型相比,闭环曲轴模型能更好地反映发动机的真实运行状态.

在工程扭振减振领域,经过多年的探索,研究者们提出了各种缓解内燃机轴系扭转振动的吸振器.例如,调谐质量阻尼器[13]、双质量飞轮减振器[14-16]和离心摆式减振器[17-19]等,上述吸振器虽然有效地抑制了扭转振动,但仅局限在较窄的减振频带范围内.为此,Vakakis 等[20]首次提出了非线性能量阱(NES)的概念,通过使用NES,改善了常规线性减振器的吸振效果,拓宽了吸振频带.NES 与主体结构之间能量传递的机制被称为靶向能量传递(targeted energy transfer,TET).NES 作为一种新型被动控制技术,近年来被广泛应用于梁结构[21-22]、板壳结构[23-24]以及旋转轴[25-27]的减振控制领域,并取得了良好的减振效果.除此之外,Ahmadabadi 等[28]针对单缸发动机曲轴,使用复化平均法分析了NES 实现TET 的关键临界条件.Haris 等[29-30]则对带有NES 的发动机推进轴系进行了大量的数值仿真计算,结果表明,NES 在推进轴系中的减振效果本质上是通过TET和模态间能量传递实现的.上述文献已经证实了调谐质量阻尼器(TMD)和NES 在扭转振动领域的吸振机理,但定量考虑闭环曲轴扭振的TMD 和NES减振对比的研究仍有待探索.

基于此,本文将以一台多缸船用型柴油机为研究对象,建立考虑包括缸内燃烧压力和惯性力等外激励在内的M-NCSCO 模型,并通过实验验证MNCSCO 模型的正确性.在此基础上,对该模型分别耦合TMD 和NES,并使用改进的Newmark-β积分方法对该强非线性常微分方程组进行数值求解,定量对比分析TMD 和NES 在不同的设计参数下对内燃机轴系扭转振动的影响,为未来NES 在曲轴扭振减振中的应用提供参考依据.

1 模型建立与验证

1.1 曲轴扭转振动模型的建立

基于集总参数法简化原则[31],在保证系统简化前后动能、势能等动力学参数保持不变的前提下,将图1 所示的4190 型柴油机轴系系统简化为由 10个仅有转动惯量而无弹性形变的集中惯量 (J1～J10)和9 个仅有弹性形变而无转动惯量的轴段 (K1～K9) 所组成的集总参数模型,所简化的轴系当量系统如图2 所示.J1～J10分别为皮带轮、齿轮系、气缸1、气缸2、气缸3、气缸4、飞轮端齿轮系、飞轮、联轴器和测功机转动部件的简化转动惯量.

图1 4190 柴油机示意图Fig.1 4190 diesel engine diagram

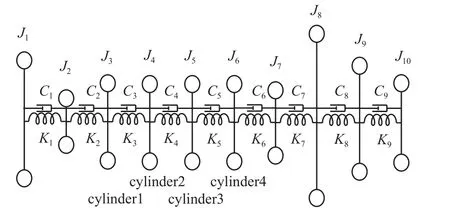
图2 某四冲程柴油机轴系集总参数模型Fig.2 Lumped parameter model of a four-stroke diesel engine shafting

此时,系统的动力学微分方程为

其中,K,M和C分别为系统的刚度、质量和阻尼矩阵.其刚度、转动惯量和阻尼的值由文献[32]给出,T为系统的广义外激励向量,表达式见下

式中,Tc3,Tc4,Tc5,Tc6分别表示4 个气缸曲拐位置受到的扭转力矩,此处的省略部分为0.Tl为测功机扭矩,假设为常数.

式中,θ1～θ10为J1～J10相对应的扭转位移.

1.2 M-NCSCO 模型的建立

曲轴受到来自缸内复杂交变力的作用,这是内燃机轴系扭转振动的根本来源.以单一气缸为例,介绍缸内燃烧压力和惯性力转化为曲轴扭转力矩的过程.如图3 所示,Fi是燃烧室内的燃烧压力,Fe为活塞和连杆运动产生的惯性力.Fi和Fe可通过曲柄连杆机构转化为Ti和Te,它们作为燃烧力矩和惯性力矩作用在曲轴曲柄上.其中,Ti为主动力矩,Te为阻力力矩.β为连杆摆角,θ为曲轴转角.

图3 单一气缸非线性外激励示意图Fig.3 Single cylinder nonlinear external excitation diagram

总的扭转力矩Tc考虑了燃烧力矩Ti和惯性力矩Te,如下所示

式中,Ti是燃烧力矩,它由燃烧压力p,缸径d以及传递函数f1决定,如下所示

式中,r是曲柄半径,l是连杆长度.惯性力矩Te的表达式见下式

式中,mj是活塞环、活塞、活塞销和连杆小端质量的总和.

由式(7)～式(11)可以看出,各部分外激励是随曲轴转角θ及转速dθ/dt不断变化的函数.如图4 所示,燃烧力矩Ti、惯性力矩Te和外界负载Tl构成了曲轴的输入,曲轴角位移和角速度构成了曲轴的输出.其中,Ti受到角位移反馈,Te同时受到角速度和角位移反馈.外激励、系统和输出角速度及角位移构成了闭环回路,显然,这是一个非线性自治系统.

图4 闭环轴系回路示意图Fig.4 Diagram of closed loop shafting circuit

1.3 实验验证

为了验证所建立模型的正确性,通过如下实验步骤进行实验验证.首先,测量4190 柴油机气缸压力曲线,设计试验柴油机运行参数如表1 所示.设计的试验工况为50%～100%负荷工况,即110～220 kW.转速为1000 r/min,喷射正时为−26°ATDC (after topdead center).这意味着喷油过程在活塞上止点前26°完成.气缸压力信号由气缸压力传感器采集,采样步长设为0.2°.

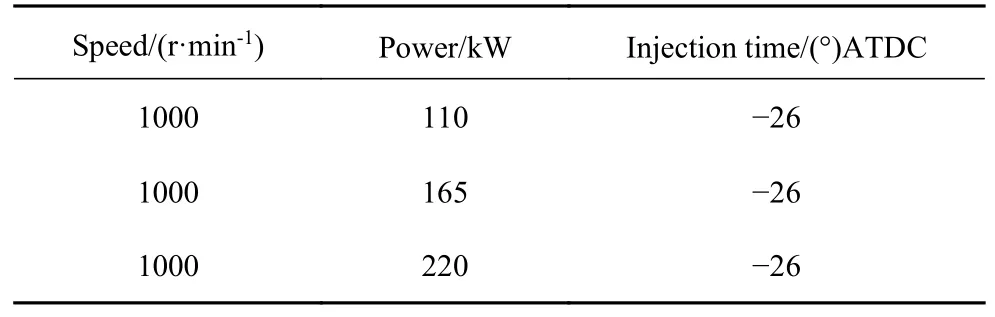
表1 发动机运转时的主要状态Table 1 The main parameters of marine diesel engine operating conditions

图5 展示了柴油机在1000 r/min,喷油提前角为−26°ATDC 条件下,施加50%,75%和100%负荷时所测得的缸压曲线.将3 种工况下的缸压曲线输入到所建立的M-NCSCO 模型中,通过对模型测功机位置施加反向力矩调整模型输出转速稳定在1000 r/min,可以得到3 种功率下的扭矩分别为980,1530 和2090 N·m.而实验工况下测得的扭矩分别为1050,1575 和2100 N·m.将实验值和仿真值的对比可以发现:110 kW 状态下,模型误差最大,为6.7%.220 kW 条件下,模型误差最小,为0.5%.为了使结果更具说服力,接下来将使柴油机运行在1000 r/min,220 kW,100%负荷条件下进行仿真.

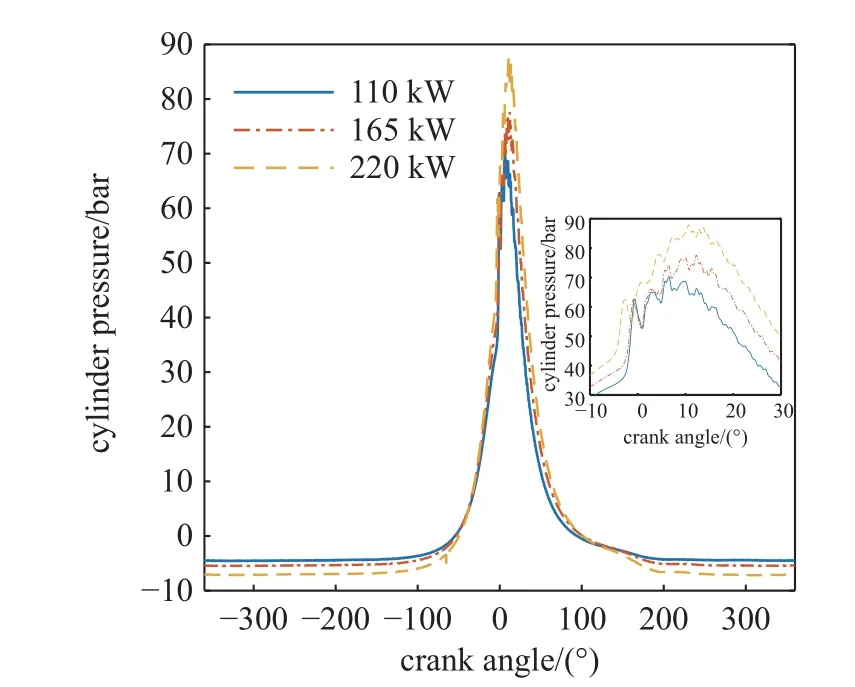
图5 单一气缸内燃烧压力随曲轴转角的变化曲线Fig.5 The curve of the combustion pressure in a single cylinder with the angle of the crankshaft

2 M-NCSCO 模型耦合DVA

2.1 耦合TMD 模型的建立

本小结对该轴系耦合TMD,其动力学模型如图6所示.

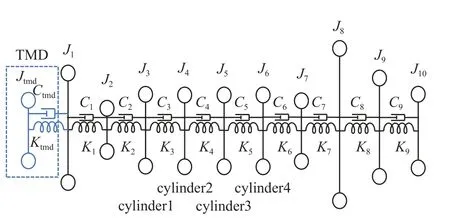
图6 附加TMD 的四冲程柴油机轴系集总参数模型Fig.6 Lumped parameter model of four-stroke diesel engine shafting coupled with TMD

此时,耦合TMD 系统的动力学微分方程为

式中,Kl,Ml和Cl分别为附加TMD 后系统的刚度、质量和阻尼矩阵,Tl为附加TMD 后系统的广义外激励向量,表达式见下

其中

式中,θl为TMD 的扭转角位移.

2.2 耦合NES 模型的建立

对该柴油机轴系耦合NES 后的动力学模型如图7 所示.

图7 附加NES 的四冲程柴油机轴系集总参数模型Fig.7 Lumped parameter model of four-stroke diesel engine shafting coupled with NES

需要注意的是,式(20)是根据Newmark-β法的计算规则[33]建立的等效微分方程.其中,Kn,Mn和Cn分别为附加NES 后系统的等效刚度、等效质量和等效阻尼矩阵.Tn为附加NES 后系统的等效广义外激励向量.式中,系统耦合NES 后产生的非线性刚度项被转移到了Tn中,它们的表达式如下

此时,系统的动力学微分方程为

其中

其中,−Knes(θ1−θn)3为非线性弹簧刚度产生的弹性力,省略号部分元素为0.

式中,θn为NES 的扭转角位移.

3 数值仿真分析

在本节中,将利用前文所测得的220 kW 下的缸压曲线作为输入,考虑DVA 设计刚度、阻尼及位置布置对曲轴扭转振动的影响,讨论TMD 和NES 在以上3 种状态下的性能优劣.为了避免得到局部最优解,阻尼取值的范围为0.202～20 200 N·m·s/rad,刚度取值的范围为2.6×101～2.6×1013N·m/rad (N·m/rad3).

如图8 所示,以某一仿真工况下J1和J2之间的轴段扭转振动为例:相邻轴段之间的扭转振动由瞬态过程和稳态过程组成.从图中可以发现,NES 和TMD 在瞬态和稳态过程中的减振性能略有不同.为了衡量DVA 对曲轴扭振减振的影响,定义振动烈度函数(vibration intensity,VI)[27].如下式所示,该振动烈度函数综合考虑了曲轴9 个轴段在瞬态及稳态仿真时间内的均方根值和振动最大值.VI的值越小代表DVA 的减振性能越强

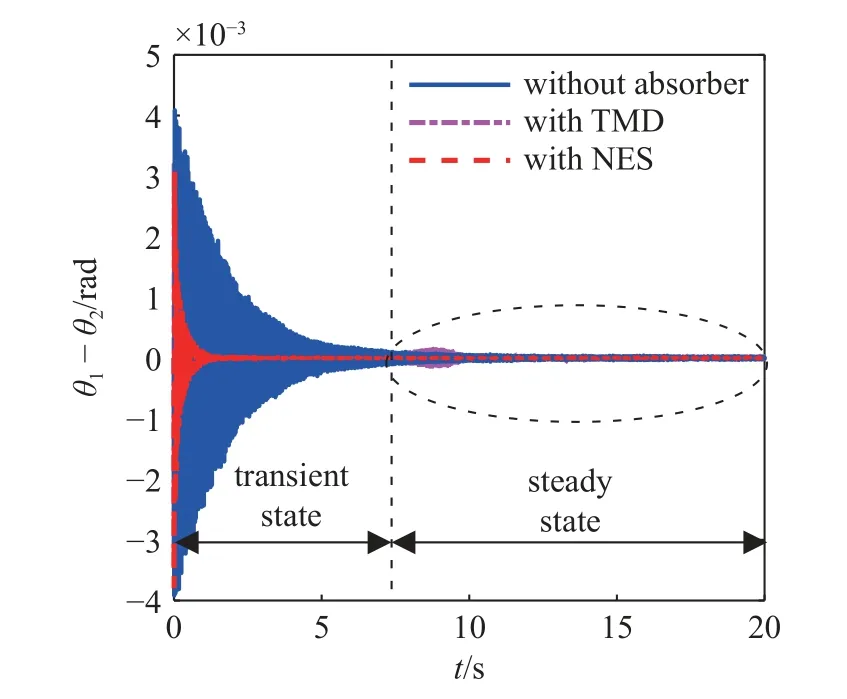
图8 曲轴扭转振动的瞬态和稳态过程Fig.8 Transient and steady-state processes of crankshaft torsional vibration

VI的大小可以直观反映DVA 性能的强弱,为了进一步衡量NES 和TMD 的性能差异,定义性能领先效率函数(performance lead efficiency,PLE).它的表达式见下.PLE的数值越大,表示其中一个减振器性能领先另一减振器性能的程度越大

其中,i代表总的仿真次数,j代表TMD 或NES 领先另一方的次数.

DVA 的鲁棒性用相邻两工况间VI的波动率(fluctuation ratio,FR)表示如下,FR值越小,DVA 的鲁棒性越强

其中,k表示第k个仿真工况.

3.1 DVA 的设计刚度及阻尼对VI 的影响

图9 展示了在不同的设计刚度和阻尼下,耦合NES 和TMD 对VI的影响.其中图9(a) 表示耦合NES,图9(b)表示耦合TMD.从图9(a)中可以发现,当阻尼的量级在101以内时,曲轴振动烈度范围维持在0.9～1.3 之间,这说明,低阻尼状态下,NES不但失效,甚至会恶化曲轴的扭转振动.根据这一点,可以划出其对曲轴扭转振动的阻尼失效区间.另一方面,图中的两条红线分别表示 NES 的最佳刚度和最佳阻尼线,由于NES 的最佳刚度随阻尼发生变化,所以它是一条倾斜的线,而NES 无论在哪种刚度下,其阻尼总是在103量级处取得最优解,所以体现为水平的线.这也说明NES 具有很强的阻尼依赖性.两条红色实线的交点1 为NES 最优刚度和最优阻尼的量级: 1011和103.

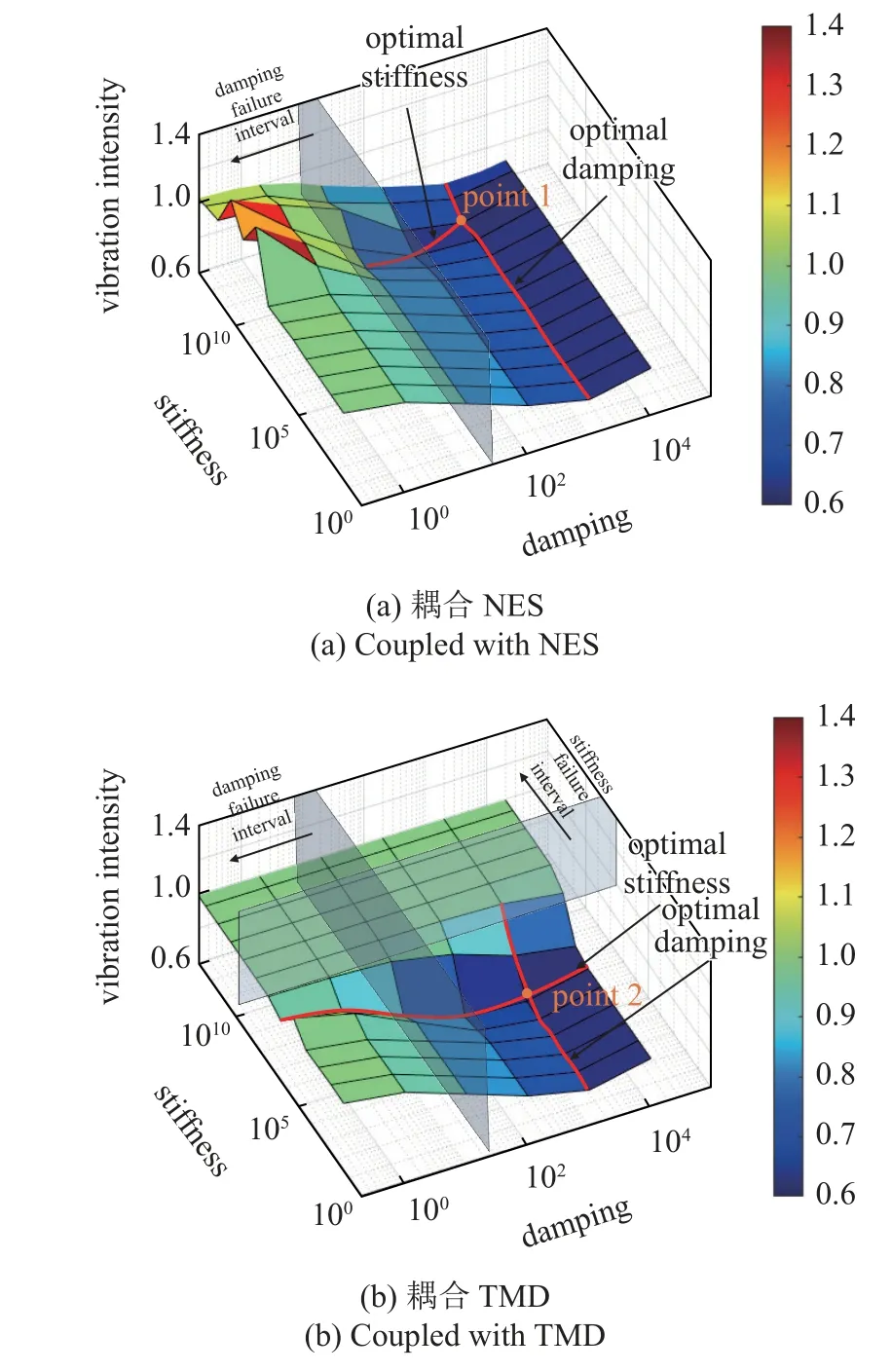
图9 DVA 设计刚度及阻尼对VI 的影响Fig.9 The influence of DVA stiffness and damping on VI

从图9(b)可以发现,与NES 不同的是,TMD 不仅有阻尼失效区间,还有刚度失效区间.当TMD 的刚度数量级调整在109以上时,曲轴扭振的振动烈度将始终维持在0.992 5 处,这意味着此时TMD基本失效,呈现出阻尼和刚度无关性,我们定义这段区间为刚度失效区间.除此之外,可以发现,随着刚度的变化,TMD 总是在105～106刚度量级附近取得最佳的减振性能,这说明TMD 具有较强的刚度依赖性,这也与4190 柴油机曲轴实际的扭振减振器的设计刚度相吻合[32].图中两红线的交点2 为TMD 的最优刚度和最优阻尼的量级: 105和103.

图10 为综合考虑不同阻尼下的VI 随设计刚度变化的示意图.紫色点划线代表耦合TMD,红色虚线代表耦合NES.两线之间围成的区域代表PLE.红色区域代表NES 领先TMD 的效率,紫色区域代表TMD 领先NES 的效率.可以发现,TMD 和NES 随刚度量级变化的过程中,均是先经历一段平稳区域,之后达到最优刚度处.最后,随着刚度量级的持续增加,TMD 的减振性能发生突变,急剧恶化,最后到达刚度失效区.NES 则随着刚度的持续增加,减振性能同样恶化,但相较于TMD,其变化相对平缓.其次,在刚度量级为106.6处有临界刚度,低于该临界刚度时,TMD 减振性能更佳,高于该临界刚度时,NES 减振性能更佳.TMD 在106刚度量级附近有最优刚度,NES 在1011刚度量级附近有最优刚度.

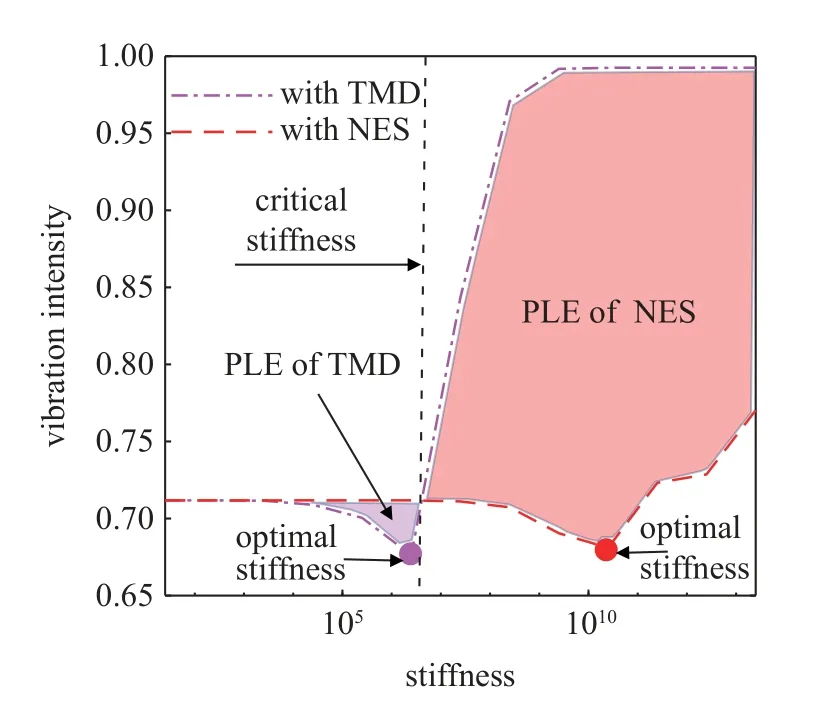
图10 DVA 设计刚度对VI 的影响Fig.10 The influence of DVA stiffness on VI

图11 为综合考虑不同刚度下的VI随设计阻尼变化的示意图.TMD 和NES 控制下的VI值随着阻尼的增大均经历了先减小后增加的过程.这说明,小阻尼无法满足减振器的耗能要求.以101量级为临界阻尼,弱阻尼条件下,NES 的VI值超过了1,这说明此时NES 不但没有减振反而恶化了曲轴本身的扭转振动,而TMD 在此时的VI值是小于1 的,这说明此时TMD 对曲轴的扭振依然有微弱的减振能力.由此可以判断,弱阻尼条件下,NES 失效,TMD 依然发挥作用.超过临界阻尼之后,NES 的性能反超TMD,且两种吸振器同时在103～104阻尼量级范围内减振性能达到最优.超过该量级范围,TMD 和NES 的减振性能同时恶化.

图11 DVA 设计阻尼对VI 的影响Fig.11 The influence of DVA damping on VI

3.2 DVA 的位置排布对VI 的影响

本节将探究DVA 在曲轴上不同的连接位置对不同轴段的扭转振动的影响.如图12 所示,将DVA分别连接到J1～J10上,总共可以得到10 种不同的位置排布方式.J1为曲轴自由端,J10为曲轴功率输出端.

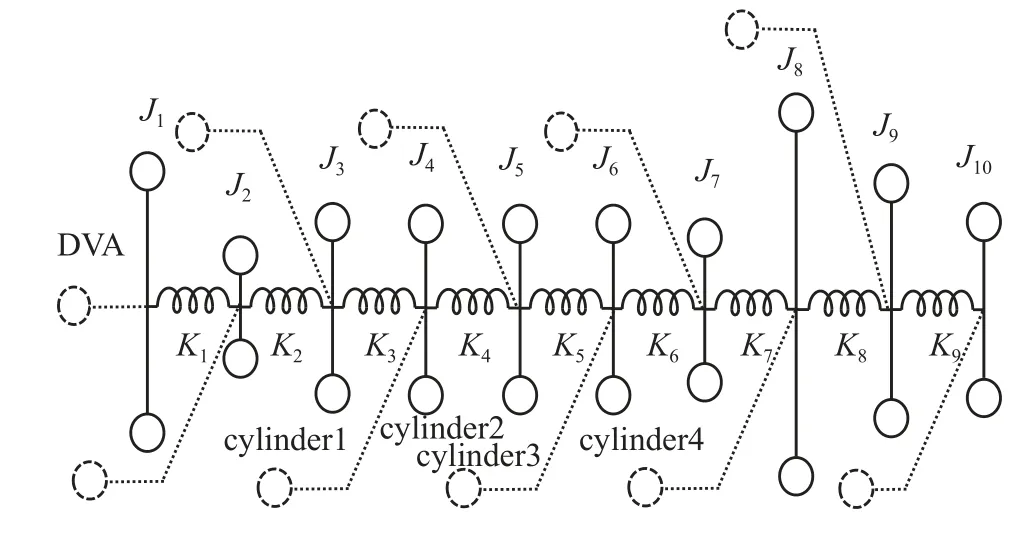
图12 DVA 的位置排布示意图Fig.12 Position arrangement diagram of DVA

观察不同DVA 耦合位置和不同轴段位置下的VI值,如图13 所示.横坐标编号1～10 表示将DVA依次连接到J1～J10上,1～9 表示轴段K1～K9.可以发现,当TMD 与NES 耦合到曲轴上时,曲轴在自由端附近的振动强度较低.同时,改变DVA 的位置对8 轴和9 轴段的影响总是最大的.另外,将TMD 耦合到曲轴的自由端,可以更有效地控制曲轴的扭振,这解释了实际柴油机曲轴的扭振减振器总是在自由端附近.值得注意的是,耦合NES 时,VI的变化趋势与TMD 整体上相同.也就是说,NES 也应该安装在曲轴的自由端附近.当TMD 与J9连接时,8 轴段的振动强度不仅没有降低,反而严重恶化.这是因为此处靠近飞轮,对该处的细微变化会导致曲轴模态发生显著改变.从而导致TMD 的减振效率大幅降低.然而,当在同一位置用NES 代替TMD 时,NES 对该轴段的减振仍然有效.

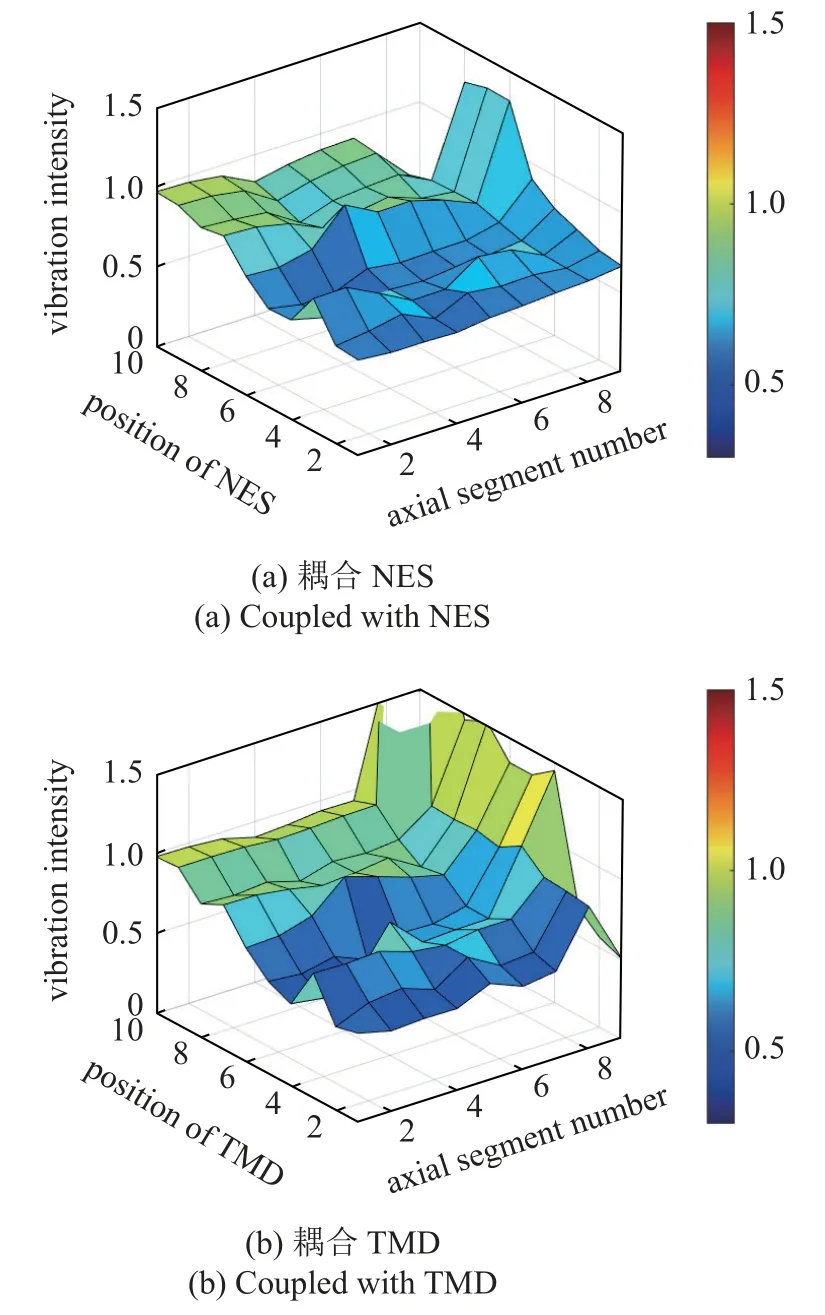
图13 改变DVA 位置排布在不同轴段位置处对VI 的影响Fig.13 The effect of changing the DVA position arrangement at different coaxial segment positions on VI

图14 为综合考虑各个轴段的VI随DVA 位置分布变化的示意图.可以发现,以J2为临界位置,在此之前,TMD 效率高于NES,在此之后,NES 效率高于TMD.

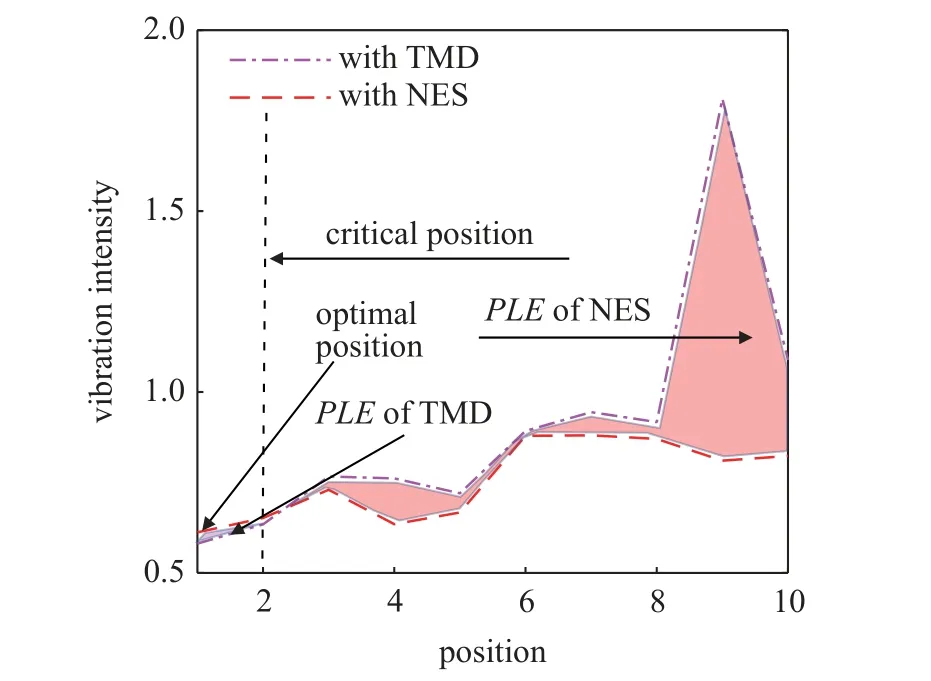
图14 综合考虑各轴段振动时不同DVA 排布对的VI 的影响Fig.14 The influence of different DVA arrangement on VI of each axial segment is considered comprehensively

对前文的VI值进一步分析,根据式(28)～式(29),可以分别计算得到3 种工况 (变刚度、变阻尼以及变位置) 下的PLE和FR.计算得到的结果如图15所示.图15(a)展示了不同工况下NES 和TMD 的PLE的对比示意图,图15(b)则展示了FR的对比示意图.可以发现,改变刚度、阻尼以及位置时,NES 和TMD的减振性能互有领先.但NES 领先TMD 时,其领先优势更大,分别达到了35.4%,9.7%和28.3%.同时NES 的鲁棒性在变刚度及变位置时更有优势,其性能波动率分别为1.3%和8.9%.

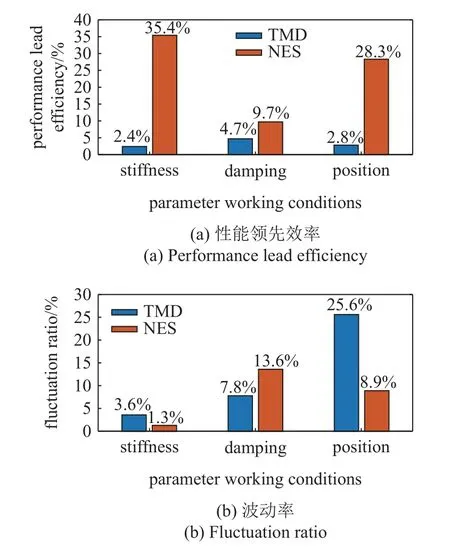
图15 不同工况下DVA 性能对比示意图Fig.15 Comparison diagram of DVA performance under different working conditions

4 结论

本文针对4190 柴油机曲轴建立了M-NCSCO模型,并通过实验验证了模型的正确性.在此基础上,开展了TMD 和NES 对闭环曲轴扭振抑振性能的对比研究.定量给出了NES 和TMD 在不同设计参数条件下的VI,PLE 和FR.结果表明:

(1)在改变减振器刚度、阻尼及位置状态下,TMD 和NES 的PLE分别为2.4%,4.7%,2.8%和35.4%,9.7%,28.3%;TMD 和NES 的FR分别为3.6%,7.8%,25.6%和1.3%,13.6%,8.9%;

(2)使用NES 和TMD 控制曲轴扭振时,NES 具有较高的阻尼依赖性,TMD 具有较高的刚度及位置依赖性;

(3)在曲轴扭振抑振中,低刚度和弱阻尼条件下,NES 吸振效率弱于TMD;高刚度和强阻尼条件下,NES 吸振效率反超TMD.