应力波作用下隧洞顶板围岩块体失稳滑动解析理论研究1)

王 晓

(山东科技大学能源与矿业工程学院,山东青岛 266590)

引言

天然岩体中存在大量节理、裂隙等软弱结构面,这些结构面和隧洞开挖面将隧洞围岩切割成不同形状和大小的块体[1-2].通常,这些块体在自重条件下会保持稳定状态或受限状态[3];然而,它们很容易受到外部动载的干扰,如爆破振动和地震,在动载应力波作用下,隧洞围岩块体的稳定性受到破坏,进而容易失稳滑动,导致隧洞块体坠落或坍塌[4-7].因此,研究隧洞围岩在动载应力波作用下的稳定性具有重要的工程意义.

目前,隧洞围岩的动力稳定性评价一般采用数值模拟、室内试验和理论分析等方法.常用且有效的数值模拟方法是离散元法(DEM)或相关的混合方法,例如有限元法(FEM)-DEM[8].在DEM 模型中,围岩块体可以移动、旋转和变形,节理表面可以被压密、张开或滑动.文献[9-12]均采用DEM 模型来模拟和研究隧洞围岩的动态稳定性.由于节理设置的限制,很少在块体系统中进行隧洞模型试验,Aydan 等[13]报道了关于地下结构在块状介质和非块状介质中的响应和稳定性的一些实验结果,发现在块状介质的隧洞更容易坍塌,特别是在浅层地下隧洞的情况下;李杰等[14]研制了深埋洞室地冲击效应真三维模拟试验系统,对深部巷道在动静载组合作用下的响应机制进行研究,结果显示地冲击扰动可激活深埋岩体中构造岩块运动,造成工程局部严重破坏.块体岩体的结构稳定性通常采用落锤试验进行分析,主要包括块体结构面的超低摩擦效应和块体的滑动位移[15-17].与数值模拟方法和实验方法相比,解析理论方法可以提供更高精度的解,揭示岩体失稳滑动的物理性质.目前,考虑隧洞中块体行为的分析方法主要基于块体理论,但目前块体理论主要用于分析块体在静载荷下的稳定性.尽管部分研究通过块体理论结合拟静力方法、Newmark 方法或其他方法来解决岩块动力学问题[18-20],但仍然不能完全反映动载应力波与围岩块体之间的相互作用特征.

事实上,隧洞围岩在动载荷作用下的松动、滑动或坍塌与块体结构面的力学性质、围压和应力波特性密切相关.一般认为,应力波在工程岩体中的传播包括两个相互关联、相互影响的复杂耦合过程.一方面,由于块体之间不连续面的阻挡,应力波的振幅和能量逐渐衰减.另一方面,应力波在岩体中的传播导致结构面的法向闭合和切向滑动,从而导致隧洞围岩块体的坠落或坍塌.目前,许多学者基于分析方法探讨了应力波与岩体中不连续面之间的相互作用特征.例如,Schoenberg[21]、Li 等[22]以及Pyrak-Nolte 等[23]基于位移不连续法分析了应力波在单个或多个节理的传播特征;利用特征线法和位移不连续理论,Zhao 等[24-25]研究了入射P 波在单个或一组平行节理上的传播;Li 等[26]提出了时域递归方法来分析波在一组平行节理上的传播;刘婷婷等[27]基于时域递归分析法,考虑节理的非线性特性,分析了P 波斜入射一组平行节理的能量传递规律;Wang 等[28]考虑填充介质的黏弹性行为,建立了SH 波在填充黏弹性节理中传播的时域递推方法.这些研究为分析隧洞围岩在应力波作用下的响应规律提供了重要的参考.

针对上述研究现状,本文通过解析理论方法对隧洞围岩顶板块体的失稳滑动行为进行研究,从而进一步阐明隧洞围岩顶板块体动力失稳机理和特征.首先,基于应力波传播理论构建隧洞围岩顶板矩形关键块体失稳滑动解析模型,在解析模型中考虑块体间节理的不同闭合−张开模式,即: 节理闭合不滑动、节理闭合滑动和节理张开滑动,并采用线弹性模型和库仑滑移模型来描述节理的法向和切向行为.其次,基于UDEC 数值模型验证所推导解析模型的有效性和可靠性.最后,基于解析模型探讨节理属性、应力波特征和岩块属性等参数对围岩块体滑动位移、块体间结构面闭合−张开特征的影响,并阐明不同参数影响下围岩块体失稳滑动差异性.

1 隧洞围岩块体类型及破坏形式

天然岩体中存在大量节理裂隙等软弱结构面,这些结构面和隧洞开挖面将隧洞围岩切割成不同形状和大小的块体,如图1 所示.根据块体的边界条件(如几何形态及其与隧洞自由面的位置关系),可以将围岩块体分为无限块体和有限块体[1-2].无限块体是指未被结构面和临空面完全切割成孤立体的块体,仍有部分与母岩相连.一般而言,该类块体不会产生失稳问题,但当外界载荷作用力超过岩体的强度时,该类块体可能发生剪切、张拉破坏,进而诱使围岩发生劈裂、剥落与岩爆等灾害.有限块体是指被结构面和临空面完全切割成孤立体的岩块,或称分离体.有限块体可以划分为可动块体和稳定块体.稳定块体是指在工程作用力和自重作用下,即使滑移面的抗剪强度等于零仍可以保持稳定的块体,如楔形块体.可动块体是指可沿空间某一个或若干个方向移动而不受相邻块体阻碍的块体.可动块体则包含关键块体和潜在的关键块体.关键块体是指在工程作用力和自重作用下,由于滑动面上的抗剪强度难以抵御滑动力,若不施加工程措施,必将失稳的块体.潜在的关键块体是在工程作用力和自重作用下,由于滑动面有足够的抗剪强度保持稳定,而在滑动面上的抗剪强度降低可能失稳的块体.一般情况下,关键块体和潜在关键块体均称之为关键块体.值得说明的是,当外界作用力大于岩块的强度时,有限块体也会发生块体碎裂、剥离等脆性破坏.

总体而言,在无支护条件下,隧洞围岩的失稳与围岩块体类型、动载荷强度有关.对于可移动关键块体,其主要的失稳形式为块体失稳滑移,需要进一步说明的是,一旦围岩关键块体滑动后,其他非关键块体也可能会变成关键块体而滑动;对于不可移动块体以及无限块体,块体可能因动载荷强度过大而产生拉伸、剪切等破坏.当然,在高地应力条件下,可移动关键块体也可能产生拉伸、剪切等破坏.表1汇总了不同隧洞围岩块体类型的主要失稳破坏形式.

值得说明的是,本文的研究着重于分析浅埋条件下隧洞顶板围岩关键块体在应力波扰动作用下的失稳滑动机理和特征,不考虑围岩块体的破坏,即假设应力波作用下围岩关键块体的失稳仅表现为块体的滑动.

2 隧洞围岩关键块体动力失稳滑动理论分析

由于隧洞围岩块体的无规则性,应力波到达围岩块体时会发生复杂透射和反射行为,会改变块体的法向和切向受力状态,当围岩块体的滑动力(重力、动态滑动力)大于块体的界面摩擦力时,块体就会失稳滑动.由于应力波与复杂块体形状的相互作用机理非常复杂,理论解答较难实现,因此本节的理论分析主要针对应力波垂直入射作用下隧洞围岩顶板矩形关键块体的失稳滑动.

2.1 理论解析模型

假设在如图1 所示的二维节理岩体中开挖隧洞,此时在隧洞顶部形成由岩石节理和隧洞开挖面切割的相对简单的矩形关键块体.在重力G作用下,该关键块体处于稳定状态,如图2(a)所示,即G≤2F0,其中F0=N0tanφ代表块体节理面的抗滑力,N0和φ代表块体节理面受到的初始法向压力以及节理的摩擦角.假设一应力波(以P 波为例)由块体左侧节理面(节理#L)垂直穿过该块体,该块体的初始受力平衡状态将会被打破,此时的受力状态如图2(b)所示.假设应力波作用下节理面不产生磨损,即应力波作用下节理摩擦角不变,当G≤FdL+FdR(FdL=(N0+NdL)tanφ,FdR=(N0+NdR)tanφ代表块体节理面(节理#L 和节理#R) 的动态抗滑摩擦力;NdL和NdR代表节理面受到的动态法向压力)时,块体仍然处于稳定状态;但是,当G＞FdL+FdR时,块体将会失稳滑动.

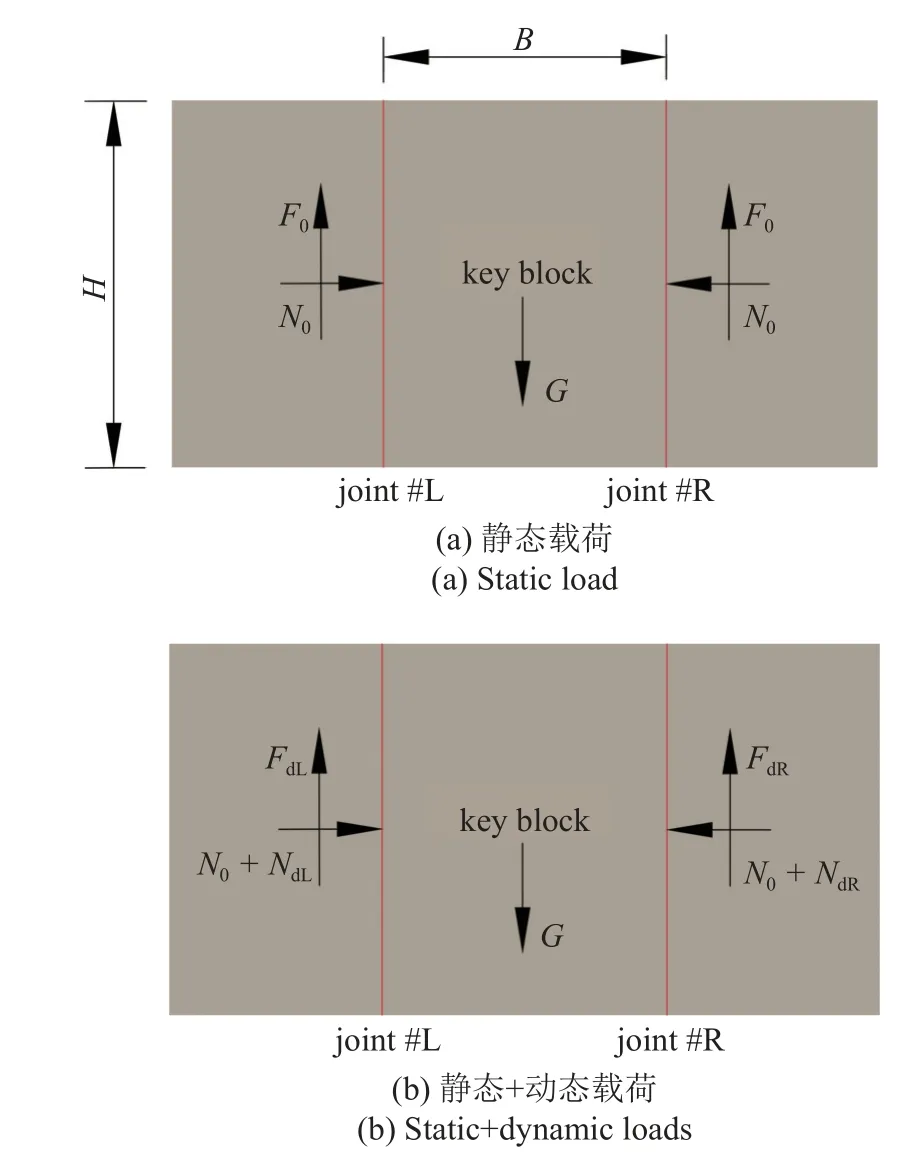
图2 应力波垂直入射围岩顶板矩形关键块体受力分析Fig.2 Stress of rectangular key block on the roof of surrounding rock under stress wave vertical incidence

在垂直入射应力波作用下,图2 所示矩形关键块体左、右侧的节理(假设节理的法向和切向行为符合线弹性模型和库仑滑移模型)将会经历2 种状态: 闭合和张开(如图3 所示).若节理张开,该节理不再提供摩擦力;若节理闭合,且闭合量增加时(法向应力增加),该节理提供的摩擦应力也会增加,但是,当闭合量逐渐减小(法向应力逐渐降低),该节理提供的摩擦力会逐渐减小.此外,节理的闭合−张开行为也会影响应力波的应力传递.通常在分析波传播过程时,块体之间的节理被视为边界条件[17-24].当节理闭合时,将节理模拟为连续应力和不连续位移的边界条件.此时,左行波(例如,,其中j=L 或R,表示块体的节理#L 或节理#R;“−”和“+”代表节理的左侧面和右侧面) 和右行波(例如)是反射波和透射波的叠加.当节理张开时,将节理模拟为零应力边界条件,P 波只能在节理界面发生反射.此时,节理面上的左行波和右行波仅与反射波叠加.节理的不同变形模式决定了节理的应力状态,当节理的抗滑力小于关键块体的重力时,块体将向下滑动.因此,图2 所示矩形关键块体的失稳滑动与否与应力波引起块体间节理变形模式有关,可以通过分析块体间节理的不同变形模式进而求解关键块体的滑动位移.

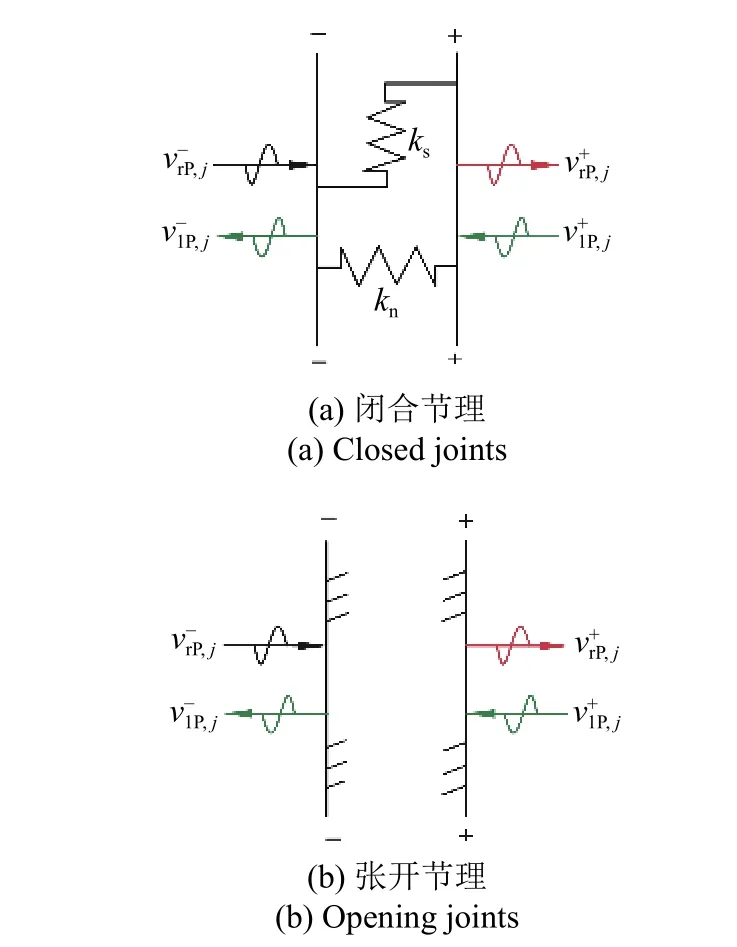
图3 块体间节理闭合−张开特征Fig.3 Closure-opening characteristics of joints between blocks

一般而言,上述矩形关键块体在不同的节理变形模式下具有以下运动形式.

情况1: 块体左侧节理#L 以及右侧节理#R 处于闭合状态,块体不滑动,即 Δun,j≥−Δun0,且G≤FdL+FdR.此时,块体两侧的节理法向满足应力连续、位移不连续的边界条件,即

需要说明的是这种情况下块体结构面会产生一定的剪切变形 Δuτ0=τ/ks(式中,τ 为结构面受到的剪应力,ks为结构面的切向刚度),但是这里不计入块体的滑动位移中.

方程(2)对时间t的差分形式可以写为

为了便于计算,方程式(4)的差分形式可以写为

情况2: 块体左侧节理#L 以及右侧节理#R 处于闭合状态,块体滑动,即 Δun,j≥−Δun0,且G＞FdL+FdR.此时,块体两侧的节理法向也满足应力连续、位移不连续的边界条件,即

这种情况下,块体的滑动速度为

情况3: 块体一侧节理处于张开状态,此时,块体是否滑动取决于未张开节理的边界条件,可根据情况1 和情况2 进行判断.当未张开节的摩擦力满足情况1 的条件时,块体滑动按照方程(3)获得;满足块体滑动情况2 的条件时,块体的滑动速度可根据方程式(8)获得.

情况4: 块体两侧节理均处于张开状态,即Δun,j＜−Δun0.此时,块体两侧的节理的边界条件为

这种情况下,块体失去了摩擦力作用,以自由落体或抛体运行掉落,滑动速度为

式中,g为重力加速度.

截止这里,块体间节理的变形模式以及块体的滑动特征已经确定.接下来,需要计算上述方程的参数.

如图2 所示,由于块体有一定宽度B,P 波穿过该块体 时所消耗的时 间为 ΔtP=B/CP,其中CP为P 波在岩体中的传播速度.当P 波垂直节理面由节理#L 入射时,块体左侧节理#L 和右侧节理#R 满足:

节理左侧面和右侧面上的法向应力和法向速度可以表示为[29]

式中,ZP=ρCP为P 波的波阻抗.

将方程(11)代入方程(1)、式(2)、式(6)～式(7)和式(9),上述4 种情况下的波传播方程可以求得.

对于情况1 和情况2

式中,方程的系数A1=B1=C1=D1=ZP,E1=Zp−knΔt,F1=ZP+knΔt,G1=knΔt,H1=−knΔt.

对于情况3 和情况4 中的张开节理

式中,方程的系数A2=B2=ZP.

将方程(12)～式(15)代入方程(11),任意时刻节理#L 和节理#R 的法向应力和法向速度可以求得.随后,节理#L 或节理#R 的相对法向位移可以求得

同时,块体的滑动位移可通过方程(3)、式(8)和式(10)获得

2.2 理论模型验算

为了验证上述分析模型的有效性和可靠性,使用UDEC 数值软件建立了与理论分析模型相同的数值模型(如图4 所示)进行对比分析.UDEC 是一款比较成熟的商业软件,许多研究表明采用UDEC 研究应力波作用下节理岩体的响应特征是可靠的[11].在理论和UDEC 模型中,岩块和节理基本力学参数参照Bandis 等[30]对砂岩的实验研究结果进行取值,如表2 所示;关键块体设为正方形,尺度按照IV 结构面的范围进行取值[31],设边长为0.5 m;重力加速度设为9.8 m/s2.

表2 岩块及节理力学属性Table 2 Mechanical properties of rock block and joints

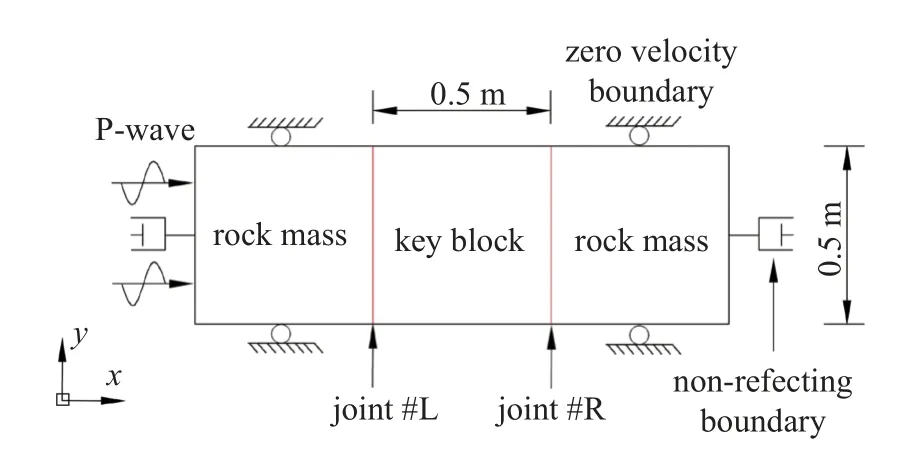
图4 理论验算UDEC 模型Fig.4 Theoretical verification UDEC model

假设入射波为P 波,且从块体左侧节理#L 垂直入射,入射波简化为正弦波形,即

式中,Ai为P 波的入射振幅,mm/s;w=2πf为入射波的角频率,rad/s;f为入射波的频率,Hz;t和td为时间以及波加载时间.这里,入射波的振幅A、频率f和持续时间td设定为200 mm/s,50 Hz 以及1/fs.

图5 比较了P 波通过块体后的波形、块体节理#L 和节理#R 的相对法向变形以及块体滑动运动的理论解析和数值结果.在该分析中,块体节理面初始法向应力为1.0 MPa.从图中可以看出,用解析方法得到的P 波传播波形、块体间节理的张开、闭合特征(当 Δun+Δun0≥ 0,对应图中曲线大于0 的时刻,节理处于闭合状态;当 Δun+Δun0＜ 0,对应图中曲线小于0 的时刻,节理处于张开状态)以及块体的滑动位移与UDEC 数值方法基本一致.由于UDEC 模型中波由模型左侧传播到块体具有一定的距离,因此呈现出时间略微滞后的现象.此外,由于模型突然的闭合−闭合−张开,UDEC 模型呈现出了震荡现象,可能的原因是,由于应力波作用时间和作用强度的不同,块体左右两侧节理的摩擦力并不一致,导致块体呈现出轻微的转动现象(转动位移小于节理的最大张开位移),而理论分析模型没有考虑块体的这一现象.总体而言,本节所推导的应力波垂直入射隧洞顶板围岩关键块体滑动理论分析模型是可靠的,采用上述分析模型可以求解不同参数条件下应力波垂直入射隧洞顶板围岩矩形关键块体的滑动特征.

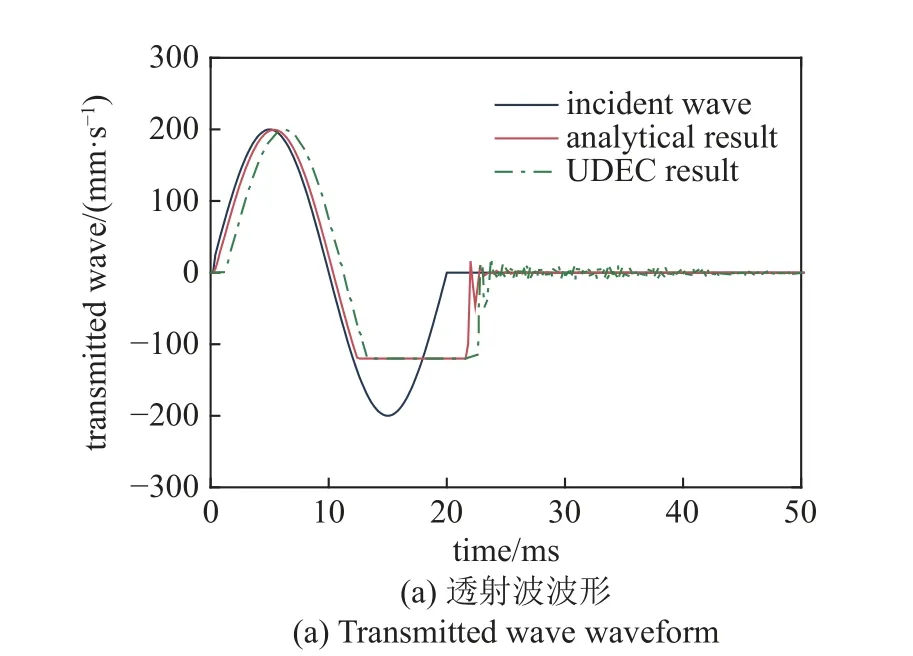
图5 理论解析和数值结果的对比分析Fig.5 Comparative analysis of theoretical and numerical results

2.3 参数分析

本节基于上述解析理论模型探究不同节理初始法向应力、不同节理法向刚度、不同节理摩擦角、不同入射波振幅、不同入射波频率、不同块体岩性以及不同块体的尺寸对应力波垂直入射条件下隧洞顶板围岩矩形关键块体滑动特征的影响.

2.3.1 节理初始法向应力的影响

由于埋深、地质结构以及开挖对工程岩体的影响,地下隧洞围岩块体结构面的张开、闭合程度不同,受到的初始法向应力也不同.参考Dai 等[5]对某一砂岩动力冲击滑动实验研究中结构面初始法向应力的取值,本文假设隧洞(浅埋情况)围岩块体节理面的初始法向应力为0.4,0.6,0.8 以及1.0 MPa 来分析节理初始法向应力对隧洞围岩顶板矩形关键块体动力失稳滑动特征的影响.块体假设是方形的,边长为0.5 m;节理的法向刚度为5 GPa/m,岩块和节理的其他参数与表2 所列相同;P 波的振幅、频率和持续时间分别为150 mm/s,50 Hz 和1/fs.

图6 显示了P 波垂直入射作用下不同节理初始法向应力对隧洞顶板矩形关键块体滑动位移的影响.由图可知,块体的滑动位移与节理面受到的初始法向应力密切相关.随着节理初始法向应力的增加,块体的滑动位移逐渐减小.节理初始法向应力为0.4,0.6,0.8 以及1.0 MPa 所对应的块体滑动位移分别为1.57,0.575,0.214 以及0.068 mm.节理初始法向应力对块体稳定性的影响体现在两个方面: 一是限制块体间节理的张开;二是提供摩擦力阻止块体滑动.当然,当块体两侧节理都张开时,块体的摩擦力为零.图7 显示了不同节理面初始法向应力条件下块体间节理的闭合−张开特征.图中,J#L 和J#R 分别代表左侧节理和右侧节理,当节理张开闭合曲线大于0 时,代表节理处于闭合状态,如灰色部分描述;当节理张开闭合曲线小于0 时,代表节理处于张开状态,且蓝色部分代表两侧节理均张开、粉色部分代表单一节理张开,下同.由图可知,随着初始法向应力的增加,块体两侧节理面的张开时间逐渐减少(节理初始法向应力为0.4,0.6,0.8 以及1.0 MPa 所对应的块体间节理面的张开时间分别为19.3,11.9,7.8 以及3.9 ms,其中双节理同时张开的时间占比分别为67.9%,66.4%,62.2%和58.9%),即块体自由下落或超低摩擦滑动的时间减少,导致块体滑动位移减小.

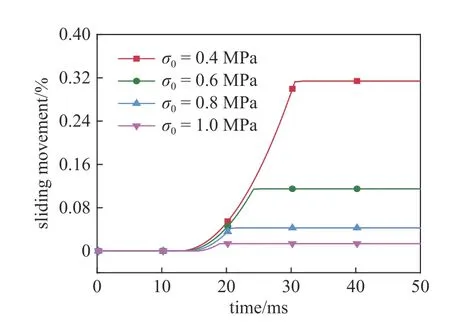
图6 初始法向应力对块体滑动位移的影响Fig.6 Effect of initial normal stress on block slide displacement

图7 不同节理初始法向应力条件下块体间节理的闭合−张开特征Fig.7 Close-open characteristics of joints between blocks under different initial normal stress

2.3.2 节理法向刚度的影响

参考Bandis 等[30]对几种岩石节理的实验研究,取节理的法向刚度为5,20,35 以及50 GPa/m 来探究节理法向刚度对隧洞顶板围岩矩形关键块体动力失稳滑动位移的影响.岩块和节理的其他参数与表2所列相同;P 波的振幅、频率和持续时间分别为150 mm/s,50 Hz 和1/fs;块体为方形,边长为0.5 m;块体间节理的初始法向应力为0.8 MPa.

图8 显示了不同节理法向刚度对隧洞围岩顶板矩形关键块体失稳滑动的影响.由图可知,块体的滑动位移随节理法向刚度的增大而增大.节理法向刚度为5,20,35 以及50 GPa/m所对应的块体滑动位移分别为0.214,0.357,0.375 以及0.382 mm.Deng 等[11]的数值研究也存在这一现象,他们的研究结果表明在其他参数不变的条件下,节理法向刚度越大,隧洞围岩块体更容易失稳滑动,失稳破坏区越大.主要的原因可能是节理的法向刚度越小,节理的初始闭合量越大,应力波在节理张开过程中消耗的能量增加.图9 显示了不同节理面初始法向刚度条件下块体间节理的闭合−张开特征.由图可知,对于P 波垂直入射矩形块体而言,随着节理法向刚度的增加,块体间节理面的张开时间逐渐增加,导致块体的滑动位移也增加.另外,还可以看出随着节理法向刚度的不断增加,块体的动力滑动位移增量以及块体间节理面的张开时间(节理刚度为5,20,35 以及50 GPa/m 所对应的节理张开时间分别为7.8,9.4,9.6 以及9.65 ms,其中双节理同时张开的时间占比分别为62.2%,79.8%,86.4% 以及87.1%) 有明显减小的趋势.

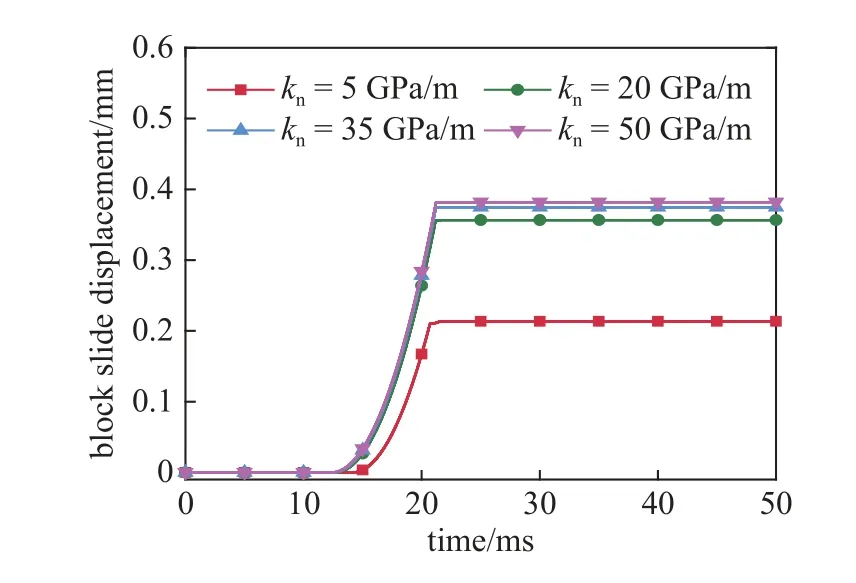
图8 节理法向刚度对块体滑动位移的影响Fig.8 Effect of normal stiffness of joints on block slide displacement

图9 不同节理法向刚度条件下块体间节理的闭合−张开特征Fig.9 Close-open characteristics of joints between blocks under different joint normal stiffness

2.3.3 节理摩擦角的影响

节理摩擦角是影响围岩块体失稳滑动的因素之一.本节选取围岩块体2 侧节理面的摩擦角为25°,30°,35°以及40 °来探讨节理摩擦角对隧洞围岩顶板矩形关键块体动力失稳滑动特征的影响.节理的法向刚度为5 GPa/m,岩块和节理的其他参数与表2所列相同.P 波的振幅、频率和持续时间分别为150 mm/s,50 Hz 和1/fs;块体为方形,边长为0.5 m;块体间节理的初始法向应力为0.8 MPa.

由图10 可知,随着节理摩擦角的增加,围岩顶板矩形关键块体的滑动位移逐渐降低.节理摩擦角为25°,30°,35°以及40 °所对应的块体滑动位移分别为0.213 9,0.213 5,0.213 2 以及0.213 mm.主要的原因是节理摩擦角越大,在相同的节理法向应力变化条件下,围岩块体间节理的摩擦力越大,导致围岩块体越不容易滑动.此外,不难发现节理摩擦角的变化对块体滑动位移影响较小,主要原因是当应力波足够大时,导致块体滑动较大时刻主要在块体间节理面属于无摩擦(节理完全张开)或超低摩擦(近乎完全张开)阶段,如图11 所示.当结构面处于无摩擦或超低摩擦状态时,节理摩擦角对节理滑动摩擦力的影响相对较小,甚至可以忽略不计.另外,由图11可知,由于节理摩擦角并不控制节理面的法向变形,因此随着节理摩擦角的增大,围岩块体间节理面的张开时间是一致的,这也进一步说明,应力波作用下围岩块体滑动存在2.1 节理论分析模型所述的情况2 和情况3 的状态(情况4 与节理摩擦角无关).相比之下,节理面处于张开无摩擦或近乎张开超低摩擦状态时对隧洞围岩顶板矩形关键块体滑动位移的影响更大.

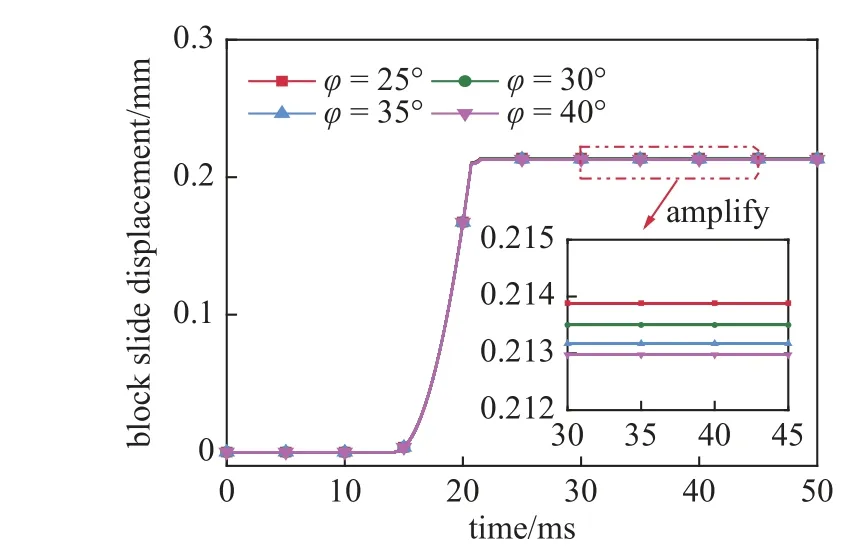
图10 节理摩擦角对块体滑动位移的影响Fig.10 Effect of joint friction on block slide displacement

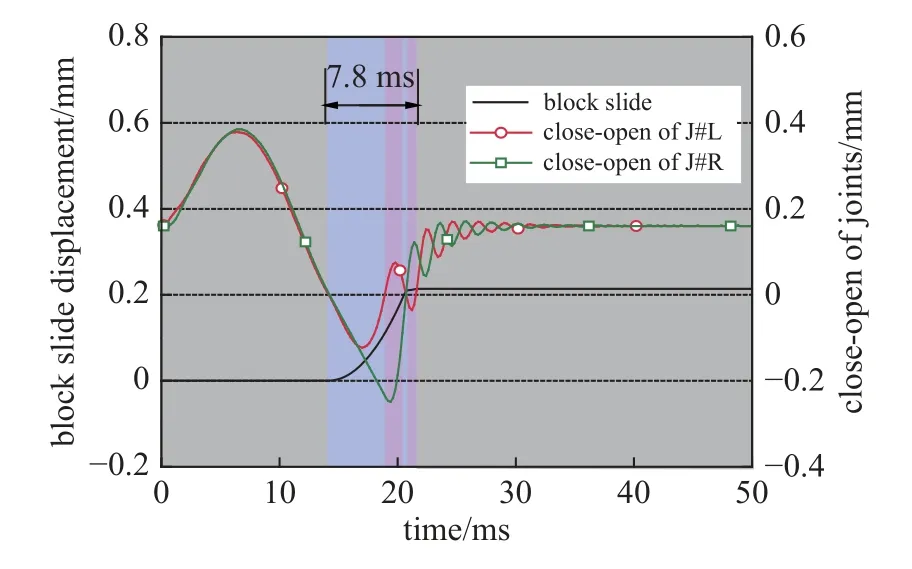
图11 不同节理摩擦角条件下块体间节理的闭合−张开特征Fig.11 Close-open characteristics of joints between blocks under different joint friction angle

2.3.4 入射波振幅的影响

本节选取P 波的振幅为50,100,150 以及200 mm/s 来探讨应力波振幅对隧洞围岩顶板矩形关键块体动力失稳滑动特征的影响.节理的法向刚度为5 GPa/m,岩块和节理的其他参数与表2 所列相同.P 波的频率和持续时间分别为50 Hz 和1/fs;块体为方形,边长为0.5 m;块体间节理的初始法向应力为0.6 MPa.

由图12 可知,随着入射波振幅的增加,块体的滑动位移逐渐增加.入射波振幅为50,100,150 以及200 mm/s 所对应的块体滑动位移分别为0,0.136,0.575 以及1.25 mm.主要原因是P 波的振幅越大,导致块体间节理面越容易张开,且张开时间也会增加,如图13 所示,而围岩块体结构面的张开(无摩擦或超低摩擦)过程时间越长,块体的滑动量越大.入射波振幅为50,100,150 以及200 mm/s 所对应的节理张开时间分别为0,5.7,11.9 以及17.2 ms,其中双节理同时张开的时间占比分别为0%,61.4%,66.4%以及 67.4%.此外,由图13 还可以得知,随着应力波振幅的增加,围岩块体结构面的张开−闭合次数也逐渐增加.

图12 入射波振幅对块体滑动位移的影响Fig.12 Effect of incident wave amplitude on block slide displacement

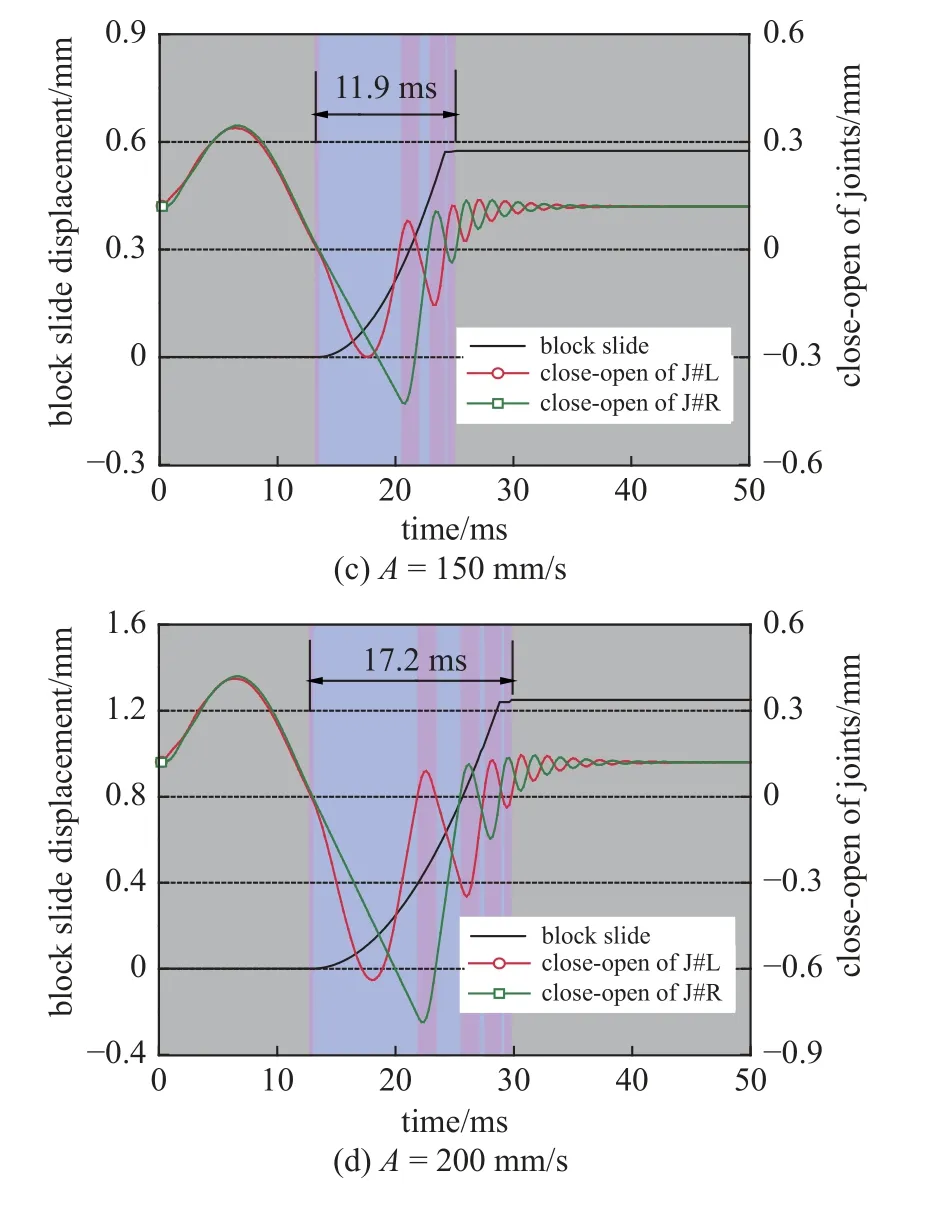
图13 不同入射波振幅条件下块体间节理的闭合−张开特征Fig.13 Close-open characteristics of joints between blocks under different incident wave amplitudes

2.3.5 入射波频率的影响

本节选取40,80,120 以及160 Hz 的频率来探讨应力波频率对隧洞围岩顶板矩形关键块体滑动特征的影响.这里,节理的法向刚度为5 GPa/m,岩块和节理的其他参数与表2 所列相同.P 波的振幅和持续时间分别为150 mm/s 和1/fs;块体为方形,边长为0.5 m;块体间节理的初始法向应力为0.6 MPa.

图14 显示了入射波频率对隧洞围岩顶板矩形关键块体动力失稳滑动的影响.从图中可以看出,随着入射波频率的增加,围岩块体的滑动位移逐渐减小.入射波频率为40,80,120 以及160 Hz 所对应的块体滑动位移分别为0.954,0.183,0.034 以及0.01 mm.相比之下,低频应力波对块体滑动位移的影响要远大于高频应力波的影响.主要原因是应力波的特征频率越低,相同振幅条件下应力波导致的块体间节理的张开时间越长,如图15 所示,入射波频率为40,80,120 以及160 Hz 所对应的节理张开时间分别为15.2,6.4,3.9 以及1.5 ms,其中双节理同时张开的时间占比分别为71.1%,51.6%,38.5%以及0.节理的张开无摩擦或超低摩擦时间越长,块体的滑动位移越大.由此可见,实际工程中应特别注重低频载荷的动力影响,这也与我国的爆破振动规范要求一致[32].此外,由图15 还可得知,应力频率越大,围岩块体间的节理越不容易张开(最大张开位移逐渐降低).

图14 入射波频率对块体滑动位移的影响Fig.14 Effect of incident wave frequency on block slide displacement

图15 不同入射波频率条件下块体间节理的闭合−张开特Fig.15 Close-open characteristics of joints between blocks under different incident wave frequencies

2.3.6 块体岩性的影响

由于矿物组分、沉积环境、风化程度的不同,不同类型岩石的物理力学性质(岩性)也不相同.密度ρ、弹性模量E和泊松比ν是反应岩石物理力学性质的主要参数,这3 个参数与应力波在岩块中的传播速度有关系:因此,可以通过将块体岩性的影响转变为分析岩块纵波波速的影响来分析问题.一般而言,P 波在不同类型岩石中的传播波速在2000～6000 m/s 之间,因此,本小节选取岩石的纵波波速为2500,3500,4500以及5500 m/s 来探究不同岩块岩性对隧洞围岩顶板矩形关键块体失稳滑动特征的影响.在这里,块体是方形的,边长为0.5 m;节理的法向刚度为5 GPa/m,节理的其他参数如表2 所示;P 波的振幅、频率和持续时间分别为150 mm/s,50 Hz 和1/fs.块体间节理的初始法向应力为0.8 MPa.

图16 显示了不同块体岩性条件下隧洞围岩顶板矩形关键块体的滑动位移.由图可知,随着岩块纵波波速的增加,块体的滑动位移逐渐增加.岩块纵波波速为2500,3500,4500 以及5500 m/s 所对应的块体滑动位移分别为0.042,0.276,0.44 以及0.701 mm.主要原因是岩块岩性越好,其与应力波作用时块体间节理更容易闭合−张开,如图17 所示,随着岩块纵波波速的增加,块体间节理的张开时间逐渐增加(岩块纵波波速为2500,3500,4500 以及5500 m/s 所对应的节理张开时间分别为3.1,7.9,10.7 以及13.2 ms,其中双节理同时张开的时间占比分别为51.6%,62.3%,59.8%以及60.1%),导致隧洞围岩顶板矩形关键块体的超低摩擦滑动或自由掉落过程时间增加.

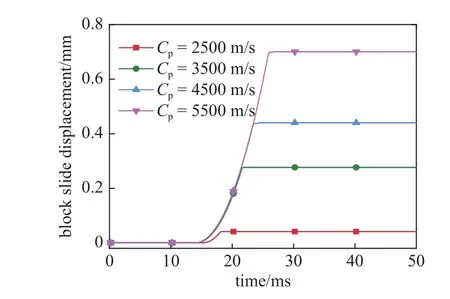
图16 块体岩性对块体滑动位移的影响Fig.16 Effect of block lithology on block slide displacement

图17 不同块体岩性条件下块体间节理的闭合−张开特征Fig.17 Close-open characteristics of inter block joints under different block lithology

2.3.7 块体尺寸的影响

由于地质构造的不同,地下隧洞围岩块体的大小也是不同的.一般而言,对于工程上特别关心的IV级结构面而言,节理的长度一般为数厘米～数十米[26],因此,节理面切割而成的块体边长也在数厘米～数十米之内.考虑到部分隧洞直径在5 m 以下以及为了保证节理和开挖面切割围岩块体的可动性,本节选择块体宽度B(节理间距)分别为0.5,2.0,3.5 和5.0 m 来探究不同块体尺寸对块体滑动位移的影响.同时,假设隧洞围岩的块体为矩形,高度H保持0.5 m 不变.节理的法向刚度为5 GPa/m,节理及岩块的其他参数与表2 所列相同.P 波的振幅、频率和持续时间分别为150 mm/s,50 Hz 和1/fs;块体间节理的初始法向应力为0.8 MPa.

图18 显示了不同块体尺寸条件下隧洞围岩顶板矩形关键块体的滑动位移.由图可知,随着块体尺寸的增加,块体的滑动位移逐渐增加.块体宽度为0.5,2.0,3.5 以及5.0 m 所对应的块体滑动位移分别为0.214,0.267,0.311 以及0.364 mm.可能的原因包括2 个方面: 一是块体的重力增加,二是随着块体尺寸的增加,应力波波长λ(λ=Cp/f≈70 m)与块体尺寸B的比值减小,导致应力波在块体间节理处的响应形式更加复杂,更容易导致块体间节理的张开或超低摩擦滑动时间增加,如图19 所示,块体宽度为0.5,2.0,3.5 和5.0 m 所对应的节理张开时间分别为7.8,8.0,8.3 以及8.8 ms,其中双节理同时张开的时间占比分别为 62.2%,52.5%,43.3% 以及41.2%.由图19 还可知,随着块体尺寸的增加,块体在应力波作用下单节理面张开的时间逐渐增加.

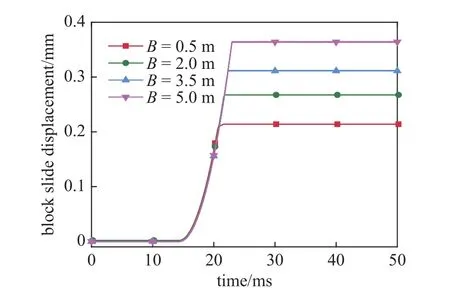
图18 块体宽度对块体滑动位移的影响Fig.18 Effect of block width on block slide displacement

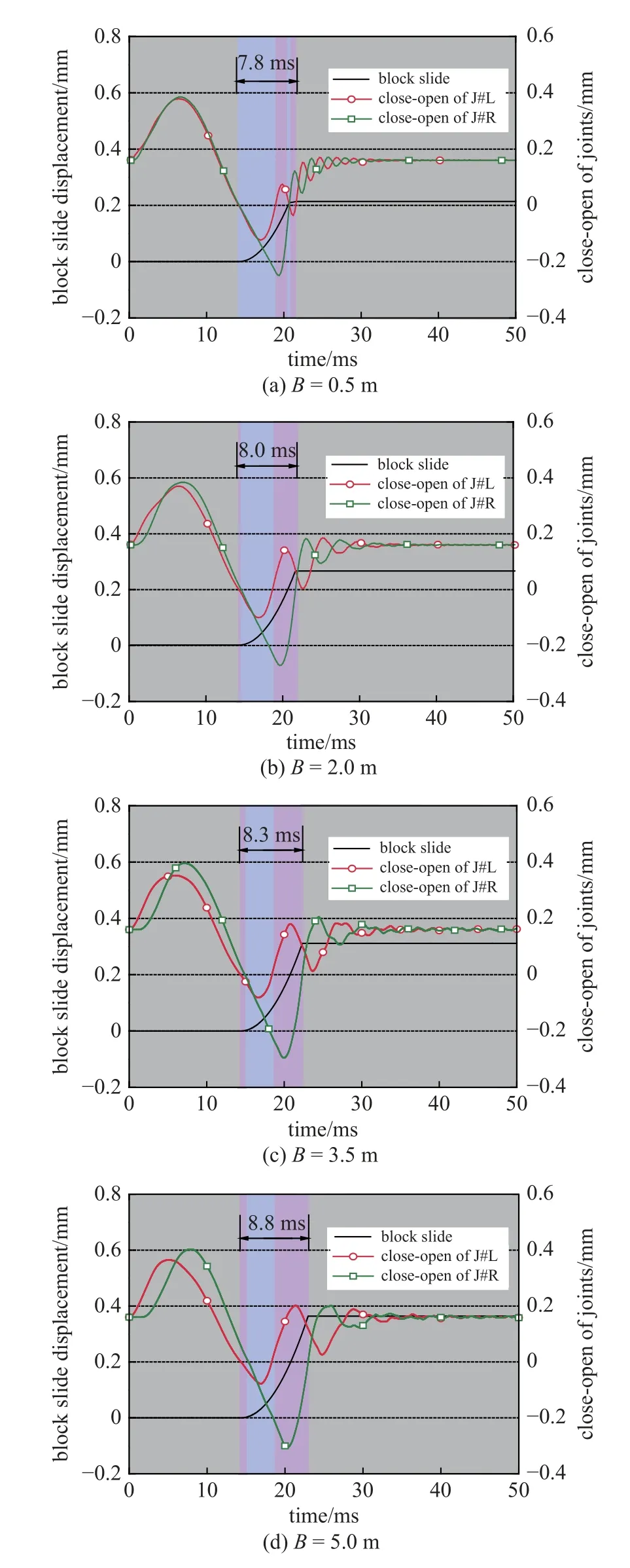
图19 不同块体宽度条件下块体间节理的闭合−张开特征Fig.19 Close-open characteristics of joints between blocks under different block widths

3 讨论

考虑应力波与围岩结构面相互作用进而探究隧洞围岩的失稳滑动特征为揭示隧洞围岩动力失稳垮塌提供了新思路.本文基于应力波传播理论推导了隧洞围岩顶板关键块体动力失稳滑动解析模型.在解析模型中,块体被简化为矩形,位于隧洞顶部,在动态扰动之前处于稳定状态.在计算块体滑动位移过程中,考虑块体间节理的不同闭合−张开模式,并采用线弹性模型和库仑滑移模型来描述节理的法向和切向行为.通过将解析模型与相同的UDEC 模型计算结果进行了比较,验证了解析模型的有效性和可靠性.随后,探讨了节理面初始法向应力、初始法向刚度、摩擦角,应力波的振幅、频率以及块体的岩性、尺度对隧洞顶板围岩矩形关键块体滑动位移、块体间结构面闭合−张开特征的影响.

鉴于应力波与隧洞围岩块体结构面的相互作用机理十分复杂以及笔者水平有限,所推导模型具有一定的使用范围,即: 隧洞围岩顶板关键块体为矩形、应力波垂直块体节理面入射、应力波作用下围岩块体不会产生损伤破坏,也不会造成结构面的磨损,块体的失稳仅为沿着结构面的滑移或自由落体.笔者今后将在应力波与非矩形关键块体相互作用机理上下功夫,此外,也将进一步考虑应力波作用下围岩块体自身的破坏以及结构面的损伤劣化,进一步更加精确地揭示地下隧洞围岩块体动力失稳垮塌机理.

4 结论

(1)本文基于应力波传播理论所推导的隧洞围岩顶板关键块体动力失稳滑动解析模型可以有效地用于计算应力波作用下隧洞围岩顶板矩形关键块体的失稳滑动位移.

(2)在应力波作用下,隧洞围岩块体间节理面会闭合−张开,在张开过程中节理面的摩擦力会逐渐降低,甚至为零,块体间节理面的超低摩擦和无摩擦阶段对块体滑动位移的影响最大.

(3)当应力波垂直作用于围岩块体结构面且强度足以诱使节理面张开时,影响块体滑动位移较大的参数是节理面初始法向应力、应力波振幅、频率和块体岩性,单周期正弦应力波下块体滑动位移的变化在0.659～1.502 mm 之间;其次为节理初始法向刚度、块体尺寸,块体滑动位移的变化在0.15～0.168 mm 之间.

(4)超低摩擦是工程围岩块体动力失稳滑动的主要特征,工程中要特别关心应力波诱发围岩结构面的超低摩擦问题.