海岛输电塔线体系风振响应及易损性分析

曾璧环，池曦锵，张佳毅，杨德栋，曹枚根

（1.温州电力建设有限公司，浙江 温州 325024；2.北方工业大学土木工程学院，北京 100144；3.国网浙江省电力有限公司温州供电公司，浙江 温州 325000）

0 引言

输电塔线体系由输电塔及基础部分、导线和地线、绝缘子、线路金具等组成。输电塔是塔线体系中主要承重结构，具有结构高、塔体结构柔度强、自重大以及较易在外荷载激励下产生显著振动等特点。风是引起输电塔振动的主要激励因素，沿海强台风地区风荷载是导致输电塔发生倒塌和事故的重要原因。输电塔主材杆件易在风荷载作用下产生振动疲劳导致输电塔倒塌［1］。2011 年7 月，南通地区受台风天气影响，两基直线塔发生倒塌，导致数十条线路发生断电，造成严重损失［2］。2012 年4 月，湖南某段输电线路受台风影响，发生三基直线塔倒塌、两基耐张塔损坏的事故［3］。2016 年4 号台风“妮妲”造成4基输电塔倒塌，致使该地区发生大面积停电，损失超过110 亿美元［4］。综上所述，台风是各个地区导致电力系统发生故障的主要原因之一。输电线路作为生命线工程结构，是保障人民基本日常生活、国家生产建设的基础。若发生输电塔风致倒塌会直接影响社会生产与生活秩序，带来严重损失。因此，为保障我国沿海强台风地区输电塔安全运行。需要合理地对该地区输电塔的抗风性能评估展开研究。

目前，采用易损性分析方法开展输电塔抗风性能评估较少，谢丽宇等［5］以塔顶最大位移角为评价指标对输电单塔进行易损性分析，评估输电塔抗风性能。王弘洋［6］采用动力增量法对输电塔进行易损性分析，绘制易损性曲线。但现有抗风性能评估大多仅针对单塔进行分析，忽略了塔线耦合效应的影响。

首先通过ANSYS 软件建立温州洞头3572 线新建的单回路猫头塔及塔线体系有限元模型，通过模态分析获得动力特性参数理论值。随后采用谐波叠加法生成具有台风特性的脉动风荷载时程，对塔线体系进行风振响应分析。最后考虑塔线耦合效应，进行输电塔的易损性分析，对其抗风性能进行评估。

1 研究对象及数值计算模型

1.1 工程背景简介

以温州洞头35 kV 大洞3572 线路Y30—Y33 段塔线体系为研究对象。该线路位于温州市洞头区，途经小门岛、大门岛、青山岛和洞头本岛。此段塔线体系采用的是“耐—直—直—耐”的单回路塔架设方案，该段平断面图如图1 所示。Y30、Y33 塔选用3560 型终端耐张塔，N31、N32 塔选用ZMG32 猫头塔，两基塔塔腿及以上结构完全一致，呼称高为28.5 m，塔高为34.5 m，根开为6.11 m。Y30—Y33 段导线型号为JL/G1A-185/30，安全系数k为2.6；地线型号为JLB20A-50 铝包钢绞线，安全系数k为4.0。绝缘子型号为FXBW8 悬式绝缘子。

图1 Y30—Y33段平断面图Fig.1 Plan and section of segments Y30—Y33

1.2 塔线体系有限元模型

ZMG32 输电塔根开为6.11 m，呼称高为28.5 m，塔高为34.5 m。主材为Q345 型钢，角钢截面为140 mm×10 mm，125 mm×10 mm。斜材采用Q235 型钢，角钢截面主要为90 mm×7 mm，56 mm×5 mm，63 mm×5 mm，75 mm×6 mm 等；辅助材采用Q235钢，角钢截面主要为90 mm×7 mm，56 mm×5 mm，63 mm×5 mm，75 mm×6 mm，40 mm×5 mm，80 mm×5 mm 等。主材、斜材和辅助材的弹性模量E均为2.06×106N/mm2，质量密度ρ均为7850 kg/m3。线路导线和地线参数见表1。

表1 导线和地线参数Table 1 Parameters of conductor and ground wire

将输电塔的主材、斜材、辅助材杆件视为梁单元（Beam188）；将塔线体系中的导线和地线视为单拉直线型杆单元（Link10）。将塔线体系的绝缘子串视为杆单元（Link10）。建模时两基塔的水平档距、垂直档距及高差等参数与实际工程一致。在铁塔塔腿底部施加4 个固定约束，两侧导线和地线施加z向位移约束。模拟输电塔实际工作情况。模型共有2 类ANSYS 单元，5 种材料模型，976 个节点，3 126 个单元。建立的塔线体系模型如图2 所示。

图2 塔线体系有限元模型Fig.2 The finite element model of the tower line system

1.3 风场模拟及风荷载施加

对塔线体系进行风振响应分析，首先要正确模拟出塔线体系所处的风场，得到不同施加点的风速v，进而通过规范计算塔身所受到风荷载值的大小。自然界中的风一般包含有两种成分：平均风和脉动风［7］。塔线体系内任意位置（y，z）处，某一时刻t的风速值等于该位置处平均风速加上该位置处相应的脉动风速v（y，z，t），如式（1）所示。通过此式可求得塔线体系任意高度任意时刻的风速值。

1.3.1 平均风的生成

平均风是指在一定时间内，风速的大小、方向等参量不会随着时间发生改变的风。根据现有研究可知平均风的自振周期一般超过10 min，因其自振周期远远大于输电塔等高耸结构的自振周期，不会引起风致动力响应，分析时通常将平均风当作静力荷载［8］。采用达文波特通过大量现场测试数据所得到的平均指数风剖面计算平均风速值vˉ，如式（2）所示。

式中：α为地面粗糙度系数，本工程实际情况为沿海地区及海岛，属A 类地形，粗糙度系数α取值为0.12；为10 m 高度处的平均风速；h为计算高度。

1.3.2 脉动风的生成

脉动风是由于风不规律性所引起的，风速的大小随时间发生不规则变化，需要采用统计的方法来描述脉动风值。由于脉动风频率与输电塔等高耸结构自振频率值大小较为相近，易对此类型结构产生较大的动力作用，因此常将脉动风当作动力荷载进行研究［9］。

采用台风风谱石沅谱，通过谐波叠加法对脉动风进行模拟，与之相关的初始参数如下：基本风速=35 m/s；地貌类别为A 类，α取0.12；梯度风高度为300 m；模拟总时长为100 s，时间步长Δt=0.1 s。湍流度为0.18［10］。N31 塔塔顶位置风荷载施加点脉动风速时程及自功率谱图如图3 所示。从图3（b）可知，本文采用的模拟方法得到的脉动风风速时程与目标谱较为一致，说明本文选用的模拟方法正确可行。

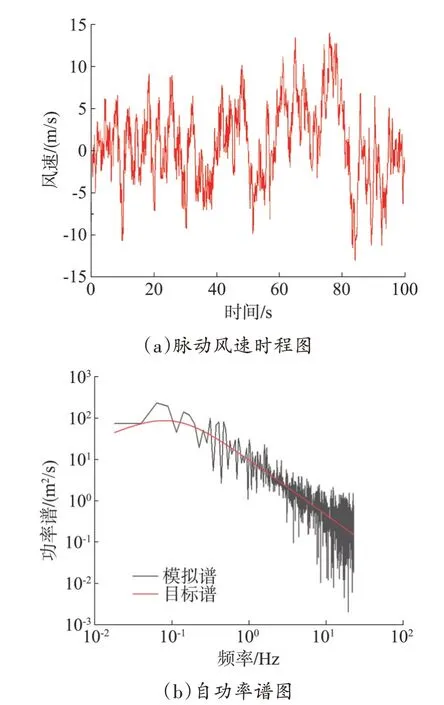
图3 脉动风速及功率谱Fig.3 Fluctuating wind speed and power spectrum

1.3.3 风荷载的施加

考虑所研究的塔线体系水平跨度较小，加载时忽略水平方向的风速不均匀性，仅考虑竖向剖面上的变化。具体加载时加载点及施加位置选择如图4 所示。

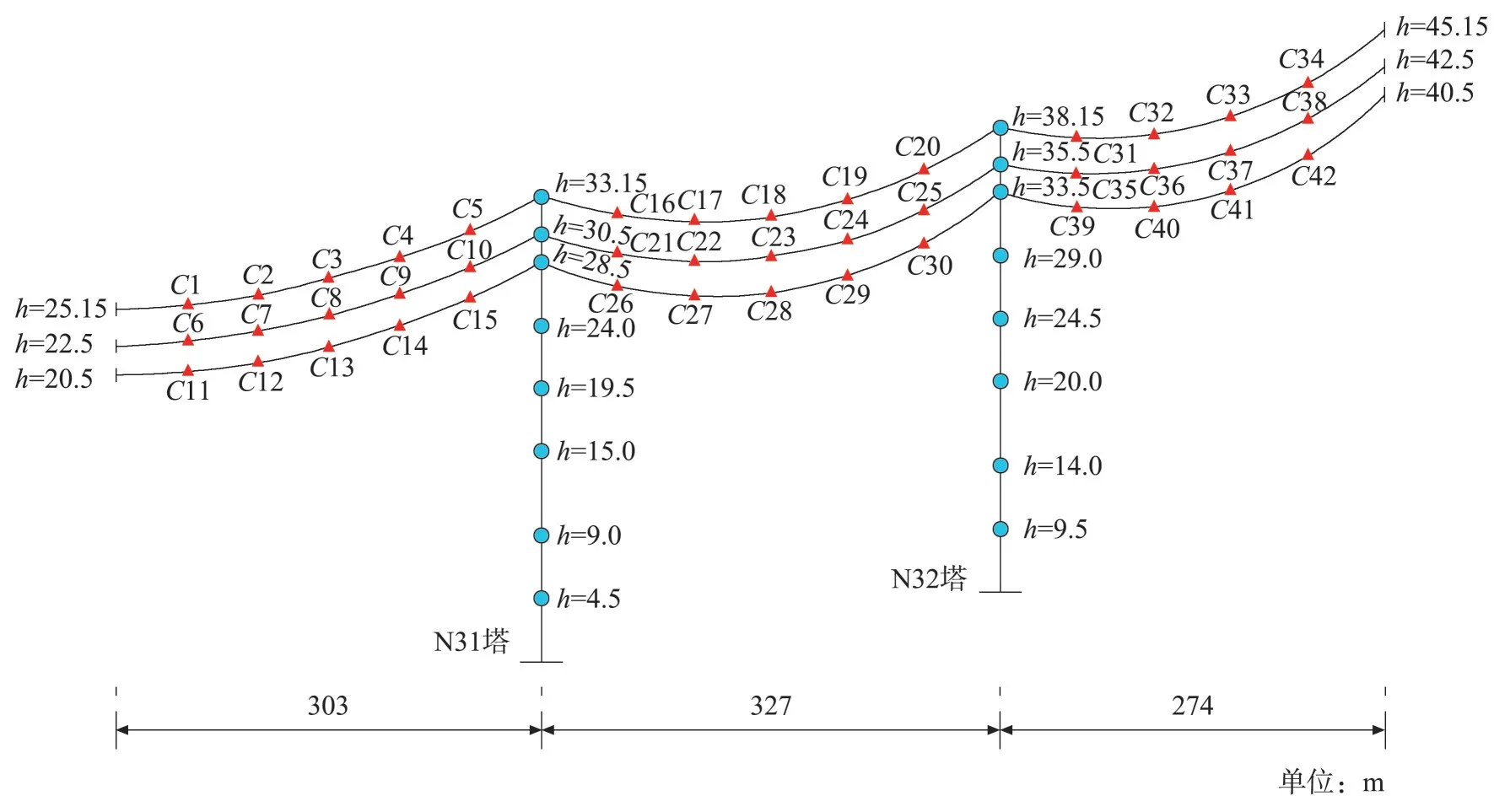
图4 塔线体系风荷载施加点示意图Fig.4 Schematic diagram of wind load application point of tower line system

2 塔线体系动力特性及风振响应分析

2.1 单塔及塔线体系动力特性分析

为更好地掌握输电塔及塔线体系振动特性，采用ANSYS 中的分块兰索斯法对单塔及塔线体系进行模态分析［11］，提取输电塔及塔线体系模态分析的频率及对应的振型。本文规定x向为输电塔顺线路方向；z向为输电塔横线路方向。单塔振型如图5 所示；塔线体系部分振型如图6 所示。

图5 单塔振型Fig.5 Single tower vibration mode

图6 塔线体系部分典型振型Fig.6 Typical vibration modes of tower line system

单塔和塔线体系前5 阶自振频率值，如表2 所示。

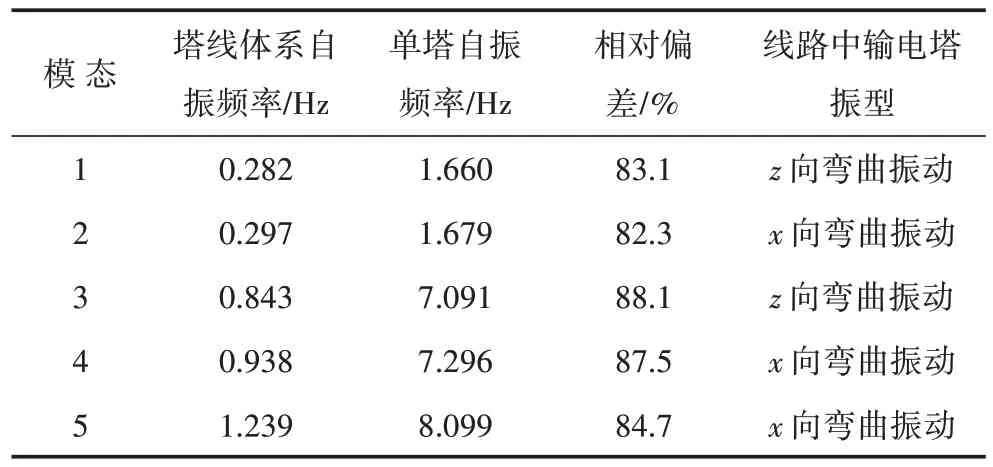
表2 单塔及塔线体系频率对比Table 2 Frequency comparison of tower and tower line system

通过单塔与塔线体系的模态分析可知，两者动力特性发生显著变化。塔线体系在低频区的振动显著、振动模态密集，主要以导线和地线振动模态为主。输电塔振型主要集中在高频区且往往不伴随导线和地线振型；塔线体系耦合使得塔线体系频率值显著降低；在脉动风荷载激励下可能产生较为剧烈的振动响应，因此应该将塔线体系作为整体进行分析。在输电杆塔设计中需要考虑导线和地线耦合作用对输电塔影响。

2.2 单塔及塔线体系风振响应

2.2.1 塔线体系风振响应分析（0°风）

图7 为0°风作用下，N31 塔与N32 塔塔顶位置处x向的位移时程；图8 为两塔各高度处的位移及应力均方根值对比图。

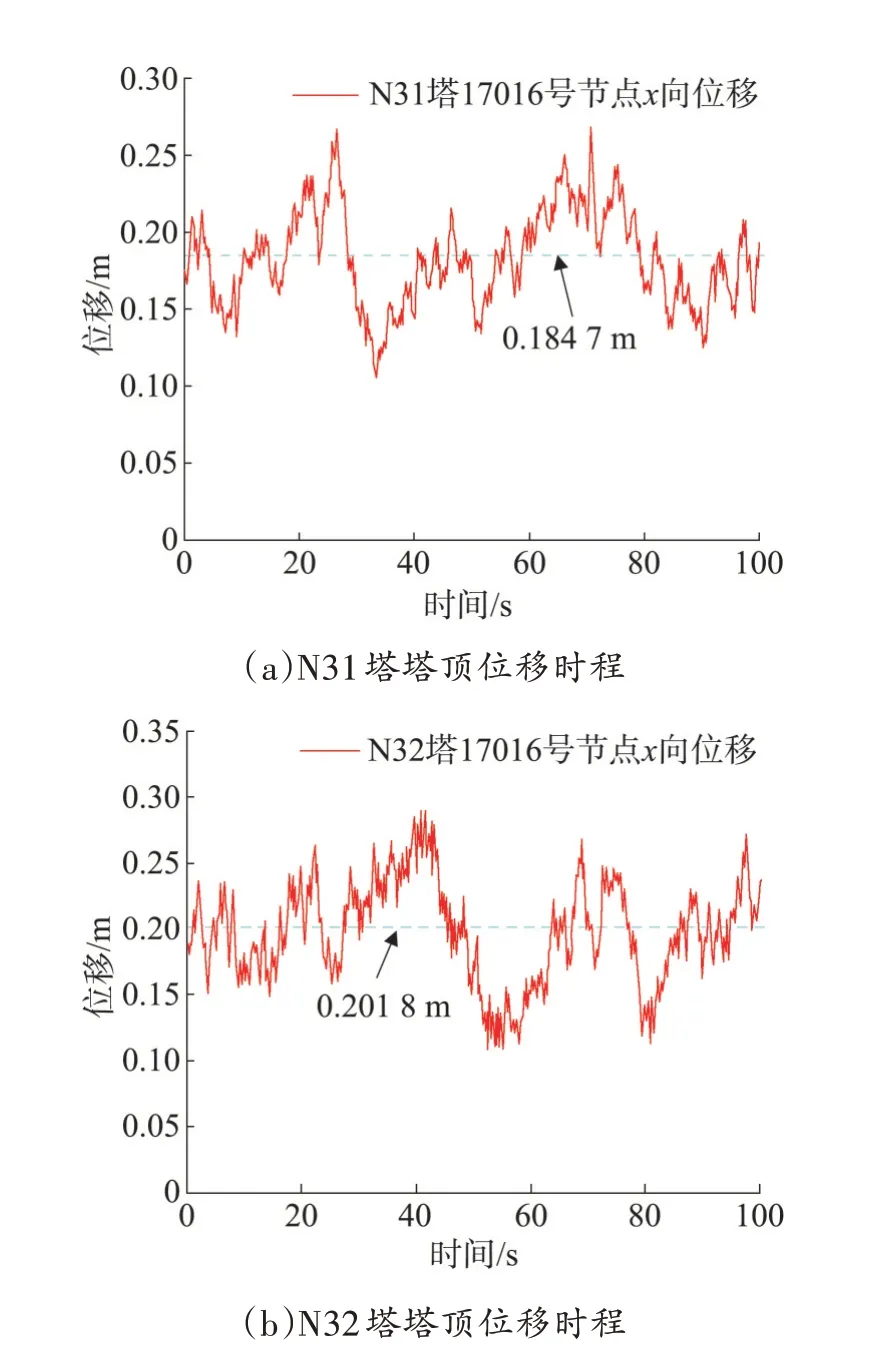
图7 塔顶位移时程曲线Fig.7 Time history plot of tower top displacement

图8 输电塔各层位移及应力均方根值Fig.8 RMS of displacement and stress of the transmission tower

由图7 可知，N31 塔塔顶位置位移均方根值为0.184 7 m。N32 塔塔顶位置位移均方根值为0.201 8 m，由于N32 塔所在位置高于N31 塔，塔身、导线、地线及绝缘子所受到的风荷载相比N31 塔更大，因此N32 塔相较N31 塔位移增大了9.3%。

由图8 可知，N32 塔每层位移均方根值及主材应力均方根值均大于N31 塔。在风荷载作用下，由于受到导线和地线的影响，使得输电塔的非线性增强，横担及塔头位置处位移值较大；N32 塔各层主材节点应力均方根值大于N31 塔值，两基塔的应力均方根值均在第二段达到最大。在塔线体系风振响应中，塔身受到风荷载作用，发生侧移。因此迎风面主材轴向压应力小于背风面主材轴向压应力，同时输电塔第二段主材横截面变小，导致背风面第二段应力值达到最大，此段为输电塔风致倒塌危险位置。

2.2.2 塔线体系风振响应分析（90°风）

图9 为90°风作用下，N31 塔与N32 塔塔顶位置处x向的位移时程；图10 为两塔各高度处的位移及应力均方根值对比图。

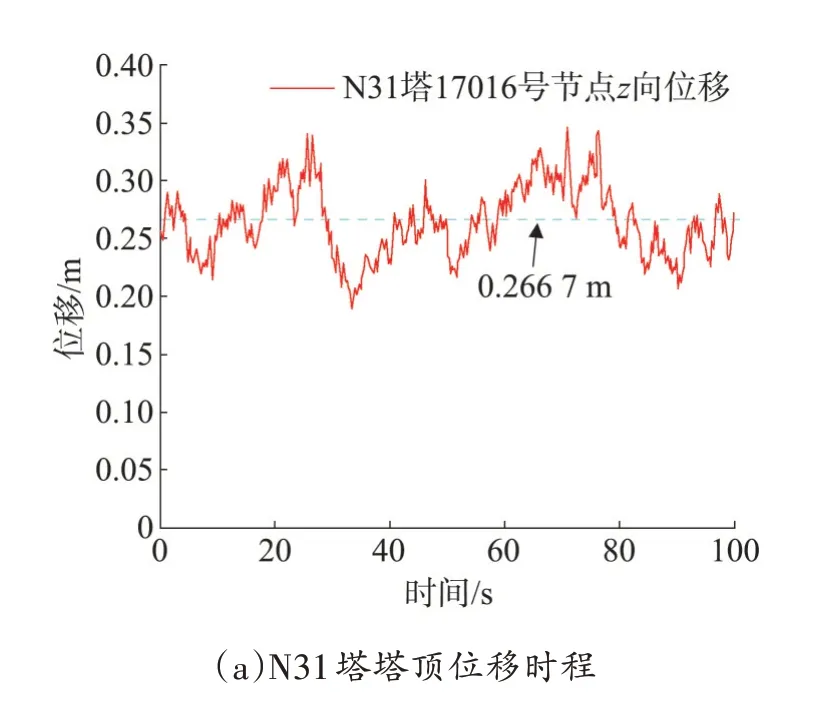
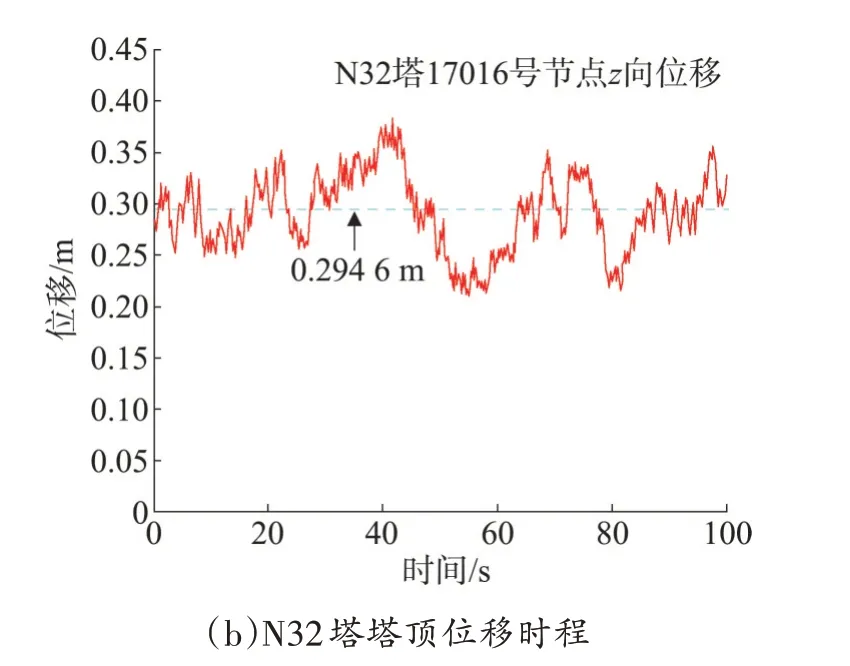
图9 塔顶位移时程曲线图Fig.9 Time history plot of tower top displacement

图10 输电塔各层位移及应力均方根值Fig.10 RMS of displacement and stress of the transmission

通过图9 和图10 可知：90°风向角风荷载作用下输电塔各高度处的z向位移均方根值均大于0°风向角工况各层位移均方根值；输电塔主材应力均方根最大值依旧位于第二段，较0°风向角输入时的应力均方根值较大，可见，90°风向角为铁塔倒塌破坏的最不利风向角。

3 考虑塔线耦合效应的输电塔易损性分析

3.1 输电塔抗风性能概率分析

3.1.1 破坏状态的定义

参考相关规范及输电塔破坏模式及失效规律研究［12］，可采用塔顶位移值作为指标确定输电塔的极限破坏状态，破坏状态划分及量化指标如表3 所示。表3 中，mDmi为轻微破坏状态界限值；mDma为中等破坏状态界限值；mDco为倒塌破坏界限值。

表3 输电塔结构破坏状态定义Table 3 Definition of the failure state of the transmission tower structure

3.1.2 输电塔极限状态量化指标概率分析

输电线路运行时会受到雨雪、腐蚀环境等因素影响，使得输电塔杆件密度、弹性模量以及屈服强度参数具有不确定性。选取杆件密度、弹性模量以及主材和辅材杆件屈服强度参数作为铁塔杆件的变量参数，通过拉丁超立方抽样方法［13］，生成80 组输电塔结构样本作为分析对象。杆件的初始材料参数基于输电塔设计理论值，选取标准差为均值的5%。采取倒三角分布侧向加载的方式，对80 组输电塔随机样本进行推覆（Pushover）分析，得到输电塔结构轻微破坏、中等破坏以及倒塌及严重破坏3 类极限状态所对应的位移均值及标准差值，对3 种破坏状态限值进行统计绘制直方图，如图11—图13 所示，指标的统计参数如表4 所示，βmi、βmd、βco分别为铁塔轻微破坏、严重破坏和倒塌破坏的位移标准差。

表4 输电塔极限状态指标统计参数Table 4 Statistical parameters of transmission tower limit state index

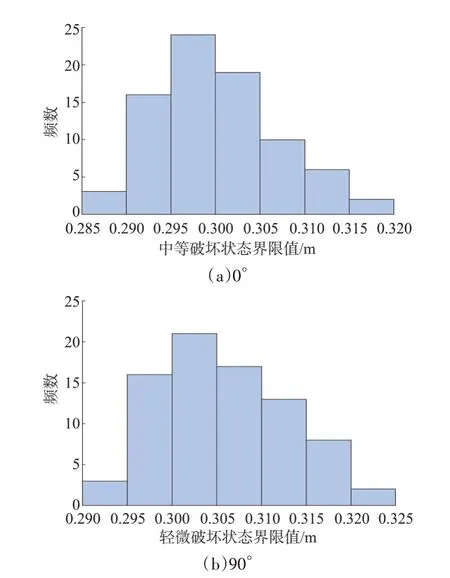
图11 输电塔轻微破坏样本频度统计Fig.11 Frequency statistics of samples with slight damage to transmission towers

图12 输电塔中等破坏样本频度统计Fig.12 Frequency statistics of medium damage samples in transmission towers

图13 输电塔倒塌破坏样本频度统计Fig.13 Frequency statistics of collapse and damage samples of transmission towers

由图11—图13 可知：轻微破坏及中等破坏界限值的分布规律明显，倒塌破坏界限值数据离散程度较大；当结构即将发生倒塌时，塔顶位移指标的不确定性较强，与实际情况较吻合；0°与90°风向角风荷载作用下3 种铁塔破坏状态抗力限值服从对数正态分布。

3.2 输电塔概率风荷载作用效应分析

采用前文的谐波叠加法，随机生成80 组台风风速样本，模拟风速范围为15～55 m/s，间隔0.5 m/s 取值，对80 组塔线体系随机样本施加0°及90°风向角的脉动风荷载，加载点同前文。受篇幅所限，不一一列举不同风速下80 组N32 塔随机样本的塔顶位移时程，仅将0°与90°风向角工况的80 组风速和N32塔塔头位移均方根值mD用对数坐标一一对应，得到如图14 所示位移均方根值与风速近似线性增长的曲线。对0°及90°风向角风荷载作用下结构响应数据进行回归分析，可得到风速响应趋势线方程如式（3）所示。

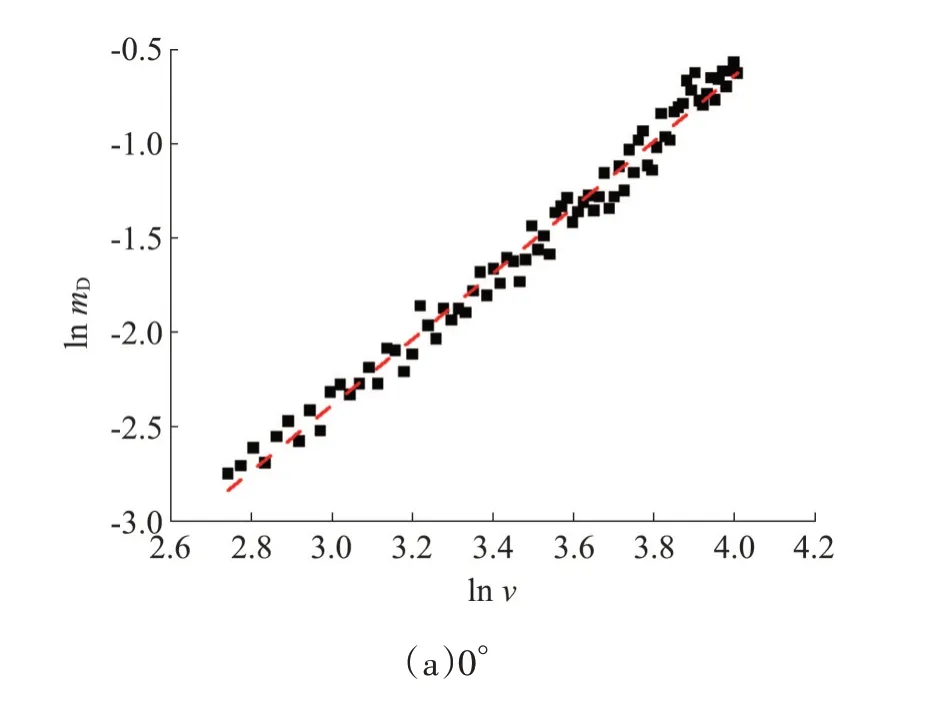
图14 N32塔塔顶位移回归曲线Fig.14 N32 tower top displacement regression curve

此外，进一步对0°及90°风输入下N32 塔顶位移响应进行了频次统计，得到0°及90°风N32 塔顶位移频度分布如图15 所示。由分布图可知，塔顶位移数据分布形态基本符合对数正态分布规律。

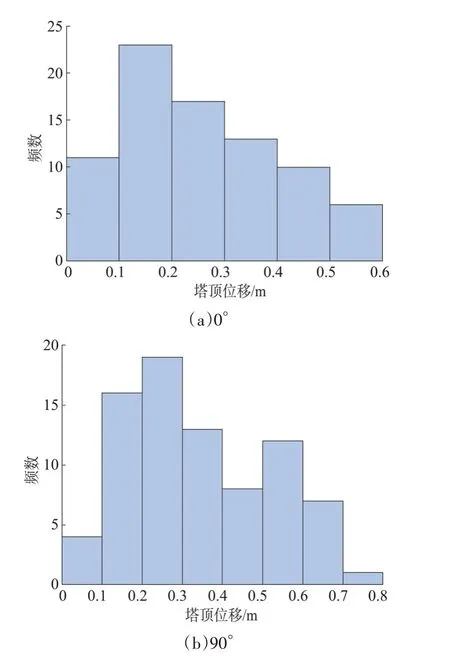
图15 N32塔塔顶位移频度统计Fig.15 N32 tower top displacement frequency statistical chart

基于以上统计数据可得到结构位移响应均方根的均值mˉD及其对数标准差值β，如表5 所示。

表5 N32塔顶位移响应统计参数Table 5 Statistical parameters of N32 tower top displacement response

3.3 输电塔风灾易损性分析

输电塔进行风灾易损性主要包括两方面的分析内容：一是通过动力增量法进行概率风荷载作用效应分析，拟合得到风荷载作用效应函数；二是通过开展猫头塔抗风能力概率分析，对输电塔随机样本进行Pushover 分析，确定输电塔在风荷载作用下极限状态对应的量化抗风能力指标限值［14］。风灾易损性曲线表示在不同大小的风荷载作用效应超过输电塔破坏阶段结构承载力的概率。风荷载作用效应Sd超过铁塔抗力Rc的失效概率Pf可按式（4）计算［15-17］。

式中：P（·）为概率函数。

根据前文可知，Rc和Sd都服从对数正态分布，所以特定阶段输电塔结构失效概率Pf为

式中：Φ为正态累计分布函数；为铁塔抗力均值；βc、βd分别为铁塔抗力和风荷载效应的标准差。

3.3.1 0°风向角工况的易损性曲线

根据上节分析结果，将塔顶位移与风速关系式（3）及各极限状态下结构承载力取值代入式（6），得到在0°风向角风荷载作用下塔线体系N32 输电塔各极限状态下失效概率公式，并绘制易损性曲线。

0°风向角风荷载作用下N32 塔轻微破坏失效概率公式为

0°风向角风荷载作用下N32 塔中等破坏失效概率公式为

0°风向角风荷载作用下N32 塔倒塌破坏失效概率公式为

通过式（6）—式（8）计算得到风速与结构处于不同极限状态下的失效概率的关系，如图16 所示。

图16 0°风向角工况N32塔风灾易损性曲线Fig.16 Wind vulnerability curve of N32 tower under 0°wind angle condition

由图16 可知：在0°风向角风荷载作用下，随着风速的增加，N32 塔达到各极限状态的概率值也随之增大。在遭受重现期30 年风速（28.28 m/s）时，N32塔发生轻微破坏阶段概率为71.52%，中等破坏概率为29.75%，但发生倒塌破坏概率为2.18%。在遭受重现期50 年风速（35.77 m/s）时，N32 塔发生轻微破坏阶段概率为88.47%，中等破坏概率为50.07%，发生倒塌破坏概率为6.63%。在遭受重现期100 年风速（41.95 m/s）时，N32 塔发生轻微破坏阶段概率为96.35%，中等破坏概率为65.50%，但发生倒塌破坏概率为12.71%。当极值风速达到47.5 m/s，N32 塔发生轻微倒塌概率为100%，此时中等破坏概率为74.90%，倒塌概率为19.09%。当极值风速达到55 m/s，N32 塔发生中等破坏概率达到82.80%，倒塌概率为28.85%。

3.3.2 90°风向角工况的易损性曲线

同上，可得到90°风向角风荷载作用下N32 塔轻微破坏失效概率公式为

90°风向角风荷载作用下N32 塔中等破坏失效概率公式为

90°风向角风荷载作用下N32 塔倒塌破坏失效概率公式为

通过式（9）—式（11）计算得到风速与结构处于不同极限状态下的失效概率的关系，如图17 所示。

图17 90°风向角工况N32塔风灾易损性曲线Fig.17 Wind vulnerability curve of N32 tower under 90°wind angle condition

由图17 可知：90°风向角下易损性曲线与0°风向角下易损性曲线较为类似，在90°风向角风荷载作用下，随着风速的增加，N32 塔达到各极限状态的概率值增大。在遭受重现期30 年风速（28.28 m/s）时，N32 塔发生轻微破坏阶段概率为81.39%，中等破坏概率为45.98%，但发生倒塌破坏概率为2.79%。在遭受重现期50 年风速（35.77 m/s）时，N32 塔发生轻微破坏阶段概率为94.54%，中等破坏概率为65.50%，发生倒塌破坏概率为13.24%。在遭受重现期100 年风速（41.95 m/s）时，N32 塔发生轻微破坏阶段概率为100%，中等破坏概率为77.17%，发生倒塌破坏概率为20.19%。当极值风速达到55 m/s，N32塔发生中等破坏概率达到93.59%，倒塌概率为37.10%。在相同风速下，发生破坏概率相较0°风向角略高，与分析结果相符。综上所述，塔线体系中N32 塔在90°风向角强台风作用下抗风性能较好，但在强台风作用下也有发生倒塌的概率。在相同风速下，发生破坏概率相较0°风向角略高，在抗风设计中应引起注意。

4 结论

采用ANSYS 有限元软件建立符合实际工程的单塔和两塔三线有限元模型，进行模态分析；采用谐波叠加法模拟生成施加点的脉动风时程，研究不同风向角工况塔线体系的风振响应特点；最后考虑结构和风荷载的不确定性，对拉丁抽样方法生成的大量随机样本进行风荷载作用效应分析和Pushover 分析。基于上述分析结果，进行了考虑塔线耦合效应的输电塔风灾易损性分析，对输电塔的抗风性能进行评估。主要得到以下结论：

1）随着风向角的增加，塔线体系所受风荷载值增大，导致在同一风速作用下结构发生破坏的概率值增大。v10=55m/s 极限风速作用下，90°风向角工况发生中等破坏和倒塌破坏的概率较0°风向角工况增加了10.8%和8.2%。

2）在90°风向角工况，在遭受30 年重现期风速（v10=28.28 m/s）时，N32 塔以基本完好为主，部分发生轻微破坏，发生倒塌破坏的概率2.79%；在遭受50 年重现期风速（v10=35.77m/s）时，发生倒塌破坏的概率为13.24%；在遭受100 年重现期风速（v10=41.95 m/s）时，发生倒塌破坏的概率为20.19%。在遭受55 m/s 极值风速时，发生倒塌破坏的概率为37.1%。