海岛大跨越输电塔线体系风振响应及动力失稳分析

于佳宝，卓 越，张佳毅，郑 翀，曹枚根

（1.北方工业大学，北京 100144；2.四川电力设计咨询有限责任公司，四川 成都 610016；3.国网浙江省电力有限公司温州供电公司，浙江 温州 325000）

0 引言

近年来，随着海洋经济迅速发展，大陆与岛屿间能源输送需求愈发强烈。海岛地区地形复杂，面积狭小且四面环海，与大陆连接方式受限，跨海输电线路已经成为连接大陆和岛屿的能源输送的重要手段之一。跨海输电线路具有铁塔高、跨度大和恢复困难等特点，且常年处于大风量、高风速的运行环境中，风振响应特点较常规线路存在较大差异。强风作用下，输电线路倒塌事故时有发生［1-3］。开展输电塔线体系风振响应特点及强风作用下的倒塌破坏研究，对提高输电塔抗风性能和指导输电塔抗风加固设计具有重要意义。

风振系数是大跨越输电塔风荷载重要计算参数，现行风振系数规范将输电塔和导线、地线分开考虑。李正良等［4］通过风洞试验和数值模拟的方法研究了输电塔考虑导线、地线耦合作用下的风振响应规律并计算对应的风振系数，研究表明输电塔横担处风振系数会发生突变。汪大海等［5］基于风洞试验对比研究了单塔及塔线体系的风振响应变化规律。付兴等［6］基于惯性力法获得风振系数，揭示了塔线耦联效应的影响。丁祥等［7］开展了不同地基不均匀沉降程度对输电塔抗风性能的影响研究，发现地基沉降所造成的结构倾斜，会导致风振系数超过规范值，风振系数随着倾斜角度的增大而增大。Meng 等［8］研究了输电塔线体系在不同风速和风向下的风振响应，阐述了风速对输电塔线耦合效应的影响。王文明等［9］对不同风向角下的输电塔线体系进行风洞试验研究，发现0°～30°塔线体系因输电线在顺线路上的阻尼作用，降低了其风振响应。朱云祥等［10］基于频域分析方法对输电裸塔及塔线体系开展了带有脉动风载效应的功率谱分析，发现由于导线和地线的存在，塔线体系在横向风荷载作用下，其在低频区能量显著高于裸塔。

此外，为减少风致输电塔倒塌事故，国内外研究学者通过风洞试验和数值模拟等方式对其倒塌机理展开研究。Asgarian 等［11］提出了容量需求比，用以识别关键构件，并采用Pushdown 分析确定了结构的剰余承载力。李悦等［12］利用参数共振理论推导了输电塔杆件的动力失稳区和激发系数表达式，并通过风洞试验进行验证。吉柏锋［13］建立了角钢输电塔主材失稳的弯矩-轴力-轴向刚度关系曲面，并基于此开展下击暴流作用下输电塔线体系动力失稳特点分析。魏文晖等［14］基于能量法开展了输电塔线体系在下击暴流作用下的弹塑性动力稳定性分析，结果表明能量法能快速准确地确定输电塔线体系整体失稳时刻。毕文哲等［15］研究了输电塔在下击暴流作用下的倒塌机理，研究表明关键构件的屈曲是引起输电塔发生渐进式倒塌的主要原因。

综上，已有相关研究在大跨越导线和地线对输电塔风振响应的影响效果结论上存在差异，海岛大跨越输电塔线体系的风振响应及动力稳定性相关研究仍然欠缺。因此采用ABAQUS 软件建立跨海段两塔三线有限元分析模型，通过研究其动力特性以及风振响应来揭示典型塔型在风荷载作用下的风振响应特点及塔线耦合效应，随后开展强风作用下塔线体系的倒塌破坏分析，对塔线体系的薄弱环节及破坏特点进行了详细阐述。

1 研究对象及风荷载模拟

1.1 线路概况

以温州洞头35 kV 某线路典型跨海段（耐—直—直—耐）线路为研究对象。该线路总长为1 367 m，其中直线塔间跨海段档距为1 196 m，两侧分别为87 m和84 m。直线塔G23、G24 选用2B10 型猫头型跨越塔，且两直线塔除塔腿高度相差1 m 外，塔身和塔头参数完全一致。其中G23 输电塔呼高47 m，总高56.5 m，铁塔根开10.25 m。G24 输电塔呼高46 m，总高55.5 m，铁塔根开9.98 m。线路平断如图1 所示。输电塔主材在塔身中部横隔面以上选用Q345，横隔面以下选用Q420，斜材选用Q345 和Q235 等边角钢制成。

图1 跨海段输电线路平断面图Fig.1 Cross sea transmission line cross-section diagram

线路中导线选用JLHA1/G1A-240/40 型钢芯铝合金导线，安全系数k=2.75。地线选用OPGW-90-24B1光纤复合，安全系数k取3.5。导线和地线参数见表1。

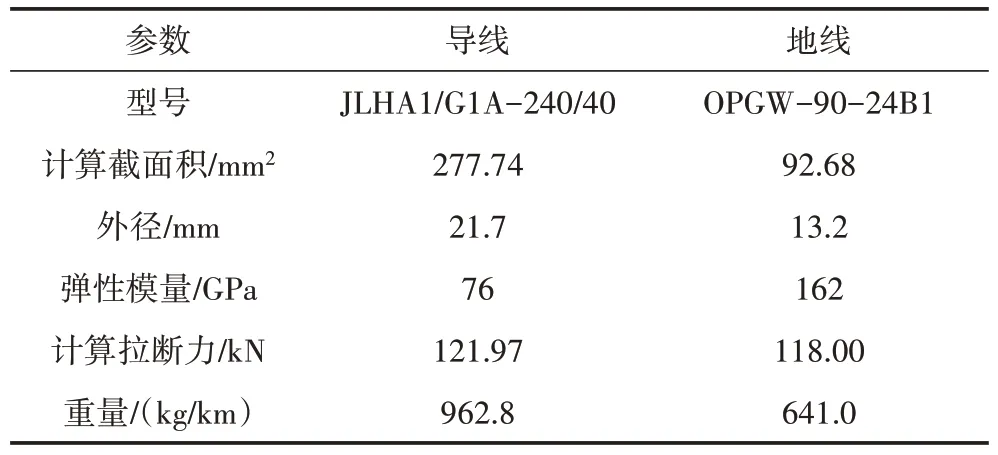
表1 导线、地线设计参数Table1 Design parameters of conductor and ground wire

1.2 塔线体系有限元模型

依据线路实际工程信息，基于ABAQUS 建立“两塔三线”有限元模型。角钢构件采用理想弹塑性双折线本构模型，材料阻尼比取0.02。输电塔用梁单元B31 进行模拟，导线和地线基于悬链线理论选用T3D2 单元进行找形模拟。计算裸塔时，考虑导线、地线质量效应，将导线、地线简化为等效质量增加至塔头导线、地线挂点处。图2 为塔线体系有限元模型。假定顺线路方向（z向）为0°风向角，横线路方向（x向）为90°风向角。

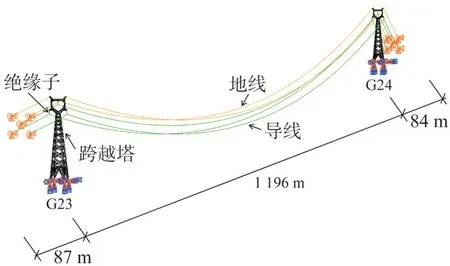
图2 塔线体系有限元模型Fig.2 Finite element model of tower line system

1.3 风荷载模拟

t时任意高度h处的风速V()h,t可视为平均风速和脉动风Vd(h,t)的叠加［16］，即

平均风与高度变化之间的规律用指数律来描述，即

式中：m为梯度风高度变化系数，取1.284；A 类地貌下风剖面指数α取0.12。

选用Davenport 谱作为目标功率谱来模拟脉动风时程，其表达式为：

式中：Sv(n)为风速谱；n为脉动风频率；kw为地面粗糙度的系数。

基于MATLAB 建立满足Davenport 谱的风速时程，G24 输电塔塔顶代表点处的脉动风速时程及其功率谱如图3 所示。

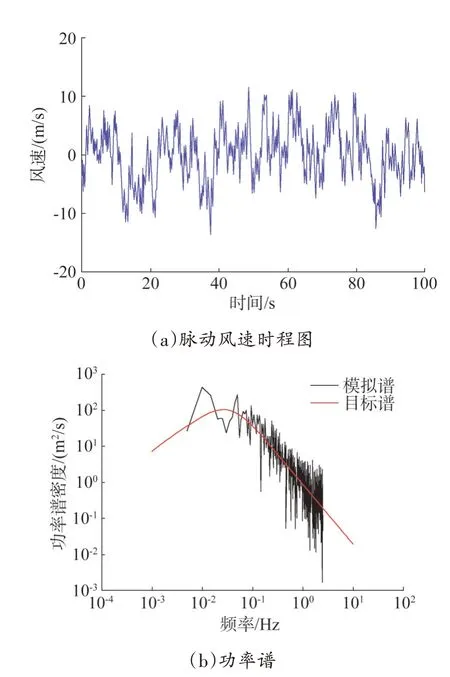
图3 塔顶脉动风速时程及功率谱图Fig.3 Time history and power spectrum of fluctuating wind speed at the top of the tower

在得到风速时程之后，按照相关规范［17-18］，将风荷载施加至等效加载点上，塔线体系风荷载施加点如图4。输电塔和导线、地线某一高度处风荷载时程计算如式（5）和式（6）所示。

图4 风荷载加载点示意图Fig.4 Schematic diagram of loading points of wind load simulation

式中：Ft(h,t)、Fx(h,t)分别为t时输电塔、导线和地线在高度h处风荷载；μs、μsc分别为输电塔、导线和地线的体型系数；As为迎风面构件的净投影面积；d为导线或地线的外径。

2 模态分析

为分析悬挂导线和地线对猫头塔动力特性的影响，采用Lanczos 法分别求解输电线、裸塔和塔线体系中G24 塔的动力特性参数和振型。

2.1 输电线动力特性

以一条导线为例对其进行模态分析以获取其振动模态及动力特性参数，导线振型如图5 所示，为清晰表现导线振型，图中将未变形导线画为黑色，蓝色表示该阶振型。

图5 导线振型Fig.5 Vibration modes of conductor

2.2 裸塔动力特性

图6 给出了裸塔的前3 阶振型，由振型结果可知，G24 输电塔的主要振型为z向1 阶振动、x向1 阶振动和整体1 阶扭转振动。其频率分别为1.513 9 Hz、1.519 2 Hz 和2.989 8 Hz。可以看出，顺线路与横线路方向自振频率非常接近，原因在于该跨越塔结构较为对称，仅在塔头处质量和刚度稍有变化。

图6 裸塔振型Fig.6 Vibration modes of the transmission tower

2.3 输电塔线耦合的动力特性

由模态结果可知，塔线体系的振型具有低频率、高密度的特点，塔线体系前297 阶皆为导线或地线振型，这与导线、地线这类柔索结构的受力特点及材料特性密不可分。导线z向1 阶振动频率仅为0.061 2 Hz、x向1 阶振动频率为0.120 9 Hz；地线z向1 阶振动频率为0.07 Hz、x向1 阶振动频率为0.138 4 Hz。与裸塔同振型频率相对比，以跨越塔为主要振型的自振频率较裸塔有所增大，这是因为柔索结构具有一定的刚度，使得输电线不仅增加了输电塔线体系的重量，还提供了一定的刚度贡献［19］。塔线体系中输电塔的主要振型如图7 所示。

图7 输电塔线体系振型Fig.7 Vibration modes of the transmission tower-line system

3 风振响应分析

3.1 0°风向角下的风振响应分析

在设计风速为41 m/s 且风向角为0°下，裸塔及塔线体系中G24 塔顶处位移均方根值分别为0.303 m 和0.233 2 m。塔线体系风振响应较裸塔有所降低，这是由于大跨越段水平和垂直档距较大且输电线在顺线路方向的阻尼作用，降低了塔线体系的风振响应。塔线体系和裸塔塔顶位移时程曲线如图8（a）所示。

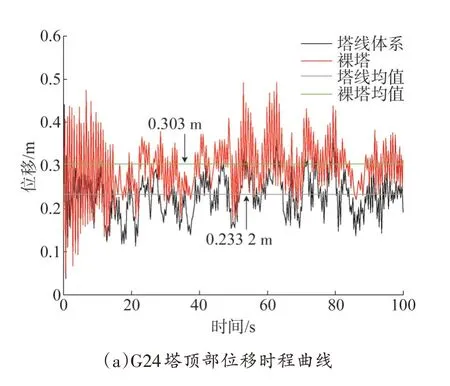
图8 0°风向角下G24塔顶部位移响应及其功率谱Fig.8 Top displacement response and power spectrum of G24 tower at 0°wind direction

脉动风的响应可分为背景响应和共振响应两部分［20］。图8（b）为裸塔及塔线体系顶部位移功率谱。从图中可以看出，裸塔及塔线体系均在低频率部分存在较高能量分布，此部分为结构响应功率谱与脉动风自功率谱形状相同的背景响应部分。其次，在共振响应部分，裸塔的共振响应卓越频率为1.48 Hz，该频率对应输电塔z向1 阶振动频率；塔线体系的卓越频率为0.11 Hz、0.14 Hz、1.56 Hz，其分别对应导线、地线z向1 阶振动频率和输电塔z向1阶振动频率。

由图9 可知，0°风向角下输电裸塔G24 的位移及主材应力响应均大于输电塔线体系，这也体现输电线的存在增大了输电塔在顺线路方向振动的阻尼效应。输电塔位移响应在塔身第5 节间（层高23.2 m）之后，层间位移差逐渐增大。同时裸塔及塔线体系主材应力均方根值均在塔身第5 节间处（层高23.2 m）达到最大。

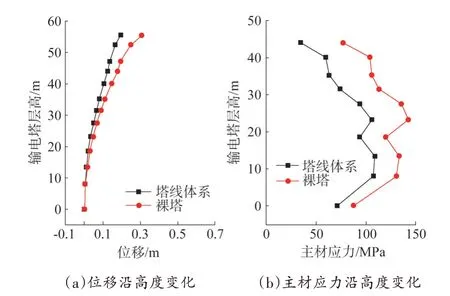
图9 G24塔位移及应力响应Fig.9 RMS of displacement and stress response of G24 tower

3.2 90°风向角下的风振响应分析

由图10 所示，在设计风速41 m/s 且风向角为90°下，裸塔及塔线体系中G24 塔顶处位移均方根值分别为0.405 1 m 和0.657 5 m。塔线体系塔顶位移响应均方根值较裸塔增大到1.62 倍。这是因为导线、地线的存在加大了迎风面积且导线、地线由于端部的张力差带动输电塔耦合振动。塔线体系和裸塔塔顶位移时程曲线如图10（a）所示。

图10 90°风向角下G24塔顶部位移响应及其功率谱Fig.10 Top displacement response and power spectrum of G24 tower at 90°wind direction

在塔线体系及裸塔位移功率谱图中可以看出，90°风向角下，塔线体系的背景响应远大于裸塔，这说明导线、地线的存在增强了输电塔的背景响应部分。在共振响应部分，裸塔的共振响应卓越频率为1.49 Hz，此频率对应输电塔x方向1 阶振动频率。塔线体系中G24 塔的卓越频率为0.06 Hz、0.08 Hz 和1.65 Hz，分别对应导线、地线1 阶平面外振动频率和输电塔1 阶平面外振动频率。裸塔及塔线体系顶部位移功率谱如图10（b）所示。

90°风向角下裸塔及塔线体系中G24 塔各高度处的位移、主材应力响应如图11 所示。由图可知，90°风向角下塔线体系中G24 塔各层位移及主材应力响应均大于裸塔。由于塔线耦合效应，使得塔线体系主材应力响应较裸塔增加到1.3 倍，但未改变输电塔主材应力分布。

图11 G24塔位移及主材应力响应Fig.11 G24 tower displacement and main material stress response

3.3 输电线对输电塔风振响应影响分析

为更清晰认识输电塔线之间的耦合效应，通过大跨越段的导线和地线中点位移及导线和地线与塔连接处的动张力差来描述输电线对输电塔的影响程度。其中动张力差可视为输电线在绝缘子连接处对输电塔施加的动态载荷［19］。

不同风向角下大跨越段导线、地线中点位移时程如图12 所示，对比0°及90°风向角下导线、地线顺风向位移均方根值可知，虽然受导线和地线耦合效应影响，杆塔结构在横、顺线向阻尼效应均有增大，但在输电线迎风面积较大的90°风向角下，输电线在风荷载作用下产生较大面外位移，使得塔线体系在横线向耦合响应更加显著。

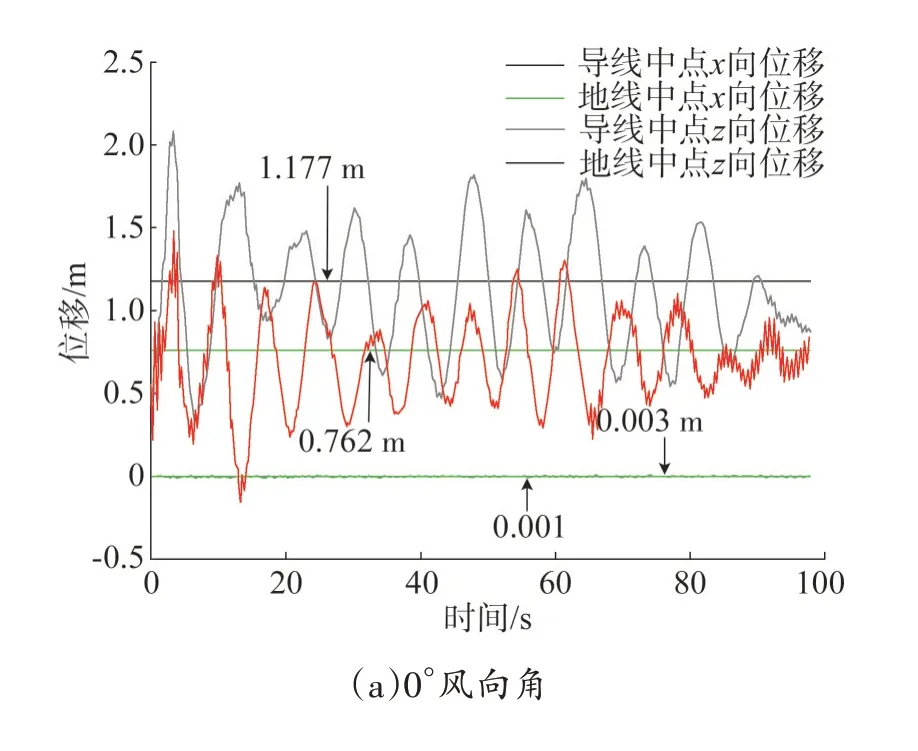
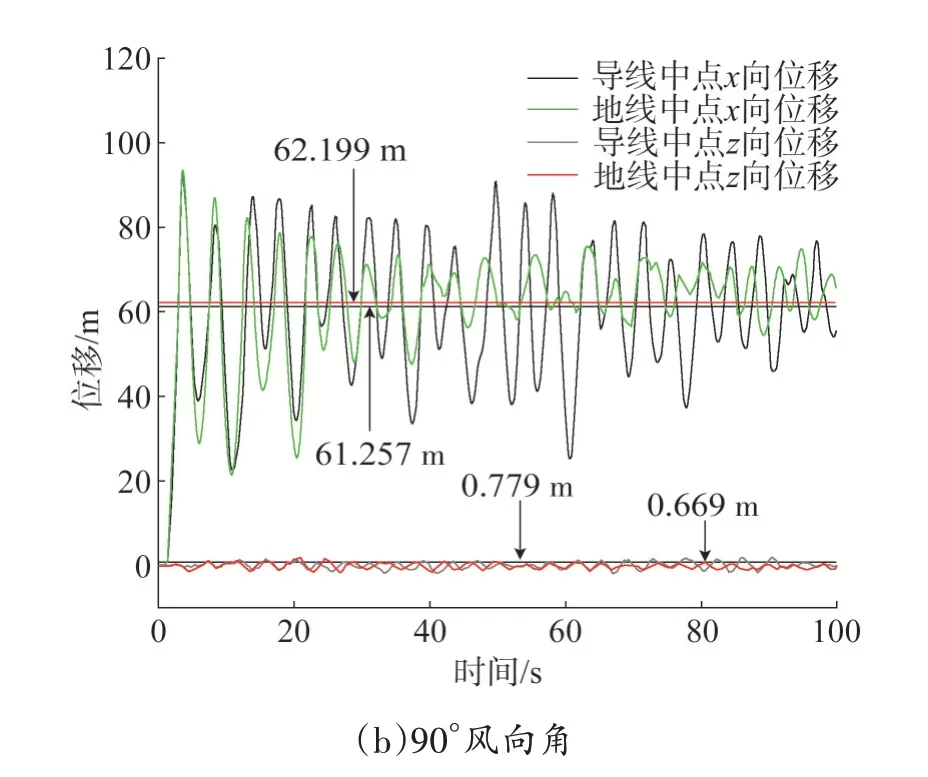
图12 不同风向角下导线、地线中点位移时程Fig.12 Time course of the displacement of the midpoint of the conductor and ground under different wind angles

图13 为不同风向角下导线、地线挂点两侧动张力差时程，其中地线挂点两端的动张力差显著大于导线，在0°及90°风荷载作用下其极值分别达到17.6 kN 和38.3 kN。90°风荷载作用下塔线体系虽在顺线路方向未施加荷载，但由于导线和地线在横向风作用下引起较大面外位移，致使输电塔在顺线路上也受到较大动态荷载作用，从而增加了结构的风振响应。

图13 不同风向角下导线、地线挂点两侧动张力差时程Fig.13 Time course of dynamic tension difference between the two sides of the wire and ground point under different wind angles

3.4 风振系数

风振系数是输电塔风荷载重要计算参数，其常用来考虑风荷载脉动部分对结构风振响应的影响。根据前文塔线体系风振响应分析计算结果，可通过式（7）计算各工况下杆塔各高度处的位移风振系数。

式中：Dmean为结构位移的平均值；σ为结构位移的均方差值；g为峰值因子，取2.5。

DL/T 5485—2013《110～750 kV 架空输电线路大跨越设计技术规定》中规定：对不超过60 m 的杆塔，风振系数对全高采用同一系数［19］。G24 输电塔全高为55.5 m，规范查表确定风荷载调整系数为1.555。将各工况下杆塔的位移风振系数计算值与规范中考虑脉动风的杆塔风荷载调整系数对比。G24 塔位移风振系数与规范值对比情况如图14所示。

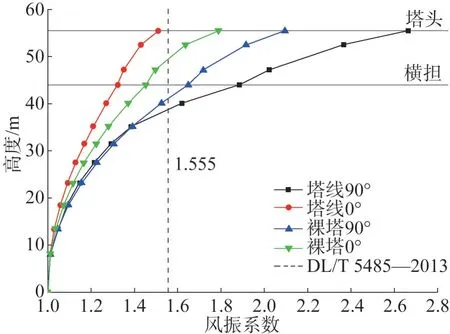
图14 G24塔位移风振系数Fig.14 Wind induced vibration coefficient of displacement of G24 tower

从图14 可以看出，裸塔及塔线体系的位移风振系数计算值在横担处均出现突变且均超过规范值。各工况下最大风振系数取自90°风向角工况塔线体系G24 输电塔塔顶处，其值为2.66。因此在对输电塔风荷载计算及风振系数取值时，要考虑横担处风振系数突变的影响和输电线对杆塔风振系数的影响。

4 强风作用下输电塔线体系动力倒塌分析

4.1 倒塌准则及极限风速确定

以输电塔由风荷载作用引起塔顶位移作为衡量输电塔破坏程度的量化指标。倒塌准则定义为：输电塔塔顶位移较前一稳定态出现大幅发散、突变等变化时，认为输电塔完全倒塌［21］。

利用增量动力分析方法对大跨越输电塔线体系在90°风向角风载下的动力非线性稳定进行研究。由图15 可知，当平均风速达到35 m/s 时，塔线体系中G24 输电塔位移响应最大值为0.531 m，结构进入轻微损伤状态；平均风速达到40 m/s 时，塔顶位移响应最大值达到0.842 m，此时输电塔进入损伤状态；当平均风速由44 m/s 增至46 m/s 时，塔顶位移急剧增加，结构位移响应最大值为18.2 m，结构发生倒塌破坏。

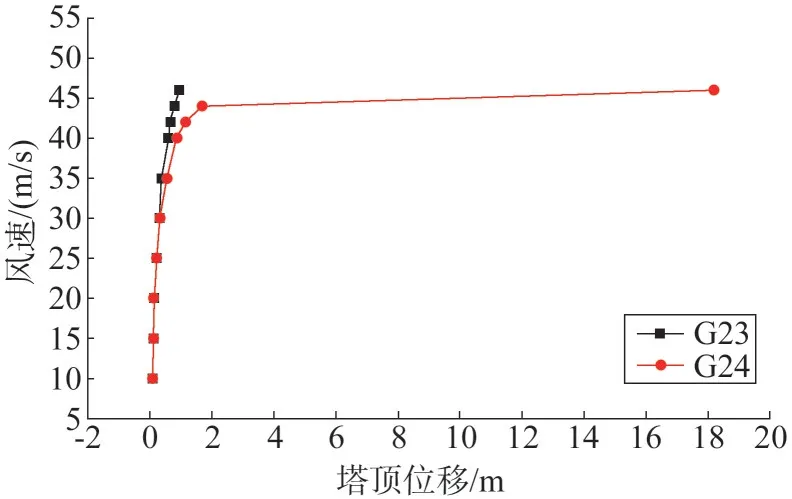
图15 塔线体系风速-塔顶位移关系曲线Fig.15 Wind speed-top displacement relationships for transmission tower line systems

4.2 塔线体系倒塌过程分析

在90°风向角下，当风速达到46 m/s 时，塔线体系中G24 跨越塔发生风致动力倒塌破坏。图16 为塔线体系塔顶水平位移时程曲线。G24 输电塔在49.9 s 时完全倒塌，而G23 输电塔塔顶位移稳定，未出现发散现象。

图16 塔线体系塔顶位移时程曲线Fig.16 Time-history curves of the tip displacement of the transmission tower-line system

大跨越输电塔线体系的风致倒塌过程如图17所示，图中红色标记杆件为失效杆件。t=48.3 s 时，第8 节、第9 节间斜材（杆件编号E1889 和E1790）首先发生失效，引起其周围杆件内力重分布。因此在48.3 s 之后，塔顶位移迅速发展，结构开始产生变形。当t=48.8 s 时，内力向下传递至第6 节、第7 节间，引起多根杆件发生破坏，相邻杆件迅速失效，输电塔塔体变形明显。当t=49.4 s 时，塔身中部大量杆件失效，塔顶水平位移进一步增大；当t=49.9 s 时，输电塔塔身中上部弯折，输电塔完全倒塌。从出现杆件失效至输电塔完全倒塌，历时1.6 s。

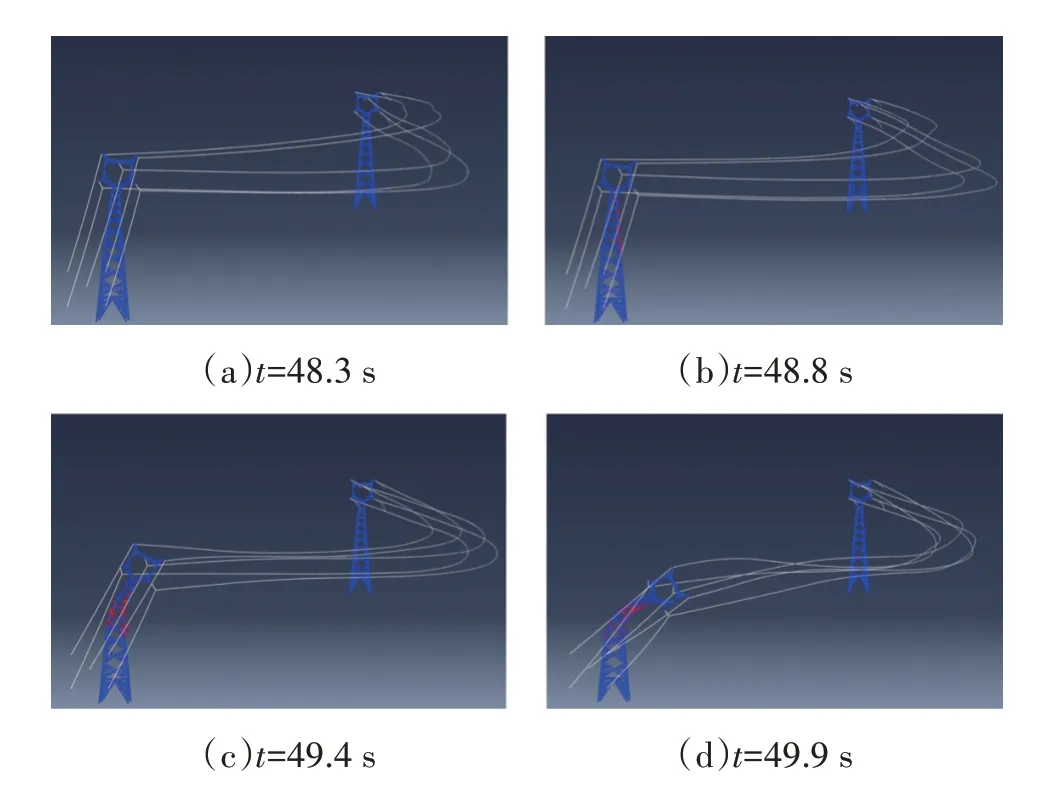
图17 特定时刻塔线体系输电塔变形图Fig.17 Deformation diagram of transmission towers in tower line system at specific times

图18 为首先失效杆件E1790 的轴向应力-杆件面外变形时程曲线，在图中能清晰看出，在2.9 s 时，构件开始产生面外变形，但程度较小。在48.3 s 时杆件面外变形进一步增加并发生跳跃型失稳，以致杆件丧失承载能力，引起输电塔内力重分布，进而引起输电塔失效倒塌。

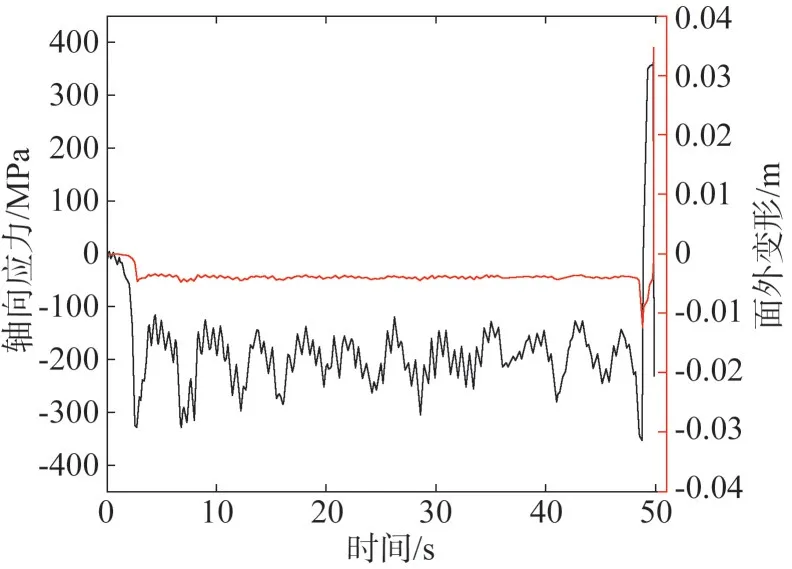
图18 杆件E 1790的轴向应力及杆件面外变形时程图Fig.18 Axial force and lateral deformation time-history curve of element E 1790

出现失效杆件前后塔身主材轴向应变峰值沿节间段分布如图19 所示，可以看出，在杆件出现失效后，主要影响区域为第5—第8 节间段，对应为塔身中上部，且影响程度最为严重的是第5 和第8 节间段，在图中也能看出，杆件失效后，结构内力重新分布且逐渐向下传递，引起大面积杆件失稳，最终导致输电塔发生倒塌。

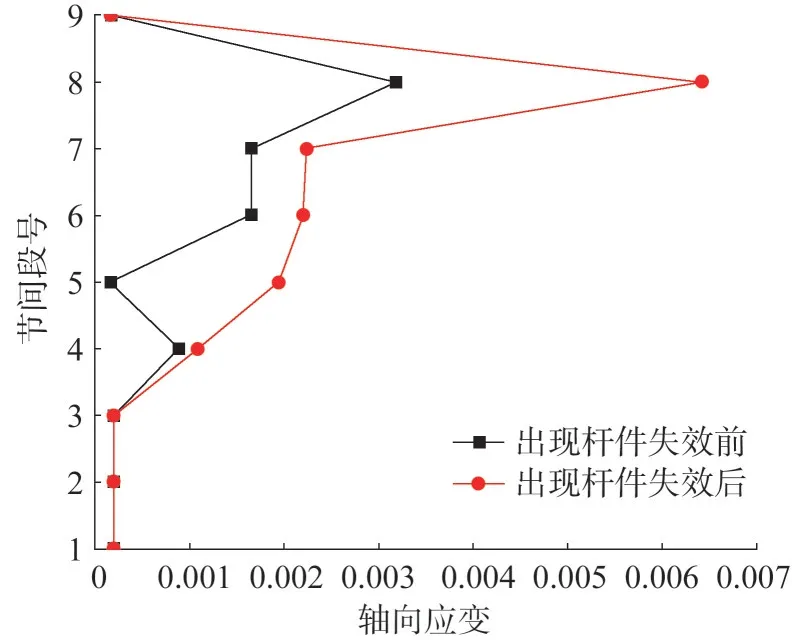
图19 塔身主材轴向应变峰值沿高度分布图Fig.19 Peak axial strain along the height of the tower’s main bracings

5 结论

1）塔线耦合效应在脉动风作用下表现复杂，在0°风向角下（顺线路方向）输电线的存在增大了体系的阻尼，抑制了塔线体系的风振响应，而在90°风向角下（横线路方向）输电线面外振动明显且两侧档距差异较大，使得输电线与绝缘子连接两侧产生较大动张力差，增大了塔线体系的风振响应。

2）裸塔及塔线体系的风振系数均在横担处出现突变。在90°风向角下，裸塔及塔线体系横担处的风振系数均超过《110～750 kV 架空输电线路大跨越设计技术规定》中的规范值。塔线体系在90°风向角下塔顶处风振系数最大，值为2.66。

3）在90°风向角强风作用下，塔线体系在46 m/s的风速下发生倒塌。输电塔风致倒塌是由第8 节间斜材首先发生失稳，导致相邻杆件内力重分布，最终在第5 节、第6 节间塔体出现明显弯折，导致输电塔倒塌。

4）在基本风速41 m/s 下，输电塔的整体稳定性满足要求，但考虑其复杂的运行环境应结合其在强风作用下的倒塌特征，对该线路做加强设计，例如在易发生面外失稳的斜材处增设横隔面，以确保输电塔局部稳定。